关于隐函数存在定理的注记

张再云, 江五元, 丁卫平, 李松华, 方春华, 何 帆

(湖南理工学院 数学学院, 湖南 岳阳 414006)

0 引言

常微分方程是数学与应用数学、信息与计算科学专业的一门主要基础课.基于“双一流”学科建设背景下, 大学数学教学与研究需要培养创新型人才, 需要加强数学思想方法和数学创新思维能力的培养[1,2].同时, 常微分方程解的存在性唯一性定理是微分方程的重要理论基础[3].数学分析是数学与应用数学、信息与计算科学专业的一门主干核心课程, 在整个数学课程体系中占重要地位.众所周知, 隐函数存在定理是数学分析教学中的重点和难点之一.在实践教学中, “隐函数存在定理”的证明较为复杂, 学生难以接受和掌握.基于长期从事数学分析与常微分方程课程教学的经验, 本文给出数学分析中“隐函数存在定理”的一个证明, 有利于学生的理解和掌握, 达到了很好的教学效果.

关于“隐函数存在定理”的证明, 已有较多研究[12～17], 主要证明方法包括压缩映射原理[4～5]、不动点定理[6]、零点定理、压缩映射原理、多元微分中值定理[7]、微分中值定理[8]、泛函分析方法[9]、逐次逼近法[10]等, 本文利用Peano 存在性定理证明隐函数存在定理.

1 隐函数存在定理及其证明

隐函数存在定理设D是空间 ℝ ×ℝn内的一个区域, 函数F:D→ℝn;(x,y) →F(x,y)是连续可微的,而且满足条件

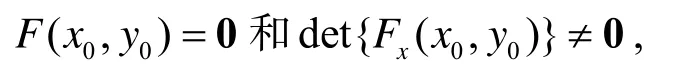
其中初值 (x0,y0)∈D, 则方程F(x,y)=0 确定一个满足条件y(x0)=y0的隐函数y=φ(x).

证明由条件 det{Fx(x0,y0)}≠0 (其中 (x0,y0)∈D)知, 存在小的矩阵区域

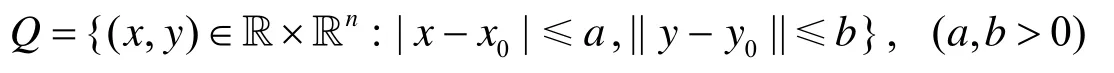
使得当(x,y)∈Q时, 矩阵Fx(x0,y0)是可逆的.因此函数

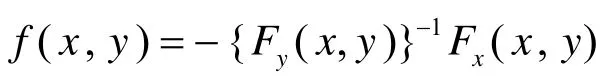
在区域Q上是连续的.根据Peano 定理知, 初值问题

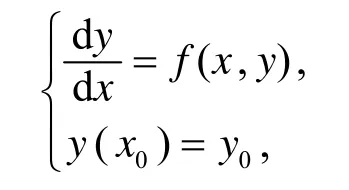
存在一个局部解y=φ(x),x∈[x0-h,x0+h](h＞ 0).从而

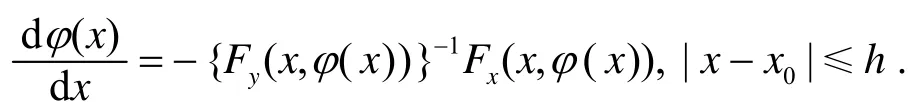
这就证明了F(x,y)=0 至少存在一个满足条件y(x0)=y0的隐函数y=φ(x).

下面再证明隐函数的唯一性.

设y=φ1(x)和y=φ2(x)都是方程F(x,y)=0 满足初始条件y(x0)=y0的隐函数, 则有

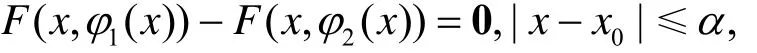
其中α＞ 0为适当下的常数.另外对向量函数F(x,y)的第i个分量Fi(x,y)应用Lagrange 中值公式, 得

其中u(x)=φ2(x) -φ1(x),u j(x)是u(x)的第j个分量, 而θi(x)满足不等式

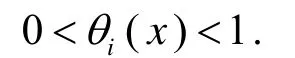
注意, 当α充分小时,φ2(x) ≈φ1(x)≈y0, 从而上述线性方程组的系数矩阵近似于Fy(x0,y0), 所以它是非退化的.因此, 上述线性方程组蕴含u(x)=0, 亦即φ2(x)=φ1(x).这就证明了唯一性.

2 结束语

隐函数存在定理是数学分析教学中的重点内容和难点内容之一, 而Peano 存在性定理是常微分方程解的存在性唯一性定理中的重要基础.本文基于常微分方程理论, 运用Peano 存在性定理证明隐函数存在定理, 证明思想与方法简单明了, 能开拓学生的研究视野, 有利于学生的理解和掌握.