二次型最优控制在小车倒立摆控制系统中的应用

彭 锦, 黄 为, 熊 欢

(湖南理工学院 信息科学与工程学院, 湖南 岳阳414006)

0 引言

对于倒立摆控制系统稳定性的研究具有非常重要的工程实践意义.任何重心在上、支点在下的控制问题, 都可以视为倒立摆系统.比如, 机器人行走过程中的平衡控制、火箭发射中的垂直度控制和卫星飞行中的姿态控制等等, 因此倒立摆的稳定控制方法在工农业生产和生活中有着广泛的应用[1,2].目前国内外学者将不同的控制方法引入倒立摆稳定性控制系统设计中.文[3]和[4]将云模型引入倒立摆控制系统设计, 抛弃了常规控制需要倒立摆确定的数学模型, 只需依据经验规则, 将人的命令通过云模型转换为控制算法, 从而实现对倒立摆的智能控制.文[5]将神经网络模型和模糊控制结合起来, 利用神经网络的运算结果修正模糊规则, 从而实现了对倒立摆的智能控制.文[6]设计了基于增强型算法的模糊神经网络控制器, 使倒立摆控制系统的稳定性得到了增强.文[7]将等效控制、切换控制和模糊控制结合起来, 形成了模糊滑模控制, 可以显著降低倒立摆稳定控制中的抖动问题.本文将线性最优控制引入二级倒立摆控制系统设计中, 对其控制性能进行研究, 为后续实际应用提供理论依据.

1 二级倒立摆控制系统的数学模型

为了简化建模的过程, 忽略两个摆杆之间的摩擦力和摆杆的空气阻力, 只考虑小车与导轨之间的摩擦力.模型简化图如图1所示, 各部件的参数含义和数据参考文[2].

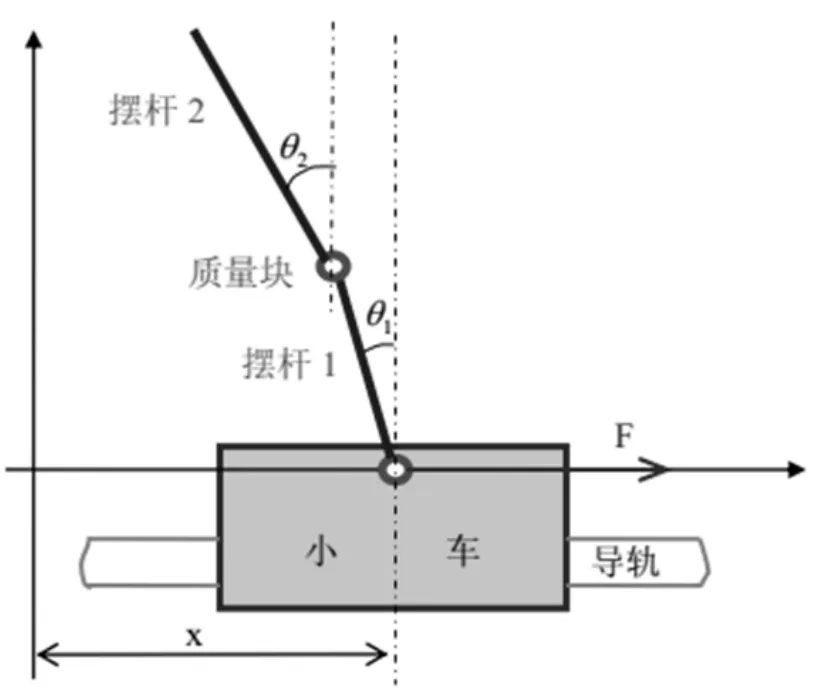
图1 二级倒立摆的简化物理模型

拉格郎日方程为

该方程用广义坐标qi可表示为

其中f i(i=1,2,3…n)为倒立摆系统沿广义坐标方向的外力.

对于该二级直线倒立摆系统, 可用拉格郎日方程推导其动力学方程.设该系统的三个广义坐标分别为x,θ1,θ2.首先计算系统的动能

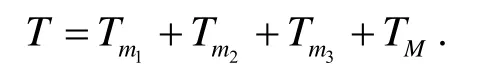
其中TM为小车的动能,Tm1为摆杆1 的动能,Tm2为摆杆2 的动能,Tm3为质量块的动能.

小车的动能

摆杆1 的动能Tm1=Tm′1+Tm′1, 其中

所以

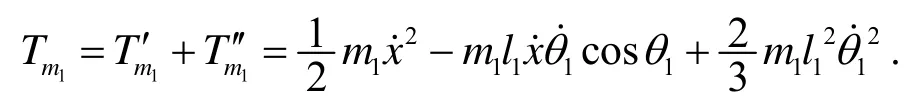
摆杆2 的动能Tm2=Tm′2+Tm′′2, 其中

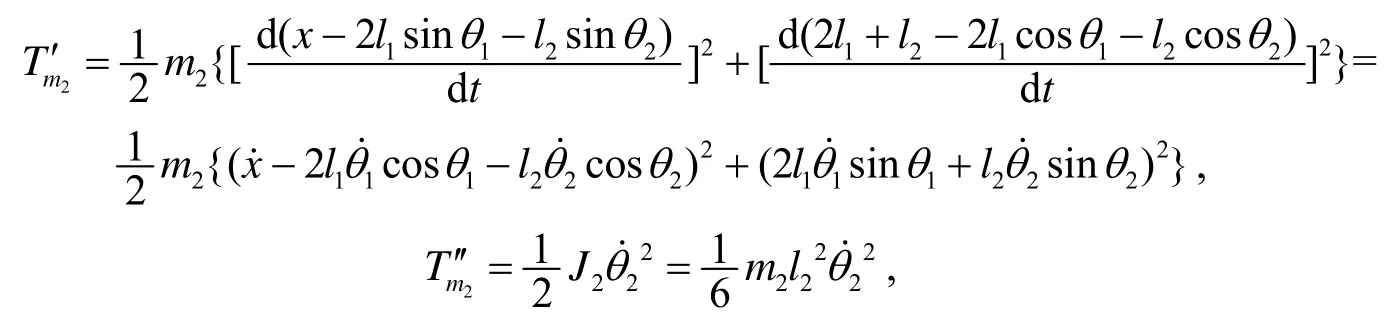
所以

质量块的动能为

所以系统的总动能为

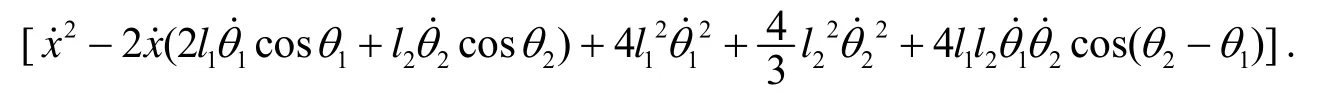
然后计算系统的势能

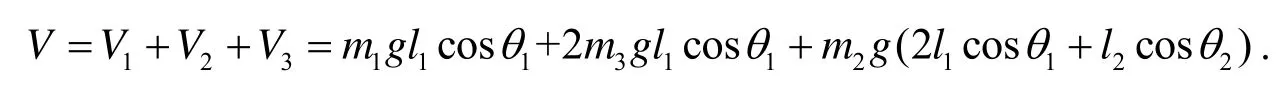
可以得出拉格朗日算子为:

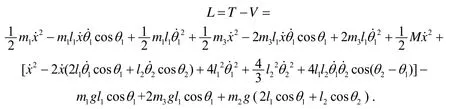
由于广义坐标θ1,θ2上无外力, 所以有

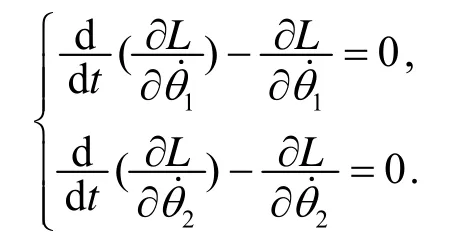
化简以上两式, 得

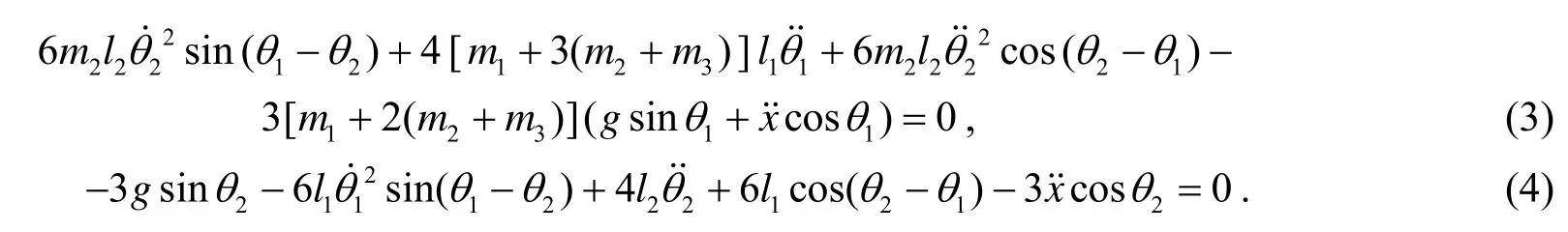
式(5), (6)可表示为

2 二级倒立摆系统的能控性和能观性分析

2.1 二级倒立摆系统的空间表达式

要使二级直线倒立摆系统在平衡位置时每个参数的初始数值全为0, 即=(0,0,0,0,0,0,0).将式(5)在平衡位置处使用泰勒级数展开并线性化, 各个参数记为

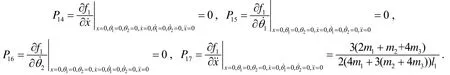
再代入到式(7)中, 得线性化之后的式子

同理, 将式(6)也在平衡位置处使用泰勒级数展开并线性化, 各个参数记为

再代入式(8)可得

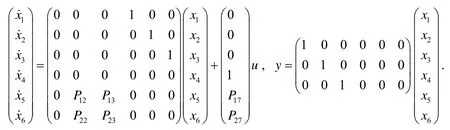
将文[2]中参数代入可得二级直线倒立摆系统的状态空间表达式为

根据稳定性的判据可知: 当系统特征方程的根全部位于左半s 平面时系统稳定.

二级倒立摆系统的特征方程为det(λ-A)=0, 通过MATLAB 求解特征根可得系统的特征根为-10.0438, 10.0438, -5.0265, 5.0265, 0, 0.

可以看出二级直线倒立摆系统的特征根不全位于左半s 平面, 因此二级直线倒立摆系统不稳定.

2.2 二级倒立摆系统的能控性和能观性分析

线性定常连续系统完全可控的充要条件是 rank(B,AB, L,An−1B)=n, 其中n为系统矩阵A的维数.由式(11)可知:

故rank(B,AB, L,A n−1B)=6, 所以系统完全可控.

线性定常连续系统完全可观测的充要条件是 rank(C,CA, L,CAn−1)T=n, 其中n为系统矩阵A的维数.由式(11)及式(12)可知

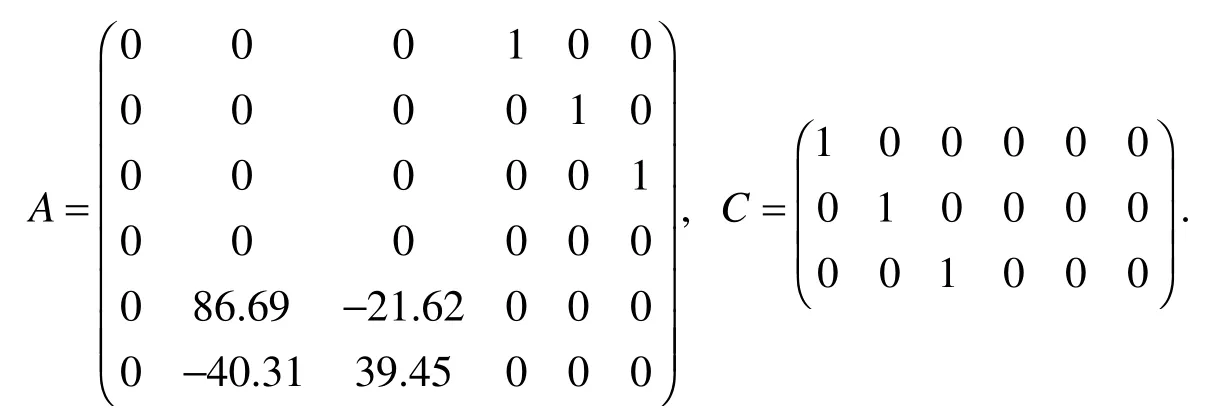
故rank(C,CA,L,CAn−1)T=6, 所以系统完全可观测.

由此, 可以确定状态反馈增益向量为

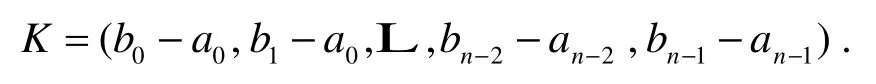
通过改变K的值去改变特征方程的系数, 从而实现对闭环极点的任意配置.

在MATLAB 中可以通过acker(A,B,J) 或place(A,B,J) 求得状态反馈增益向量K, 其中J为由n个期望极点组成的矩阵.

3 二级倒立摆控制系统的线性二次型最优控制器的设计

如果某个控制系统是一个线性系统, 那么可以对其使用线性二次型最优控制理论来进行控制.二次型性能函数是由控制变量和状态变量的二次型函数的积分构成的, 线性二次型最优控制就是利用二次型性能函数来寻找最优控制的过程.控制过程中所用的控制能量最小是使用二次型性能指标最小化的体现.也就是运用二次型的性能指标J表示系统的控制能量与控制目标间的关系, LQR 算法原理图如图2所示[8～10].

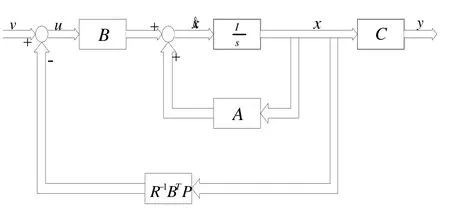
图2 LQR 算法原理图

假设给定的线性时变系统的状态空间表达式为

LQR 最优设计的关键是要设计出能使二次型目标函数J取最小值的状态反馈向量K.二次型目标函数J为

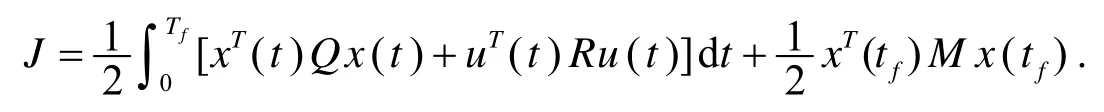
其中Q是对于状态向量的加权矩阵,R为正定矩阵.

因为要使性能指标J最小, 所以可以先使用Hamilton 函数, 即

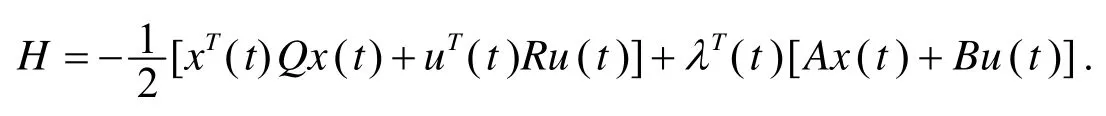
对u求取偏微分, 得

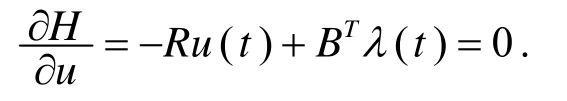
由此可以得到系统的最优控制信号为u(t)=-R-1BTP(t)x(t), 其中

当tf→∞时,P(t)趋于常数矩阵, 所以(t) →0.故式(13)可化简为

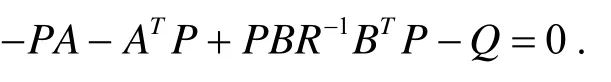
通过求解上式可以得出正定矩阵P, 又由K=R-1B TP, 可以求得最佳状态反馈矩阵K.在MATLAB中可以通过lqr(A,B,C,D,J)求得线性二次型反馈增益向量K.

4 二级倒立摆标准LQR 控制器系统的仿真研究

LQR 控制器的作用是在输入阶跃信号时, 用最小的能量、较快的速度对其作出反应, 驱动小车使摆杆1 和摆杆2 保持平衡和竖直向上的状态.当性能指标函数的值越小时, 控制的效果越好.在MATLAB 中可以通过lqr(A,B,C,D,J)求得线性二次型反馈增益向量K, 其中Q为加权矩阵, 是一个半正定的对角矩阵.对角线上的值为状态变量的加权值, 权值越大时其对应的状态变量衰减速度越快.在MATLAB 的Simulink 工具箱中进行仿真, LQR 控制的仿真模型如图3所示.

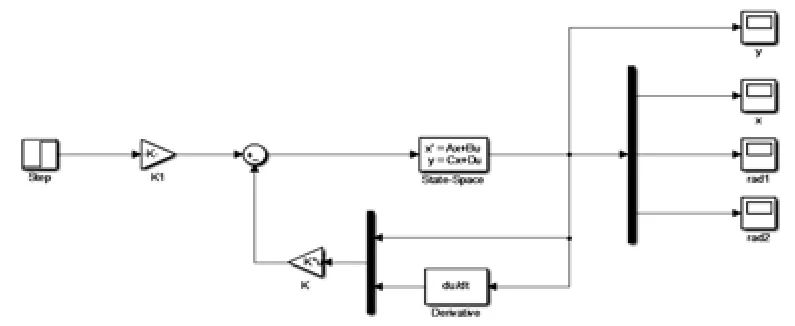
图3 LQR 控制器仿真模型图

输入的阶跃信号的幅值为0.1, 状态变量的初始值为(0, 0, 0, 0, 0, 0).下面通过试凑法来确定加权矩阵Q的值:

(1)令Q11=1,Q22=1,Q33=1,Q44=0,Q55=0,Q66=0,R=1, 可求得:K=(1.0000, 76.0260, - 82.4403, 2.0165, 4.6197, - 12.7021), 仿真结果如图4所示.

由图4可以看出, 小车位移的调节时间为7s, 上升时间为3s, 摆杆1 和摆杆2 的调节时间为6s, 系统达到稳定的时间过长, 控制效果很差, 所以继续增大Q的值.

(2)令Q11=300,Q22=1,Q33=1,Q44=0,Q55=0,Q66=0,R=1, 可求得K=(1.0000, 76.0260, - 82.4403, 2.0165, 4.6197, - 12.7021), 仿真结果如图5所示.

图4 系统阶跃仿真图

图5 系统阶跃仿真图

由图5可知, 增加了Q11的值后, 三个输出量的调节时间都降低到了4.5s 左右, 但是三个输出的超调量都增大了, 且系统的震荡比较大, 所以继续调节加权矩阵Q的值.

(3) 令Q11=300,Q22=500,Q33=500,Q44=0,Q55=0,Q66=0,R=1, 可求得:K=(17.3205, 116.5703, - 194.6000, 18.5650, 3.5456, - 31.4350), 仿真结果如图6所示.

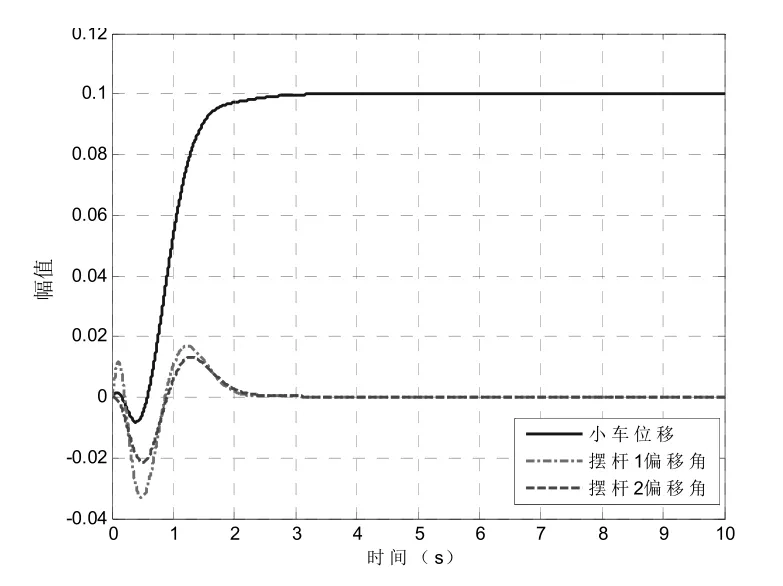
图6 系统阶跃仿真图

由图6可知, 经过调整后, 小车位移、摆杆1 和摆杆2 曲线的调节时间为2.5s, 系统的快速性比较好, 相比于图4和图5, 系统的超调量明显降低, 且震荡也减小了.摆杆1 和摆杆2的摆动幅度都比较小, 控制的效果比较理想.

为了检验系统的抗干扰能力, 在系统仿真模型中加入Pulse Generator 模块, 在5s 时产生一个脉冲干扰信号.仿真模型如图7所示.

在Q11=300,Q22=500,Q33=500,Q44=0,Q55=0,Q66=0,R=1的情况下, 仿真模型的阶跃响应如图8所示.

图7 系统仿真模型图

图8 加入扰动后的阶跃响应图

由图8可知, 在扰动的作用下, 两个摆杆的角度偏移都不大, 在短时间内都恢复了稳定状态, 所以系统具有较强的抗干扰能力和较好的鲁棒性.

5 结论

本文以二级倒立摆为实验对象, 建立了倒立摆装置的数学模型, 同时进行了线性化处理, 得到了系统的状态空间表达式, 分析了系统在阶跃输入下的响应情况.在得到状态空间表达式的基础上, 分析了其能控性与能观测性.最后将二次型最优控制引入控制系统设计中, 通过仿真结果分析得出: 二次型最优控制具有较强的干扰能力, 可以应用于要求比较高的场合.