基于PCA-SVDD 的滚动轴承性能退化评估
2020-04-17吴义岚廖爱华丁亚琦
吴义岚,廖爱华,丁亚琦
(1.上海工程技术大学 城市轨道交通学院,上海 201620;2.上海地铁维护保障有限公司车辆分公司,上海 200235)
滚动轴承作为常用的机械部件,极易损坏.调查数据显示,30%左右的旋转机械问题都是由滚动轴承的故障[1]导致的.选择合理有效地方法来反映滚动轴承在整个寿命周期内的退化程度,可实现设备的接近零停机时间和最大生产率.因此性能退化评估技术应运而生,与故障诊断相比,此技术能更有效地实现机械状态的维护.
目前,针对滚动轴承性能退化评估的问题,国内外学者提出很多方法,包括支持向量机(SVM)[2]、隐马尔科夫模型(HMM)[3]、高斯混合模型(GMM)[4]、余弦欧氏距离[5]等,但这些方法都存在各自的缺陷:采用SVM 构建的模型一般需要采集大量的数据完成模型训练,但是实践中很难获得大量设备故障的样本;HMM 通过指数分布的方式刻画各健康状态的区间长度,与实际情形并不相符;GMM在轴承并未失效时便会接近于取值上限,没有办法判断出轴承是否已经失效;余弦欧氏距离方法没有考虑到总体变异对距离远近的影响,缺乏自适应性.
支持向量数据描述(Support Vector Data Description,SVDD)最初是Tax 等[6]以边界思想为基础提出的单值分类算法,其鲁棒性好,准确性高.此外,这种算法可以只使用正常状态的样本数据完成模型的训练,较好地解决了因故障数据匮乏而无法及时发现轴承故障的问题[7−8].主成分分析法(Principal Component Analysis,PCA)能够精简相关性较强的数据造成的信息重叠,具有较好地空间映射和融合的能力,且自身较为稳定,可以有效解决滚动轴承振动信号的单一特征指标无法全面体现滚动轴承运行中退化状况的问题[9−11].基于此,采用PCA 算法对滚动轴承的时域和频域特征指标进行加权融合,将得到的综合特征指标作为SVDD 模型的输入,进行滚动轴承性能退化评估,利用Cincinnati 大学的滚动轴承全寿命试验数据进行检验.
1 性能退化评估模型
首先使用PCA 算法对滚动轴承的正常数据进行处理,时域和频域特征指标组成的矩阵表示为
式中:Xi=[xi1,xi2,···,xin]Ti为第 个相对特征指标的序列.
对原始矩阵进行零均值处理,通过线性变换得到新的坐标系Y1,Y2,···,Yp,将X的协方差矩阵的特征值 λ 由大到小排列,通过线性组合得到第1,第2 至第p个主成分.将第1 主成分作为衰退性能指标,用于滚动轴承的性能退化评估,得到公式

然后将PCA 处理后的训练数据输入SVDD 模型进行训练建模.SVDD 原理是找出涵盖目标类对象的最优超球体,主要思想是将目标类对象看作一个整体,然后模拟出密封且紧密的超球体区域,让目标对象绝大部分都处于超球体的范围中,那些非目标对象绝大多数都被隔离在超球体之外[6].SVDD 超球体原理如图1 所示.
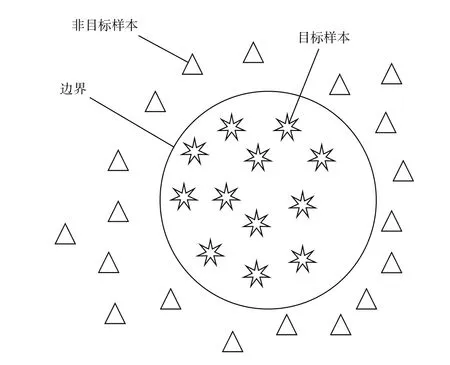
图1 SVDD 二维空间原理图Fig.1 Schematic diagram of SVDD two-dimensional space
观察图1 可以看出,如果目标对象存在野点,大概率会产生一个很大的超球体,这类情况导致目标样本区域不能很好地被描述.通常把增强样本分类稳定性的惩罚因子添加到SVDD 中,实现算法复杂度与错分样本比例之间的折中.同时,样本原始的特征空间边界一般不够紧密,导致不能有效地对样本数据进行表征.因此,采用支持向量机的相关理论,利用核函数取代内积运算,即
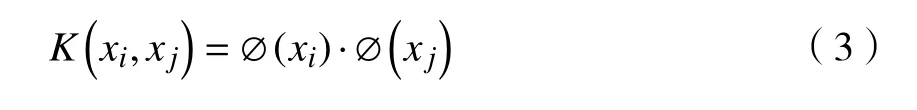
从而把低维度的非线性问题转换成高维度的线性问题完成计算.因为高斯核函数可以处理原特征数据过度上涨的情况,所以在SVDD 中引入此核函数.假定超球体中心是为O,半径为R,R可通过公式求得,公式为

式中:xs为支持向量;αi为Lagrange 乘子;xi为目标对象;下标i,j为目标样本数据.将待测数据z进行特征提取,得到其特征矢量xz作为新样本,新样本距离超球体中心点O的广义距离D为

若D≤R,则待测数据z和训练数据属于同类;反之,则非同类,视作非正常点.
通过计算D与R的差值,能够评估待测数据z与训练数据的差值,差值与偏离程度成正比.根据此原理,即可用SVDD 模型来判断滚动轴承的性能退化情况.
2 性能退化评估方法
2.1 性能退化评估流程
滚动轴承的性能由于使用时间的增长而逐渐降低,借助SVDD 能够完成对偏离程度的整体评估.通过PCA-SVDD 可实现滚动轴承性能退化的评估,详细流程如图2 所示.

图2 性能退化评估流程Fig.2 Evaluation process of performance degradation
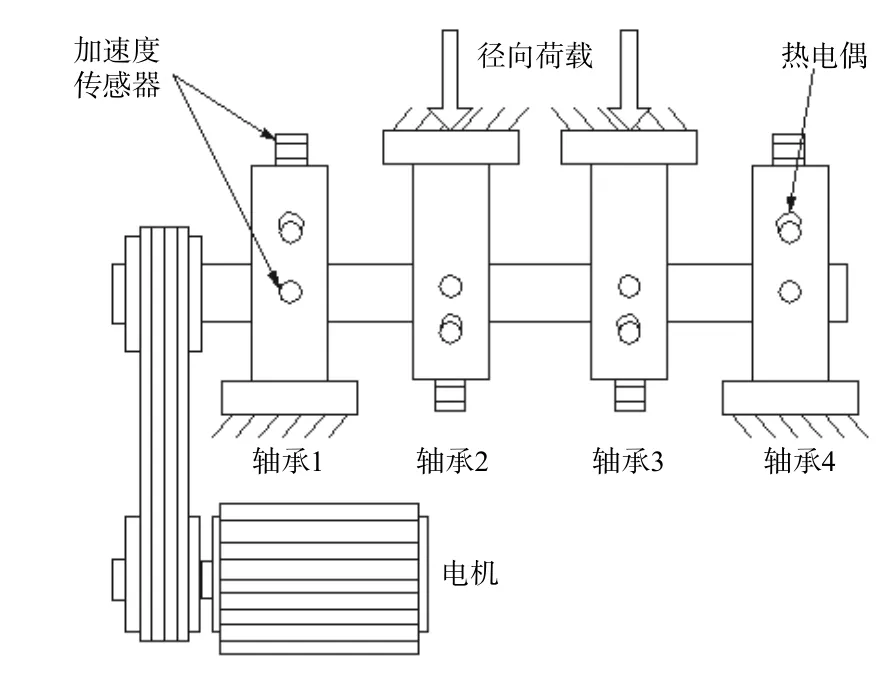
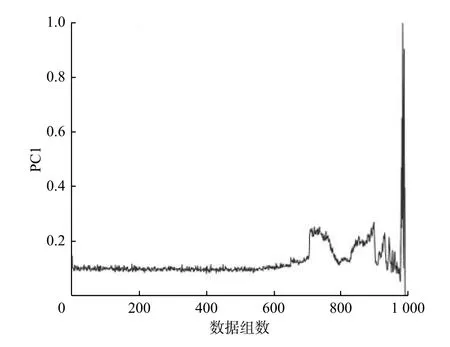
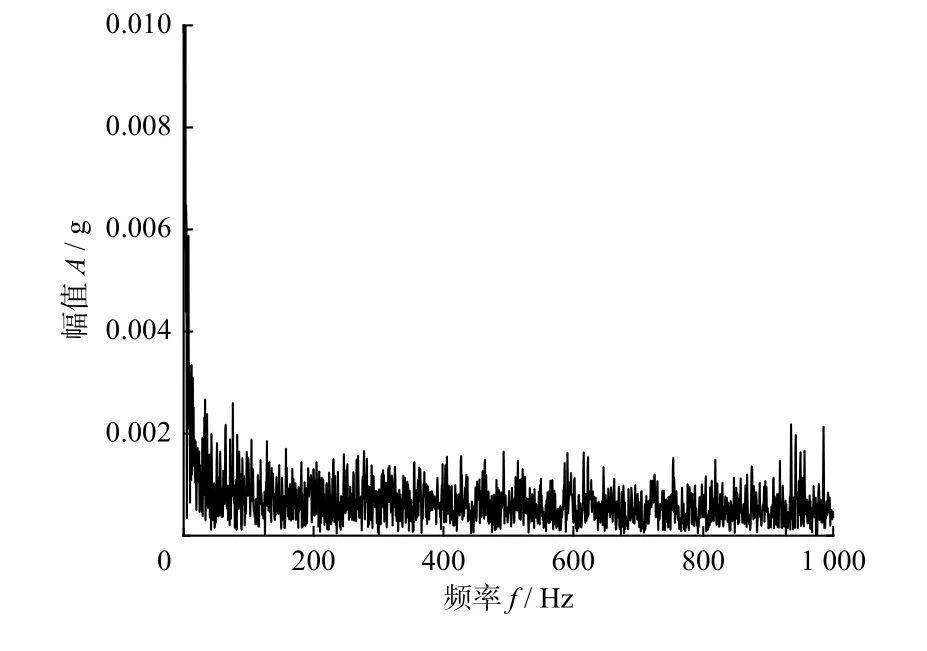
主要步骤为:1)采集正常状态下样本的时域及频域特征指标,借助PCA 方法完成加权融合,获取融合特征指标;2)把步骤1)中获取的正常状态下的样本特征向量看作训练数据,搭建SVDD 模型,进一步获取SVDD 超球体,通过式(4)计算超球体半径R;3)对待测信号利用PCA 算法进行处理,输入到训练完毕的SVDD 模型中,借助式(5)求解得到与超球体中心的广义距离D,以此作为轴承性能退化评估的评判指标,并通过健康报警阈值来监测轴承的早期退化.当D D是一个连续变化的量,表示设备偏离正常状态的程度.设定报警阈值有利于实现对轴承工作情况的实时监测.目前阈值设置还没有统一的标准,常用阈值设置方法有两种:Wang 等[12]将SVDD训练模型的超球体半径R设为阈值;Lin等[13]根据统计学中的3σ法则,将µ+3σ 作为阈值,其中:µ为均值;σ为标准偏差.本文使用这两种方法进行阈值设置并比较其效果. 采用Cincinnati 大学的滚动轴承全寿命试验数据检验方法的有效性,滚动轴承测试装置如图3所示. 图3 滚动轴承测试装置Fig.3 Testing device of rolling bearing 测试装置中电机带动主轴进行运动,转速为2 000 r/min,滚子直径为8.407 mm,节圆直径为71.501 mm,接触角为15.17°.每10 min 对轴承振动信号进行一次采集.工作163 h后,轴承2 因为产生严重的外圈故障而失效.本文采用轴承2 收集到的全寿命样本(共984 组)作为试验的数据.根据相关文献[14],在500 点前,滚动轴承均可以正常运行.因此,选取500 组之前的数据作为正常样本训练SVDD 模型. 3.2.1 不同阈值的评估结果 通过PCA 将时域指标和频域指标进行融合,提取出第一主成分(PC1)作为综合特征指标,提取的第一主成分如图4 所示. 构建好PC1 性能退化指标后,将状态正常的前500 组数据作为评估试验的正常样本,对SVDD模型进行训练,获得SVDD 超球体后,把984 数据当作待测样本,按照2.1 节的评估方法输入到SVDD模型中,得到轴承全生命周期的D值.为进一步降低外界因素对D值所造成的影响,对其进行五点平滑处理.所得结果如图5 和图6 所示,从图中可以看出,以SVDD 超球体半径设置阈值,在5 740 min(数据组数为574,每隔10 min 采集一组)报警,以3σ法则设置阈值,在5 960 min 报警.故将SVDD模型超球体半径R设为阈值能够更早的发现故障点. 图4 PCA 约减融合后的特征指标Fig.4 PCA reduced feature indicators after fusion 另外,由图5 可知,轴承在5 740 min 达到阈值线,表明开始出现轻微故障.在6 890 min后,D值出现剧烈增长,表明滚动轴承处于故障发展阶段,9 650 min后,D值没有明显增加,说明滚动轴承正在向失效发展.在6 890~9 650 min 中D值先增大后减小再上升,这种波动趋势可以用损伤传播过程的性质来解释.当表面缺陷刚萌生时,会形成小的剥落或裂纹,随后通过连续滚动接触使其光滑.随着损伤扩展到更广的区域,振动水平再次升高[15].综上所述,该轴承的性能退化可以分为4 个阶段:0~5 740 min为正常阶段;5 740~6 890 min为轻微故障阶段;6 890~9 650 min为故障发展阶段;>9 650 min为轴承失效阶段. 图5 以R为阈值时PCA-SVDD 模型性能退化评估结果Fig.5 Performance degradation evaluation results of PCASVDD model with R as the threshold 图6 按 3σ法则设置阈值时PCA-SVDD 模型性能退化评估结果Fig.6 Performance degradation assessment results of PCA-SVDD model when threshold is set according to 3 σ rule 3.2.2 均方根值和峭度为指标的评估结果 振动信号的关键评价指标有均方根值、峭度等.轴承出现磨损类问题通常通过均方根进行判断比较合理,轴承磨损越严重,则均方根值越高;在轴承工作期间,轴承的最初阶段峭度指标更加灵敏,一旦轴承在初期产生轻微故障,峭度值相比均方根值的反映更灵敏[16].使用这两个指标作为特征指标分别输入SVDD 模型中进行训练和测试,同样采用五点平滑的方式对结果进行处理,得到结果如图7 和图8 所示.图7 中峭度指标结果在前5 000 min 就出现多次大的波动,影响判断,不适合作为SVDD 模型的特征指标.图8 中均方根值结果在6 060 min 出现故障,相比PCA-SVDD 方法的结果推迟了320 min,不能及时发现故障. 图7 峭度为特征指标的性能退化评估结果Fig.7 Performance degradation evaluation result with kurtosis index as characteristic index 图8 均方根值为特征指标的性能退化评估结果Fig.8 Performance degradation evaluation results with root mean square value as characteristic index 在轴承的加速疲劳试验中,根据润滑油中金属碎屑的数量确定轴承最终失效时间,但试验时仍无法判断轴承的早期故障是出现在哪个时间点.根据模型求出在5 740 min 时,轴承便已显示出早期故障.但该结论的可靠性还需要更多的验证.参考包络知识,如果轴承本身出现故障,其包络谱在故障频率、倍频范围内会产生幅值衰减的离散谱线[17].因此,本文结合经验模态分解以及Hilbert包络解调法,对轴承振动信号的包络谱求解,以验证判断结果的合理性.文献[16]已给出上述两种方法的详细步骤,首先对不同零件相应的理论故障频率求解,结合3.1 节已知的轴承尺寸,再参照文献[18]列举的计算式,得到外圈故障频率fo=236.4 Hz,轴承内圈及滚动体故障频率分别为fi=296.9 Hz,fb=139.9 Hz,保持架故障频率fc=14.4 Hz.第200组、第574 组数据的幅值(A)和频率(f)分布包络谱如图9 和图10 所示.从图9 中可以看出,包络谱中没有出现与轴承故障频率基本一致的频率部分,同时它的幅值也不是很大.分析可知在该时段内,轴承一直是正常状态.从图10 中可以看出,第574组数据的包络谱中出现了与轴承外环故障频率fo=230 Hz 相同的频率成分230 Hz,还出现了230 Hz 谱线的倍频成分(461 Hz 和691 Hz),同时还存在很多其他的频率成分且幅值很小,说明此时的故障还比较微弱.由此可知,轴承在第5 740 min 出现了早期外圈故障,验证了模型对滚动轴承早期微弱故障预警的准确性. 图9 第200 组数据的包络谱Fig.9 Envelope spectrum of the 200th group data 图10 第574 组数据的包络谱Fig.10 Envelope spectrum of the 574th group data 提出一种基于PCA-SVDD 的滚动轴承性能退化评估方法,通过PCA 算法对滚动轴承振动数据特征指标进行加权融合,得到融合特征指标,再输入SVDD 模型得到性能退化评估的评判指标.试验结果显示,该方法可以对轴承初期产生的问题发出较为精确的警报,和采用单一指标的方法相比,能更加准确地反映轴承的实时运行情况和轴承的退化程度,以便更早地发现故障.2.2 健康报警阈值的设置
3 试验验证
3.1 试验说明
3.2 试验结果分析
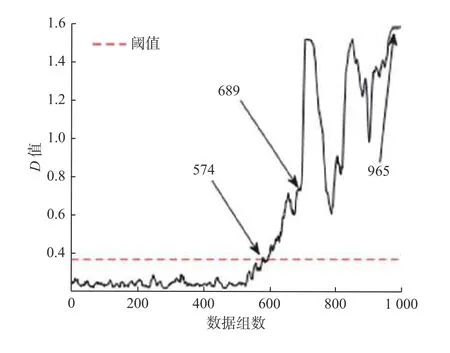
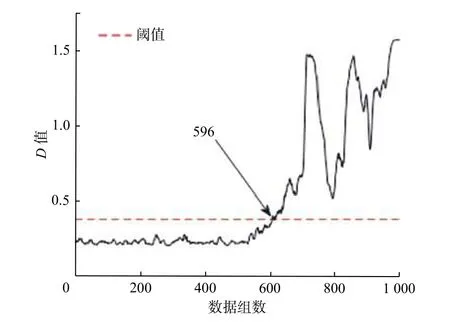
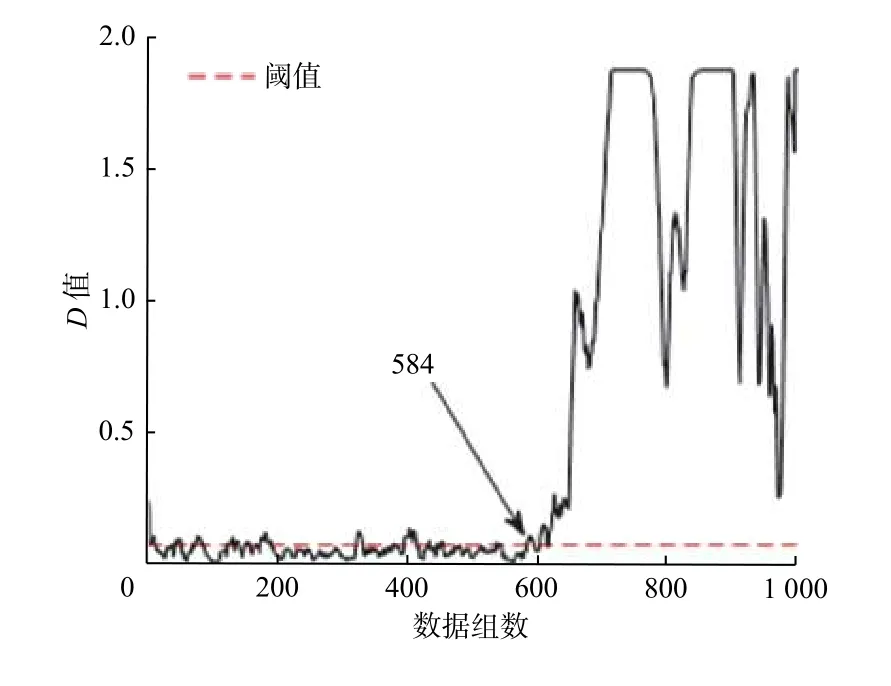
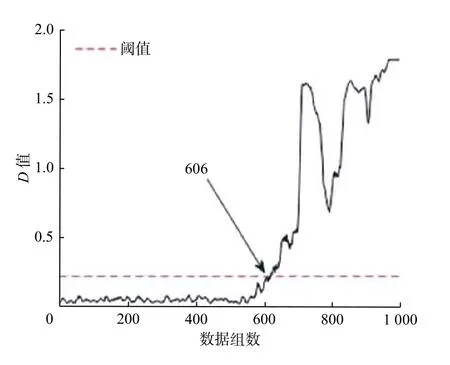
4 评估结果验证

5 结语
