基于杂交基本解的正交各向异性材料热传导问题有限元法
2020-04-17仇文凯王克用
仇文凯,王克用
(上海工程技术大学 机械与汽车工程学院,上海 201620)
材料按照性质和内部结构,一般可分为各向同性材料和各向异性材料.各向同性材料具有简单、优良的特性,在材料工程领域得到广泛的应用[1−3].Wang 等[1]采用基于杂交基本解的有限元方法(HFS-FEM)研究各向同性材料的热传导问题.Gao[2]提出一种求解各向同性材料热传导问题的无网格边界元方法.目前,在汽车、造船、机械加工、航空航天、军工等工程领域中,许多各向同性材料还不能满足性能需求,因此,研究各向异性材料仍具有重要的理论和实际意义.
在热传导问题[4−5]中,各向异性材料可分为一般各向异性材料和正交各向异性材料[6−9].各向异性材料的导热系数在各个方向上是不同的:一般各向异性材料导热系数张量中的所有元素都不为零,而正交各向异性材料导热系数张量中只有主对角线上的元素不为零.根据导热系数的不同形式,正交各向异性材料可以进一步细分为常系数或变系数两种情况.目前,关于用边界元法研究正交各向异性热传导问题的报道有很多.Perez等[10]研究一般积分方程公式并用于求解均匀正交各向异性位势问题.Divo 等[11]推导正交各向异性问题基本解的形式.Zhou 等[12]针对二维正交各向异性位势问题,建立一个新的势导数边界积分方程,称为自然边界积分方程(NBIE).通过边界元法以及其他数值方法分析此类问题已经开展了许多工作,而利用杂交基本解有限元法分析正交各向异性热传导问题的报道却非常少.
杂交基本解有限元法是基于杂交Trefftz 法的一种高效数值方法.Trefftz 方法是由Trefftz 于1926年提出的,利用满足控制方程的叠加函数来求解边值问题.随后,Jirousek 等[13]于1977 年提出杂交Trefftz 有限元法,将边界概念推广到单元间边界,并在单元内部构造满足非齐次Lagrange 方程的坐标函数.目前,杂交Trefftz 有限元法已成功地应用于许多工程问题,如位势问题[14−15]、平面弹性问题[16]、夹杂分析[17−18]、接触问题[19]、轴对称问题[20−21]等.Wang 等[22]采用杂交Trefftz 有限元法(HT-FEM),以T-完备函数作为内部插值函数,研究轴对称位势问题.Wang 等[23]基于完备解系提出分析正交各向异性位势问题的杂交Trefftz有限元模型.王克用等[24]利用杂交完备解有限元法分析功能梯度材料位势问题.刘博等[25]利用含有特解的Poisson 方程分析杂交Trefftz 有限元法的轴对称问题.杂交基本解有限元法的原始思想由Kompiš等[26]提出,其利用基本解近似位移场和应力场,并利用网线函数来实现相邻单元之间的连接.高可乐等[27]采用杂交基本解有限元法分析考虑体力项的轴对称弹性问题,与杂交Trefftz完备解有限元法相比,该方法可避免T-完备函数项选取困难,直接利用基本解来构造满足控制微分方程的单元内部插值函数.此外,与边界元法相比,该方法消除了积分奇异性的缺点,在网格畸变方面表现出良好性能[28].
本文基于文献[10−12,23]的研究工作,利用杂交基本解有限元法分析正交各向异性材料的热传导问题.
1 问题描述及基本方程

式(2)即为二维正交各向异性热传导问题的控制方程.考虑Dirichlet 和Neumann两类边界条件,为
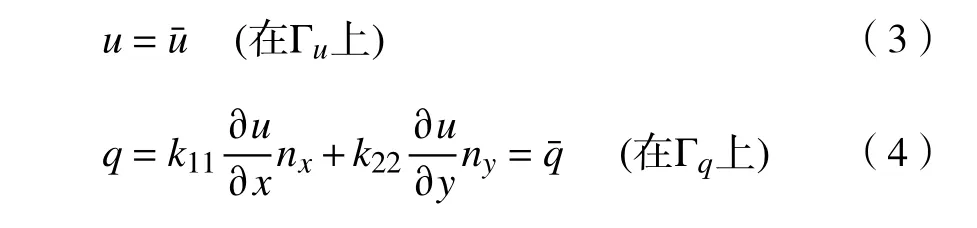
2 假定温度场
与杂交Trefftz 有限元法类似,杂交基本解有限元法采用两套假定的温度场来建立有限元模型,包括非协调单元内部温度场和辅助协调网线场.精确满足控制方程的单元内部温度场,可保证单元内各点的计算精度,而相邻单元之间则由独立定义在单元边界上的辅助协调网线场连接,与杂交Trefftz 有限元法不同的是,单元内部温度场由已知的基本解而不是T-完备函数构造.
2.1 非协调单元内部温度场
对于正交各向异性热传导问题,非协调的单元内部温度场可以表示为
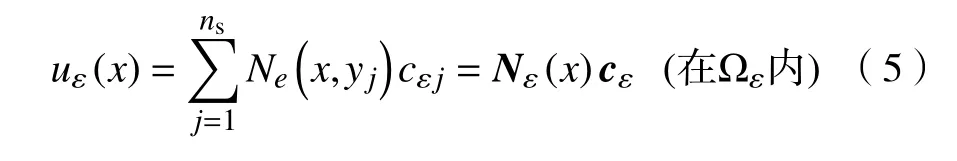
式中(:n)s为每个单元的源点个数;cej为待定参数;为二维正交各向异性热传导问题的基本解;Ωe为边界 Γe包围的单元域.问题的基本解[10−12]应完全满足方程

采用以下关系确定源点的布局,为

式中:xc为单元形心;xb为单元边界上的点;λ为无量纲参数.特殊单元的源点分布如图1 所示.

图1 两个假定温度场及其源点Fig.1 Two assumed temperature fields with source points
2.2 辅助协调网线温度场
为保证相邻2 个单元之间的连续性,在单元边界上建立一个辅助协调的网线温度场,为

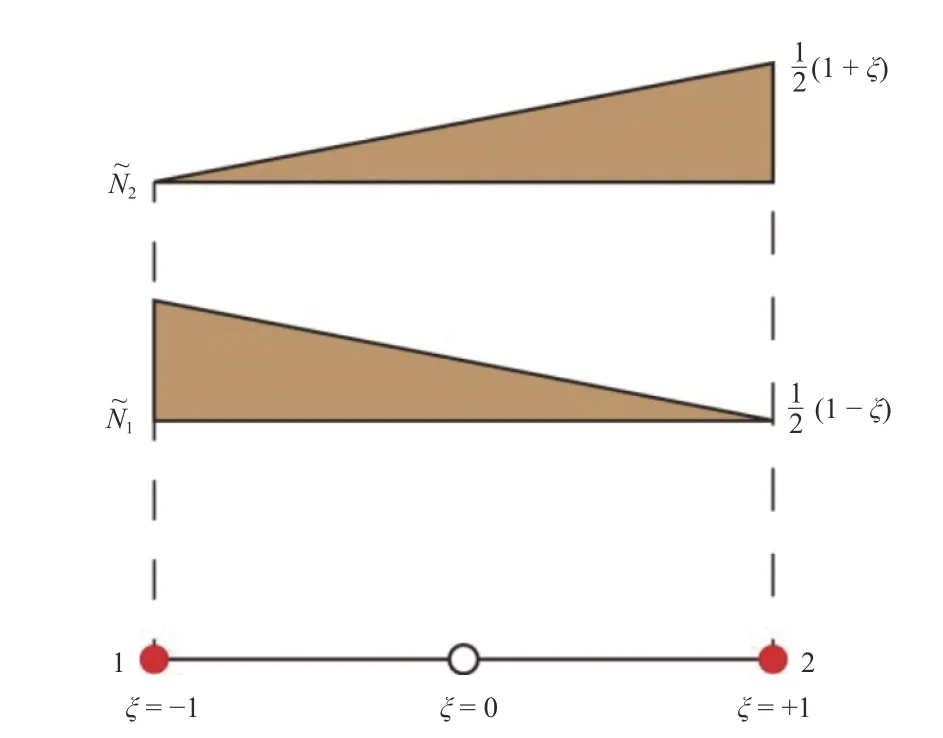
图2 两节点单元边上的形函数Fig.2 Shape functions on each two-node side of an element
沿单元每两节点边上的温度分布为


相应地,热流可表示为
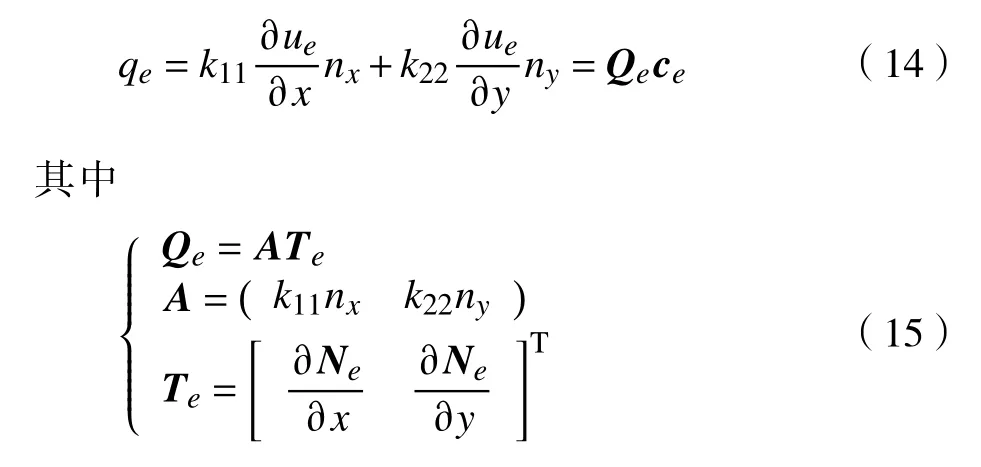
3 杂交基本解有限元列式
3.1 修正的变分泛函

3.2 刚体运动的恢复
为保证矩阵满秩,在计算单元内部场变量时,需要恢复舍弃的刚体运动项.为获得单元内任意点的真实温度,根据现有研究[1,18−19]提出的方法,可以很容易地恢复单元内温度场中舍弃的刚体运动项.因此,温度的最终表达式为

式中:m为单元节点数.
4 数值算例
为定量理解计算精度,对任意变量f 引入相对误差(ε),可得
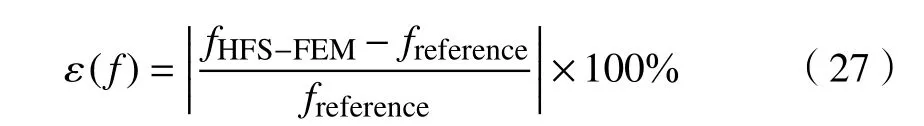
式中:fHFS−FEM和freference分别为杂交基本解有限元解和参考解.
为方便表达,算例中所有参数都采用无量纲(没有单位的物理量)的形式表示.
4.1 方形区域内的热传导
在第1 个算例中,考虑边长为0.1 的正方形区域,其中材料的导热系数为k11=1和k22=2.对正方形区域左右边界分别施加温度u=0和u=10;上部边界施加热流q=10,下部边界假设为绝热;将整个模型划分为16 个四节点四边形单元进行求解计算,如图3 所示.
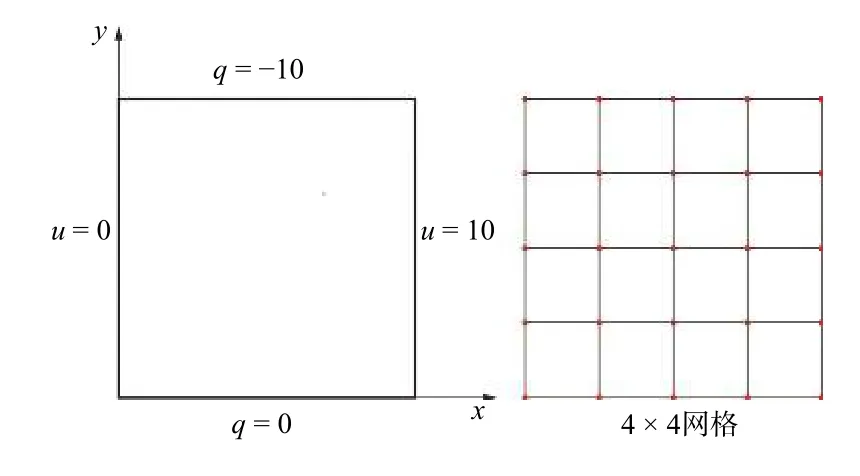
图3 正方形区域、边界条件和有限元网格Fig.3 Square domain,boundary conditions and finite element mesh
为验证杂交基本解有限元法对网格畸变的不敏感性,定义5 种网格变形方案,畸变参数 γ(=e/l)分别为0.1、0.3、0.5、0.7 和0.9,与规则网格(γ=0,不变形)的计算结果对比如图4 所示.温度u 和热流分量qx的相对误差如图5 所示.从图4中可以看出,即使对于γ=0.9 的极度扭曲网格,ε(u)的最大值仍低于0.6%,且ε(qx)低于3%,这在工程实践中是可以接受的.不同畸变程度下相同点的温度结果见表1.
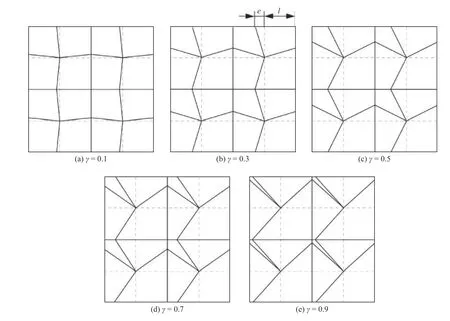
图4 网格畸变方案Fig.4 Mesh distortion schemes
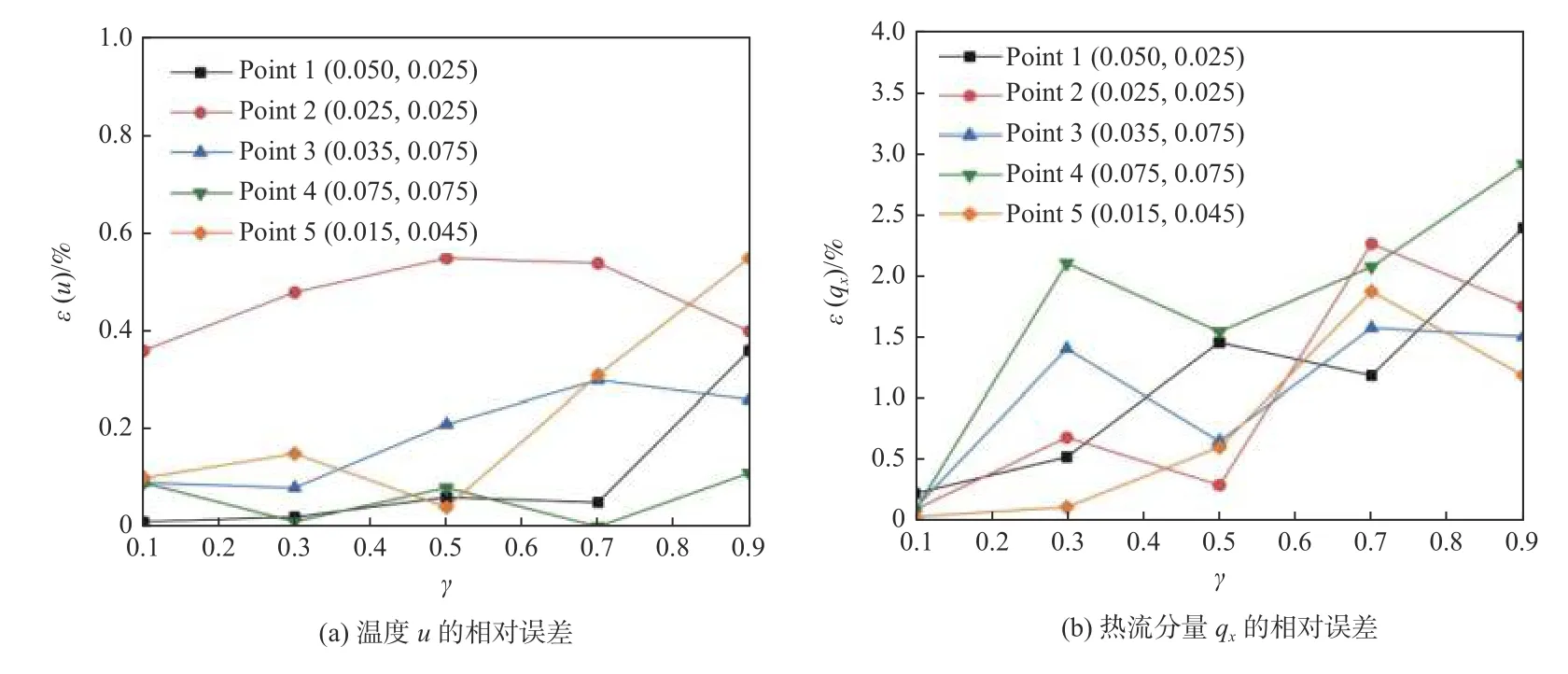
图5 温度u 和热流分量 qx的相对误差Fig.5 Relative errors of temperature u and heat flux component qx
综上表明,该方法具有对网格畸变不敏感的优点.将利用有限元软件ABAQUS 在划分841 个单元网格时的计算结果作为参考解,杂交基本解有限元法在16 个单元网格下的计算结果与之对比,两者能够较好地吻合,如图6 所示.
4.2 带圆孔的三角陀螺区域内的热传导
在此算例中,研究包含圆孔的三角陀螺域的热传导,如图7 所示.模型中,圆孔半径0.1,小弧半径0.1,大弧半径0.4.外边界上给定温度为u=20,内边界上给定温度为u=0.考虑两种网格划分,分别包含147 和1 960 个四节点四边形单元.材料的导热系数为k11=1和k22=3.三角陀螺域的温度云图如图8 所示.在粗网格下(含147 个单元),杂交基本解有限元计算结果与ABAQUS 计算结果相差不大.而与1 960 个单元下的ABAQUS 计算结果相比,该方法可以在不牺牲精度的前提下,用粗网格(147 个单元)计算出几乎相同的结果,这表明了该方法的有效性.

表1 不同网格畸变下选定5 个点的温度结果Table 1 Results of temperatures at selected five points under different mesh distortions
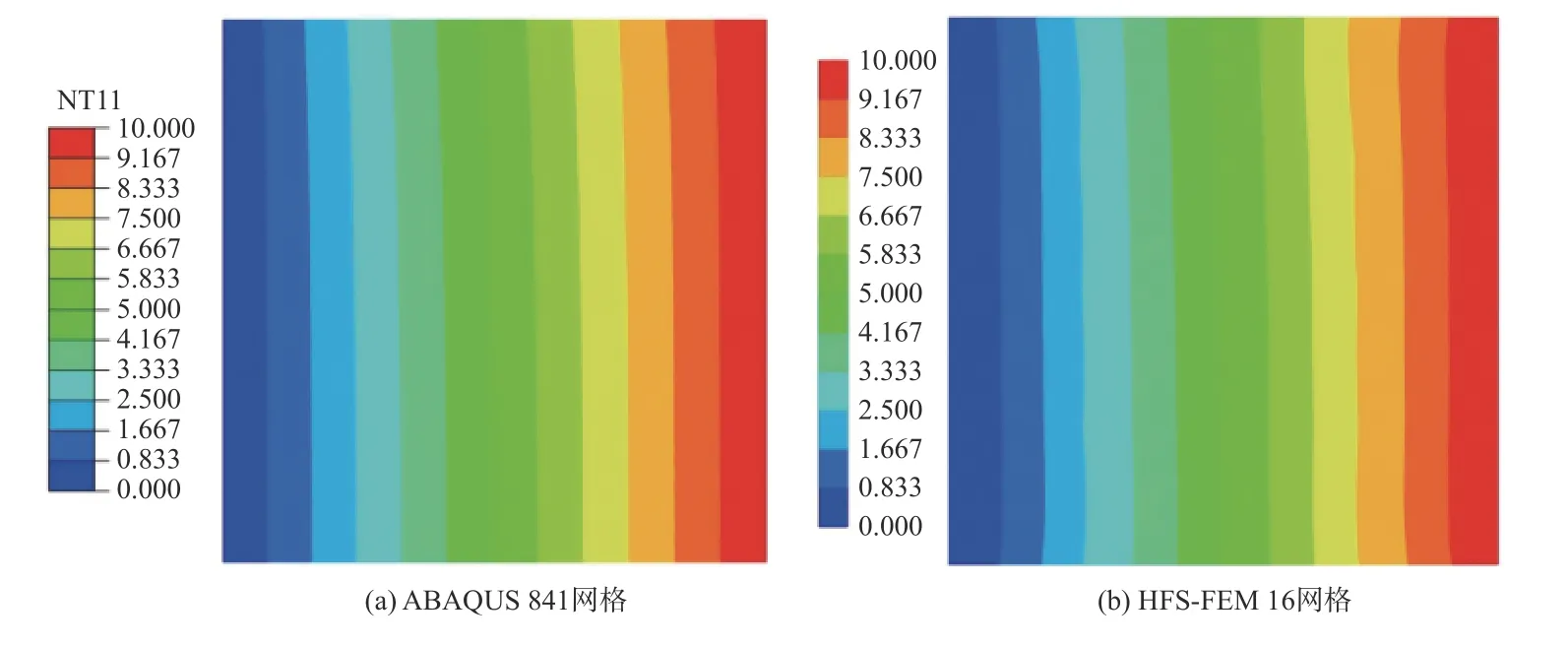
图6 方形区域温度云图Fig.6 Cloud maps of temperature in square domain
热流分量qx和qy云图分别如图9 和图10 所示.结果表明,用147 个单元的杂交基本解有限元计算结果与用1 960 个单元的ABAQUS 解更接近.对比表明,在相同条件下杂交基本解有限元法表现出更好的性能.
5 结语
本文利用基于杂交基本解有限元法研究正交各向异性介质中的热传导问题.该方法采用基本解的线性组合来近似单元域内的温度场,并引入定义在单元边界上的网线场来保证单元间的连续性.借鉴文献[10−12]的工作,构建正交各向异性热传导问题的基本解,通过修正变分泛函,将两个假定的温度场关联起来,并利用高斯散度定理和驻值定理,从而导得单元刚度方程.该方法在处理一些工程问题和物理问题时,由于其高效灵活的特点受到广泛关注和应用.数值算例表明,该方法具有计算精度高,对网格畸变不敏感且收敛速度快的优势.虽然该方法解决了稳态正交各向异性热传导问题,但是仍然可以方便地推广至瞬态情形.
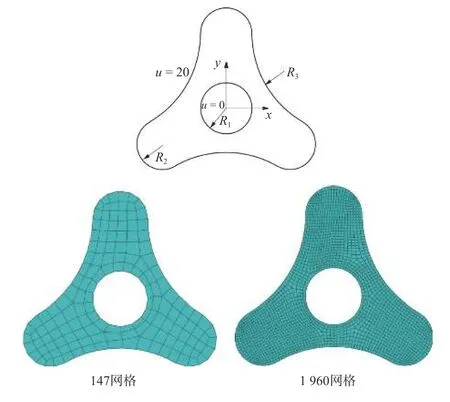
图7 三角陀螺域,边界条件及有限元网格Fig.7 Trigonometric gyroscopic domain,boundary conditions and finite element mesh
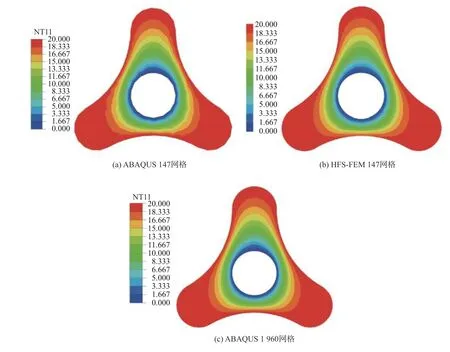
图8 三角陀螺域温度云图Fig.8 Cloud maps of temperature in the trigonometric gyroscopic domain
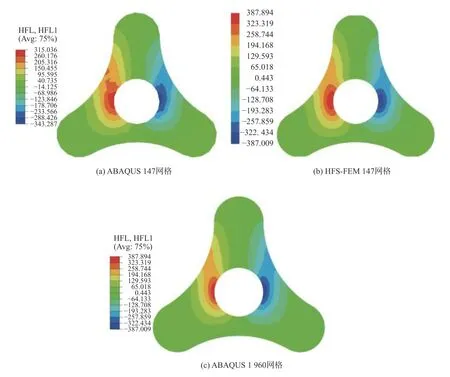
图9 三角陀螺域热流分量qx 云图Fig.9 Cloud maps of heat flux component qx in the trigonometric gyroscopic domain
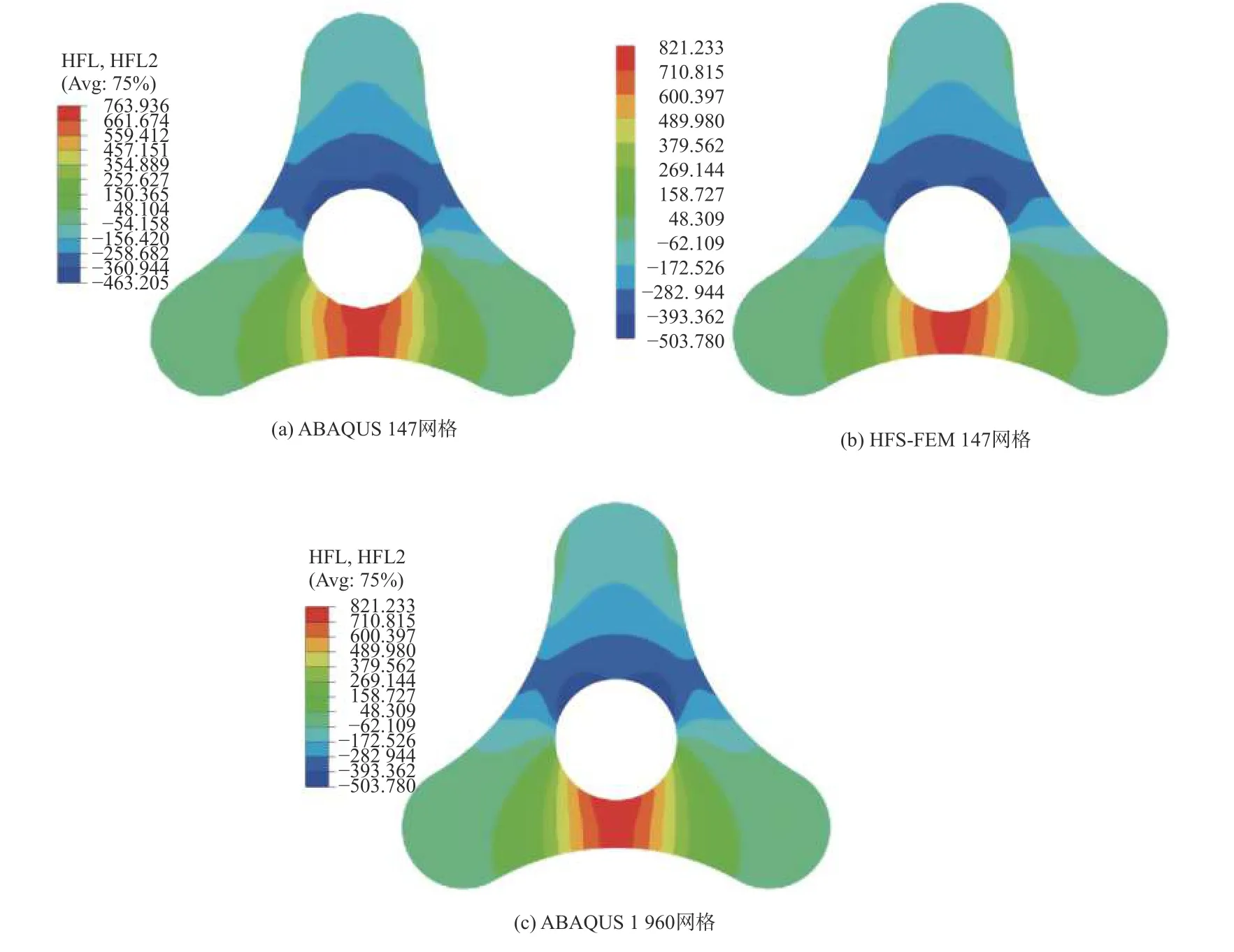
图10 三角陀螺域热流分量qy 云图Fig.10 Cloud maps of heat flux component qy in trigonometric gyroscopic domain
