原子气室内自旋极化率的空间操控与测量
2020-04-17董海峰陈静铃
董海峰,陈静铃,刘 晨,郭 军
(北京航空航天大学仪器科学与光电工程学院,北京100191)
0 引言
原子气室是原子磁强计、原子陀螺和原子钟等器件的核心敏感部件,这些器件借助原子气室内的电子自旋或核子自旋进行磁场、角速度或时间的测量。自旋方向通常情况下呈无规则随机分布,因此一般需要首先对自旋进行极化,极化的大小和方向用自旋极化率矢量来表征。气室总磁矩和总角动量与自旋极化率的关系如下

式(1)中,Mm和Ma分别为总磁矩和总角动量,μ′为电子或核子的磁矩,ћ′为电子或核子的自旋角动量,N为原子数,P为自旋极化率。在原子数确定的情况下,总磁矩和总角动量完全由自旋极化率决定,自旋极化率矢量在磁场下的演化也就代表了自旋磁矩和自旋角动量的演化。以此为出发点,便可以得到唯象的自旋动力学方程,即常用的 Bloch 方程[1]。
以上的模型中的假设是基于原子气室内的自旋极化率在空间均匀分布,或者只关心其平均值。而实际原子气室内的自旋极化率在空间有非均匀分布,对自旋极化率空间分布进行操控与测量,除了作为一种基础实验手段外,还具有应用价值,包括:1)优化自旋交换抽运效果,这对于医用核磁共振装置和核磁共振陀螺具有意义。2)通过测量自旋极化率空间分布,可获得磁场的空间分布。与磁传感器阵列测量方法相比,这种方法具有更高的空间分辨率。3)用于原子气室镀膜抗弛豫特性的微观表征。原子气室镀膜是原子自旋器件的关键技术,虽然目前有多种方法对镀膜的表面特性进行表征,但是缺乏对镀膜抗弛豫特性的微观表征手段。通过对自旋极化率空间分布的操控与测量,有望实现镀膜抗弛豫特性的微观表征。4)对原子气室内自旋极化率的空间操控,可以用于补偿极化率空间分布的不均匀。5)自旋极化率的空间操控也使得空间调制/解调成为可能,这有助于测量精度的提高。
原子气室内自旋极化率的空间操控与测量方法最早可见于1997年美国Princeton大学Happer小组的研究,该小组采用光场进行自旋极化率空间操控,采用磁共振成像进行自旋极化率空间分布测量,即光操控/磁测量方法。之后,日本Kyoto大学、德国Stuttgart大学、美国 Los Alamos国家实验室和瑞士Fribourg大学等单位也采用类似的方法进行了原子气室内自旋极化率的测量。2003年,美国Princeton大学的Romalis小组研究了磁场自旋极化率空间操控、光场分割自旋极化率空间测量的方法,即磁操控/光测量方法。之后,以色列Ben-Gurion大学、日本Kyoto大学、美国Sandia国家实验室、美国Los Alamos国家实验室和复旦大学等单位也开展过类似的研究。2019年,笔者所在的研究小组提出了基于数字微镜的光场时空双重调制原子自旋极化率空间操控方法,以及光场正交隔离自旋极化率空间测量方法,即光操控/光测量方法。以下分别对这三类研究进行详细介绍。
1 光操控/磁测量方法
光操控/磁测量方法利用光强自身的不均匀性或特制掩模板,操控自旋极化率在空间的分布,然后通过磁共振成像(Magnetic Resonance Imaging,MRI)的方法进行自旋极化率空间分布的测量。
美国Princeton大学的Happer小组先后发表过两篇利用磁共振成像进行自旋极化率空间分布测量的论文[2-3],其研究动机主要是优化医用电子-核子自旋交换抽运系统。光操控/磁测量方法的基本原理和测试结果如图1所示[2]。
其中,图1(a)为实验原理图,Zeeman共振对应自旋极化率横向x方向的分量即为图1(b)测试结果中的自旋极化率信号。该方法与核磁共振成像的方法类似,采用磁场梯度进行空间位置的编码,不同的磁场大小对应不同的空间位置。给定射频场的频率,输出共振信号为


图1 美国Princeton大学的光操控/磁测量方法Fig.1 Optical manipulation/magnetic measurement method developed by Princeton University

式(2)中,G为磁场梯度,γ为旋磁比,扫描射频场的频率为w,磁场为B。输出信号的大小主要取决于共振峰附近的极化率,即附近的极化率Pz(x),其空间分辨率可以用来表征。理论上,可以通过增大G的方法来无限提高空间分辨率,但是由于扩散的影响,G对Δx的影响会趋近于饱和,其临界梯度为(其中,D为扩散系数,T2为横向弛豫时间)。考虑到Δw=其对应的空间分辨率为
美国Princeton大学给出的空间分辨率实验结果为0.7mm,但是由于没有合适的测量基准,该结果并不是直接的测量结果,而是根据共振线宽测量值的计算结果。实验中分别采用均匀光和非均匀光进行自旋极化率空间操控,其测量结果如图 1(b)所示。
德国Stuttgart大学从低场磁共振成像的角度出发,开展了原子气室内自旋极化率分布的研究[4-5],所采用的自旋极化率操控方法为光学掩模方法。据报道,实验中可分辨0.5mm小孔产生的极化率分布[4]。 测试方案的时序图如图2(a)所示, 首先施加Bx方向的磁场和脉冲抽运光,抽运结束后利用检测光测量系统的T1,然后关闭Bx并施加Bz和梯度场Gx(z)(y方向测量采用同样的方法), 测试梯度场下的自由振荡衰减信号。基于对该信号的频谱分析,获得对应不同位置自旋极化率的大小。该方案与美国Princeton大学的方案相比,没有进行射频场(或者B)的扫描。极化过程不施加梯度场,因此可以消除梯度场造成的弛豫和低极化问题。

图2 德国Stuttgart大学的光操控/磁测量方法Fig.2 Optical manipulation/magnetic measurement method developed by Stuttgart University
德国Stuttgart大学也对测量空间分辨率进行了理论分析,给出了空间分辨率的计算公式
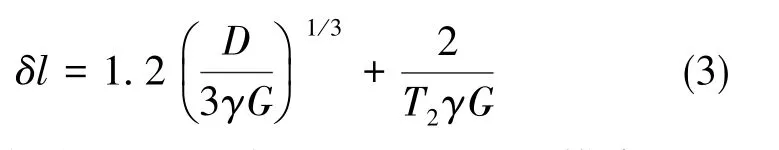
当梯度较大且T2足够长时,空间分辨率主要由T2*决定。将美国Princeton大学的临界梯度公式代入,可得空间分辨率的极限为δl=0.83
瑞士Fribourg大学从测量自旋扩散特性的角度出发,开展了 MRI自旋极化率分布测量的研究[6-7]。 采用如图 3(b)所示小孔直径为 1mm 的掩模板,对原子气室内的自旋极化率分布进行了操控,操控时序图如图3(a)所示。之后采用MRI方法进行了极化率分布的检测,测试结果如图3(c)所示[6]。在MRI测试中,与德国Stuttgart大学的研究方案相比,瑞士Fribourg大学的研究方案中没有进行磁场方向的转换,而是通过π/2脉冲,将极化后的自旋旋转90°,其效果与切换磁场方向基本相同。瑞士Fribourg大学采用对应小孔测量所得的线宽,推断该测量实验系统的空间分辨率约为360μm。


图3 瑞士Fribourg大学的光操控/磁测量方法Fig.3 Optical manipulation/magnetic measurement method developed by Fribourg University
日本Kyoto大学采用光纤输出的环状条纹光进行自旋极化率的空间操控,在测量中加入了自旋回波技术,其测试光路和磁场方案如图4(a)所示,操控时序图如图4(b)所示,最终的测量结果如图 4(c)所示[8]。 另外, 日本 Kyoto 大学也尝试了掩模板操控方法,最终的实验空间分辨率为2mm[8-9]。


图4 日本Kyoto大学的光操控/磁测量方法Fig.4 Optical manipulation/magnetic measurement method developed by Kyoto University
另外,美国Los Alamos国家实验室也开展了自旋极化率的空间光操控/磁测量研究,并将梯度回波技术应用其中,获得了原子气室内自旋极化率的三维分布,其空间分辨率达到0.8mm×1.2mm×1.4mm[10]。
2 磁操控/光测量方法
磁操控/光测量方法利用环境磁场的不均匀性、主动磁场线圈或磁纳米颗粒操控自旋极化率在空间的分布,然后通过光电探测阵列或CCD对不同区域的光场进行测量,从而获得自旋极化率空间分布信息。
2003年,美国Princeton大学首次采用光电探测阵列对磁屏蔽环境下原子气室中由于梯度导致的极化率空间分布进行了测量[11]。测试光路如图5(a)所示,光电探测阵列为1×7阵列,相邻探测单元的距离为3mm。图5(b)中的内嵌图给出了自旋极化率空间操控方法的示意图,在气室顶部5.3cm的位置放置电流环以产生磁场梯度,从而使自旋极化率出现不均匀的空间分布。图5(b)为根据光电探测阵列测量到的极化率计算得出的对应位置磁场大小。2006年,美国Princeton大学采用16×16的探测阵列进行了原子气室内自旋极化率空间分布的测量。并以此为基础,反推出控制极化率分布的脑磁信号[12]。2014年,美国Princeton大学采用256×256的探测阵列,再次完成了脑磁控制的自旋极化率空间分布测量[13],并且对原子气室内自旋极化率的空间分辨率进行了讨论,定义了无扩散干扰距离并为后续的研究提供了重要设计原则,即探测阵列的间距要大于无扩散干扰距离。

图5 美国Princeton大学的磁操控/光测量方法Fig.5 Magnetic manipulation/optical measurement method developed by Princeton University
美国Sandia国家实验室针对脑磁探测需求,采用2×2的差分探测阵列进行自旋极化率的空间分布探测,其基本测试方案如图6所示,探测点之间的间隔为 18mm[14-16]。

图6 美国Sandia国家实验室的自旋极化率空间分布光测量方案Fig.6 Spin polarization spatial measurement scheme using optical method at Sandia National Laboratory
以色列Ben-Gurion大学采用5×5光电探测阵列和抽运光切片技术,获得了原子气室内自旋极化率的三维分布,测试方案如图7所示,三维像素分辨率为 2mm×2mm×2mm[17]。

图7 以色列Ben-Gurion大学采用的测试方案Fig.7 Measurement scheme used by Ben-Gurion University
日本Kyoto大学采用光电探测阵列和CCD对K-Rb混合气室内的自旋极化率分布进行了测量[18-19],其自旋极化率分布的操控仍然通过气室顶部放置的电流环线圈,如图8所示[18]。在使用CCD的过程中,发现由于背景光强造成的Bloom和Smear现象比较明显,因此不得不降低抽运光光强,这就会导致信号的下降。最终,每个通过的信号为 64×32(像素),基于单像素尺寸 26μm×26μm,可知每个探测单元的尺寸为1.66mm×0.83mm。日本Kyoto大学在2014年之后的设计中,均以美国Princeton大学2014年提出的无扩散干扰距离[13]作为空间分辨率极限,并以此进行相邻测试单元间隔距离的设计,即间隔距离大于无扩散干扰距离。
瑞士Fribourg大学利用磁纳米颗粒操控原子气室内自旋极化率的空间分布,通过CCD测量不同位置的自旋极化率导致的荧光强度变化,由此获得自旋极化率的空间分布信息[20-21]。再借助该信息反推纳米颗粒的位置,其基本方案如图9所示[21]。
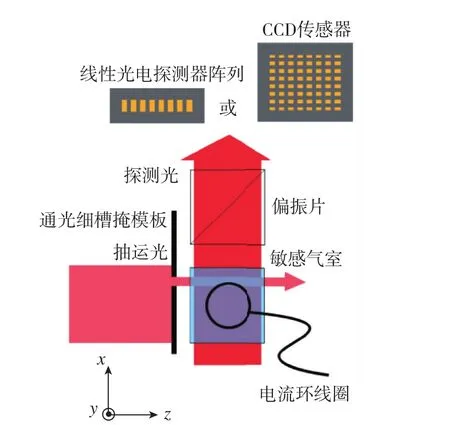
图8 日本Kyoto大学采用的磁操控/光测量方案Fig.8 Scheme of magnetic manipulation/optical measurement used by Kyoto University
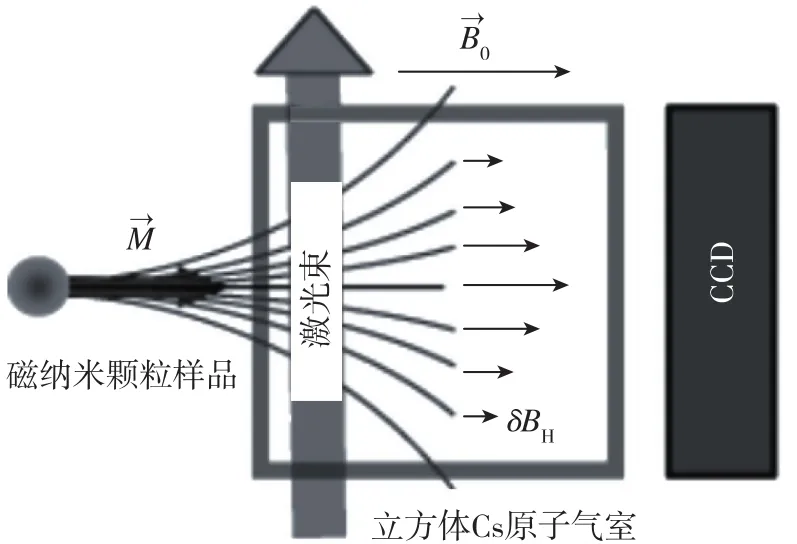
图9 瑞士Fribourg大学采用的磁操控/光测量方案Fig.9 Scheme of magnetic manipulation/optical measurement used by Fribourg University
浙江大学和浙江工业大学面向脑磁形成的原子气室内自旋极化率空间分布,采用四像素的光电探测阵列进行测试[22-23],并结合参数调制方法[24],实现了2个正交方向磁场的同步探测。在探测阵列的间距设计中,与日本Kyoto大学类似,根据美国Princeton大学的研究[13],以计算结果作为空间分辨率极限进行了设计。
3 光操控/光测量方法
利用抽运光的不均匀性或光学掩模板虽然可以实现原子自旋极化空间分布的操控,但是对于操控的结果却很难再利用光探测的方法进行检测,原因是通过掩模板形成的结构光分布一般要远大于极化率分布对光产生的影响。也就是说,即便能够对光进行测量,其结果也主要决定于光强自身的分布,而不是自旋极化率的分布。针对这种情况,笔者所在的研究小组提出了基于DMD的时空双重调制操控方法和正交隔离测试方法[25-26],其基本实验方案如图10所示,主要的实验组件有激光器及其光学调整组件(包含空间光滤波器、准直透镜、偏振片和1/4波片等)、DMD数字微镜系统、原子气室及其加热温控模块、磁屏蔽及磁场控制模块、CCD探测器等五部分。其中,激光器是美国Photodigm公司的DBR激光器,DMD系统采用德国Vialux公司的V-6501型DMD及其控制模块,加热和温控模块采用氮化硼材料和无磁合金加热丝,通过双绞结构和高频驱动消除加热电流产生的静磁场。

图10 光操控/光测量方法实验方案图Fig.10 Experimental setup of optical manipulation/optical measurement method
3.1 时空双重调制操控方法
采用DMD可以实现与掩模板相同的空间操控效果,但是如前所述,这种操控方法的结果是光探测的结果为抽运光自身的分布。时空双重调制操控方法完全解决了这一问题,不仅能实现微米尺度的自旋极化率操控,而且输出光强的分布完全由自旋极化率决定。具体实现方法如图11所示,激光在横截面上任意区域均为脉冲光,即时间上做了调制;在空间上,不同区域的时间调制频率不同,相当于做了空间调制。如果此时外磁场B远离调制频率w1和w2, 则空间上任一点处的自旋极化率接近为零,此时输出光强在空间各点处相等(实验中采样频率远小于激光自身调制频率)。也就是说,不存在抽运光自身的光强分布。改变磁场B使得其与w2共振,此时对应区域的自旋被极化,形成自旋极化率的空间分布,自旋极化率的空间分布造成输出光强的重新分布。此时,探测光强的分布即可得到自旋极化率的分布。
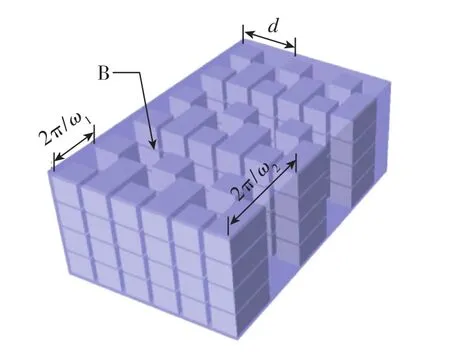
图11 时空双重调制光操控原理示意图Fig.11 Scheme diagram of temporal-spatial double modulation optical manipulation
3.2 正交隔离测量方法
前述方法虽然消除了光强自身分布对极化率测量的影响,但是由于仍然存在较大的背景光强,如果采用CCD进行探测,就会出现Bloom和Smear效应。针对这一问题,在文献[27]的启发下,提出了正交隔离测量方法。
该方法采用1个偏振片和1个1/4波片生成椭圆偏振光,以椭圆偏振光进行抽运,在激光从原子气室出射后通过1个1/4波片,将椭圆偏振光转换为线偏振光,之后再通过1片正交的线偏振片将输出光彻底隔离。当外磁场远离所有光调制频率时,气室内任意点处的自旋极化率均为零,CCD将不会探测到任何信号。也就是说,背景图案为全黑图案。当外磁场与w2共振时,对应区域的自旋极化率不为零,椭圆偏振光发生旋光效应,导致无法实现完全隔离,对应区域的CCD就会探测到相应的信号。
在该方法中,第1个偏振片与1/4波片的角度是关键参数。为了对该参数进行优化,采用Jones矩阵对整个测量过程进行了建模,具体如下:
1)在第1个偏振片和1/4波片之后,光变成椭圆偏振光,包括2个具有相反螺旋度的圆偏振分量,其Jones矩阵可以表示为
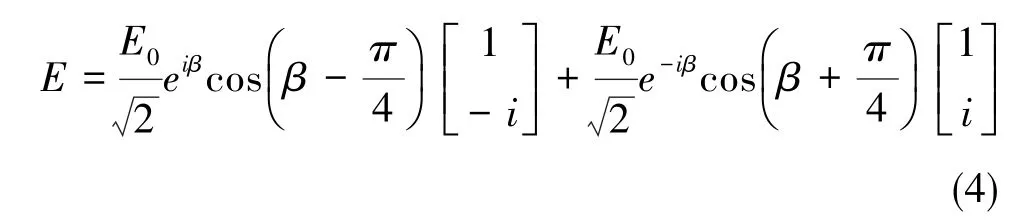
2)在气室中的原子同时受到左旋圆偏振光和右旋圆偏振光的作用,最终的极化率为

3)光经过极化的原子气室后,由于Faraday旋光效应,光的偏振面会发生偏转,旋光角φ正比于自旋极化率Pz
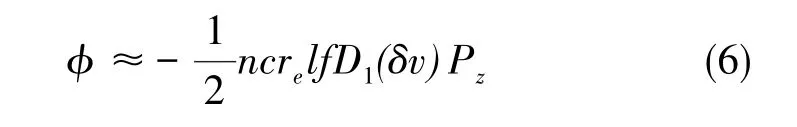
式(6)中,n为原子密度,c为光速,re为电子半径,l为气室长度,f为振荡强度,D1(δv)为D1线附近的归一化吸收系数。
气室的Jones矩阵可以表示为

4)为了实现正交隔离,设置第2个偏振片相对于第1个偏振片之间的相对角度为2β+π/2。经过第2个线偏振片的输出激光的振幅Eout如下

式(8)中,GP2和GQW2分别为第2个线偏振片和第2个1/4波片的Jones矩阵,其表达式分别如下

根据式(8)计算输出激光强度和相对角度β之间的关系,如图12所示。在同样的自旋极化率情况下,时的输出光强信号达到最大值。

图12 经过第2个线偏振片后的输出光强与β的函数关系Fig.12 Function relationship between the output light intensity and β after passing through the second linear polarizer
3.3 实验结果及讨论
实验采用3.1节中所述的时空双重调制操控方法和3.2节中所述的正交隔离测量方法,并设置参数完成了原子气室内自旋极化率空间分布的操控和测量,结果如图13所示。其中,图13(a)为正交隔离后的背景图像;图13(b)为加磁场后由于时空双重调制产生的自旋极化率分布图像;图13(c)为通过前两幅图相减去除背景后的结果,中心部分的条纹宽度为54.8μm;图13(d)为更细微的成像,绿色矩形区域内的条纹宽度为13.7μm。

图13 原子气室内自旋极化率的操控与测量结果Fig.13 Results of spin polarization manipulation and measurement in atomic cell
图13的测试结果表明, 文献[13]、 文献[19]、文献[23]和文献[28]所提出和使用的无扩散干扰距离很可能并非原子气室内自旋极化率空间分辨率的理论极限。因此,以下从自旋扩散和量子测不准原理出发,对空间分辨率的理论极限进行分析讨论。
考虑空间周期为d(即相邻单元的空间距离)且频率大小相间变化的抽运光场分布,由于共振和非共振的原因,必然会使得自旋极化率大小也相间变化,其调制幅值为ΔP。 计算方法如下:
1)首先,根据自旋Fick扩散定律和Bloch方程,得到共振和非共振区域中的横向自旋极化率稳态方程

2)再以自旋极化率连续可导作为约束条件求解式(11),得到共振和非共振处的平均自旋极化率
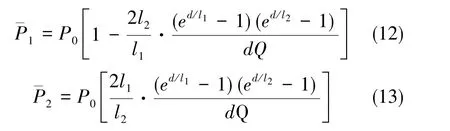
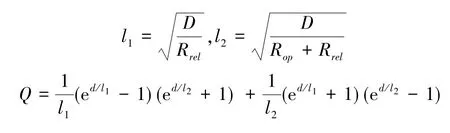
由式(12)和式(13), 可得到相邻通道之间的极化差异为

由式(14)可知,由于扩散的影响,能够操控实现的自旋极化率空间差异与空间距离有关。在其他参数不变的情况下,相邻操控和测量单元的最小距离d越大,可实现的极化率差异ΔP也越大。
另外,根据不确定性原理可知,自旋投影噪声与原子数相关。随着空间距离的缩小,用于测量的原子数减少。自旋投影噪声可用下式表示
式(15)中,q为衰减因子,n为原子密度,A为原子气室的横截面积,t为测量时间。
根据式(14)和式(15)绘制的典型曲线如图 14所示。可以看出,随着测量间距的缩小,由于测量原子数减少,自旋投影噪声δP变大,而扩散则导致相邻区域的自旋极化率差值ΔP减小。
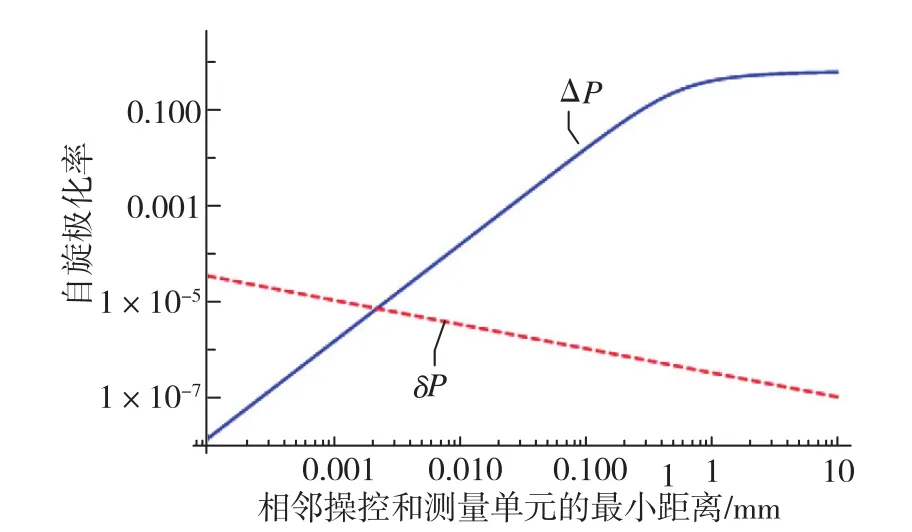
图14 自旋极化率在相邻单元的差值/自旋极化率量子噪声与相邻操控和测量单元的最小距离之间的关系Fig.14 Relationship between adjacent pixels spin polarization difference/spin polarization quantum noise and the minimum adjacent pixels distance
由图14可知,两条曲线在某一位置相交,在交点右边,可操控的自旋极化率空间差异ΔP大于测量量子噪声δP,该尺度的自旋极化率空间分布线条可分辨;在交点左边,ΔP小于δP,该尺度的线条不可分辨。因此,定义交点处对应的距离为原子气室内自旋极化率空间操控和测量的分辨率。对于不同的原子气室参数,会有不同的空间分辨率,图14中对应的空间分辨率为2μm。
4 其他相关研究
除了上述三类主要的研究之外,在原子气室内自旋极化率空间操控与测量方面,还有一些值得关注的研究。日本Kyoto大学曾尝试过采用远离共振频率的不同频率斩波器进行空间信号定位的方法[28],这种方法与磁共振成像方法的类似之处在于最终都要通过频率分析来确定不同空间位置自旋极化率的大小。但是由于斩波器的体积较大,难以实现高的空间分辨率。美国Los Alamos国家实验室采用磁通阵列的方法,将外部磁场分布通过磁通结构导入到原子气室内,从而实现气室内自旋极化率空间分布的操控[29]。通过该方法可改变自旋极化率分布和操控磁场分布的空间比例,从而提高操控或测量的空间分辨率。瑞士Basel大学通过微波场幅值的空间分布来控制原子气室内自旋Rabi振荡频率的空间分布,这导致随着时间的推移,原子气室内自旋极化率的空间分布在不断变化。测量过程中,首先对自旋进行极化,之后采用10μs的快速脉冲光测量不同时刻气室内光深度(Opticaldepth)的分布,从而得到自旋极化率的实时分布,也可利用测量结果反推微波场的分布[30]。日本国立Okayama大学单纯采用微波场的空间分布来操控自旋极化率的空间分布,采用Mx磁测量原理进行自旋极化率测量。由于该测量方法需要进行信号的解调,所以必须采用高速分布式光电信号探测器件,常规的CCD不能满足要求。日本国立Okayama大学采用DMD和光电探测器相结合的方案,对50×50个单元进行了逐一测量[31]。
5 结论
本文对三类典型的原子气室内自旋极化率操控和测量方法进行了综述和介绍。其中,光操控/磁测量方法主要采用光学掩模板的方式操控原子气室内自旋极化率的空间分布,采用磁共振成像的方式对自旋极化率空间分布进行测量;磁操控/光测量方法主要采用由线圈或生物体产生的磁场梯度控制自旋极化率的空间分布,通过光电探测阵列探测不同位置光信号的方式测量自旋极化率的空间分布;光操控/光测量方法采用光场的时间和空间双重调制进行自旋极化率空间分布的操控。由于该操控方法能实现等光强操控掩模,因此可以同时采用光探测的方法进行自旋极化率的测量。采用正交隔离测量方法,进一步降低了背景信号,提高了信噪比。光操控/光测量方法实现了13.7μm宽度线条的自旋极化率空间操控与测量。最后,基于自旋扩散和量子测不准原理,分析讨论了自旋极化率的理论极限,给出了计算理论极限的基本模型和判定准则。
