基于数学建模素养的立体几何教学设计实践探究

赵玉香

【摘 要】 教学设计是课堂教学的“罗盘”，立体几何教学是提升学生数学建模素养的重要载体。本文从三个方面介绍了实践探究中形成的基于数学建模素养下的形形相联六环节立体几何教学设计模式。

【关键词】 形形相联;六环节立体几何教学设计;数学建模核心素养

一、问题的提出

2017年开始，数学新课标、新高考评价体系越来越重视学生的核心素养，特别是数学建模素养。当下高中学生的数学建模核心素养较弱，从而导致其应用数学知识解决问题的能力较弱。怎样的教学设计能更好地服务课堂、有效提升学生的数学建模素养呢？教无定法，贵在得法，笔者决定从多面体的外接球问题着手，对立体几何教学设计开展具体的实践研究，以期得到有实效的教法。

二、问题的分析、探究及解决

（一）指导理论与概念

学科素养是高考评价体系“一体四层四翼”中的四层考查目标之一，数学素养包含具有数学基本特征的必备思维品格和关键能力，是数学知识、技能、能力及情感、态度、价值观的综合体现。《高中数学新课程标准》明确提出数学建模是高中数学六大核心素养之一。 数学建模的实质是将实际问题的内在规律用数字、图表或公式、符号等表示出来，根据数学基础知识和基本原理建立数学模型的若干原型，在解决实际问题时识模、用模、解模的过程。

（二）问题探究

1.高中学生数学建模素养弱的主要成因

（1）快餐式的课堂教学忽略知识的来龙去脉，学生对数学知识“只窥一斑”、不探全貌，思维深度与习惯不佳，数形结合意识不强。

（2）学生的课堂反思与归纳不足，不能精准掌握数学知识与方法。

2.提升数学建模素养的立体几何教学设计实践探究

（1）流程设计探究：教学过程设计分为几个环节更合适？每个环节的具体任务是什么？该怎么落实？

（2）关键环节设计探究：如何引导学生形形相联，联想并构建相应的数学模型来解决问题，从而有效提升学生的数学建模素养？

（三）问题解决及模式形成

笔者认为，形形相联，以图形为主线的六环节立体几何教学设计模式能有效提升学生的数学建模核心素养：（1）目标引领中展示问题;（2）回顾旧知中挖掘内涵;（3）问题引导中建模研模;（4）问题实践中用模解模;（5）反思归纳中完善模型;（6）实践巩固中熟知模型。

三、模式实施

多面体外接球问题是高中立体几何教学中的一个重点和难点，本文以此为例可以更好地阐述形形相联六环节立体几何教学设计模式。

（一）目标引领中展示问题

图形展示三棱锥、四棱锥与棱柱等多面体及其外接球，明确学习目标：“能根据几何体的性质特征，解决一些简单的多面体的外接球问题”。

（二）回顾旧知中挖掘内涵

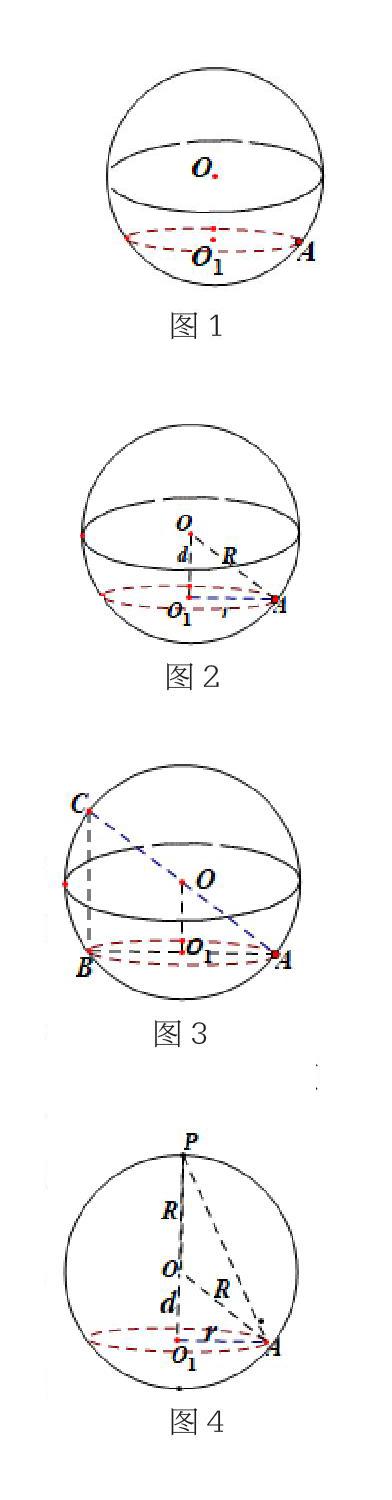
引导学生观察图1，设置问题，回顾多面体和球的几何性质，为新课奠定基础。

1.概念与性质回顾

（1）球的定义是什么？有哪些性质？

（2）平面上，三角形的外接圆圆心如何确定？

（3）空间中，多面体的外接球球心如何确定？

2.內涵领悟（展示几何体实物）

（1）长方体的外接球球心在哪儿？它的半径怎么计算？

（2）正四面体的外接球球心在哪儿？它的半径怎么计算？

【设计意图】以学生熟悉的长方体和正四面体的外接球问题为切入点，引导学生明确外接球问题的内涵是确定球心和半径——球心到各顶点距离相等，半径等于球心到任一个顶点的距离。

（三）问题引导中建模研模

1.建模：通过上面的问题可得外接球问题的原型（图2）。

2.研模：所有多面体的外接球问题都可构建为图2原型，经常会出现下面两种实际问题解决方法：

（1）构造三边长含有R、r和d的直角三角形。

代表模型：图3。

【设计意图】将外接球原型扩展可得一个新的直角三角形（图3），其中，BC垂直小圆所在平面，引导学生由图形联想到其特征“线面垂直”，侧棱垂直底面。可联想到长方体具备此特征，“长方体的8个顶点中，任取若干个顶点组成的多面体，其外接球也是原长方体的外接球”，一些多面体的外接球问题可通过补形法转化为长方体的外接球，运用图3模型来解决。

（2）定义法：确定球心的位置，球心到各顶点距离相等。

球心与多面体任意一面的外心连线与此平面垂直。代表模型如图4。

【设计意图】外接球原型也可扩展为图4的模型，引导学生由图形联想到可确定球心位置的一些多面体，特别是椎体的外接球问题可构建此模型来解决。

正四面体的外接球既可转化为长方体的外接球，也可用图4模型来解决。

（四）问题实践中用模解模

1.线面垂直模型的应用

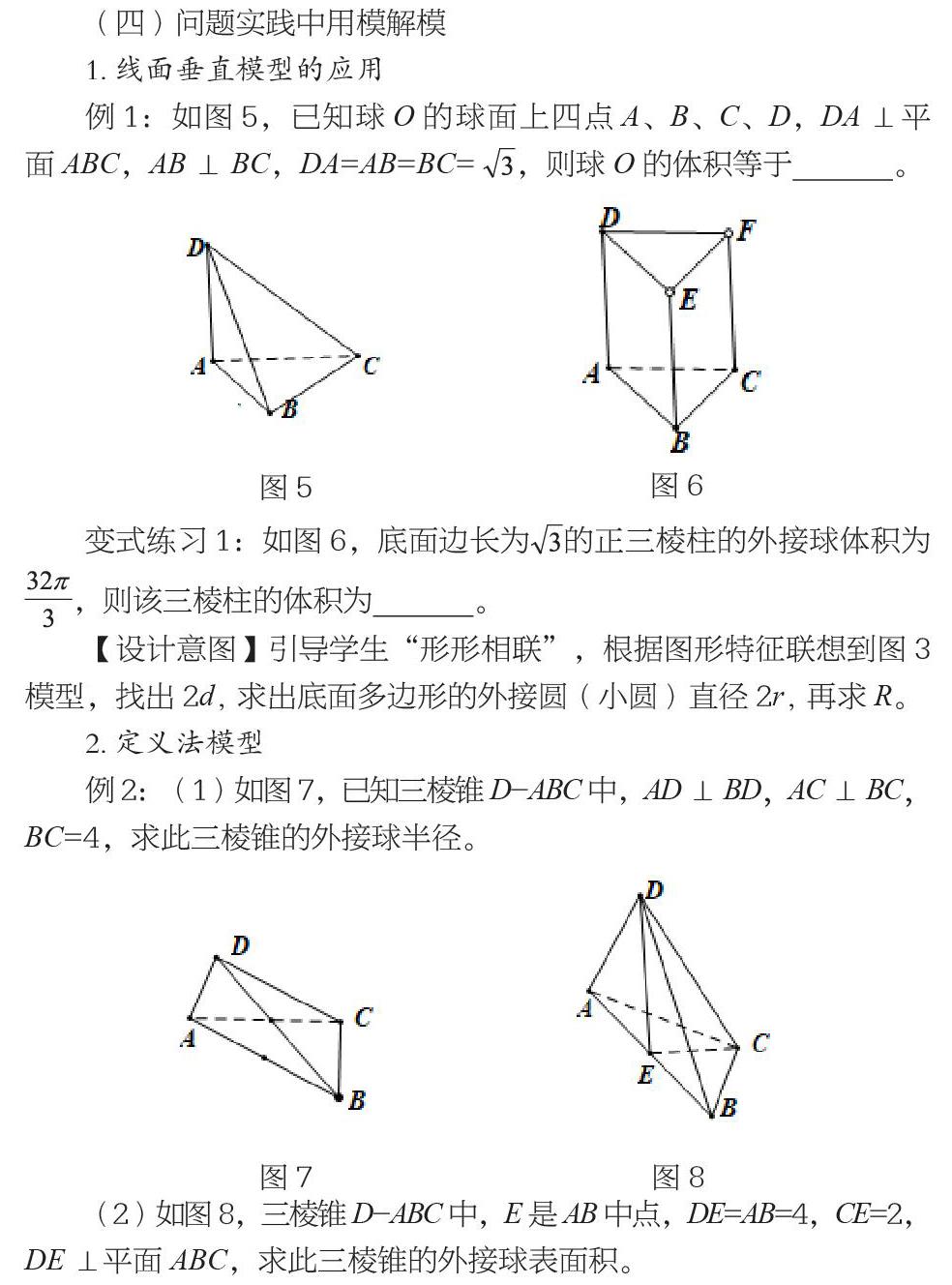
例1：如图5，已知球O的球面上四点A、B、C、D，DA⊥平面ABC，AB⊥BC，DA=AB=BC=，则球O的体积等于            。

变式练习1：如图6，底面边长为的正三棱柱的外接球体积为，则该三棱柱的体积为            。

【设计意图】引导学生“形形相联”，根据图形特征联想到图3模型，找出2d，求出底面多边形的外接圆（小圆）直径2r，再求R。

2.定义法模型

例2：（1）如图7，已知三棱锥D-ABC中，AD⊥BD，AC⊥BC，BC=4，求此三棱锥的外接球半径。

（2）如图8，三棱锥D-ABC中，E是AB中点，DE=AB=4，CE=2，DE⊥平面ABC，求此三棱锥的外接球表面积。

变式练习2：正四棱锥的五个顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为            。

【设计意图】引导学生根据球的定义和性质明确“球心在过多面体任意面的外心且与此平面垂直的直线上”，将此类问题分解为找多边形的外心、确定球心位置、构建并求解图4模型几个步骤。

（五）反思归纳中完善模型

引导学生归纳反思：例题及变式练习是否还有其他的解法？具有什么明显特征的外接球问题可以选用图3和图4模型来解决？

（六）实践巩固中熟知模型

巩固练习1：底面边长为1，侧棱长为的正四棱柱的外接球的体积为            。

巩固练习2：直三棱柱的各顶点都在同一球面，AB=3，AC=5，BC=7，，则此球的表面积等于              。

巩固练习3：三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形，AB=2，SA=SB=SC=2，则此三棱锥的外接球球心到平面ABC的距离是             。

實践发现，用这种教学设计为立体几何教学做准备，可更好地引导学生构建数学模型，形形相联，以不变的基本模型解决万变的实际问题，有效提升学生的数学建模素养。这种教学设计模式需要教师认真研读课程标准与大纲要求，预测学生可能出现的问题，认真整合与重组教材内容，有序细化相关问题与对应数学模型所需的必备知识，如此才能引导学生建模、用模和解模，不断渗透并提升学生的数学核心素养。

【参考文献】

[1]林军，陈翰林，刘启宽.数学建模教程（31版）[M].北京：科学出版社，2018.2.

[2]史宁中.数形结合与数学模型——高中数学教学中的核心问题[M].北京：高等教育出版社，2018.

[3]林日福.基于数学核心素养的教学研究[M].重庆：西南师范大学出版社，2018.

[4]王国江，张倬霖.基于核心素养的数学创新教学设计[M].上海：社会科学出版社，2018.

【备注：本文系广州市教育科学规划2018年度课题《基于核心素养的高中数学教学设计实践研究》（课题批准号：20190000095）的研究成果】