基于小生境鱼群算法的有限元模型修正多解问题研究*

康俊涛，张学强，张亚州，秦世强，曹鸿猷，连岳泉

(武汉理工大学土木工程与建筑学院，湖北 武汉 430070)

桥梁结构中的有限元模型通常依据设计图纸建立，隐含了多种理想化假定，从而使得理论分析结果与结构实际响应存在一定误差，而精确的桥梁有限元模型对评估在役桥梁的抗震抗风性能、结构损伤识别及桥梁健康状况监测是至关重要的[1]。模型修正技术通过修改初始有限元几何参数、物理参数、边界条件等信息从而使有限元模型计算值与实测值更接近[2]。目前，国内外很多学者做了有关桥梁模型修正的研究。韩建平等[3]分别采用含有交叉项与不含交叉项的响应面作为代理模型，根据现场实测动力特性对刚构-连续组合桥梁进行修正，修正后的模型更能精确反应桥梁实际动力响应；彭涛等[4]联合动、静力学特性对一座混凝土斜拉桥进行模型修正，不仅参与修正的动、静力响应与实测值接近，且未参与修正的动、静力响应也与实测值更加接近。这些模型修正技术存在一个共同特点：通过采用高效的智能算法优化模型结构参数，得到一组使得有限元模型计算值与实测值误差最小的全局最优解。然而，由于荷载试验过程中传感器个数有限、测量数据不充分及测量误差的存在，或者在模型优化中未充分考虑影响结构响应的因素，使得优化得到的某组全局最优解并不能代表实际结构的真实参数，目标函数存在的其他全局最优解或局部最优解可能比该组全局最优解更能代表实际结构的参数[5-6]。在国内，陈学前等[7]指出：只采用一组修正结果的模型修正方案，修正后的模型与结构的实际响应仍可能存在误差。因此，能够产生多解的模型修正技术(modeling to generate alternatives，MGA)应用而生。MGA为决策者提供的其他全局最优解或局部最优解所产生的目标值与已产生的全局最优解相同或接近，但它们的解空间却处于不同的位置。决策者可根据实际工程经验，权衡各方面利弊，在所有的最优解或局部最优解中选出一组或者多组，减少对结构实际参数误判的可能[8]。

MGA修正技术与多目标寻优有着本质区别，MGA适用的目标函数只有一个，需找到使得一个目标函数值最优或较优的多个全局最优解或多个局部最优解。而多目标寻优产生的多个解集适用的目标函数为多个，如优化参数值使得模态误差与挠度误差两个目标函数值最小。MGA技术已经成功应用在多个领域，包括数学领域中的多峰值函数寻优、工程领域中的抗震设计及结构优化设计、航空路线规划设计等。国外，已有学者将MGA运用在模型修正上，如：Boris A. Zárate等[8]通过数值仿真分析验证了MGA的可行性后，将该技术应用在一座斜拉桥的模型修正上，修正结果产生了4组解，它们的目标函数值接近但解空间却截然不同。

在国内，鲜有学者将MGA应用在有限元模型修正上。本文提出了一种改进的小生境鱼群算法，将传统的人工鱼群算法(artificial fish swarm algorithm，AFSA)融合小生境技术[9]与反向学习策略[10]，并在算法运行后期采用模拟退火算法进行局部细化寻优，克服了传统AFSA算法在寻找函数峰值时难以同时找到多个峰值、对初值敏感、寻优结果精度不高的弊端[11]。通过数值仿真分析，验证了小生境鱼群算法的可行性；接着将该算法应用在一座缩尺斜拉桥模型的修正上。

1 有限元模型修正的多解问题

传统的有限元模型修正技术是通过智能算法找到一组参数值使得模型误差达到最小，忽略了可能存在的多组全局最优解；且，由于传感器数量有限，测量数据不充分以及仪器识别存在误差，局部最优解可能比全局最优解更能代表结构实际参数。模型修正的多解理论为决策者提供了多组解，这些解都具有减少模型理论误差的功能，区别在于它们的解空间处于不同的位置。图1很好地诠释了有限元模型修正多解的原理。函数g(x,y)为二元函数，以最小值作为最优解对应的解集有2个，这两个解集能同时满足g(x1,y1)=g(x2,y2)=min(g(x,y))；次优解有1个，满足|g(x3,y3)-min(g(x,y))|=ε，ε为常数，起到控制是否接受次优解的功能。

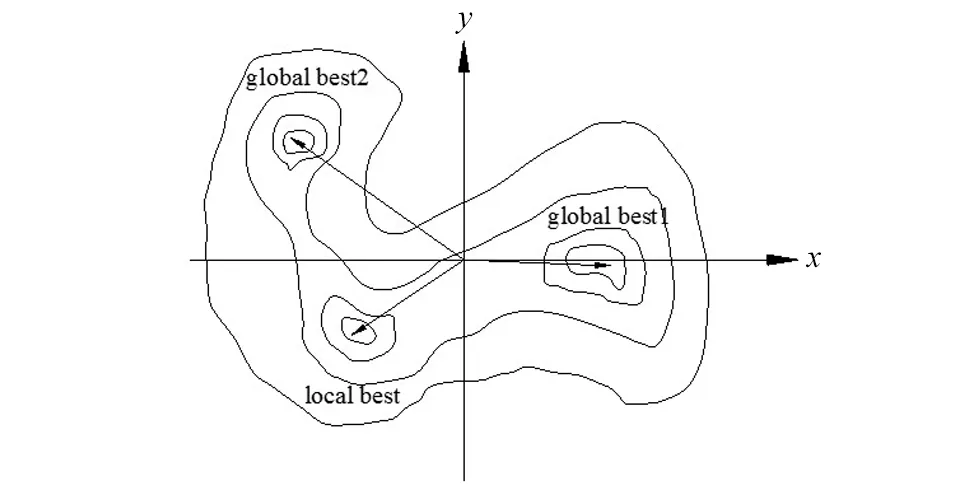
图1 双变量模型修正多解问题的可行区域

为找到有限元模型修正的多组解，本文提出了一种改进的小生境鱼群算法，使用该算法找到目标函数的最优解或次优解，目标函数表达式如式(1)所示：

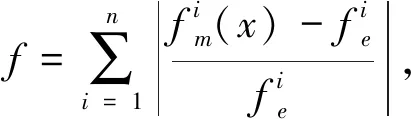
x∈[VLB ,VUB ]

(1)

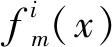
2 改进的小生境鱼群算法及数值仿真

分析

2.1 改进人工鱼群算法策略

传统的人工鱼群算法[12]存在以下三个问题： ① 对于存在多个全局最优解或多个局部最优解的函数，该算法运行一次只能找到其中一个最优解，多次执行优化并不能保证收敛到所有解； ② 人工鱼群移动步距设定为固定值，当算法执行到后期，人工鱼在全局最优值附近震荡，收敛速度减慢，优化精度低； ③ AFSA算法采用随机生成的方式确定鱼群初始坐标点，对初值敏感。基于此，本文提出一种改进的小生境鱼群算法，从以下三方面改进：

1)将小生境技术与AFSA算法结合，引入小生境半径来控制鱼群之间的距离。每次执行AFSA算法后，对最优解进行判断，满足要求后放入小生境核内，在下次执行AFSA算法的每代中，通过初始化方式控制人工鱼与小生境核内已有的最优解的距离，使得当前鱼群往新的领域搜索，从而获得函数的多个全局最优解及局部最优解。具体操作如下：

①初始化小生境核内人工鱼群坐标点，根据鱼群各维度参数定义域长度设置小生境半径R，取值建议如式(2)所示：

(2)

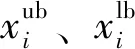
②在执行鱼群算法迭代的每代中，计算当代鱼群与小生境核内已存最优解的人工鱼的距离，并将距离与小生境半径进行比较，若在半径范围内，则初始化该人工鱼位置；

③将每次执行AFSA算法所得到的最优解与小生境核内已存的最优解比较，若优于任意一个，则将该最优解放入小生境核内；否则放弃，继续下一轮循环，直到找到所有局部最优解及全局最优解或满足算法终止条件。

2)将每一次执行AFSA算法所得到的最优解采用模拟退火算法进行局部细化寻优，提高算法的优化精度。具体操作如下：

①执行AFSA算法各步骤，找到最优解bestx；

②设置模拟退火算法初始温度T0，终止温度Tend，确定每个温度下的迭代次数L；

③让最优解bestx产生一个随机扰动，得到一个新解bestx’；

④判断bestx’的适应度值是否优于bestx的适应度值，若是则接受；否则，判断exp(-df/T)>rand，若是，仍然接受bestx’，否则放弃。重复步骤③与④，直到满足终止温度条件。其中，df=f(bestx’)-f(bestx)，rand为0～1之间的随机数。

3)引入反向学习的种群策略，鱼群在初始化种群产生n条人工鱼后，利用反向学习策略生成当前人工鱼位置的对立点，从而增加种群的多样性，加快AFSA算法的收敛速度，有效解决AFSA对初值敏感、迭代过程中由于超级个体存在陷入局部最优的问题。具体操作如下：

①初始化种群后第i条人工鱼位置为xi(xi1,xi2,xi3,…,xim)，根据反向学习策略，第i条人工鱼第m维的对立参数取值如式(3)：

(3)

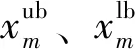
②每次迭代分别计算当前人工鱼及利用反向学习策略得到的人工鱼适应度值，将2n组适应度值按照递增或递减的顺序排序，筛选出较优的前n组作为当前代数人工鱼群。

2.2 数值实验及分析

为测试本文所提小生境鱼群算法的性能，选取三个典型的多峰函数进行了仿真测试，并将优化结果与AFSA算法优化结果进行比较。测试函数如式(4) - (5)所示，小生境鱼群算法的参数设置如表1所示。

f1(x,y)=cos(2πx)×cos(2πy)

×e-(x2+y2)/10

-1≤x,y≤1

(4)

f2(x,y)=200-(x2+y-11)2

-(y2+x-7)2

-6≤x,y≤6

(5)

将小生境鱼群算法运行5次；AFSA算法运行5组，每组运行13次，测试函数1的运行结果如表2所示。

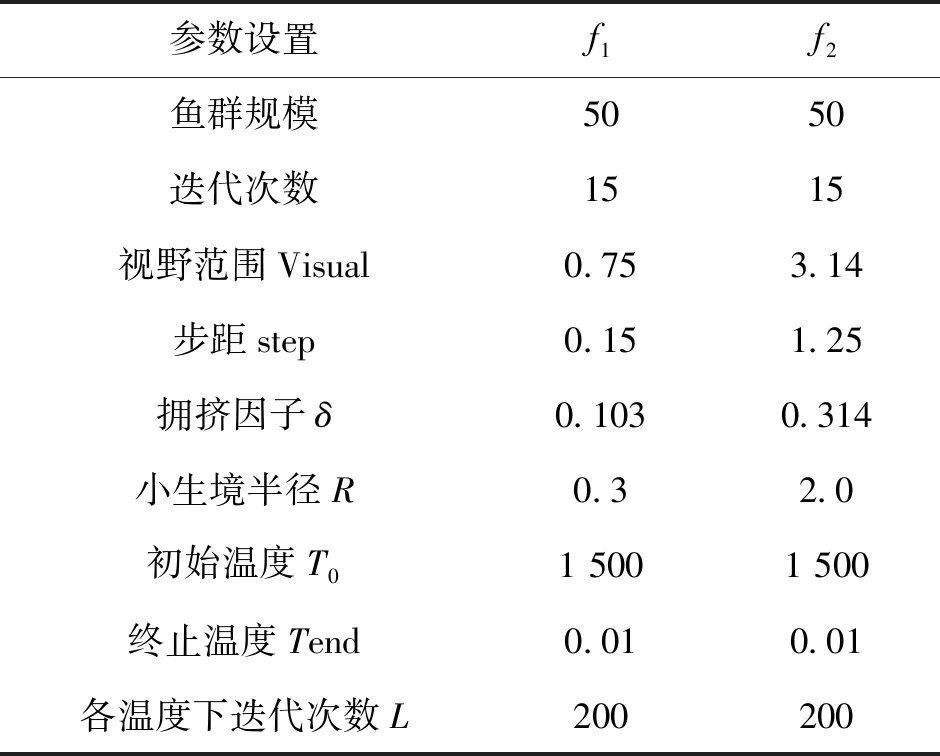
表1 测试函数对应的小生境鱼群算法的参数设置值

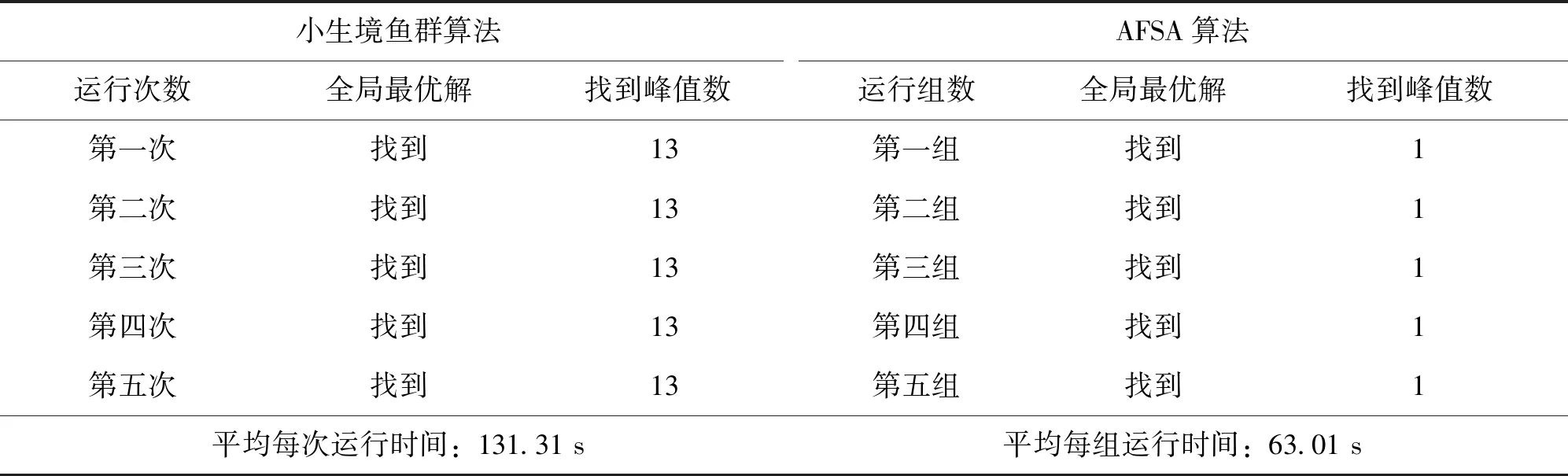
表2 小生境鱼群算法及AFSA算法优化函数f1的统计结果

由表2、图2可知，小生境鱼群算法运行5次，每次均能找到f1的13个峰值点。而，AFSA算法运行5组，每组只能找到f1的一个全局最优解，忽略了所有的局部最优解及4个角点峰值点。

将小生境鱼群算法运行5次；AFSA算法运行5组，每组运行4次，测试函数2的运行结果如表3。由表3、图3可知，小生境鱼群算法运行5次，每次均能找到f2的全部全局最优解。AFSA算法其中一组运行结果分别如下：

f2(-3.768 343，-3.277 694)= 199.993 398

f2(3.596 599，-1.870 760)= 199.986 524

f2(-2.799 671，3.138 028)= 199.997 172

f2(-3.778 259，-3.288 557)= 199.998 502

f2(-2.808 160，3.131 370)= 199.999 699

对比结果表明，AFSA算法通过多次运行并不能保证收敛到函数所有全局最优解，且全局最优解存在精度不高问题，而小生境鱼群算法能够更精确地找到f2的所有全局最优解。

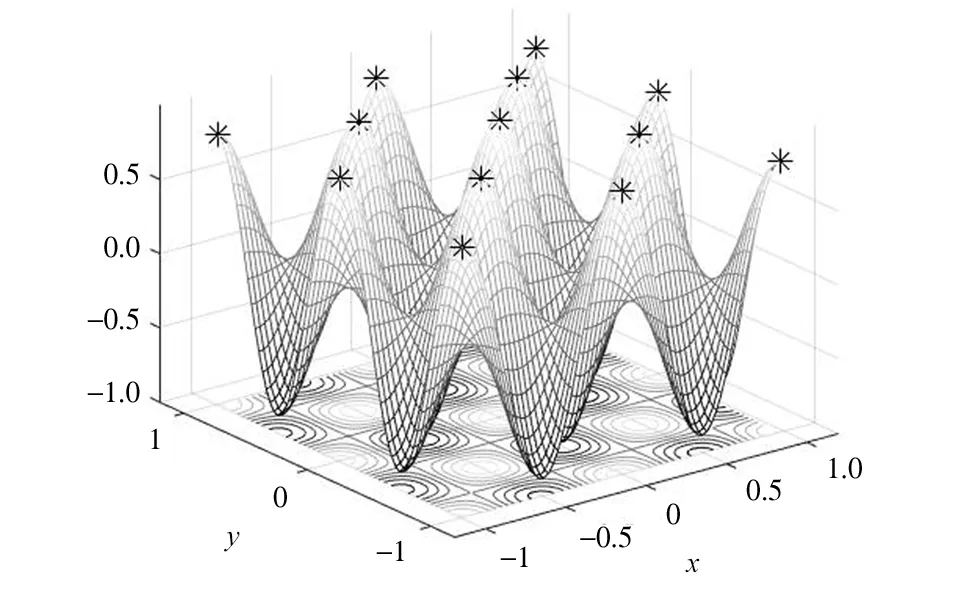
图2 小生境鱼群算法优化f1函数峰值分布图

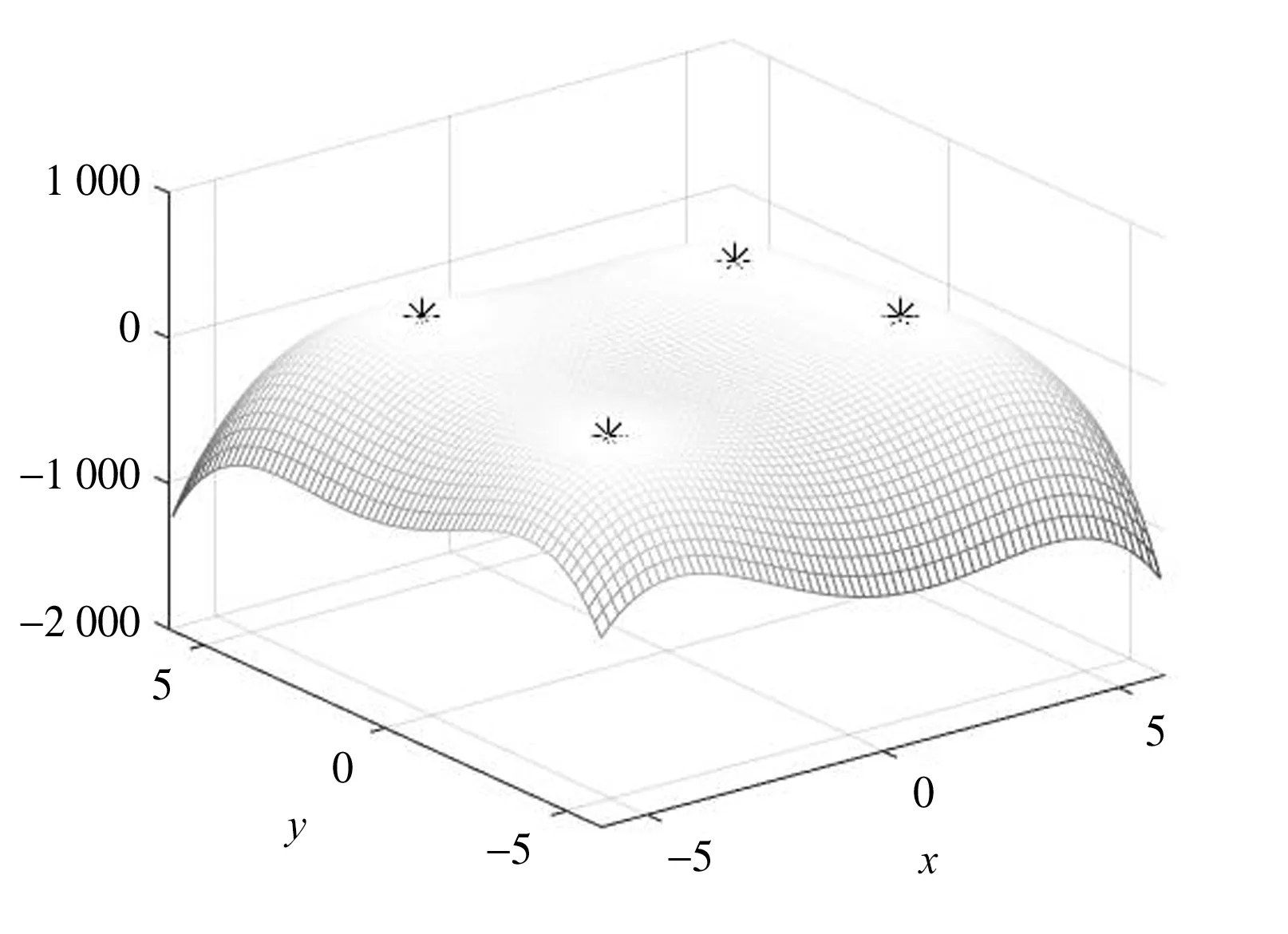
图3 小生境鱼群算法优化f2函数峰值分布图

3 缩尺斜拉桥有限元模型修正

3.1 缩尺斜拉桥实桥及有限元模型

缩尺斜拉桥原型为某长江大桥，结构形式为一座双塔三跨的斜拉桥，缩尺比例采用1∶40，模型总长18.20 m。桥跨布置为4.25 m+9.70 m+4.25 m，主塔采用钻石形，高3.46 m，拉锁为双面扇形，共56根。主梁材料采用弹性模量Ec=2.1×104MPa、密度ρc=2 400 kg /m3的轻质混凝土，主塔采用弹性模量Es=2.1×105MPa、密度ρs=7 850 kg/m3、厚4 mm的钢材，拉索采用抗拉强度为1 860 MPa的钢绞线。

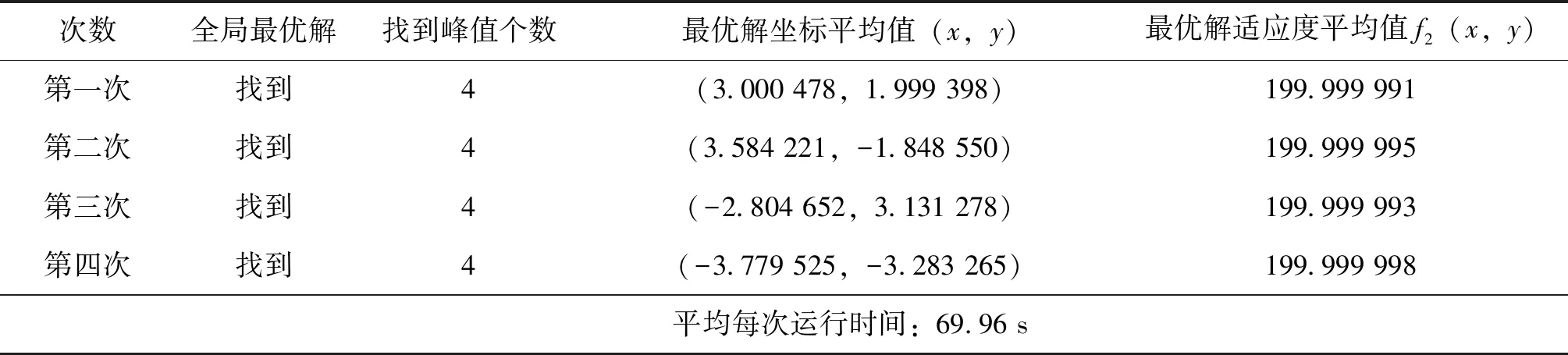
表3 小生境鱼群算法优化函数f2的统计结果

有限元模型采用可通过命令流调用程序的Ansys软件建立，模型中主梁与桥塔均采用实体单元solid45模拟，全桥共1 520个。拉索采用杆单元link10模拟，全桥共56个。边界条件设置为主梁两端一端竖向支撑、一端铰接，主塔底部固结，Ansys模型如图4所示。

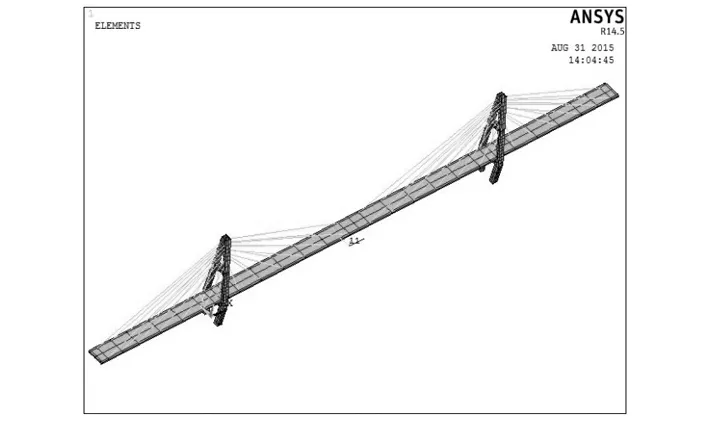
图4 缩尺斜拉桥Ansys模型

采用协方差驱动的随机子空间对该模型桥测试组2的测试结果进行模态识别，识别结果如图5；并根据Ansys有限元模型提取前6阶模态值，试验测试值与提取的结果如表4所示。

3.2 有限元模型修正

3.2.1 试验设计 根据相关研究结果[13-15]，初步选取对斜拉桥动力响应可能有较大影响的参数：主梁混凝土材料的弹性模量Ec及密度ρc、主塔弹性模量Es及密度ρs。4个参数的初始值分别为：2.1×104MPa、2.4×103kg/m3、2.1×105MPa、7.85×103kg/m3。考虑各参数交叉项及平方项共14个因素，采用拉丁超立方生成50组实验数据后对各因素进行F值检验，根据检验结果对前6阶频率影响显著水平满足P<0.05的参数进行回归分析，采用最小二乘法确定多项式系数，建立前6阶频率含交叉项多项式的响应面模型。各因素显著性分析结果如图6所示，前6阶频率响应面模型拟合系数如表5所示，其中A、B、C、D分别表示参数Ec、ρc、Es、ρs。

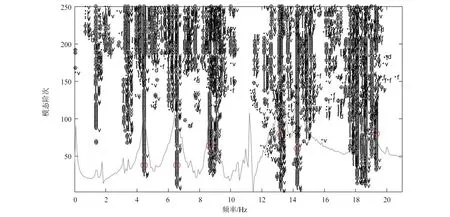
图5 测试组2随机振动响应识别的稳定图

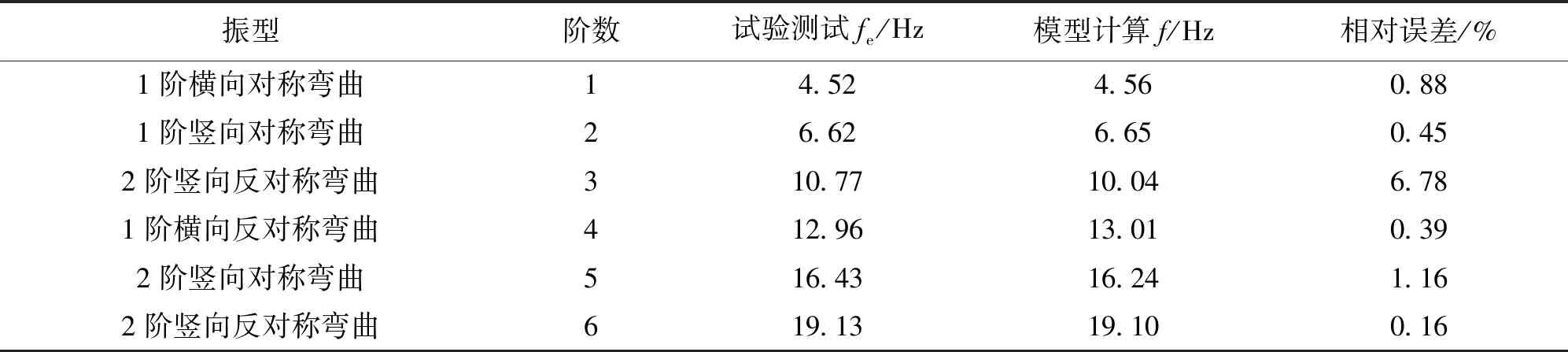
表4 模态实测值与有限元理论值的对比

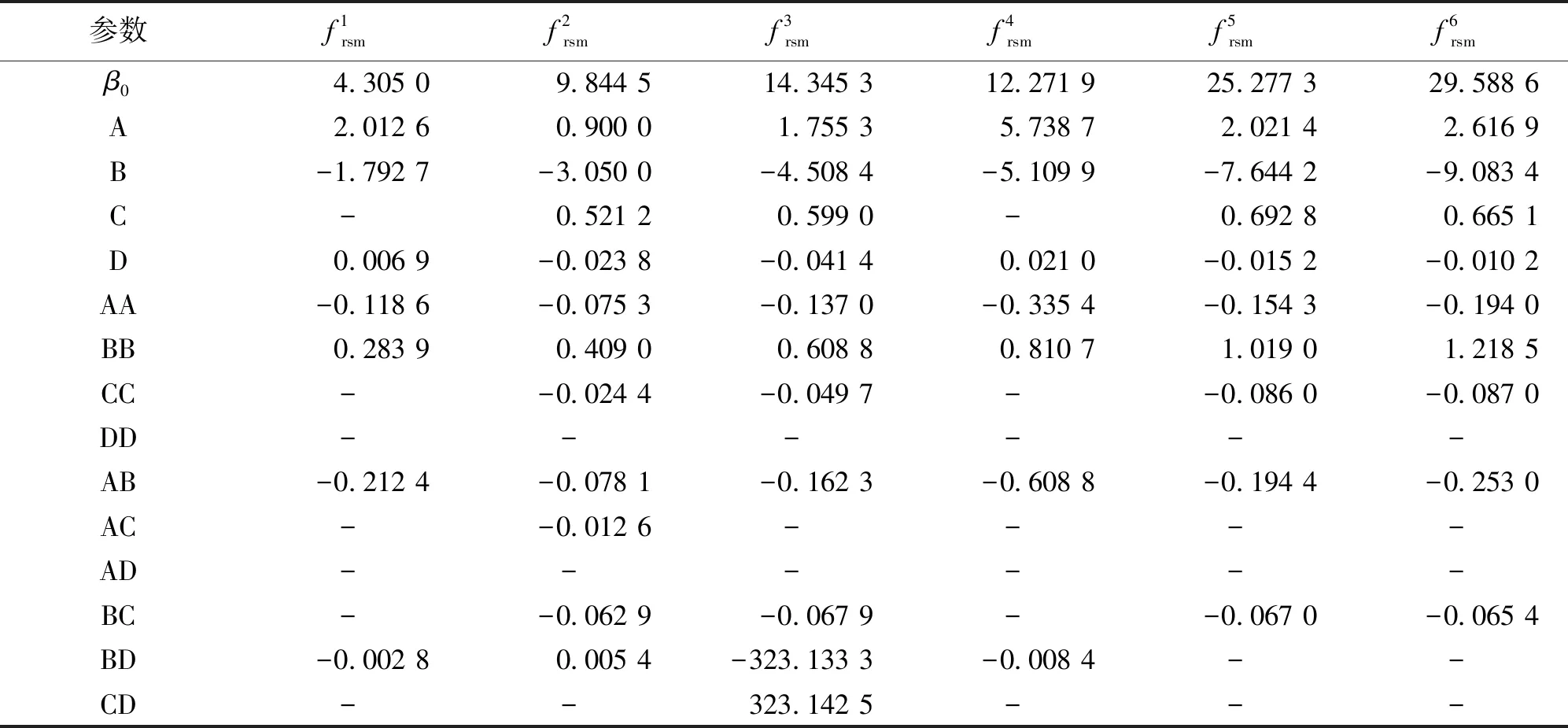
表5 各阶频率响应面模型拟合系数

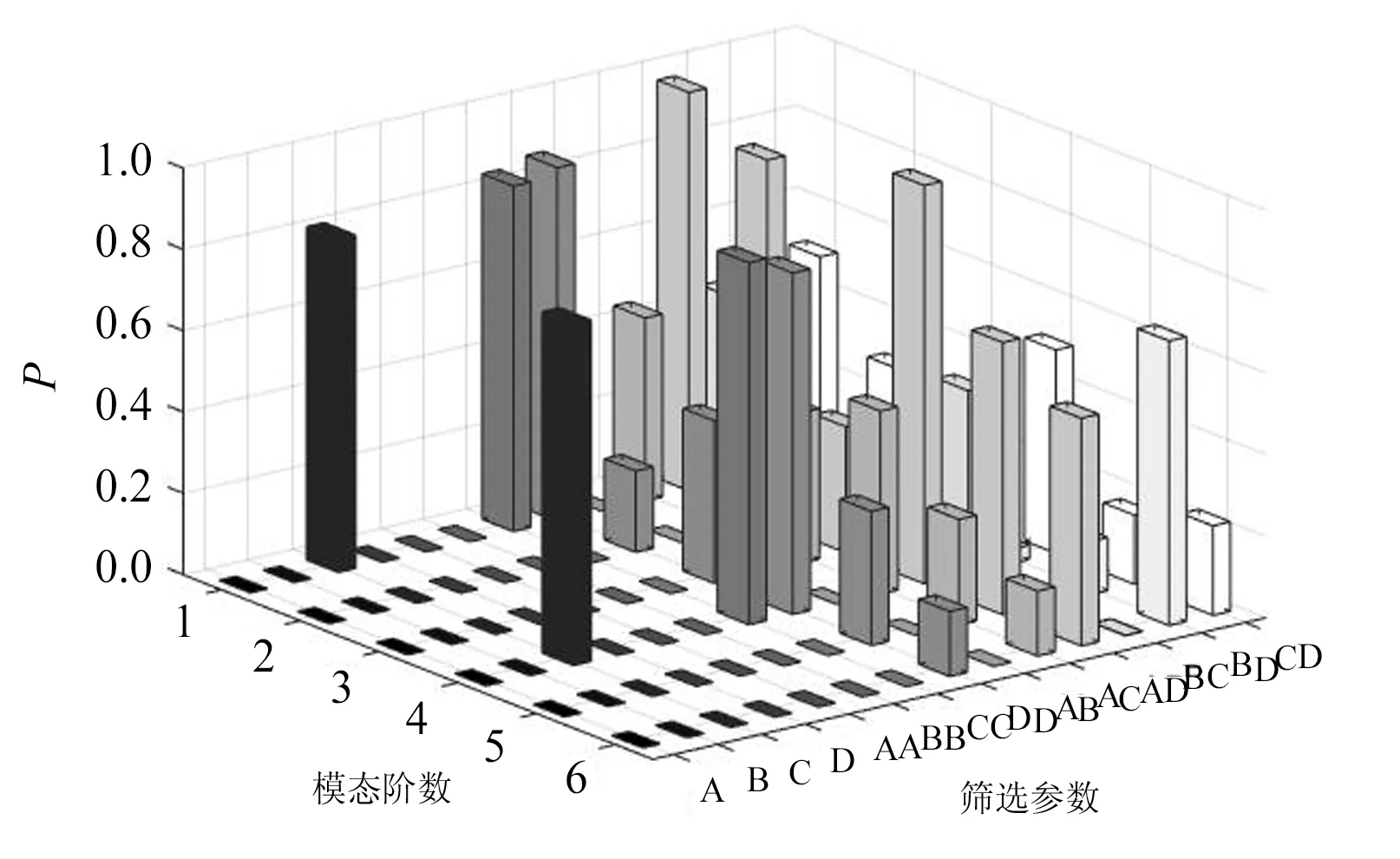
图6 14个因素的显著性P值

建立各阶模态的响应面模型后，对拟合精度进行检验，本文分别采用残差R2检验及均方根误差RMSE检验，各阶模态响应面模型R2、RMSE检验值如下表6所示。

由表6可得，各阶模态响应面模型的残差值保留4位小数后均为1，均方根误差值都在10-5数量级上，表明所建立的响应面模型能够精确地拟合各阶模态值。

3.2.2 模型修正 本文选取主梁混凝土及主塔钢材的弹性模量与密度共4个变量作为待修正参数，并设置这四个变量的区间范围为[x-x×0.4，x+x×0.4]。由Matlab调用小生境鱼群算法及各阶模态响应面模型，找到以模型理论值与实测值误差最小为目标函数的若干组全局最优解及局部最优解，目标函数的表达式如式(6)所示：

(6)

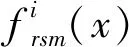
通过多次运行小生境鱼群算法优化目标函数参数值，当鱼群数目取值区间为[50,100]，最大迭代次数取值区间为[50,100]，视野取值区间为[2.0,6.0]，步距取值区间为[0.3,0.8]，拥挤因子取值区间为[0.1,0.6]，小生境半径按式(6)取值区间为[0.58,1.75]，模拟退火算法初始温度T0=200 0 ℃，终止温度Tend=0.01 ℃，各温度下的迭代次数L=200，目标函数可得到较优解集。

特殊地，小生境鱼群算法参数设置如下：鱼群规模为N=50，最大迭代代数gen=100，鱼群视野范围为2.12，步距为0.40，拥挤因子设为0.218，小生境半径设置为0.8；模拟退火算法初始温度T0=200 0 ℃，终止温度Tend=0.01 ℃，各温度下的迭代次数为200次。经迭代计算，得到1组全局最优解及7组局部最优解，并将优化所得到的参数值分别代入有限元模型中提取前6阶模态值。限于篇幅，本文仅列出1组全局最优解与3组局部最优解，模型修正前后参数取值变化如表7所示，全局最优解及局部最优解对应参数下的模态理论计算值与实测值如表8所示。

表6 各阶模态R2及RMSE的检验值

表7 修正前后的材料参数值对比

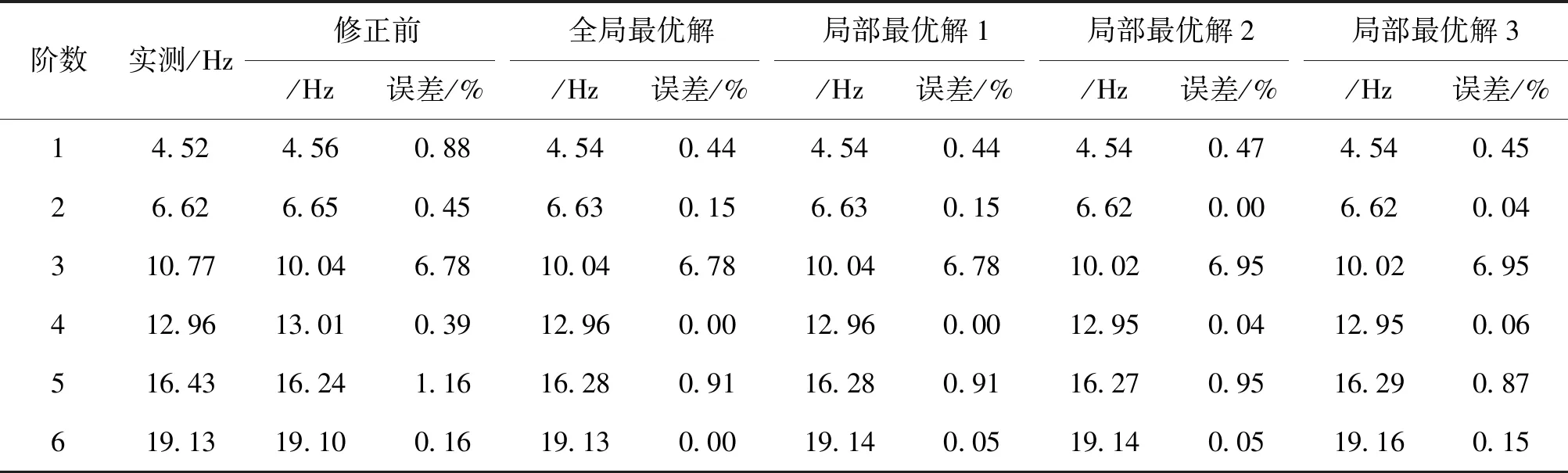
表8 修正后计算模态值与实测值误差

由表8可以看出，采用全局最优解所得参数值代入有限元模型后理论频率与实测频率的误差在第1、2、4、5、6阶模态均有减少，且第4、6阶模态的误差下降为0%，第3阶模态误差值与修正之前相同。全局最优解参数变化最大的为主塔材料，其弹性模量相对初值减少20.0%，密度减少36.3%，而主梁所采用的混凝土材料的弹性模量相对初值增大11.9%，密度减少1.2%。3组局部最优解代入有限元模型后理论频率与实测频率的误差在第1、2、4、5、6阶模态均有减少，但对第3阶模态值修正空间不大。虽然局部最优解与全局最优解各维参数值有所差异，但均能够有效减少模态理论计算值与实测值的误差，能够为工程决策者提供更多选择方案，减少对结构真实参数取值误判的可能。

小生境鱼群算法与AFSA算法优化目标函数的全局最优解迭代过程如图7所示，两者分别收敛到0.083与0.085，表明后期采用模拟退火的小生境鱼群算法收敛精度比AFSA精度高。

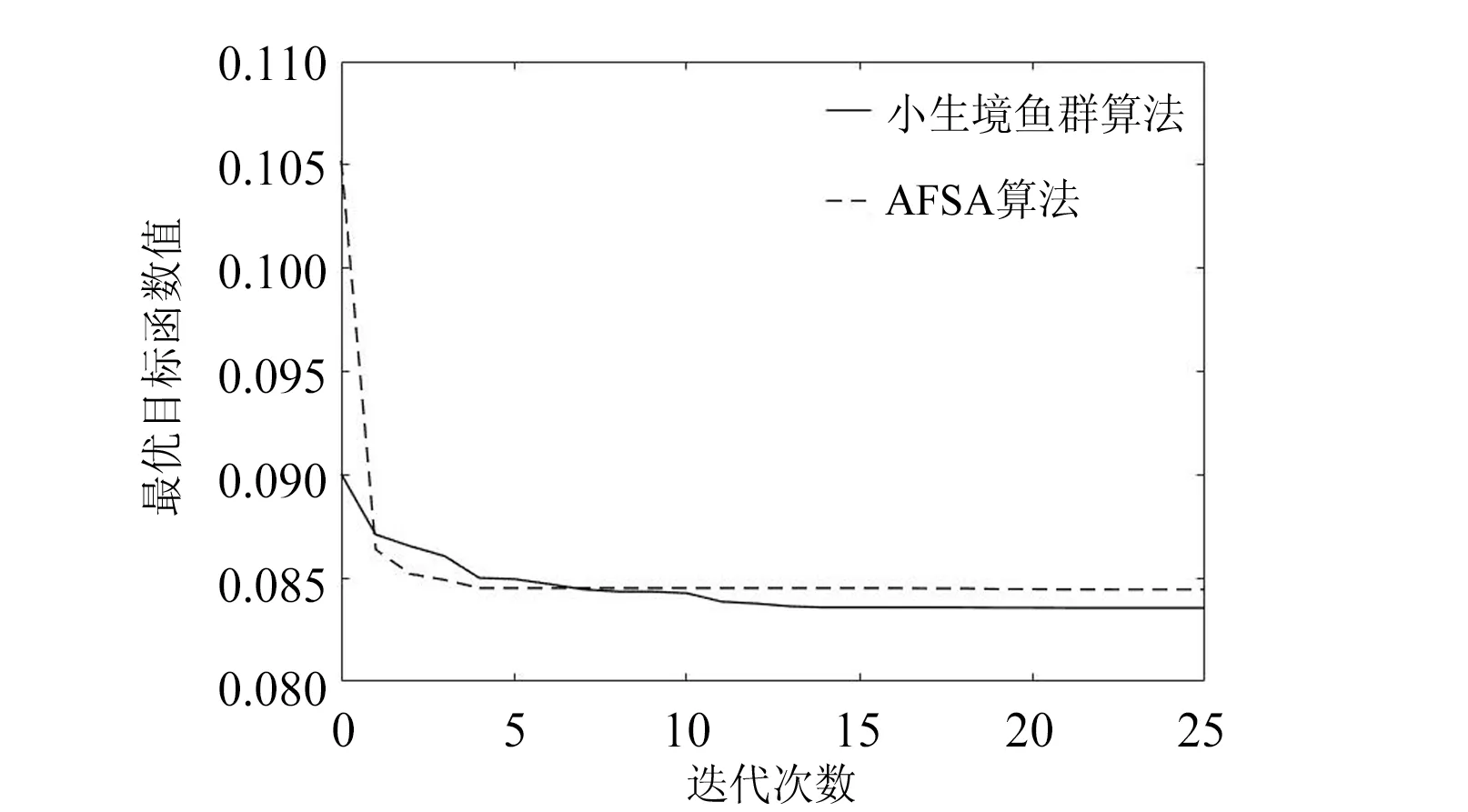
图7 小生境鱼群算法及AFSA算法优化目标函数收敛曲线

4 结 论

1)提出一种改进的小生境鱼群算法，该算法引入了小生境技术、反向学习策略、并在算法后期采用模拟退火算法局部细化寻优，文中给出3个典型的函数测试小生境鱼群算法的性能，验证了小生境鱼群算法能够精确、快速找到多峰值函数多个峰值的功能。

2)采用拉丁超立方生成实验数据，并通过F值检验，剔除影响不显著因素，建立缩尺斜拉桥以前6阶模态为输出对象的响应面模型，并对各阶模态响应面模型采用R2及RMSE检验其准确度。检验结果表明，采用含有二次交叉项的各阶响应面模型残差值均为1(保留4位小数后取值)，均方根误差数量级均为10-5，表明所建立的响应面模型能够精确地代表有限元模型。

3)与传统有限元模型修正不同，本文将所提的小生境鱼群算法应用在一座缩尺斜拉桥有限元模型修正中，得到1组全局最优解及7组局部最优解。全局最优解及局部最优解对应的参数取值均有效减少了缩尺斜拉桥在第1、2、4、5、6阶模态理论值与试验测试值间的误差。并认为由于传感器数量有限，所测量数据不充分以及测试过程中仪器识别可能存在误差等原因的存在，局部最优解可能比全局最优解更能代表结构实际参数，为决策者提供了更多的选择方案。因此，决策者可根据工程经验对多组解做出进一步判断，例如：缩尺桥梁构件在制作过程中的材料性能实际值与理论值的可能误差范围；结合缩尺桥梁的静力特征验证各组解；通过对缩尺桥梁进行外观检测，根据详细病害确定各构件可能会发生的材料性能变化等，以减少对结构实际参数误判的可能性。