基于双层规划的共享自行车区域投放规划模型*
2020-04-16胡郁葱黎俊廷陈枝伟
胡郁葱 ,黎俊廷 ,陈枝伟
(1.华南理工大学土木与交通学院,广东 广州 510640;2.现代城市交通技术江苏高校协同创新中心,江苏 南京 210096;3.南佛罗里达大学土木与环境工程学院,美国 坦帕 33620)
共享经济为绿色出行、可持续发展提供了重要的实现路径。作为共享经济的产物,共享自行车以低碳环保、资金和基础设施投入少、便民惠利等优势,成为居民短距离出行的主要交通方式之一。但许多地区出现了共享自行车投放与用户需求不平衡的现象,如何在合适的投放区域投放适量的车辆成为共享自行车企业需要解决的问题。
与公共自行车[1-3]不同的是共享自行车没有固定的站点,共享自行车的投放一般是根据客流的分布情况将车辆投放在小区、商圈、写字楼周边。由于共享自行车投放点难以确定,目前大多数的研究聚焦于共享自行车的调度以及投放量的预测[4-8]这两方面。Leonardo等提出了一种动态共享自行车调度的方法,以尽量满足用户需求、降低调度成本为目标,实现共享自行车的调度[9]。在共享自行车投放量预测方面,周传钰构建了以轨道交通站点为中心的区域投放点布局模型,并结合轨道交通客流数据探讨了共享自行车投放量的测算方法[10]。夏芸等以人口密度、人均可支配收入和公交站点密度为指标,计算指标信息熵值和信息效用值,进而对共享单车需求进行评估[11]。索源以系统总成本为目标函数,建立考虑出行需求波动的共享自行车停放点投放量鲁棒规划模型[12]。
目前对于共享自行车投放点选址及规模的研究已有不少,但是上述研究都分别从成本利润或者用户需求出发,大多没有同时考虑系统总成本、用户出行成本以及用户出行需求来规划共享自行车投放的位置以及数量。针对上述问题,本文综合考虑企业投资总成本、用户出行时间成本以及出行需求,构建共享自行车区域投放双层规划模型,并利用某中等城市中心区共享自行车出行数据验证模型的有效性。
1 共享自行车网络系统
为了方便共享自行车区域投放的选址,本文假设每一共享自行车投放区域有一个虚拟的投放点,如图1所示,该点的投放量是这一区域共享自行车投放量的总和。通过调查得到用户可接受的步行距离,以此距离作为半径确定区域范围进行车辆投放。我们通过确定虚拟投放点的位置以及投放量后,再根据投放点周边的实际情况灵活地确定共享自行车的投放位置,因此可以将共享自行车投放点选择问题转化为对虚拟站点的选址以及规模的研究。

1.1 共享自行车出行过程
共享自行车出行是指用户使用共享自行车从起点到终点的单向出行过程,共包括5个阶段:① 从起点交通小区r步行至借车点m;② 在借车点m借车;③ 使用共享自行车从借车点m骑行至另一还车点n;④ 在还车点n还车;⑤ 从还车点n步行至终点交通小区s。用户使用共享自行车出行的成本包括步行时间成本和骑行时间成本,以及租赁费用对应的时间成本。因此,OD对(r,s)第k条出行路径的出行时间为:
(1)

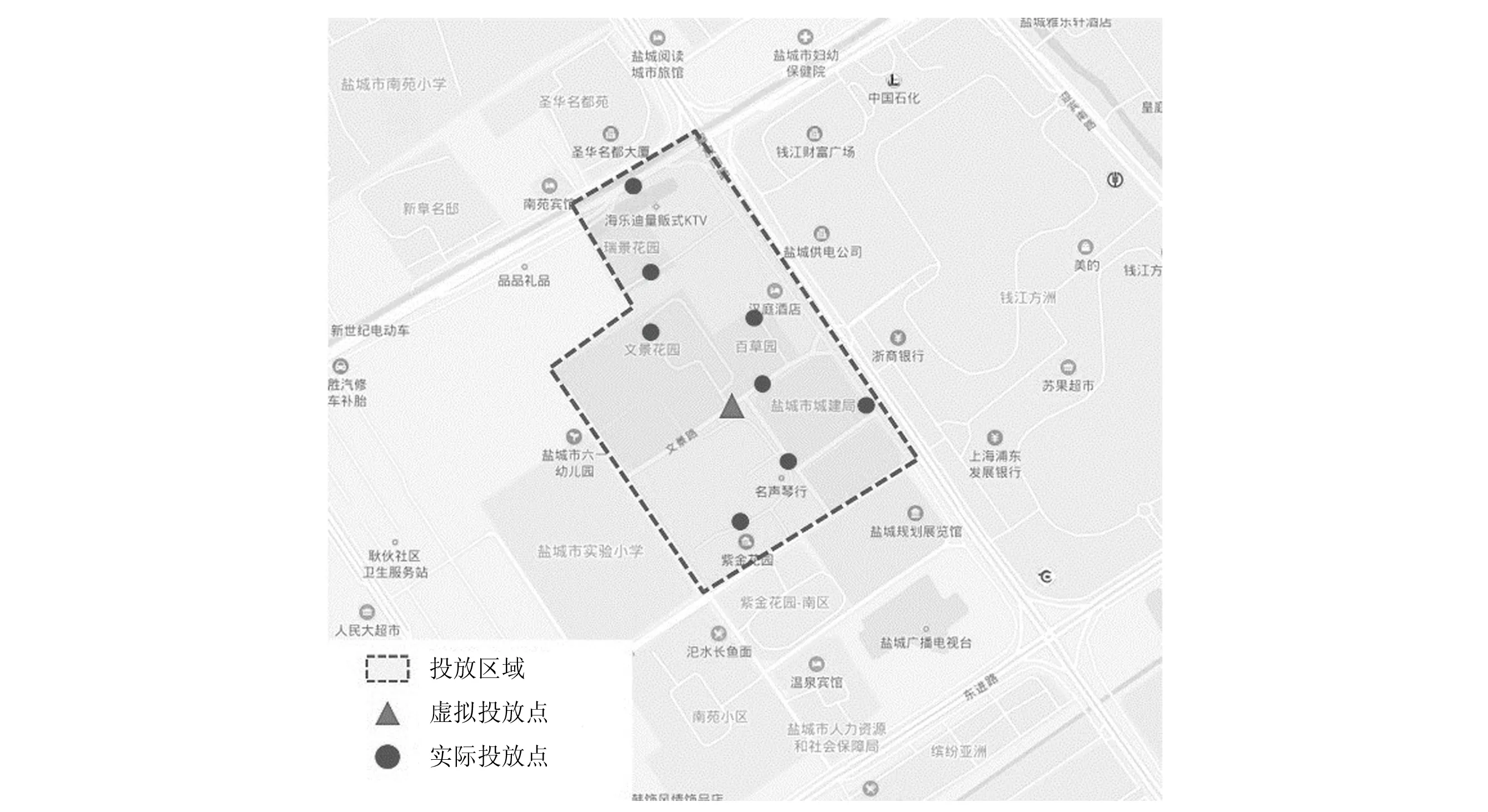
图1 投放区域虚拟投放点示意图

(2)
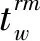
1.2 步行时间
步行时间是指用户从起点交通小区r步行至借车点m或从还车点n步行至终点交通小区s所花费的时间。假设交通小区出行需求均匀分布,当小区面积不大时,可以将交通小区的需求或吸引最集中的点视作该小区的需求或吸引发生点。步行过程是指从小区需求发生点至借车点以及还车点至小区吸引发生点的过程,则步行时间可表达为:

(3)
式中,srm、sns分别为起点r至借车点m和还车点n至终点s的距离;vw是平均步行速度。
1.3 广义骑行时间
骑行时间为用户从借车点m骑行共享自行车到还车点n的时间,骑行时间与借还点距离以及路段流量有关。Jin等对在中国杭州采集的电动自行车和自行车混合流数据进行拟合,得到了8个交通流基本图,并证明了混合自行车流特性与机动车流的特性存在一定相似性[13],所以可以参照传统的交通流模型来分析文中的自行车交通流。参照Greenshields模型对自行车流进行分析,可以得到共享自行车路段车速与流量之间的关系。而且,通过实际生活中的观察可以知道共享自行车流密度大部分情况下都小于堵塞密度,所以文中暂时只考虑共享自行车流密度小于或等于堵塞密度的情况,此时vmn≤vf/2。若自行车获得独立路权行驶,则其在借车点m和还车点n之间的骑行时间为:
(4)
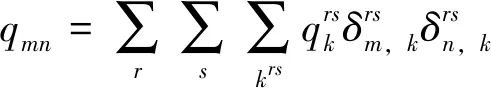
(5)
式中,vf是在自由流状态下借车点m和还车点n之间的共享自行车的速度;kj是借车点m和还车点n之间的共享自行车阻塞密度;qmn为m和n之间的共享自行车流量;smn是借车点m和还车点n之间的距离;vmn是借车点m和还车点n之间的共享自行车行驶速度。
实际上,很多城市没有设置自行车专用道,因此引入速度折减系数得到修正后的骑行时间公式为:
(6)
式中,ξ为速度折减系数,若设置了共享自行车专用道ξ=1,否则0<ξ<1。给定共享自行车的单位租赁费用c与时间价值成本τ,就可以利用用户在借车点和还车点之间的骑行时间计算出租赁费用。将与租赁费用等值的时间加到骑行时间中,得到广义骑行时间为[14]:
(7)
2 共享自行车区域投放选址布局模型
2.1 假设条件
共享自行车区域投放选址布局模型假设条件如下:
(1)将一个交通小区划分为多个区域,模型中的投放点为区域投放的虚拟投放点,该点的投放量是这一区域投放量的总和。
(2)共享自行车流是单向的,即总是从借车点到还车点。任意投放点都具备借车和还车功能,视其在出行路径中的位置而定。
(3)各交通小区的需求或吸引发生点是该小区共享自行车发生量和吸引量最集中的点,但是该点并不一定是小区的形心。不考虑小区内的交通出行,各小区的需求量是根据数据获得的需求量,因此本模型是一个确定需求条件下的静态模型。
2.2 双层规划模型
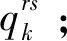
上层模型以系统用户总的出行成本最小为目标,考虑了企业、用户和参数取值域约束三类约束条件;
(8)
(9)
(10)
s.t.
(11)
(12)
(13)
(14)
(15)
(16)
(17)
bx≤Myx,∀x∈X
(18)
bx∈N+,∀x∈X
(19)
yx∈{0,1}
(20)
(21)
企业在建设共享自行车系统时主要考虑的因素是投资总成本以及运营成本。式(11)、(12)分别为共享自行车系统的投资成本和运营成本,bx为区域x内投放的共享自行车数量,cb为共享自行车单价,Cf为共享自行车系统建设资金上限。co为区域投放点的运营费用,包括共享自行车在区域内调度的费用、人工成本以及维修费用等。Cv为系统运营资金的上限。
出行者在共享自行车网络中的分布情况会对投放点的布局产生决定性的影响,因此投放点的布局方案应该尽量与网络内的共享自行车流量分布相适应[15]。均衡模型的原理是出行者会选择最短的路径出行,最终被利用的所有道路行程时间相等,达到均衡的状态[16]。根据Wardrop第一原理,假设选择共享自行车出行的用户都确切知道网络的交通状态并试图选择最短路径,共享自行车出行网络将会达到平衡的状态,因此,下层模型中我们选用网络流量均衡模型来分析共享自行车在网络中的均衡分配情况[17]。
qrm,qns,qmn,qx∈argminZ2=Z21+Z22
(22)
s.t.
(23)
(24)
(25)
(26)
(27)
(28)
qx≤Myx,∀x∈X
(29)
qmn≤Mymn,∀m,n∈X
(30)
0≤qrm≤Mym,∀m∈X
(31)
0≤qns≤Myn,∀n∈X
(32)
网络均衡模型中的目标函数形式为对路网中所有路段流量的积分求和,这里也采用了这种形式。步行时间受行人流量的影响较小,所以该积分等于求共享自行车网络中步行时间总和,得到目标函数的第一部分Z21。
(33)
如式(7)所示,与传统的城市交通流网络均衡模型不同[18],本文将共享自行车用户在路网中的时间扩展为综合考虑了时间成本和租赁费用的广义骑行时间;式(24)为广义骑行时间对路段流量的积分求和,得到目标函数的第二部分Z22。
式(25)为流量守恒约束;式(26)为流量非负约束;式(27)、(28)计算站点以及路径流量;式(29)约束了只有选中的投放点才能分配共享自行车。式(30)表示只能在两个选中建设的共享站点之间分配流量,式(31)、(32)表示只能够在交通小区和选中建设的共享站点之间分配流量。
2.3 模型求解算法
我们利用下层模型的一阶条件(34)-(37),将双层规划模型转化为单层模型,下层模型的一阶条件就是共享自行车网络流量均衡条件,所以对一阶条件进行求解就能获得共享自行车共享网络的流量均衡解[19]。
(34)
(35)
(36)
(37)
式中:urs为OD对(r,s)之间的最短出行时间。目前导致一阶条件在实践中难以应用的原因之一是其非凸性,为了解决这个问题,我们引入0-1变量将其转化为线性等式约束:
(38)
(39)
(40)
(41)
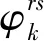

(2)采用拉格朗日乘子法将模型转化为无约束的非线性规划模型,代入计算后得到每个粒子的适应度值。
(3)将粒子的适应度与个体极值pb(i,:)进行对比,如果适应度大于个体极值,将个体极值替换为适应度值。
(4)将每个粒子的适应度值和全局极值gb进行对比,如果适应度大于全局极值,将全局极值替换为适应度值。


(42)
(6)如果满足结束条件(误差足够低或者达到最大循环册数)则退出,否则返回步骤(2),进行循环迭代。

bx=qx/φbike
(43)
3 案例分析
3.1 案例背景
以某市两个区为例进行分析,收集2015年1月到8月的共享自行车出行数据,包含有共享自行车出行借还点位置的出行记录。以此数据作为区域内的自行车出行需求数据,假设需求不变,进行建模研究。
为了将共享自行车借还点位置数据代入到模型中,本文通过kmeans聚类方法将相邻的借还点位置进行聚类,得到73个借还分布密集的点,这些点附近的共享自行车借还需求量较大,满足作为区域投放备选虚拟投放点的要求。以城市主次干路作为边界并根据区域的用地性质,将研究区域划分为22个半径约为0.5 km的交通小区,不考虑交通小区内部的共享自行车出行。交通小区划分及备选投放点分布情况如图2所示。利用python对共享自行车借还记录进行处理,得到各交通小区之间的共享自行车出行需求量。交通小区间的期望线如图3所示,可以看出其中某几个小区之间交通需求较大。同时,通过地图软件获取小区需求吸引发生点到各个投放点以及各个投放点之间的距离。
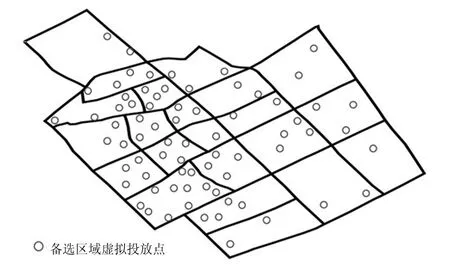
图2 交通小区划分及备选投放点分布

图3 交通小区期望线图
案例计算中,选取的系统运营参数如表1所示。
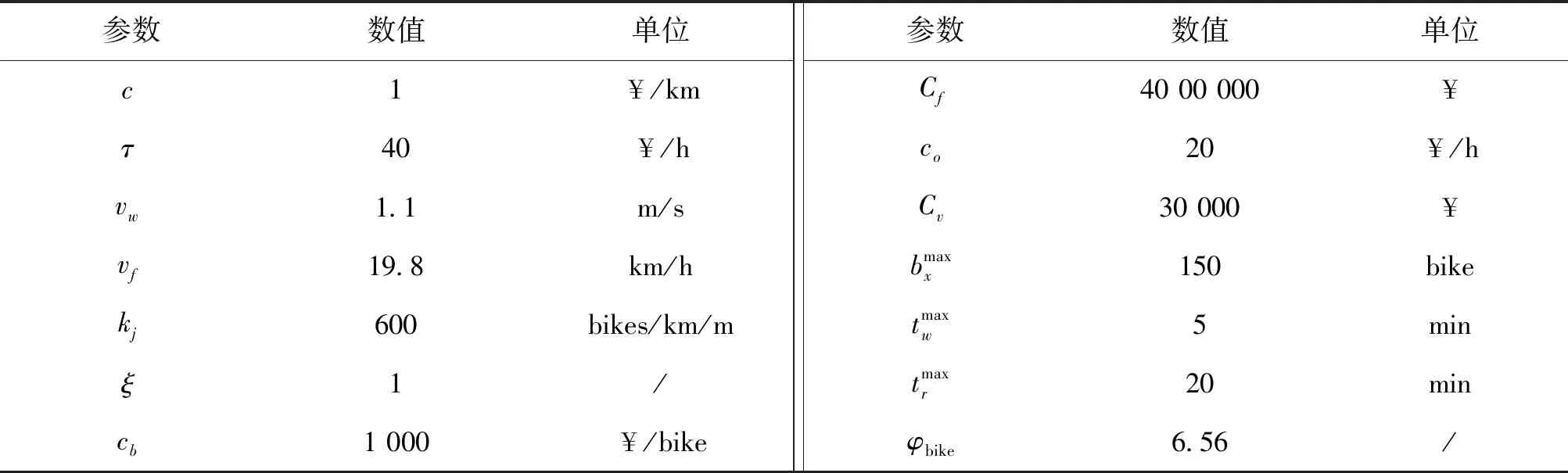
表1 系统运营参数表(1.0倍需求情况下)
3.2 结果分析
在一台装有Windows7.0(专业版)系统的电脑上采用Matlab2014a语言实现2.3中的算法,相关算法参数取值如下:bn=10、rn=4、sn=3、z=10、g=0.5、lf1=2、lf2=2、ε=0.08。
通过运行,得到选中的虚拟投放点以及在这些点周边投放的共享自行车数量,如图4所示。图4中,从备选投放点中选中40个投放点,在投放点周边投放共享自行车共2 558辆。从图4以及图5中可以看出,中心区商圈、写字楼、学校等人流密集的区域交通需求较为聚集,选中的投放点相对比较密集且投放量较多;而远离中心区的区域交通需求量小,选中的投放点以及投放量较少。
为了研究不同交通需求情景下的投放点布局情况,我们通过改变小区间的出行需求量,分别研究了0.5/1.0/2.0/3.0倍需求情景下的投放点分布及投放量的变化情况,如图6(a)-(d)及表2所示。从结果可以看出,随着交通需求量的增加,需要投入的共享自行车数量也随之增加,虚拟投放点的数量增多,同时有向中心区聚集的趋势。这是因为高需求的情况下,中心区的客流吸引力变大,靠近中心区的共享自行车需求量增加,与实际情况较为相符。
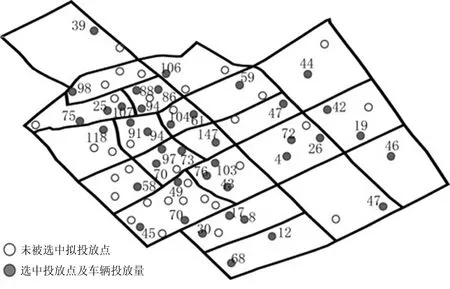
图4 选中的投放点分布及投放点投放量
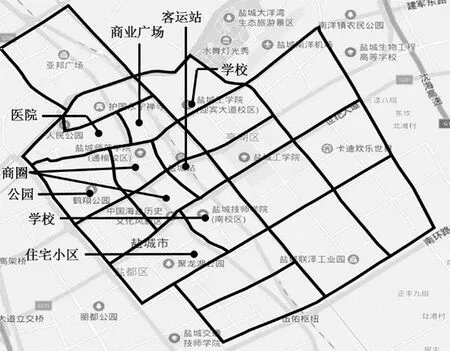
图5 主要客流聚集点示意图

图6 0.5/1.0/2.0/3.0倍需求情景下的投放点分布及投放量
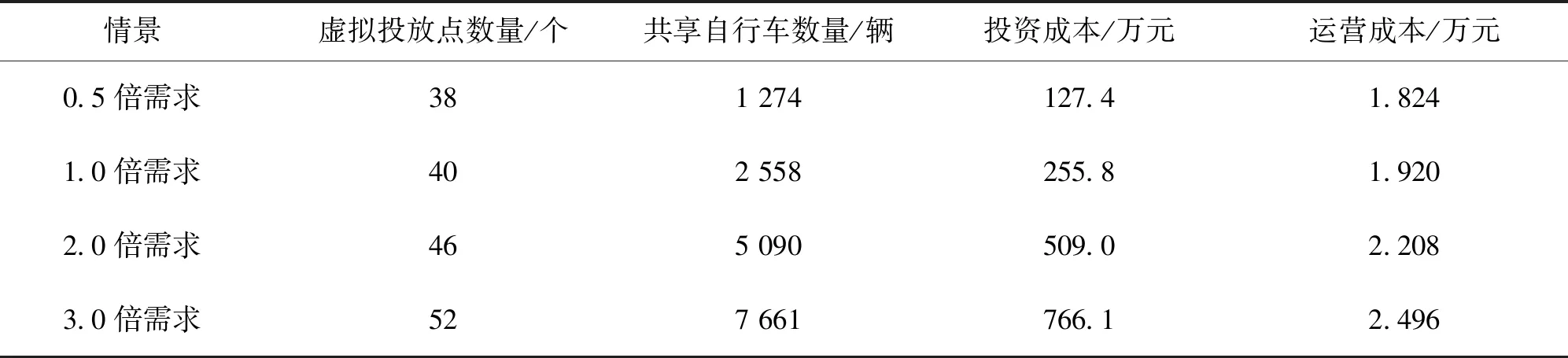
表2 不同需求情景下的投放点及投放量
与1.0倍需求相比,在2.0、3.0倍需求情况下,投放点数量增加了15%、30%,运营成本增幅与投放点一致,共享自行车数量增加了98.98%、199.49%,投资成本增幅与共享自行车数量一致。结果表明,当需求量呈倍数增长时,投放的自行车以及投资成本也呈倍数增长,投放点数量和运营的成本增幅较小。当需求倍数较小时,为了保证共享自行车的覆盖范围,需要一定数量的投放点。因此需求倍数增长时,投放点数量增幅较小,运营成本由投放点数量决定,增幅与投放点一致。而共享自行车数量与需求倍数有关,所以随着需求倍数的增加而增加;投资成本由共享自行车数量决定,所以增幅与共享自行车一致。
为了研究四种需求情景下的出行时间、用户步行距离以及骑行距离的变化情况,我们从结果中获取了不同需求情景下的用户从起点到终点的平均出行时间、平均步行距离以及平均骑行距离进行比较分析(图7-9所示)。从图7中可以看到,用户平均出行时间与出行需求呈递增的关系,原因是路段上共享自行车的流量随着需求的增加而增加,导致车速变低,骑行时间变长,用户平均出行时间增加。

图7 不同需求情形下的用户平均出行时间
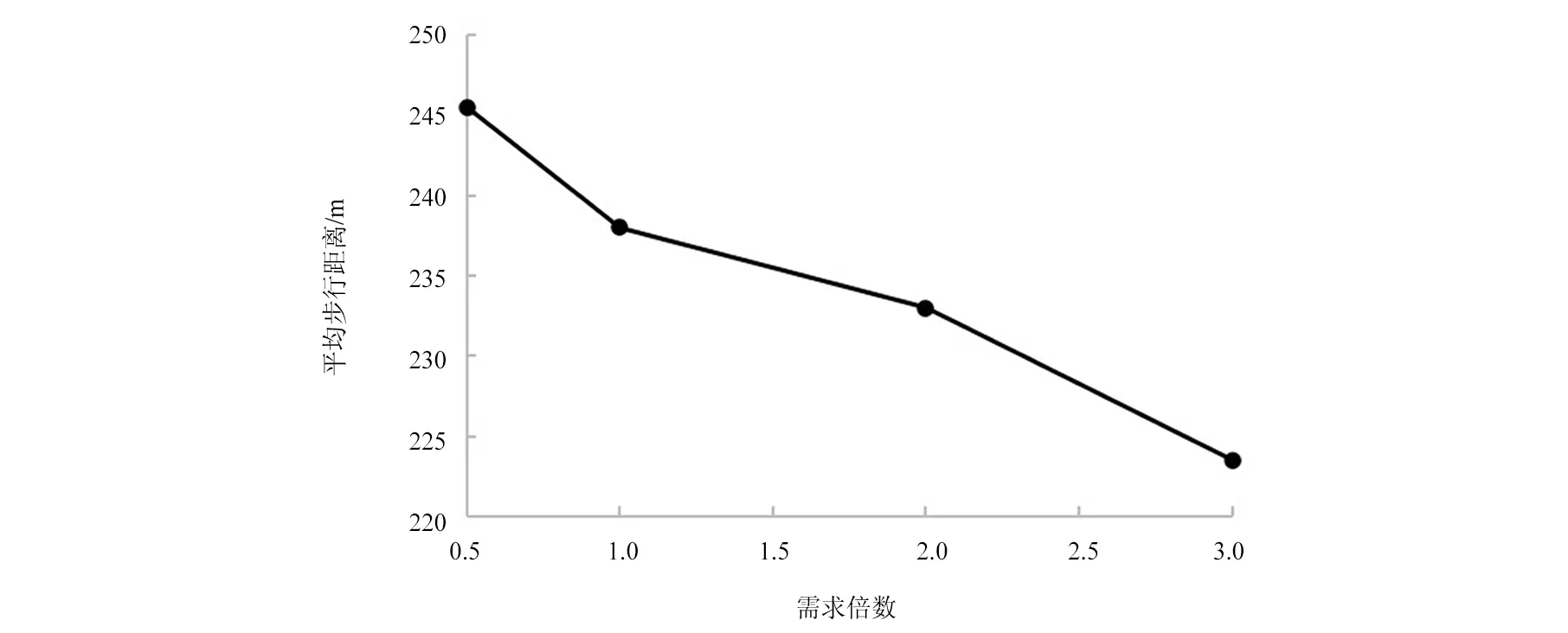
图8 不同需求情形下的用户平均步行距离
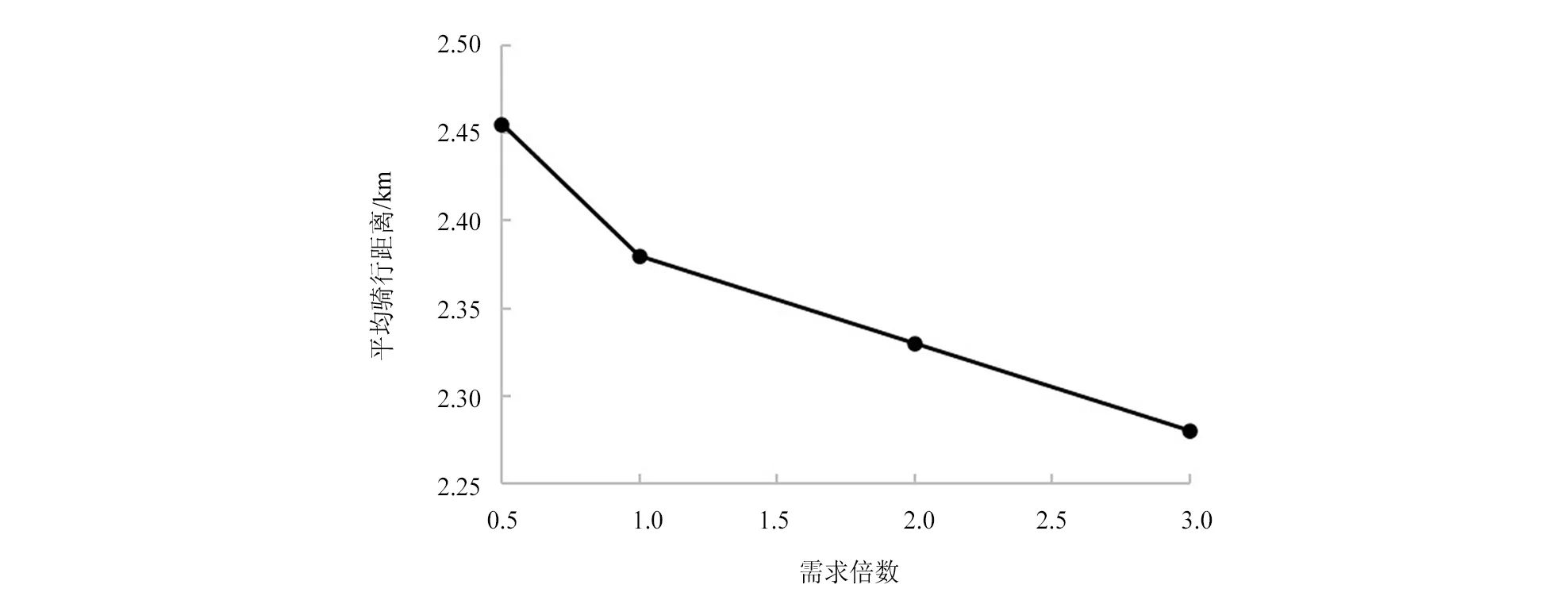
图9 不同需求情形下的用户平均骑行距离
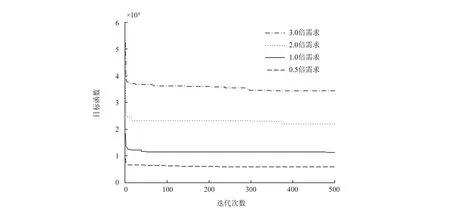
图10 算法迭代收敛性
从图8以及图9中可以看出,用户平均步行距离、平均骑行距离与出行需求呈递减的关系。我们认为可能是因为随着需求的增加,选中投放的虚拟站点增加,交通小区内的用户可以在离起终点更为相近的投放点周边进行借车或还车。同时,交通小区之间有更多的路径可供选择,能够选择骑行距离更短的路径。从图6观察到,高需求情境下选择投放的站点有向中心区聚集的趋势,中心区客流密度较大,选中投放的站点越多,用户平均步行距离以及骑行距离越小。虽然投放点的量增加不多,但自行车的投放总量增加了,表明模型倾向于选择使用大容量站点从而降低站点数量,而并非增加站点数量而减小站点容量。本模型考虑到了路段上共享自行车流量与速度的关系,因此在高需求的情景下,尽管平均出行距离变短,用户的出行时间还是有所增加。此外不难看出,随着投入的虚拟站点以及共享自行车的增加,用户使用该系统出行会变得更加便捷,但这随之而来的是投入成本的增加。
比较四种不同需求情景下的迭代次数与目标函数之间的关系,如图10所示。四次实验表明,该算法在迭代500次内均可收敛,平均运行时间为1 737 s。因此,可以认为该算法收敛性能好,收敛速度快。
4 结 论
本文针对共享自行车乱停乱放以及投放与用户需求不匹配的问题,提出了共享自行车区域投放的选址布局双层规划模型。模型上层以系统用户总的出行成本最小为目标,在考虑企业成本、用户需求等约束的前提下,设计合理的投放点布局,使得共享自行车出行达到系统最优;模型下层则采用用户均衡模型来描述共享自行车用户出行行为;并提出混合遗传算法与粒子群算法的求解算法。最后,以某中等城市的共享自行车出行数据为例进行建模分析,算例结果表明该算法能够同时确定投放区域的选址及规模。并且通过改变小区间的出行需求量研究了不同交通需求情景下的投放区域布局情况,结果显示:随着需求量的增加,共享自行车虚拟投放点有向中心区聚集的趋势,反映了高需求情况下中心区的客流吸引力变大的情况。经过分析不同需求情景下用户出行时间、步行距离以及骑行距离的变化,可以知道,随着投入的虚拟站点以及共享自行车的增加,用户使用该系统出行会变得更加便捷,但这伴随着投入成本的增加。
