基于电流初始行波极性的主动配电网纵联保护方案

许名扬，樊艳芳，刘群杰，罗 瑞

（1.新疆大学 电气工程学院，新疆 乌鲁木齐 830047； 2.国网河南省电力公司 周口供电公司，河南 周口466000）

0 前言

大规模分布式电源 （Distributed Generation，DG）接入主动配电网后，改变了配电网原有的潮流分布，可能使传统配电网三段式电流保护失去选择性[1]，[2]。 当线路发生单相接地故障时，可能造成电流保护的误动或拒动，严重影响主动配电网的供电可靠性[3]～[5]。

针对此问题，文献[6]考虑了DG 接入容量对配电网继电保护的影响，并提出加装基于电流和电压信息的方向元件来提高DG 的接入容量，但是在配电网线路上，一般不装设电压互感器。 文献[7]对DG 接入的配电网提出了自适应保护方法，并提高了电流保护的灵敏度，但由于缺少方向判定元件，易造成配电网中电流双向流动引起的保护误判。 文献[8]提出基于故障分量电流幅值比较的判别方法，但同一条母线上两条线路距离较近或故障点距离母线较近时，两条线路电流幅值接近，可能造成保护设备误动。 文献[9]提出基于多种群遗传算法的配电网故障定位方案，能够适应DG 的投切及结构复杂的配电网，但是在求解的过程中存在收敛问题，可靠性较低，无法准确定位故障区段。

本文基于主动配电网先进的传感通信技术、电流行波极性保护的快速性和不需要方向元件的优势[10]，提出一种基于电流初始行波极性的主动配电网纵联保护方案。 该方案通过判别故障初始行波到达线路两端时产生的暂态电流行波的极性来确定故障区域，并采用小波变换提取故障电流行波极性，以提高保护动作的灵敏性与可靠性。该方案不需要电压信息，且受中性点接地方式、故障位置、 过渡电阻和分布式电源投切的影响相对较小，符合保护安全性可靠性的要求。

1 电流行波极性比较式纵联保护原理

1.1 DG接入对主动配电网保护的影响

主动配电网系统在DG 接入后，系统由单侧电源系统变为双侧或多侧电源供电系统。 拓扑结构发生变化，故障电流的方向和幅值发生变化，可能对原有的无方向、 上下级线路相配合的传统电流保护造成误动和拒动的影响。 典型的DG 接入的主动配电网系统结构如图1 所示。

图1 DG 接入的主动配电网系统Fig.1 DG access to active distribution network system

当DG 接入的线路上游F1 处发生故障时，DG 提供的短路电流流过线路NK 可能使保护K3误动作。 当DG 接入的线路下游F2 发生故障时，DG 对下游线路的短路电流起到助增的作用，保护K5 处检测到的故障电流IK5将增大，且随着DG 的接入容量增加而增大，IK5有可能大于电流保护 I 段整定值，保护 K5 电流 I 段保护范围将会超过线路全长，造成保护K5 误动。 DG 的接入会对上游线路起到分流的作用，保护K3 处检测到的故障电流IK3减小，过电流灵敏度将明显降低。 此时，如果K5 速断电流保护故障，保护K3将拒动，故障无法隔离。 此外，当相邻线路F3 处发生故障时，保护K1 将检测到DG 提供的反向电流。 此时，保护K1 可能误动，切除DG 所在线路使DG 与部分负荷形成孤岛。

1.2 配电网单相接地故障暂态行波特征

本文以图1 的主动配电网系统为例，当线路MN 发生区内单相接地故障后，采用故障分量法分析电路可得故障附加网络中波的折反射模型，如图2 所示。

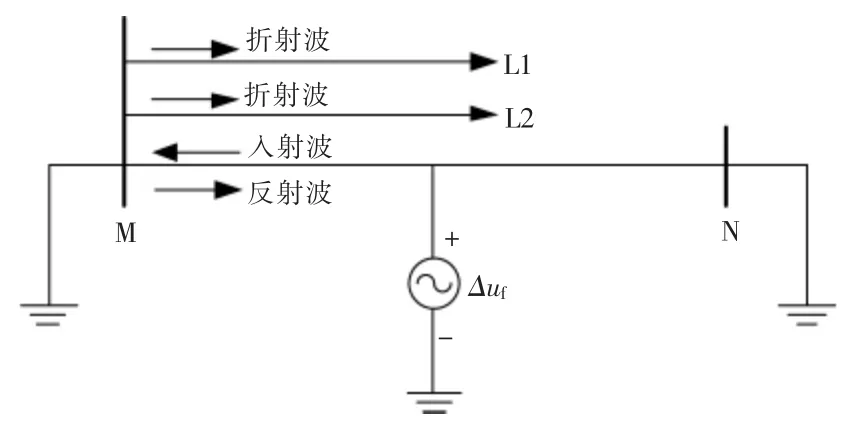
图2 故障附加网络中波的折反射模型Fig.2 A catadioptric model of waves in a fault-attached network

图2 中故障附加电源引起故障行波，行波从故障发生点向母线处传播，并在母线处发生折反射。 行波在母线处的折射得到了非故障线路的初始电流行波，入射波和反射波的叠加得到了故障线路的初始电流行波。

图3 为线路MN 发生区内故障的附加电路。

图3 线路区内故障附加电路Fig.3 Fault additional circuit in the line area

由图3 可知：

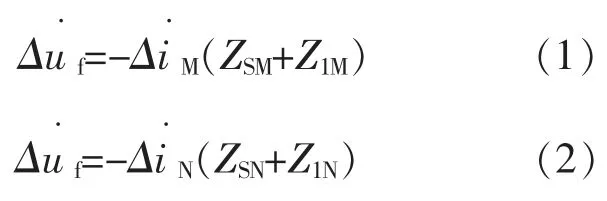
由于ZSM+Z1M，ZSN+Z1N的相角可近似相等，通过式（1），（2）比较可知，对于线路发生区内故障时极性相同。

对于线路M 处保护区外故障附加分量网络如图4 所示。 图中ZMN为线路MN 的阻抗。

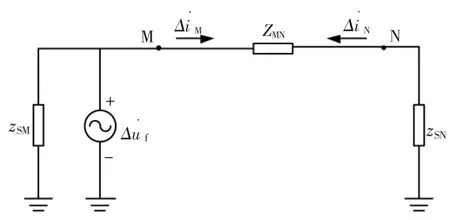
图4 线路区外故障附加电路Fig.4 Line outside fault additional circuit

对于故障后的暂态行波过程，故障点处的故障行波在线路上的传播过程不受DG 接入的影响，其等效模型如图5 所示。

图5 DG 接入母线处等效模型Fig.5 Equivalent model of DG access bus

图中：Z 为线路波阻抗；C 为逆变器输出LC 滤波电路电容；n 为母线出线数。

由图5 可得，DG 经逆变器接入母线处的折反射系数的频域函数为

由式（3），（4）可知，在高频带母线处的折反射系数满足-1<ρ<0，0<γ<1，这表明 DG 的接入不会改变母线处折射波、反射波的极性，即DG 接入对本文所述的利用故障电流初始行波极性的纵联保护方案没有影响。

1.3 电流行波极性比较式纵联保护原理

交流线路MN 中，线路区内故障时，故障点产生的电流行波向两侧传播，线路两端M，N 处测量到的电流行波总是同极性，存在同为正或同为负两种情况。 当故障附加电源电压的极性为上正下负时（正极性），电流行波由故障点向两端传播，与规定的正方向相反，所以M，N 两端电流行波均为负极性。 当故障附加电源电压的极性为下正上负时（负极性），两端电流行波的极性均为正。由此可见，区内故障时线路两端的电流极性相同。 同理，区外故障时，线路两端的电流极性相反。 因此，本文可以通过故障线路两端的电流初始行波极性来判别故障区域，从而实现电流初始行波极性的纵联保护。 电流初始行波极性的纵联保护基本原理如表1 所示。

表1 电流初始行波极性的纵联保护基本原理Table 1 Basic principle of longitudinal protection of current initial traveling wave polarity

设 M 或 N 端电流的行波极性为 Pj，PI为极性判断结果，则：

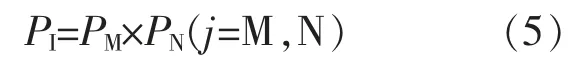
当PI>0 时，判定为区内故障；PI<0 时，判定为区外故障。

2 电流行波极性比较式纵联保护算法

2.1 小波变换及模极大值

在输电线路中，三相故障电流行波之间存在耦合关系，故可采用相模变换技术对三相系统解耦[13]。 本文将电流进行Karenbauer 变换后，可得：

式中：ia，ib，ic分别为 A，B，C 三相电流；iα，iβ，iγ和 i0分别为相电流 Karenbauer 变换的 α 模分量、β 模分量、γ 模分量和0 模分量，其中0 模分量在大地与三相导体之间传播，而α 模分量、β 模分量和γ模分量只在导体之间传播，又称线模分量。α 模分量同时在A 相与B 相导体之间传播，β 模分量同时在A 相与C 相导体之间传播，γ 模分量同时在B 相与C 相导体之间传播。

故障行波最重要的特征是初始波头的奇异性。 小波变换的模极大值可以有效地表征行波信号的突变点，即行波波头[12]。故障行波波头与小波变换后的模极大值具有一一对应的关系，可由模极大值的正负来表示行波波头极性[13]。 故障行波本质上属于非平稳时变信号，若要准确提取其所包含的故障信息，须要在时域和频域同时对信号进行处理。 小波变换具有很好的时频局部化分析性能，适合于对非周期突变信号的分析。本文采用三次中心B 样条函数的导函数作为小波函数，借助三次中心B 样条二进小波变换，利用Mallat 算法分析提取故障初始行波极性[14]，即：

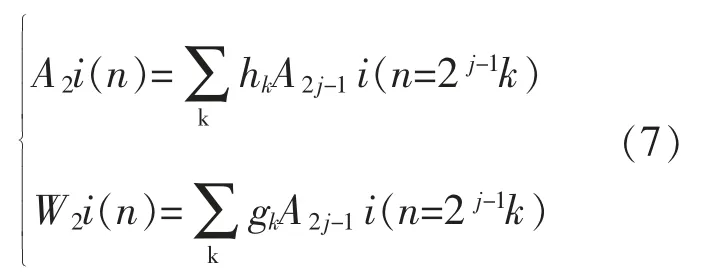
式中：A2i（n）为小波变换结果的逼近分量；W2i（n）为变换结果的小波分量；n为采样序号；j 为小波变换的尺度；hk，gk为由小波函数决定的小波系数；{hk}={0.125，0.375，0.375，0.125} （k=-1，0，1，2）；{gk}={-2，2}（k=0，1） 。

本文用400 kHz 采样率提取故障1 ms 的电流初始行波，用Karenbauer 变换对提取的故障电流初始行波进行相模变换，对得到的线模分量进行二进小波变换，并对变换后的尺度2，3，4 上的小波分量进行分析。 因为电流故障初始行波的波头具有高频特性，故本文取尺度4 上的小波分量构成保护算法，对应的频带为 12.5～25 kHz[15]，[16]。

2.2 保护判据与算法

根据配电网单相接地故障暂态行波特征，得到基于暂态行波的故障保护判据： 母线上共有n回出线，设母线第i 条出线发生单相接地故障，计算在不同尺度下，故障电流行波Ii的小波变换模极大值，对于给定尺度2k的保护判据为

配电网线路发生故障时，故障线路上的继电器检测到故障电流行波，对检测到的故障初始电流行波进行Karenbauer 变换，得到解耦后的3 个模量电流行波 iα，iβ，iγ。 对解耦得到的线模分量电流行波进行二进小波变换，并取变换后尺度4 上的小波分量模极大值极性作为故障初始电流行波模极大值。 如果任意一个模量的初始电流行波模极大值相同，则判断线路发生了区内故障，保护将给出报警或跳闸信号，否则保护闭锁。

综上所述，保护算法流程如图6 所示。

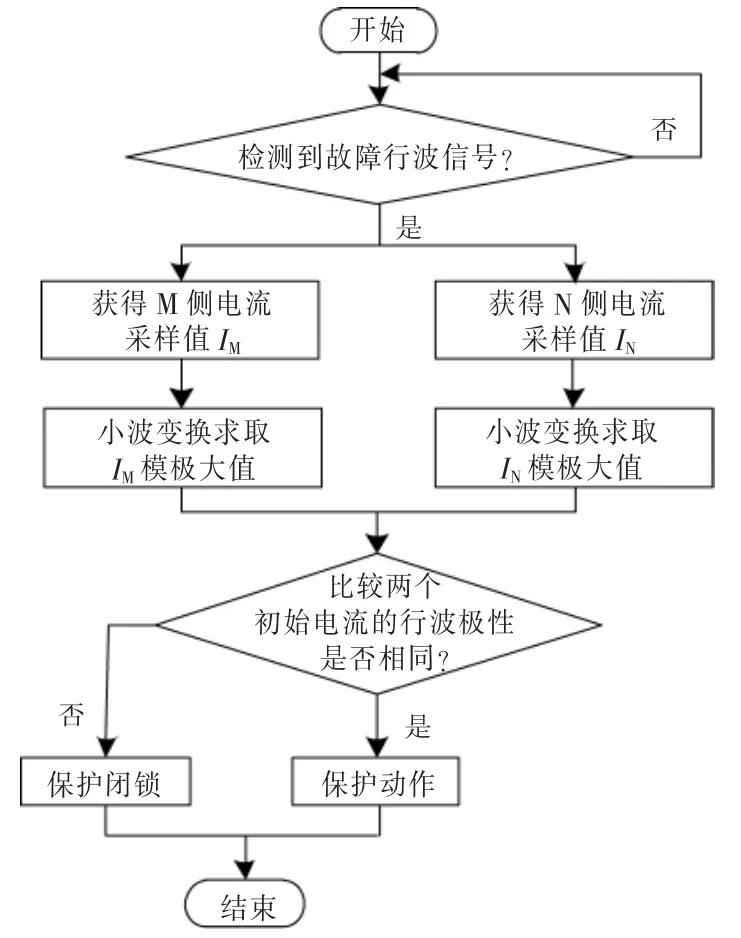
图6 保护算法流程图Fig.6 Protection algorithm flow chart

3 仿真分析

基于PSCAD/EMTDC 电磁暂态仿真软件，以图1 为例搭建仿真模型。 系统基准容量为500 MV·A，基准电压为 10.5 kV，在每条馈线上接有额定容量为 6 MV·A、 额定功率因数为 0.85 的负荷。DG 采用PQ 控制方式，额定容量为10 MV·A，模型线路参数如表2 所示。

表2 线路参数Table 2 Line parameters

3.1 单相接地故障

设系统在 t=0.3 s 时，线路 MN 分别发生区内和区外A 相接地故障，故障持续0.2 s，电流故障行波的数据窗取故障发生后1 ms 的数据。对获取的数据进行处理分析，得到的故障电流初始行波极性仿真结果如图7，8 所示。

由图7 可知，发生A 相接地故障后，故障电流行波的波头和小波变换模极大值点具有一一对应的关系。 根据式（6）可知，线路发生A 相接地故障时电流的γ 线模不存在，图7 的仿真结果也验证了此结论。 母线M 侧和N 侧初始电流行波对应的α 和β 模的模极大值极性相同，由保护判据可以判断线路发生了区内故障，保护将给出报警或跳闸信号。 由图8 可知，M 侧和N 侧电流对应的α 和β 模的电流模极大值极性相反，可判断为是区外故障，保护闭锁。

图7 线路MN 区内A 相接地故障的仿真结果Fig.7 Simulation results of A-phase ground fault in line MN

图8 线路MN 区外A 相接地故障的仿真结果Fig.8 Simulation results of A-phase ground fault outside the line MN

3.2 不同故障类型下保护方案的仿真

对不同故障下的保护动作情况进行了仿真，表3 为线路MN 上发生不同类型故障时的保护动作情况。表中 AB，ABG，ABC 分别为 AB 两相短路故障、AB 两相短路接地故障和三相短路故障。

由表3 可知，系统分别在发生相间短路、两相短路接地及三相短路故障时，该保护方案均可以使故障准确切除。

表3 故障类型对保护的影响Table 3 Effect of fault types on protection

3.3 动作性能分析

3.3.1 系统结构对保护的影响

对不同的中性点接地方式对保护的影响进行了仿真。表4 列出了在不同接地方式下，线路发生故障时保护的动作情况。

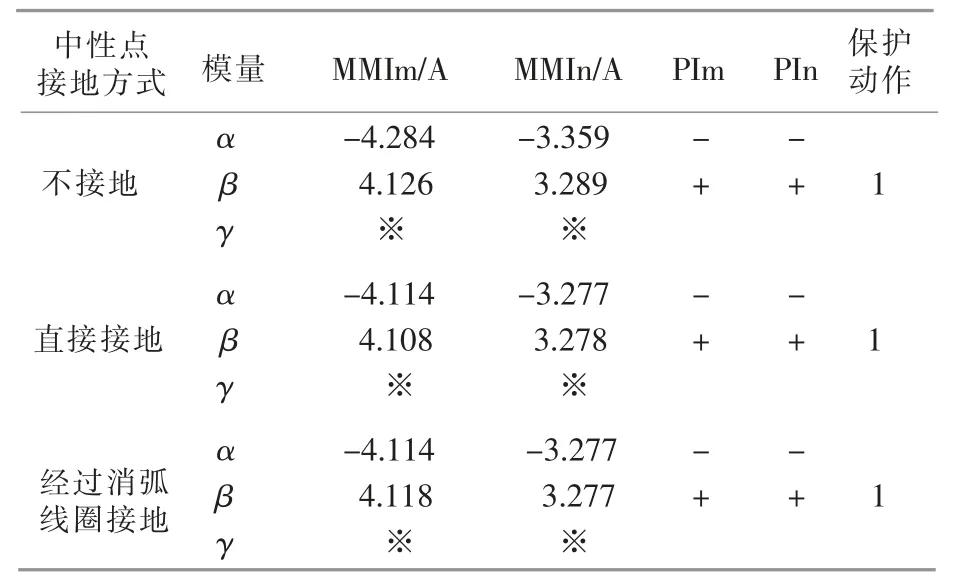
表4 中性点接地方式对保护的影响Table 4 Impact of neutral grounding method on protection

由表4 可知，系统在中性点不接地、 直接接地、经消弧线圈接地的方式下发生故障时，本文保护方案均可以使故障准确切除。

3.3.2 故障距离对保护的影响

为验证行波电流极性比较式纵联保护不受故障距离的影响，分别在距离线路 M 端 1，3，6，10 km 处进行了仿真。

仿真结果如表5 所示。

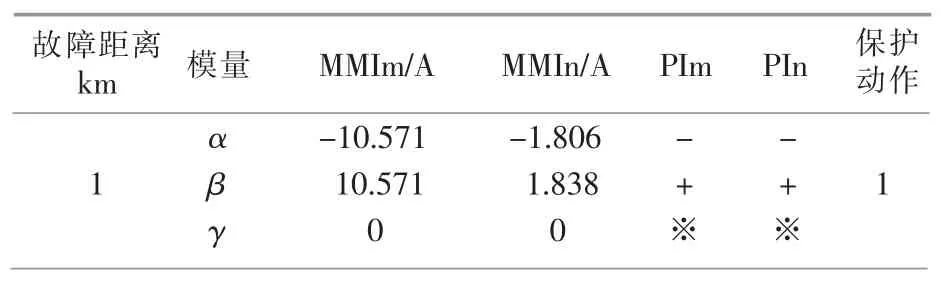
表5 故障距离对保护的影响Table 5 Impact of fault distance on protection

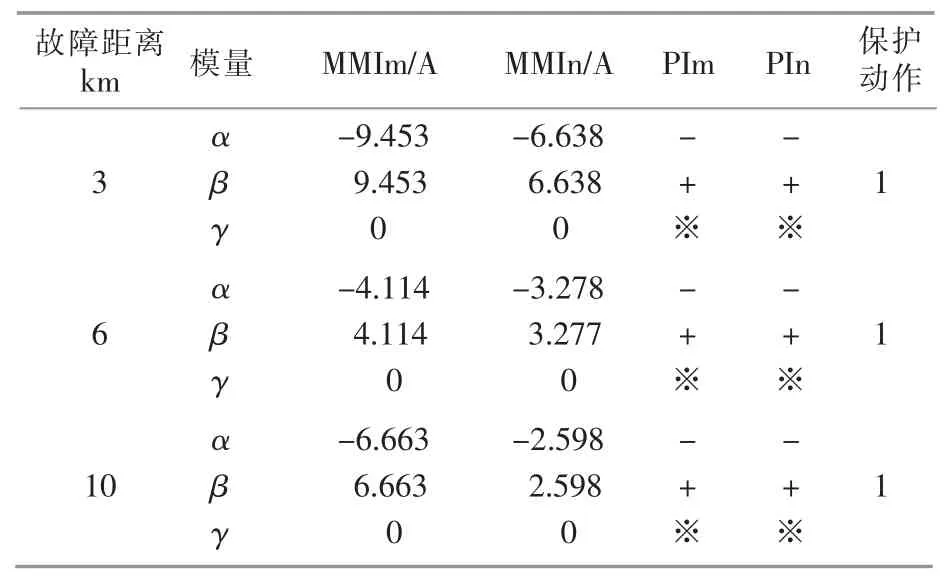
续表5

由表5 可知，在故障距离不同时，该保护方案均可以准确切除故障。

3.3.3 故障过渡电阻对保护的影响

本节考虑线路MN 发生区内A 相接地故障时，取故障过渡电阻分别为 0.1，100，200 Ω，研究故障过渡电阻的改变对保护动作性能的影响。 表6 中给出了在不同过渡电阻时，线路发生故障时保护的动作情况。

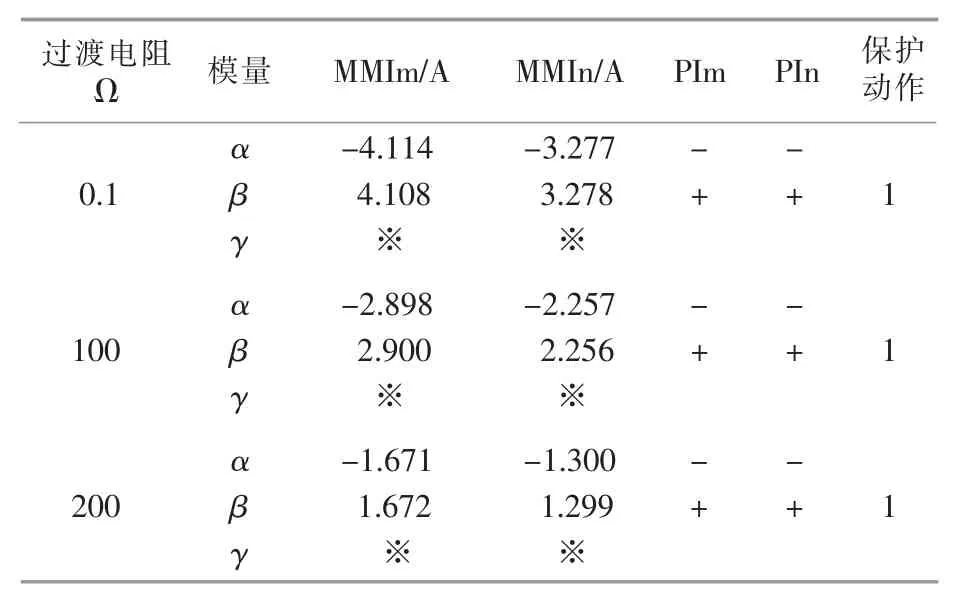
表6 故障过渡电阻对保护的影响Table 6 Effect of transition resistance on protection

由表6 可知，保护受故障过渡电阻的影响较小。 过渡电阻的改变对小波变换的模极大值极性没有影响，只影响小波变换的模极大值的幅值，但故障过渡电阻的增大将会降低保护的灵敏度。

3.3.4 DG 投切对保护的影响

传统单端的配电网供电线路相当于线路接入的DG 容量为0，本文对DG 在不同的投切状态下，保护方案的影响进行了仿真，结果如表7 所示。 线路MN 发生区内A 相接地故障时保护的动作情况。

由表7 可知，DG 的不同状态并未对保护的准确动作造成影响。

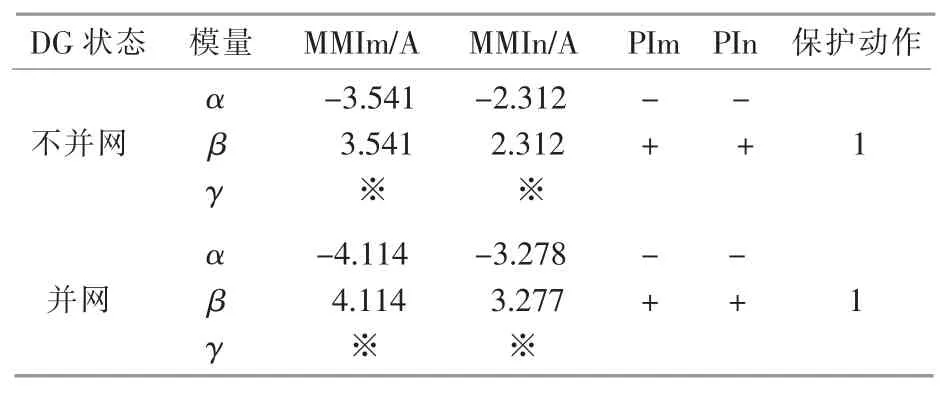
表7 DG 投切对保护的影响Table 7 Effect of DG switching on protection

10 kV 母线处故障行波的折反射过程由母线出线数、线路波阻抗等参数决定，与线路负荷、电源无关。如前文所述，分布式电源易对不具有方向判断的保护线路保护造成误动，而利用电流初始行波极性的纵联保护方法不存在这个问题。

4 结论

本文提出的基于电流初始行波极性的主动配电网纵联保护方案，有效地解决了DG 接入主动配电网后传统电流保护可能发生误动或拒动的问题，使线路故障可靠准确地切除，并得出结论如下。 ①电流初始行波极性的纵联保护采用故障发生后的电流初始行波波头极性作为判据，保护动作速度快且不受对地电容影响，所以不用考虑保护动作延迟的问题。 ②该保护方案可有效判断出线路区外和区内故障，具有良好的方向性，且受中性点接地方式、故障位置、过渡电阻和分布式电源投切的影响相对较小，符合保护安全性可靠性的要求。③该保护判据构成简单，故障电流初始行波有明确的物理意义，其极性不受后续行波折反射过程的影响，特征量明确且容易提取，具有一定的实际工程应用价值。