水平结构竞争-互利群落优化算法*
2020-04-15黄光球陆秋琴
黄光球,陆秋琴
西安建筑科技大学 管理学院,西安 710055
1 引言
工程中经常遇到十分复杂的优化问题,此类优化问题既存在大量局部最优解,其所包含的函数表达式又常常不可导,有时甚至连具体的函数表达式都无法知道。为了求解这些优化问题的全局最优解,目前所采用的方法是启发式方法,群体智能优化算法就是其中的一种,这类优化算法对优化问题的函数表达式没有特殊限制,因而具有较广泛的适用性[1]。常用的群智能优化算法有:遗传算法[2-3]、蚁群算法[4-5]、粒子群算法[6-7]、人工鱼群算法[8]、生物地理学算法[9]、人工免疫算法[10]、蜂群算法[11]等。这类算法是依据一些简单的自然现象而构造出来的,而且这些自然现象难以采用合适的数学模型加以描述。
为了克服传统群智能优化算法存在的缺陷,本文选择一种特殊的自然现象,即水平结构下的生物群落竞争-互利进化现象[12-13],构造出了一种新的群智能优化算法,即水平结构竞争-互利群落优化算法(horizontal structure competition-mutually beneficial community optimization,HS-CBCO)。由于水平结构竞争-互利群落进化系统可采用种群动力学数学模型进行恰当描述,从而使HS-CBCO 算法奠定在坚实的数学理论基础之上。
在自然界,任何种群都有确定的生态区域,它们在该区域中生存和繁衍。事实上,每一种群都占有自己的生态位[12],生态位的镶嵌是现实生物群落中的典型现象[13]。种群不但在同一生境中共存,而且是在消费相同的资源条件下共存。资源的局限性,使利用同一种群的资源相互制约。这样,生态位的镶嵌自然导致竞争关系,生态位决定着种群在竞争的群落结构中的地位和作用,而不存在生态位的镶嵌的种群又会形成互利关系。水平结构竞争-互利群落进化指的是水平结构下生态位存在镶嵌的群落系统中的生物种群相互竞争、互利,共同进化的现象。目前,有关水平结构竞争-互利群落进化系统理论研究已取得如下进展:
(1)群落水平结构特征分析[14-15]。研究群落的水平结构特征,以便对群落规模、营养供给水平和种群竞争和互利特征进行有效控制。
(2)营养水平对群落规模和群落结构的影响[16-17]。研究群落的营养供给水平对群落规模和群落结构的影响,发现其中的种群竞争和互利规律,为合理确定营养供给水平提供科学依据。
(3)群落结构特征对种群变化特征的影响[18]。揭示在种群竞争和互利环境下的群落结构特征对种群变化特征的制约规律,为有效控制种群变化特征提供科学依据。
上述有关水平结构竞争-互利群落进化理论的研究为本文算法的进一步研究提供良好的支撑。本文着重解决如下问题:
(1)如何将水平结构竞争-互利群落动力学模型转化为能求解复杂优化问题的群智能优化算法。
(2)如何使得HS-CBCO 算法中的算子能充分反映不同种群内个体之间的相互作用关系,以便体现水平结构竞争-互利群落动力学理论的基本思想。
(3)如何证明HS-CBCO 算法的全局收敛性。
(4)如何确定HS-CBCO 算法的最佳参数设置。
(5)如何进行HS-CBCO 算法的求精和探索能力及其协调性分析。
2 HS-CBCO 算法设计
考虑优化问题:
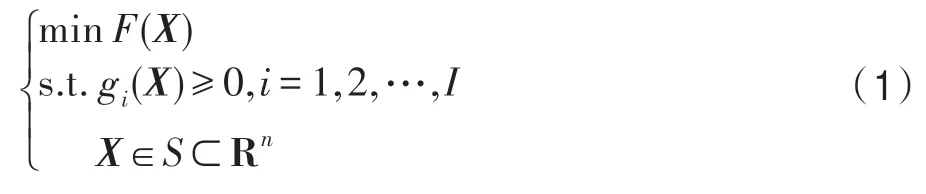
式中,Rn是n维欧氏空间;X=(x1,x2,…,xn)是一个n维决策向量;S为搜索空间;f(X) 为目标函数;gi(X)≥0 为第i个约束条件,i=1,2,…,I,I为不等式约束条件个数。目标函数f(X)和约束条件gi(X)不需要特殊的限制条件。
2.1 算法场景设计
在生态系统中,水平结构是指多个不同类别的生物种群所消费的资源为同一类型。在同一水平结构内的种群间相互作用主要是竞争和互利。假设一个生态系统中有K个种群在其中活动,其编号分别为1,2,…,K,记为P={1,2,…,K}。
时期t,种群k内有Nk(t)个生物个体(简称个体),这些个体的编号的集合记为,因此该生态系统中的个体总数为N(t)=M(K,t),。若按种群编号顺序对所有种群中的个体进行统一编号,则种群k内的Nk(t)个个体的编号为Pk={1+M(k-1,t),2+M(k-1,t),…,Nk(t)+M(k-1,t)}。已知个体的编号为m,当m满足M(u-1,t)<m≤M(u,t)时,该个体所在的种群编号NL(m)=u。
在一个生态系统中,每一种群都占有自己的生态位,生态位是指种群对多种资源的利用范围。当种群的生态位出现镶嵌(又称重叠)时,种群之间会产生竞争关系。生态系统中已发现有5 种竞争格局,即正态分布型(C1)、离散分布型(C2)、最邻近型(C3)、均匀型(C4)、单调递减型(C5),记为C={C1,C2,C3,C4,C5}。
在该生态系统中,不存在生态位镶嵌的种群之间可能存在互利关系,但该互利关系不是一成不变,而是随时间变化的。若一个种群与另外一个种群存在竞争关系,则它们之间就不存在互利关系,反之亦然。
在一个种群的内部,各生物个体之间存在相互影响关系,这种相互影响关系分为两种类型,即普通影响关系和强烈影响关系。所谓普通影响关系是指某个体受到其他普通个体的影响,而强烈影响关系是指某个体受到其他强壮个体的深刻影响。
种群中的生物个体在进化期间,其特征既会受到种群之间的竞争和互利影响,又会受到同一种群内其他生物个体的影响,且这种影响是随时间变化的。
下面将上述现象与优化问题(1)的全局最优解的求解过程对应起来,即有:生态系统与优化问题(1)的搜索空间S相对应,时期t,该生态系统中的一个生物个体对应于一个优化问题(1)的一个试探解,种群k所包含的Nk(t)个生物个体所对应的优化问题(1)的试探解集为,其中,m=1,2,…,Nk(t) ;种群k中的一个个体的特征j对应于优化问题(1)试探解中的一个变量;种群k中所有个体的特征数与试探解的变量数相同,都为n,令个体特征的编号集合Z={1,2,…,n}。个体适应度指数即IPI 指数(individual physique index)对应于优化问题的目标函数值。试探解质量越好,其对应的IPI指数越高,反之亦然。时期t,对于优化问题(1),个体的IPI 指数计算方法为:

2.2 水平结构竞争-互利群落动力学模型
假设种群所消费的资源以某种特性参数向量z表示,具有特征z的资源消耗数量由函数k(z)来确定。函数k(z)中z值的集合称为资源谱。假设一种群资源消费以某种概率分布来描述其特性,其密度函数f(z)称为资源利用函数,具有均值z0和有限方差σ2。这时,种群的生态位取决于资源谱上的点z0和给定的点z0附近随机分布的密度函数f(z)。当一个群落由若干为共同的食物资源而进行竞争的种群构成时,自然认为适合于不同种群的z0点彼此之间有一定距离。这种情况下,种群生态位镶嵌所造成的竞争现象必然会在资源空间里相应的资源利用函数fi(z)产生定义域相交的现象。最简单的例子如图1所示,图中fi(z)为形状相同的正态分布密度曲线,沿着资源谱均值之间以距离d分离;k(z)=const,如果对所有曲线,w为均方差,那么比值w/d可视为生态位接近的度量,或者说是群落种间隔离度度量;按照稳定性条件,比值w/d可以用于判断生态位镶嵌的界限[12-13]。

Fig.1 Niche mosaic of 1-D resource spectrum图1 1 维资源谱的生态位镶嵌
两个种群在资源谱上利用资源的分离程度称为生态位分离。d表示平均分离度,w称为变异度,生态位分离度为d/w。当生态位充分分离时,d/w大;当生态位重叠时,d/w小。
为简单起见,以后总假定资源谱的维数为1 维,即z为1 维,因此可将z的黑体去掉而表示为z。K个种群竞争-互利群落的动力学模型为:
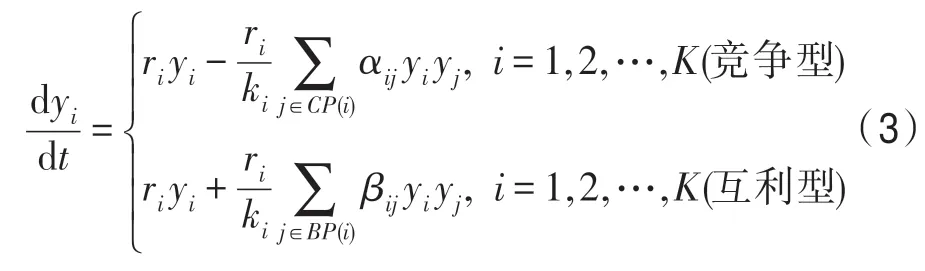
式中,yi为种群i的规模;CP(i)为与种群i竞争的其他种群集合;BP(i)为与种群互利的其他种群集合;ri为种群i的内禀增长率;ki为种群i的生态位容量,ki=∫k(z)fi(z)dz;βij为种群i与种群j之间的互利系数;αij为种群i与种群j之间的竞争系数,由下式计算:

为方便起见,令A=[αij]K×K,A称为竞争矩阵。当A取不同的形式时,表示不同的竞争格局。常见的竞争矩阵A有如下5 种形式:
(1)正态分布型。对于每一个种群i,有:
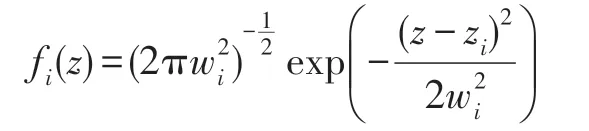
式中,zi为生态位的中心点,为正态分布的方差。如果种群i和种群j生态位的中心点彼此相距dij,那么由式(4)可计算得:

如果所有fi(z)都有相同的方差,且顺序号码相邻就意味着生态位相邻,则dij=|i-j|d,且:
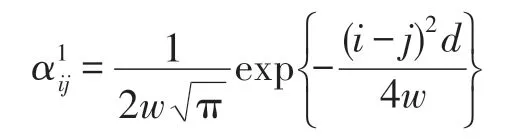
当规定竞争系数的自镶嵌程度为1 时,便有:

(2)离散分布型。将K个种群进行编号,使它们在资源空间彼此距离的大小可用下标差的绝对值|i-j|来度量。不难认为,竞争现象是随种群生态位间距加大而减弱的,于是竞争系数可表示成:

(3)最邻近型。设K个种群中的每一种群仅和自己最邻近的种群竞争,而不和其他种群竞争。这时如果用a表示两个相邻生态位镶嵌的度量,那么竞争矩阵为:
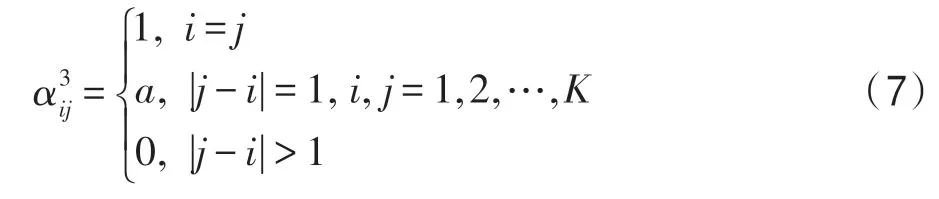
(4)均匀型。设K个种群中的每个种群均以相同的程度a与其他种群竞争,则:

(5)单调递减型。设K个种群中的每个种群均以单调递减的程度a与其他种群竞争,则:

为快速计算,需将式(3)改为离散递推形式:
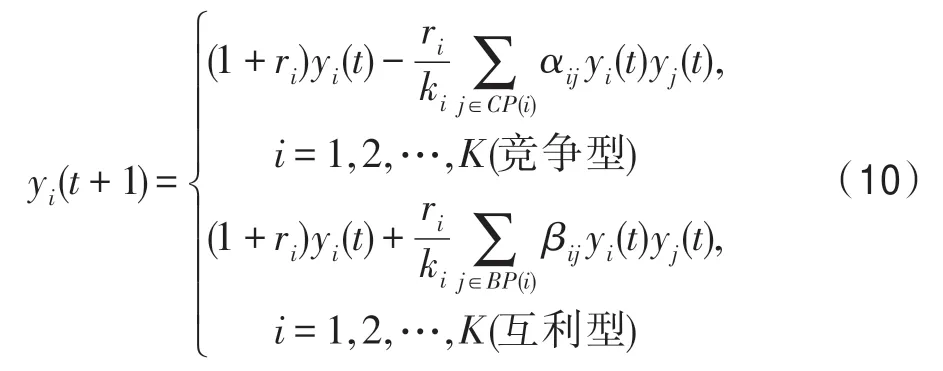
2.3 算子设计方法
HS-CBCO 算法是利用水平结构竞争-互利群落动力学理论构造种群演化算子,以实现生物个体间信息交换,进而实现对优化问题(1)的全局最优解的搜索。
2.3.1 竞争和互利种群集合确定方法
对于当前种群k,k∈P,其竞争型种群集合CP(k)是依据竞争格局类型c确定的,即对于c∈C,有:
(1)若c=C1或C2或C5,则从种群集合P中选择3 个编号最相近的种群,由其编号形成集合CP(k),但k∉CP(k);种群i与种群k编号相近意味着|k-i|尽可能小,但k≠i。
(2)若c=C3,则将K个种群按其编号构成一个闭环,即当k=1时,CP(k)={2,K};当1 <k<K时,CP(k)={k-1,k+1};当k=K时,CP(k)={1,K-1}。
(3)若c=C4,则从K个种群中随机选择3 个种群,由其编号形成集合CP(k),但k∉CP(k)。
对于当前种群k,k∈P,其互利型种群集合BP(k)是从不参与竞争的种群集合P-CP(k)中随机选择3 个种群,这些种群与当前种群k形成互利关系集合BP(k),但k∉BP(k)。
2.3.2 特征生物个体集合确定方法
对于当前种群k,k∈P,当前个体i∈Pk,有:
(1)竞争型个体集合CI(k)。从当前种群k的竞争型种群集合CP(k)中的所有生物个体中,随机选择L个生物个体,由其编号形成竞争型个体集合CI(k)。L称为施加影响的个体数。
(2)互利型个体集合BI(k)。从当前种群k的互利型种群集合BP(k)中随机选择L个生物个体,由其编号形成互利型个体集合BI(k)。
(3)普通影响型个体集合GI(k)。在当前种群k的所有个体集合Pk中,随机选择L个生物个体,由其编号形成普通影响型个体集合GI(k)。
(4)强烈影响型个体集合SI(k)。在当前种群k的所有个体集合Pk中,随机选择L个生物个体,这些个体的IPI 指数高于当前个体i,由其编号形成强烈影响型个体集合SI(k)。
(5)虚弱个体集合WI(k)。在当前种群k的所有个体集合Pk中,随机选择L个IPI 指数最低的生物个体,由其编号形成虚弱个体集合WI(k)。
2.3.3 算子设计方法
HS-CBCO 算法利用水平结构竞争-互利群落动力学理论及其控制下的种群演变规律构造种群演化算子,来实现个体间的信息交换,进而实现对优化问题全局最优解的搜索。HS-CBCO 算法的群演化算子如下所述。
(1)竞争算子。该算子依据竞争关系构造,对当前种群k来说,k∈P,当前个体i∈Pk,由式(10)得:
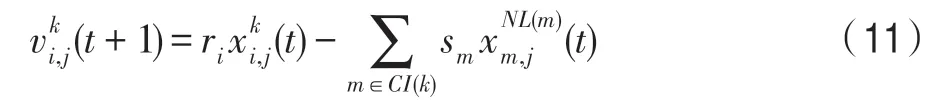
(2)互利算子。该算子依据互利关系构造,即对当前种群k来说,k∈P,当前个体i∈Pk,特征j∈Z,则由式(10)可得:
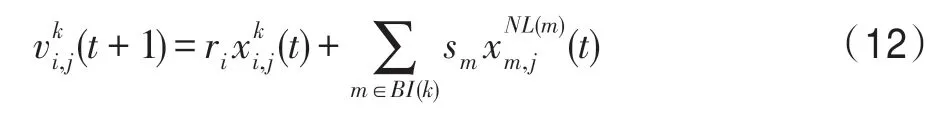
(3)普通影响算子。该算子依据普通影响关系构造,即对于当前种群k,k∈P,当前个体i∈Pk,特征j∈Z,有:
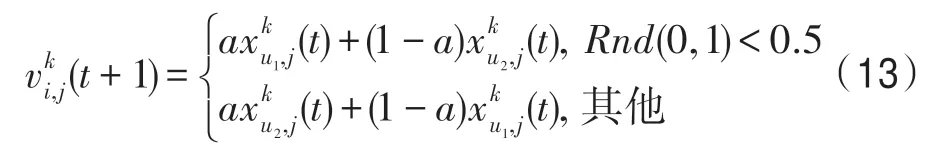
式中,u1、u2从GI(k)中随机选择,且满足u1≠u2;a=Rnd(-0.5,0.5)。
(4)强烈影响算子。该算子依据强烈影响关系构造,即对于当前种群k,k∈P,当前个体i∈Pk,特征j∈Z,有:

式中,v1、v2从SI(kU)中随机选择,且满足v1≠v2;γ=Rnd(-1,1)。
(5)新生算子。该算子用于为某个种群新生m个新个体,即对于种群k,k∈P,待新生的个体编号集合为NGk(m),有:
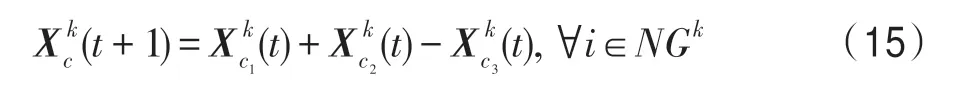
式中,新生个体的编号c∈NGk(m);c1、c2、c3从集合SI(k)中随机选择。
(6)死亡算子。该算子用于为某个种群清除m个虚弱个体,即对于种群k,k∈P,从集合WI(k)中挑出m个体进行清除。
(7)选择算子。通过各算子产生新一代生物个体之后,将新一代个体与相应的父代个体进行比较,较优者保存到下一代中。对于当前种群k,k∈P,当前个体i∈Pk,有:
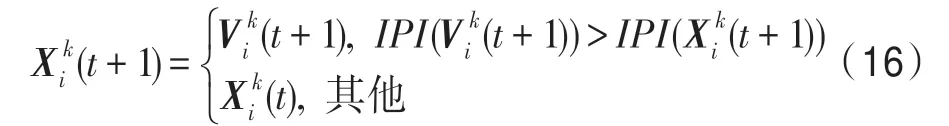
2.4 HS-CBCO 算法设计
(1)初始化:令时期t=0,按第4.1 节介绍的方法设置HS-CBCO 算法涉及到的所有参数:演化时期数G、全局最优解计算误差ε、个体特征受影响的最大概率E0、施加影响的个体数L、种群数K;随机选择当前初始最优解X*。
(2)按第4.1 节介绍的方法设置水平结构竞争-互利群落动力学模型参数yi(0),令Ni(0)=[yi(0)],i=1,2,…,K;[y]表示对y取整;对各种群中的所有个体进行统一编号,生成个体集合,k=1,2,…,K。
(4)在竞争-互利格局集合C中为生态系统随机指定一种竞争-互利格局c,依据c计算竞争矩阵A。
(5)执行下列操作:


(6)结束。
2.5 HS-CBCO 算法的特点
(1)Markov 特性。从HS-CBCO 算法各算子的定义式(11)~式(15)知,时期t+1任何一新试探解的生成只与该试探解在时期t的状态有关,而与该试探解在时期t以前是如何演变到时期t的状态的历程无关,因而HS-CBCO 算法具有Markov 特性。
(2)“步步不差”特性。从生长算子的定义式(16)知,HS-CBCO 算法的每步演化都不会向比当前状态更差的状态转移,因而HS-CBCO 算法的演化过程具有“步步不差”特性。
2.6 HS-CBCO 算法的时间复杂度
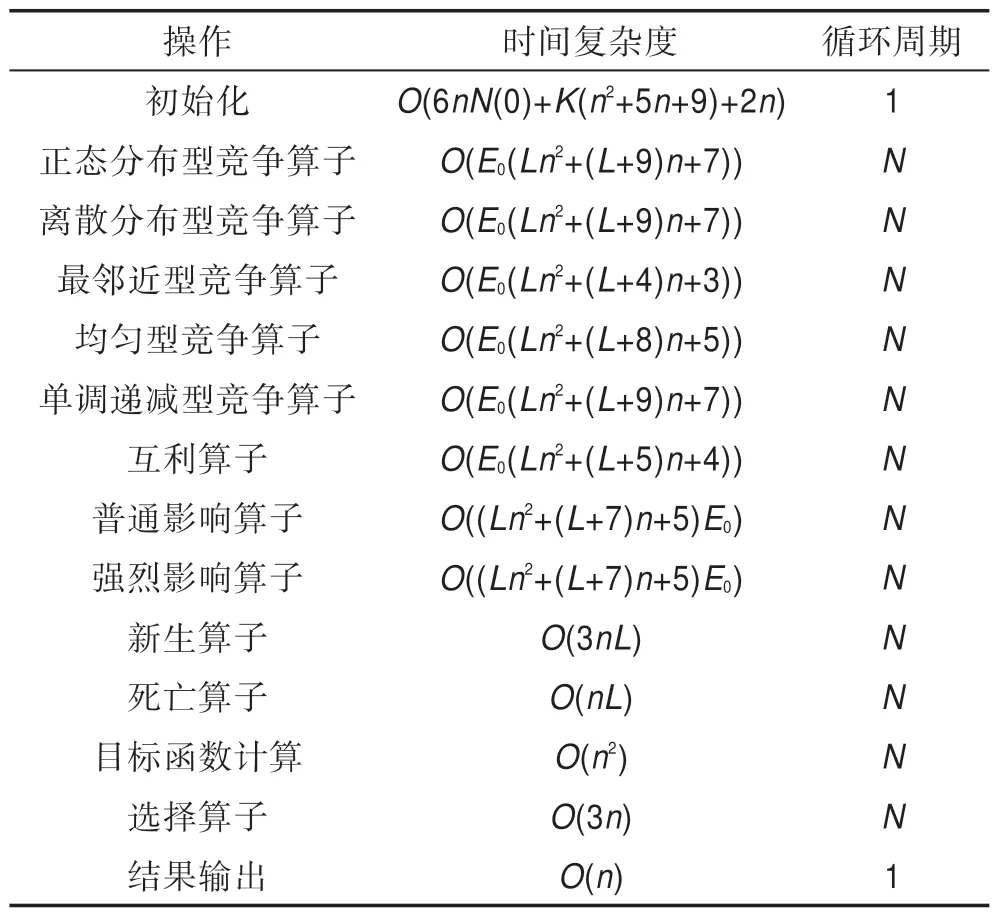
Table 1 Table of HS-CBCO time complexity表1 HS-CBCO 时间复杂度计算表
2.7 HS-CBCO 算法的优势
定理1 若一个群智能优化算法所拥有的算子越多,且各算子被随机独立调度执行,则该算法的性能越优良。
证明 假设一个群智能优化算法有n个算子,当该算法求解优化问题X时,这n个算子求解优化问题X成功的概率分别为p1,p2,…,pn。因每个算子在求解优化问题X时均是被随机独立调度执行的,故该算法在其n个算子的联合作用下求解优化问题X成功的概率q为:
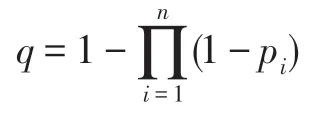
因0 <pi<1,故0 <1-pi<1,i=1~n;当n越大时,越小,而q则越大。此结论表明,若一个群智能优化算法的算子越多,则该算法求解一个优化问题时成功的概率越大。因此,算子越多,算法性能越优良。
HS-CBCO 算法拥有10 个算子,且每个算子均是被随机调度执行的,故HS-CBCO 算法满足定理1 的条件,因而HS-CBCO 算法具有优良的性能。 □
与已有的基于种群动力学的优化方法[19-20]相比,HS-CBCO 算法具有如下异同点:
(1)HS-CBCO 算法所依据的生物场景中详细考虑了生物种群的水平营养结构特点,而现有的其他基于种群动力学的优化方法没有考虑这一关键特征。
(2)HS-CBCO 算法将种群动力学中一些常规特征,如竞争、互利等特征,也包含到了算法中,该特点与基于种群动力学的优化方法类似。
(3)由于存在上述(1)和(2)的特点,HS-CBCO 算法比基于种群动力学的优化方法拥有更多的算子,故该算法特别适合应用于分布式多任务环境,如云计算环境。
3 HS-CBCO 算法的全局收敛性证明
在证明HS-CBCO 算法的全局收敛性之前,先介绍由Iisufescu 在文献[21]提出的定理:
定理2 设P′是一N阶可归约随机矩阵,也就是通过相同的行变换和列变换后可以得到P′=,其中C是M阶本原随机矩阵并且R≠0,T≠0,则有:

上述的矩阵是一个稳定的随机矩阵且P′∞=1′P′∞,P′∞=P′0P′∞唯一确定并且与初始分布无关,P′∞满足如下条件:

利用定理2,不难证明HS-CBCO 算法的全局收敛性。其证明过程如下所述。
由算法HS-CBCO 算法知,优化问题(1)的搜索空间等价于一个生态系统,该生态系统有K个种群;在时期t,种群k有Nk(t)个生物个体,k=1,2,…,K;将各种群中的所有生物个体重新排列成N(t)个生物个体,,形成新的生物个体序列为。每个生物个体(i=1,2,…,N(t))即为优化问题(1)的一个试探解,其目标函数值为(按式(1)计算),则所有生物个体的状态所形成的集合为:
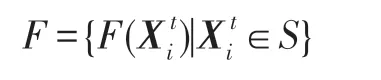
进一步令:
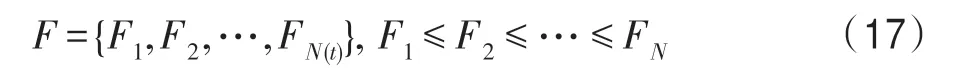
不失一般性,令F1即为所求的全局最优解。将式(17)的下标取出形成一个集合,即:

集合U中的元素就是随机搜索时每个生物个体可能所处的状态。假设在某时期搜索到的最好目标函数值为Fi,其对应的状态为i。显然,由式(17)知,下一时期搜索时,若向更优的状态k转移,则应满足k<i;相反,若向更差的状态k转移,则应满足k>i,如图2 所示。
∀Xt∈S有F1≤F(Xt)≤FN,将S划分为非空子集为:
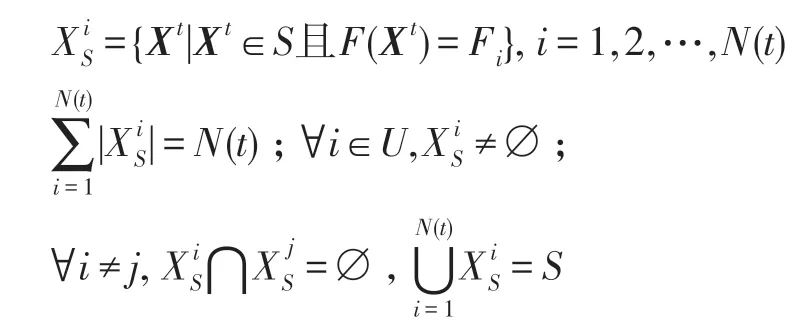

Fig.2 State transition in random search图2 随机搜索时状态转移图



证明(1)对于式(19),设状态i为时期t某生物个体Xt的状态,该状态i当然就是该生物个体至今已达到的最好状态。在HS-CBCO 优化算法中,每次进行新的演化都总是对该生物个体当前状态i进一步向更好状态的更新,即有:
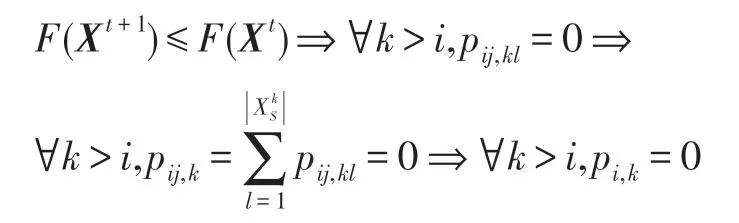
上式的含义是:若i为时期t某生物个体的状态(也必是该个体已达到的最好状态),在时期t+1 该生物个体的演化只会向更好的状态更新,因此从i开始不可能转移到比i差的任何其他状态上去;由式(17)知,若要Fk>Fi,则比状态i差的状态k必满足k>i,也即最好状态要么保持原状,要么只能向更好的状态更新(即做到步步不差),如图2 所示。
(2)对于式(20),设某生物个体的当前状态为i,当然必是该生物个体迄今为止已达到的最好状态,在时期t+1,该生物个体随机选择各种算子以期转移到更好的状态上,有竞争算子、互利算子、普通影响算子、强烈影响算子可供选择:
①若i是全局最优状态,即i=1,则下一步转移必选k=1(因为不可能转移到比当前状态还差的状态上去),即必以概率p1,1=1 转移到该全局最优状态上去。因p1,1=1 >0,命题得证。
②若i不是全局最优状态,则在全局最优状态1和当前状态i之间必至少存在一中间状态k(如图2所示),使得F1≤Fk<Fi,即1 ≤k<i,此时当前状态i可以转移到状态k上去(因为新状态k比当前状态i更优),也就是pi,k>0,命题得证。
综合上述情况,可得∃k<i,pi,k>0。 □
定理3 HS-CBCO 算法具有全局收敛性。

根据引理中式(20)结论得:
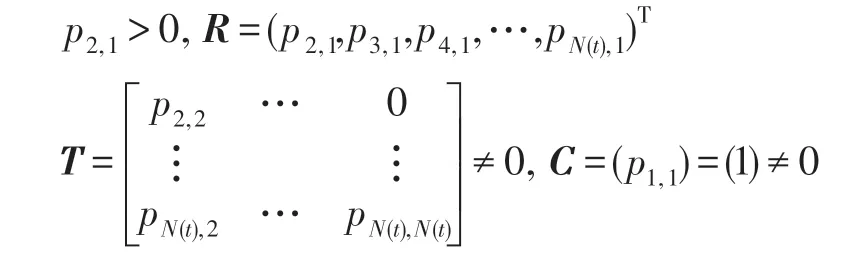
由以上可知转移矩阵P′是N(t)阶可归约随机矩阵,满足定理2 的条件,因此下式成立:

因C∞=C=(1),T∞=0,故必有R∞=(1,1,…,1)T,这是因为由式(18)知转移矩阵P′中每行的概率之和为1。因此有:

上式表明,当k→∞时,概率pi,1=1,i=1,2,…,N(t),也即无论初始状态如何,最后都能以概率1 收敛到全局最优状态1 上。于是得:
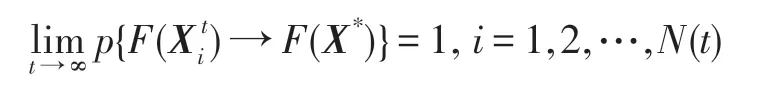
因此,HS-CBCO 优化算法具有全局收敛性。□
4 HS-CBCO 算法参数设置及其普适性
4.1 参数设置方法
HS-CBCO 算法参数包括两部分:一部分是水平结构竞争-互利群落动力学模型参数,该部分参数为算法内置参数,无需用户进行设置;另一部分是算法运行控制参数,此类参数需要用户根据情况进行设置。
(1)水平结构竞争-互利群落动力学模型参数确定方法。该模型参数的选择依据是确保yi(t)(i=1,2,…,K)具有较好的随机性。依据文献[12]介绍的参数取值方法并经随机化后,可得ri=Rnd(0.3,0.4),ki=Rnd(20,30),yi(0)=Rnd(60,70),i=1~K;a=0.5,βij=Rnd(0.17,0.24),i,j=1~K。应用此取值策略,当K=10 时,任取第5 号种群进行测试,种群中的个体数y5变化情况如图3 所示。从图3 可知,y5具有很好的随机性。
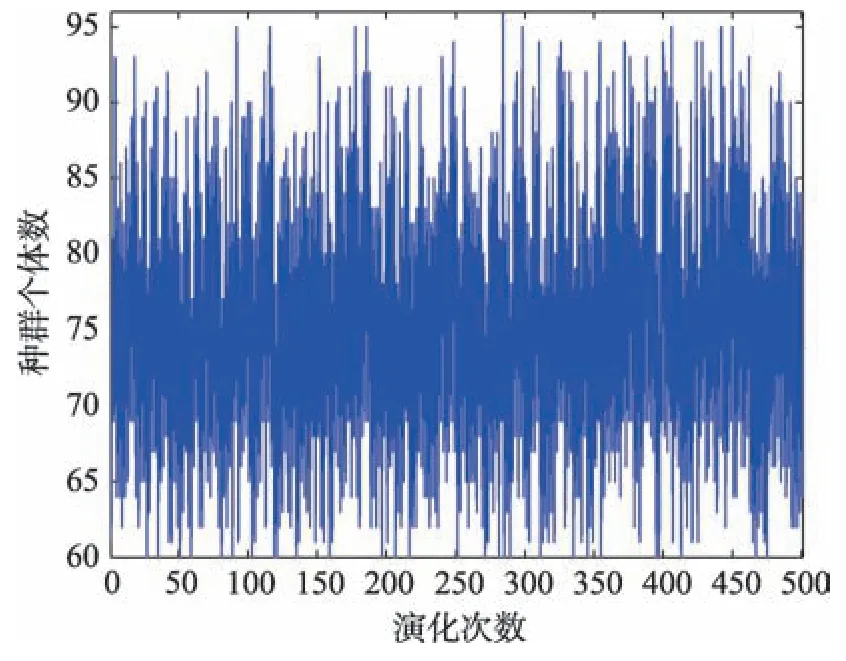
Fig.3 Randomicity of individual y5in population 5图3 第5 号种群中个体y5的随机性
(2)算法运行控制参数设置方法。HS-CBCO 算法的运行控制参数有:演化时期数G、全局最优解计算误差ε、个体特征受影响的最大概率E0、施加影响的个体数L、种群数K。G和ε是两个互补参数,只要满足其中一个即可。ε由所求解的工程优化问题决定,通常可取ε=10-5~10-10即可,G由计算设备性能决定,G可取充分大,不妨设G=108~1010。HS-CBCO算法关键参数只有E0、L、K。因此,下面主要讨论3 个关键参数E0、L、K的取值方法。由于Bump 优化问题极难求解,且与一些工程优化问题特征类似,故以Bump 优化问题为例来探明E0、L、K的取值方法。Bump 优化问题如下:
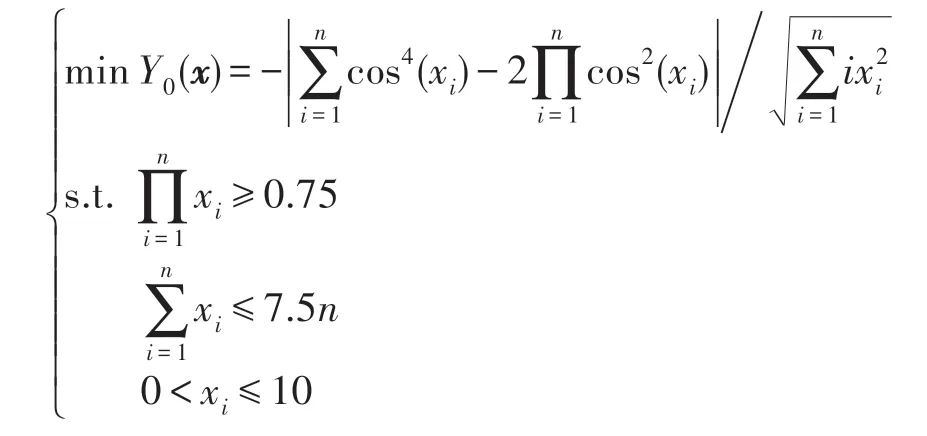
令Favg表示平均最优目标函数值,Tavg表示平均计算时间。当L取不同值时,采用HS-CBCO 算法求解Bump 优化问题,令n=50,E0=0.01,K=10,G=108,运行50 次,表2 描述了L与Favg和Tavg之间的关系。结果表明,当L=3~6 时,Favg的精度达到最高,而Tavg增加较低。由此可见,L=3~6 为L的最佳取值区间。
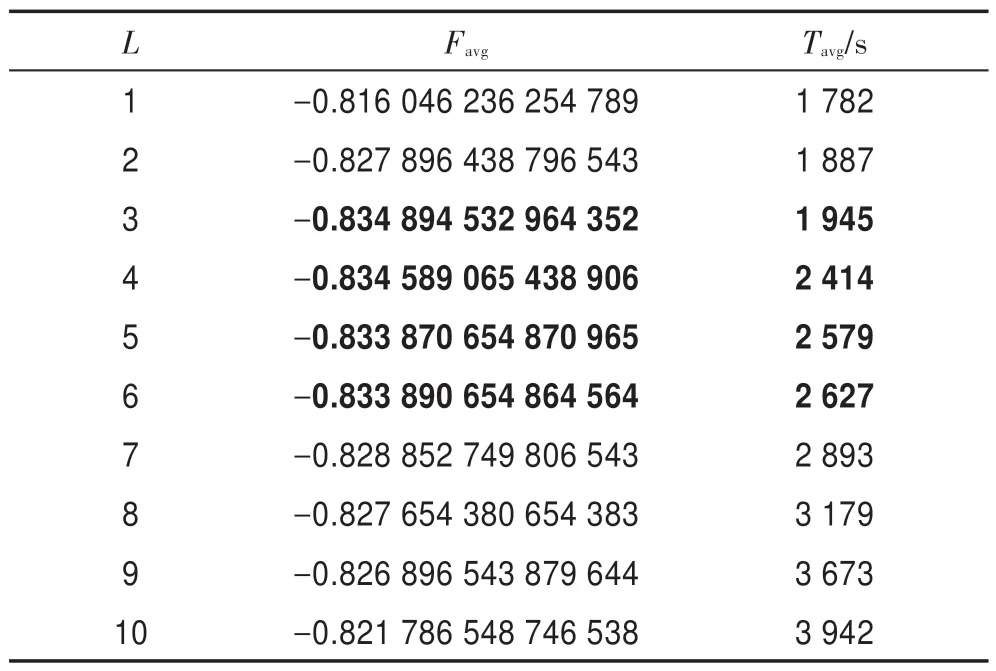
Table 2 Relation of L with Favgand Tavg表2 L 与Favg和Tavg之间的关系
令n=50,L=3,K=10,G=108,HS-CBCO 算法运行50 次。表3 描述了参数E0与Favg和Tavg之间的关系。结果表明,当E0=0.006~0.1 时,Favg的精度相对较高,且Tavg较少;当E0>0.2 时,Tavg增加很大,且Favg精度也大大降低;特别是当E0=1 时,无法获得最佳解。由此可见,E0=0.006~0.1 为E0的最佳取值区间。
令E0=0.01,L=3,G=108,HS-CBCO 算法运行50 次。表4 描述了K与Favg、Tavg之间的关系。从表4 可以看到:当K=8~16 时,Favg的精度相对较高,且Tavg较少;当K>18 时,Tavg增加很大,且Favg精度也逐步降低。由此可见,K=8~16 为K的最佳取值区间。
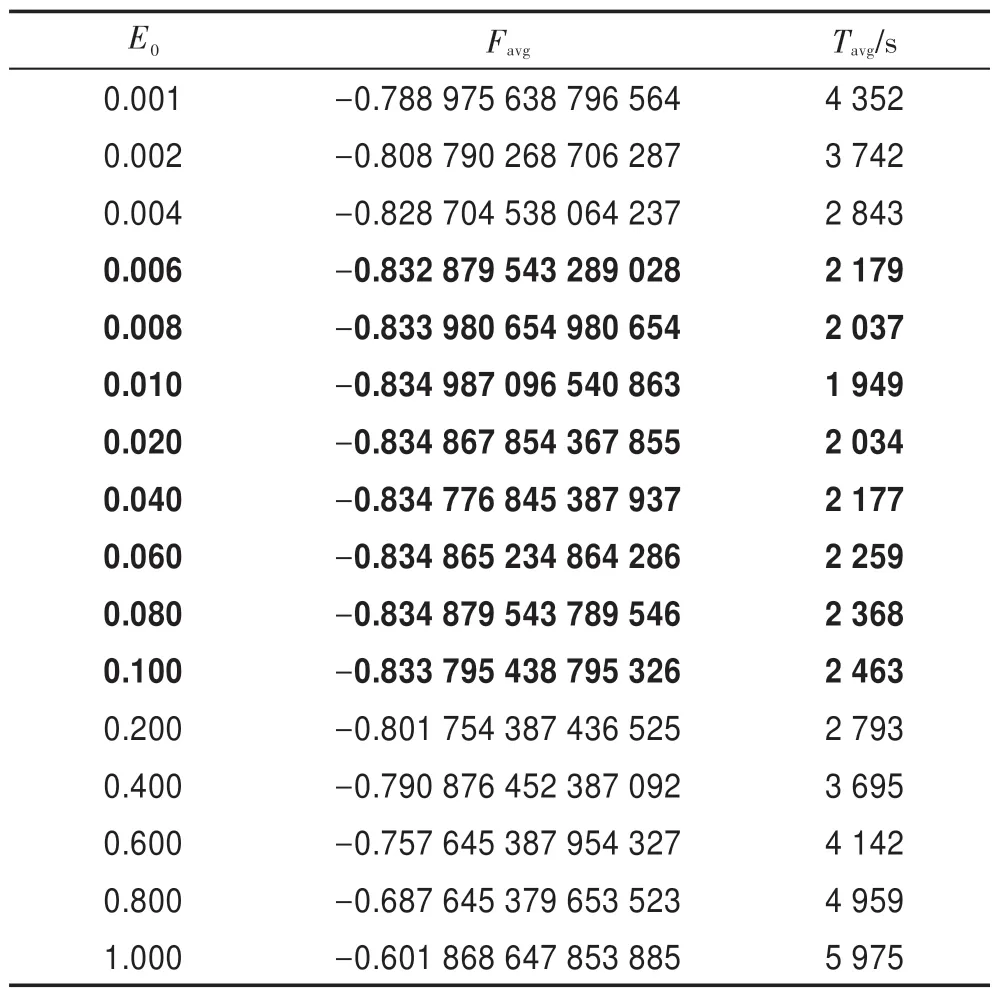
Table 3 Relation of E0with Favgand Tavg表3 参数E0与Favg和Tavg之间的关系
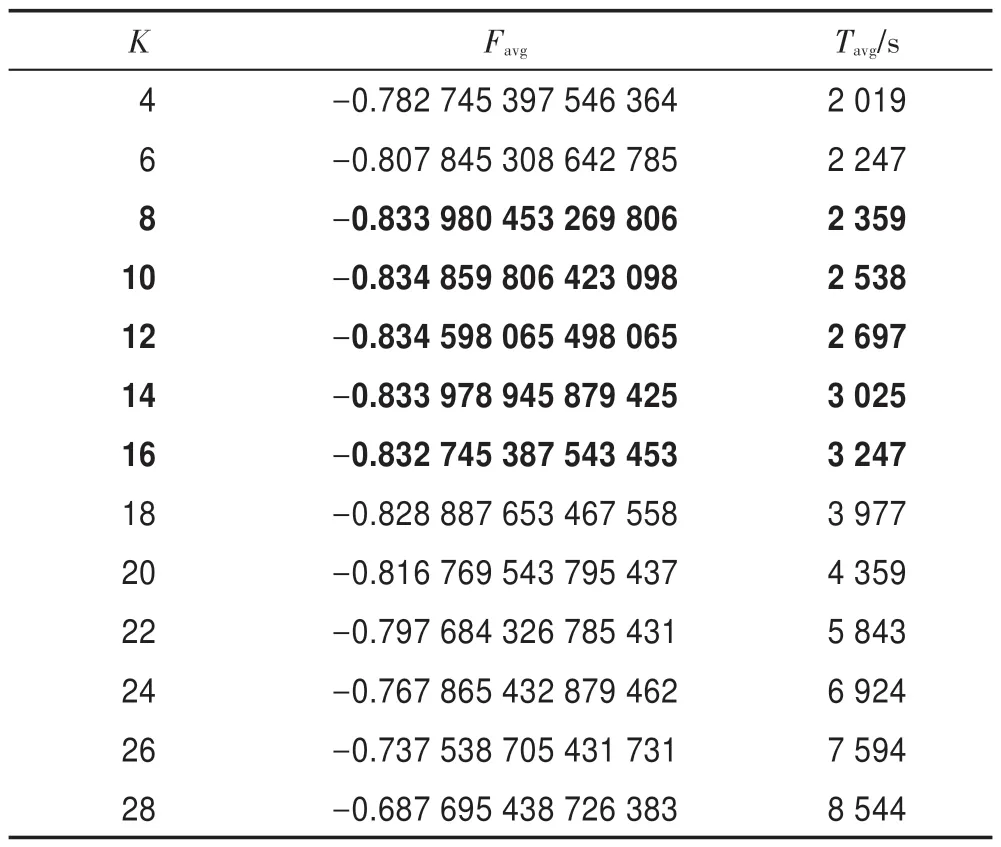
Table 4 Relation of K with Favgand Tavg表4 K 与Favg和Tavg之间的关系
4.2 参数设置的普适性分析
4.1 节确定了参数L、E0、K的最佳取值区间。由于Bump 优化问题与工程中存在的一类优化问题相似,因此从求解Bump 优化问题所获得的参数设置,具有一定的普适性。事实上,参数L、E0、K的取值并不要求太精确,不精确的参数取值仅影响计算时间的长短,对求解精度的影响较小。优化问题的维数n对HS-CBCO 算法的求解时间有影响,参数L、E0、K的取值规律是,优化问题的维数n越高,L和K的取值应越大,E0的取值应越小。根据场景及需求进行参数调整的思路如下:
(1)若n≤100,则L=3,E0=0.01,K=8~10。
(2)若100 <n≤500,则L=4,E0=0.005,K=9~12。
(3)若500 <n≤1 000,则L=5,E0=0.000 1,K=11~14。
(4)若n>1 000,则L=6,E0=0.000 05,K=13~16。
5 HS-CBCO 算法与其他算法的性能比较
CEC 2013[22]是一组新的群智能优化算法测试函数,该组测试函数包含有28 个经过精心设计的基准函数,这些基准函数是由一些传统的著名测试函数(如Sphere 函数、Schwefel 函数、Rastrigrin 函数、Ackley 函数、Griewangk 函数、Rosenbrock 函数等)经改造而得,改造方法包括复杂旋转和平移、条件数大幅提高和多函数镶嵌等,从而使得这些基准函数不再关于某点对称,其表达式高度复杂,理论全局最优解可随机设置。这28 个基准函数共分3 类:第一类是由F1~F5 等5 个单峰函数组成,这些单峰函数包含有极高的条件数,主要用于测试算法的求精能力;第二类是由F6~F20 等15 个多峰函数组成,这些多峰函数是由上述著名的测试函数经旋转平移后而形成,主要用于测试算法的探索能力;第三类是由F21~F28等8 个复合函数组成,这些复合函数是由若干个第一类和第二类函数经复杂镶嵌而形成,其函数表达式异常复杂,主要用于同时测试算法的求精能力和探索能力的协调性。本文选择了6 个代表性的基准函数,每类选2 个,如表5 所示。
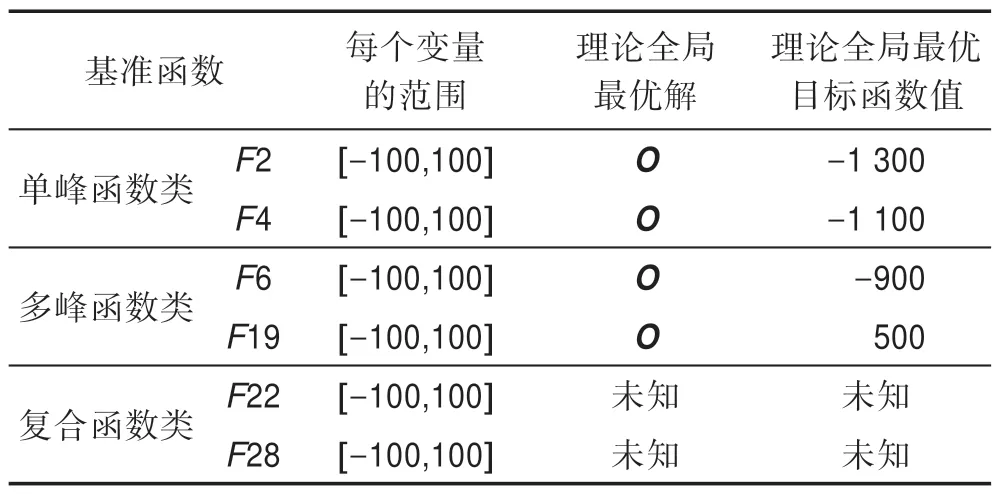
Table 5 Benchmark function optimization problems表5 基准函数优化问题
在表5 中,优化问题的维数为n;O是一个n维决策向量,O的值随机产生。这些基准函数的形式可参见文献[22]。
用HS-CBCO 算法去求解表5 所示的6 个基准函数,HS-CBCO 的参数设置为n=50,ε=10-10,K=10,L=3,E0=0.01,G=1010。与HS-CBCO 算法进行比较的优化算法为:RC-GA(real-coded genetic algorithm)[2]、DASA(differential ant-stigmergy algorithm)[4]、NP-PSO(non-parametric particle swarm optimization)[23]、MBBO(metropolis biogeography-based optimization)[9]、DE(differential evolution)[24]、SaDE(differential evolution algorithm with self-adaptive strategy)[25]和ABC(artificial bee colony algorithm)[11]。计算时,这7 种算法的参数按表6 进行设置。RC-GA 是一种新型实数编码遗传算法,其中的算子采用实数编码设计,完全不同于传统的GA 算法;DASA 是一种模仿蚁群算法的思路而完全重构的新型算法;NP-PSO 是一种不需要进行参数设置的粒子群算法;MBBO 对传统的生物地理学算法的岛屿特征进行了大幅修改,强化了都市特征;DE 是在传统差分进化算法中引入了局部诱导遗传算子的新型差分进化算法;SaDE 在传统自适应差分算法中引入了一种新的自适应参数控制策略;ABC 是在传统蜂群算法中引入了基因组合的蜂群算法。这7 个算法是其对应传统算法的较优改进版,特别适合求解高条件数单峰、多峰复合优化问题。
用这些算法独立求解每个基准函数51 次,表7列出了最优目标函数的平均值(Average)、中位数(Median)、标准差(STD)、计算时间(Time),并对每种算法进行排序。表7 的Rank1 是按该算法的平均最佳目标函数值的精度进行的排名,Rank2 是按平均最佳目标函数的精度与平均计算时间的长短两者综合进行的排名。

Table 6 Parameter settings of compared algorithms表6 被比较算法的参数设置
从表7 可以看出各算法的排名按精度或按精度+计算时间的最终排名均为:
HS-CBCO>SaDE>DE>DASA>MBBO>ABC>NP-PSO>RC-GA
图4(a)~图4(f)说明各算法求解6 个基准函数时的样本收敛曲线。为了突出这些样本收敛曲线的变化,水平和垂直轴采用对数刻度。
6 HS-CBCO 算法的性能分析
6.1 求精和探索能力及其协调性分析
(1)求精能力分析。从图4(a)~图4(f)可知,HSCBCO 算法的收敛曲线在一些时间段内较其他算法的收敛曲线上升缓慢,且持续时间长。此说明HSCBCO 算法提升最优解精度的演化十分明确,该特征表明HS-CBCO 算法的求精能力较其他算法强。另外,由表7 可知,HS-CBCO 算法求解F2、F4、F6、F19时,能获得其理论全局最优解;HS-CBCO 算法求解F22、F28 时,所获得的全局最优解均优于其他被比较算法。此说明HS-CBCO 算法较其他被比较算法具有更好的求精能力。
(2)探索能力分析。从图4(a)~图4(f)可知,HSCBCO 算法的收敛曲线在一些时间段内较其他算法的收敛曲线陡,此说明HS-CBCO 算法提升IPI 指数的耗时很短,该特征表明HS-CBCO 算法探索新空间的能力较其他被比较算法更强。
(3)求精和探索能力的协调性分析。从图4(a)~图4(f)可知,与其他被比较算法相比,HS-CBCO 算法的缓(求精能力)和陡(探索能力)交替出现,且缓的持续时间均较长,陡的持续时间均较短,此表明HS-CBCO 算法的求精和探索能力的协调性均优于其他被比较算法。
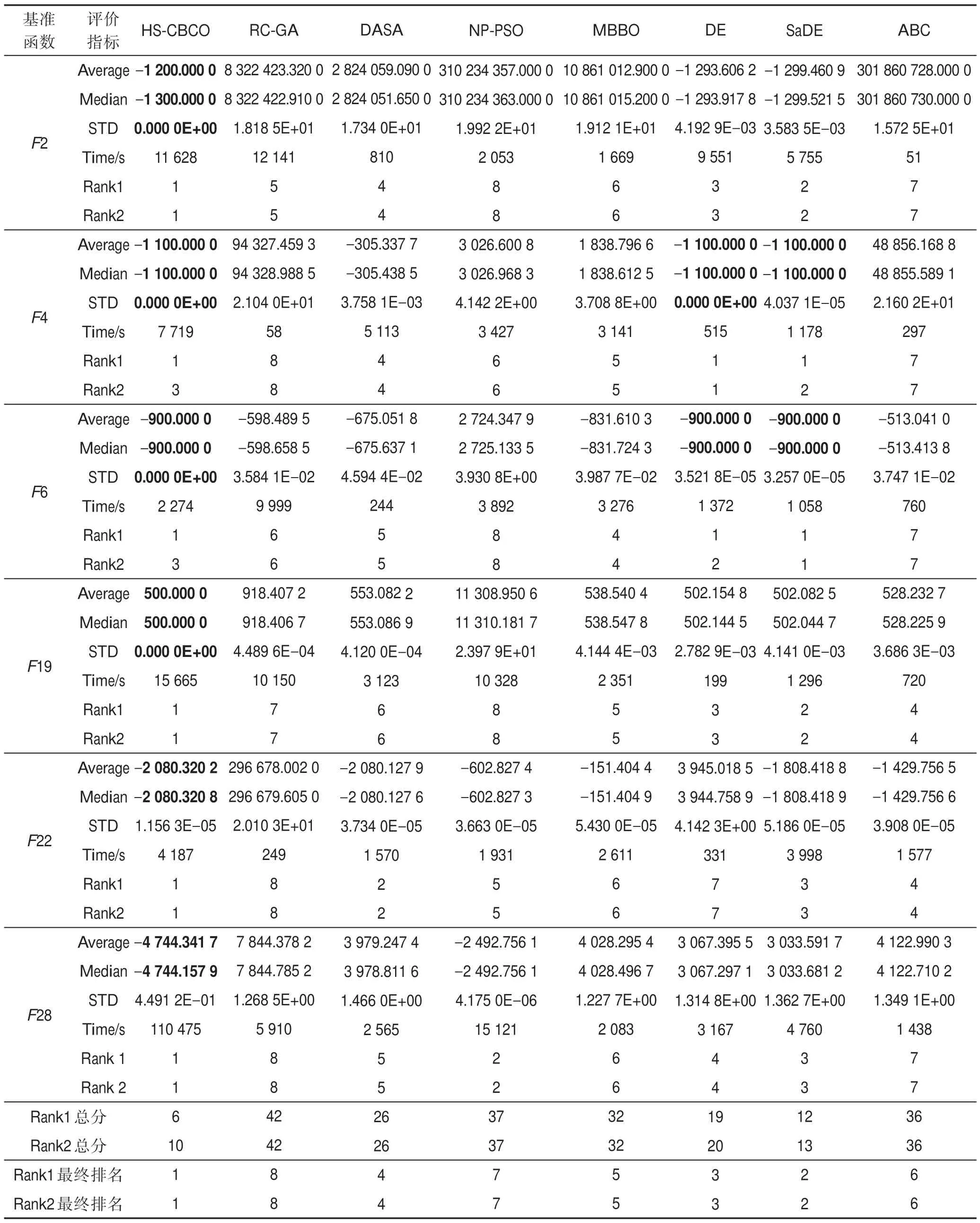
Table 7 Comparison of optimum solutions obtained by each algorithm表7 各算法求解结果的比较

Fig.4 Sample convergence curves图4 样本收敛曲线
6.2 收敛性精度和收敛速度分析
(1)收敛性分析。从定理3 可知,HS-CBCO 算法具有全局收敛性;又从2.5 节知,HS-CBCO 算法具有“步步不差”特性,此表明HS-CBCO 算法的收敛过程不会出现忽大忽小的情形。从图4 所示的样本收敛曲线中的黑实线可知,HS-CBCO 算法的收敛过程与理论分析完全一致。
(2)收敛速度分析。在求解过程中,若HS-CBCO算法经常出现较陡的收敛曲线,说明HS-CBCO 算法的收敛速度较快。从图4(a)~图4(f)的黑实线可知,HS-CBCO 算法收敛较快。
(3)收敛精度分析。在求解后期,若HS-CBCO算法的收敛曲线上升缓慢,且持续时间长,说明HSCBCO 算法提升全局最优解精度的过程十分明确。从图4(a)~图4(f)的后段黑实线可知,HS-CBCO 算法均能获得很高精度的全局最优解。
7 结束语
HS-CBCO 算法具有如下特点:
(1)HS-CBCO 算法依据水平结构竞争-互利群落动力学模型构造,可将生物个体科学地划分成许多种类,从而大幅提升了生物个体的多样性。
(2)HS-CBCO 算法依据水平结构竞争-互利群落动力学模型来确定生物个体数,从而使得生物个体数确定的科学性得到提升,避开了人为确定生物个体数的困扰。
(3)HS-CBCO 算法中运用水平结构竞争-互利群落动力学模型开发出了竞争算子、互利算子、普通影响算子和强烈影响算子。竞争算子和互利算子可实现个体跨种群交换信息,而普通影响算子和强烈影响算子可实现种群内部生物个体之间的信息交换,从而实现生物个体间信息的充分交换。
(4)HS-CBCO 算法的新生算子可适时补充新个体到种群中,而死亡算子可将种群中的虚弱个体适时清除掉,从而大幅提升算法跳出局部陷阱的能力。
(5)HS-CBCO 算法所涉及的参数的绝大部分依据水平结构竞争-互利群落动力学模型来确定,无需人为设置;而需要人为设置的参数却很少,且易于设置。
(6)HS-CBCO 算法的求精能力和探索能力及其两者的协调性均优良。
(7)HS-CBCO 算法的演化过程具有Markov 特性和“步步不差”特性,从而使得该算法具有全局收敛特征。
(8)HS-CBCO 算法具有科学理论作为支撑,易于进行深入分析。
HS-CBCO 算法今后的改进方向如下:
(1)深入研究各算子的动态特征。
(2)深入研究算法在求解过程中各种群的动态特征。
(3)对HS-CBCO 算法进行改进,使之适应复杂水平结构种群竞争、互利环境。
