自主驾驶车辆紧急避障的路径规划与轨迹跟踪控制
2020-04-15邓海鹏麻斌赵海光吕良刘宇
邓海鹏,麻斌,赵海光,吕良,刘宇
(1.吉林大学 汽车仿真与控制国家重点试验室,吉林 长春 130025;2.中国环境科学研究院,北京 100012)
0 引言
紧急避障是车辆实现自主驾驶的关键技术,近年来,国内外学者对自主驾驶车辆的路径规划问题和轨迹跟踪问题做了大量研究。在避障路径规划问题上,许多解决方案已得到成熟应用,如Hilgert等提出的弹性约束理论,以行驶轨迹局部曲率变化率最小为约束条件,对车辆紧急避障路径进行了重新规划[1];Schouwenaars等考虑车辆行驶过程中的安全约束,提出了非结构环境下的滚动时域自主驾驶车辆路径规划[2];Yu等用不同半径圆弧表示不同车速下的行驶路径,并将此触须状规划算法用于未知环境的全局规划[3];张纯刚等结合预测控制理论提出了动态未知环境下的无人小车滚动路径规划[4]。在避障轨迹跟踪问题上,目前应用较为成熟的控制策略和方法有PID控制、滑模控制、自抗扰控制[5]、模糊自适应控制和神经网络控制[6]等。Marino等设计了嵌入视觉导航系统的PID转向控制器,能准确跟踪未知曲率路径[7];Wang等利用鲁棒自适应性滑膜控制器,能同时兼顾车辆的横向控制和对已知轨迹的跟踪[8];Antonelli等[9]和Hajjaji等[10]结合PID方法和模糊控制方法的优势,设计了自适应模糊PID控制器,以改善轨迹跟踪的控制响应性能。然而上述方法无一例外,控制器的自适应程度较低,控制性能过多依赖于环境和参数的设置,并且不能很好地表达和执行自主驾驶车辆在行驶过程中受到的运动学与动力学约束。
模型预测控制应用范围广泛,在车辆电子稳定控制[11]、底盘集成控制[12]、自适应巡航控制[13]等方面都有比较成熟的应用。在自主驾驶车辆的路径重规划和轨迹跟踪方面,模型预测控制(MPC)能根据车辆当前的运动状态预测其未来轨迹[14-17],实现对目标函数的在线滚动优化;同时,MPC能处理车辆在不同行驶工况下的多目标约束问题,可以很方便地将道路前方障碍物信息以不等式约束形式或惩罚函数形式添加到目标函数的求解条件中,以实现车辆的障碍物避让功能[18]。
本文设计了双层MPC紧急避障控制器。在路径规划层引入避障功能函数,综合考虑避障函数权重和临时路径与全局路径的偏差权重,规划出紧急避障轨迹。在轨迹跟踪层,提出以参考轨迹和车辆航向角偏差作为控制参考量的轨迹跟踪转向控制算法,采用线性时变MPC计算满足车辆动力学约束的前轮转向角最优解。
1 车辆模型
1.1 车辆点质量模型
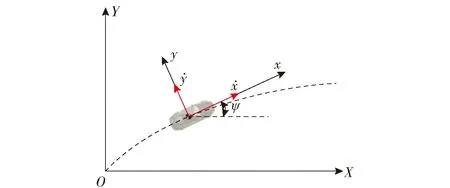
图1 车辆点质量模型Fig.1 Point mass model of autonomous vehicle
在参考坐标系下,车辆的点质量运动学模型[15]表示为
(1)
(2)
(3)
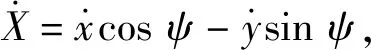
(4)
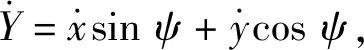
(5)

1.2 车辆动力学模型
地面行驶的车辆通常考虑纵向、横向和横摆3个维度的运动。为了使车辆快速且准确地跟踪临时路径,需要建立精确的车辆动力学模型[19](见图2),以此做为线性时变模型预测控制(LTV-MPC)的基础,提高车辆的操纵稳定性。图2中:δ为车辆前轮转向角;β为车辆质心侧偏角;Flf和Flr为前、后轮胎受到的纵向力;Fcf和Fcr为前、后轮胎受到的侧向力;αf和αr为车辆前、后轮侧偏角。
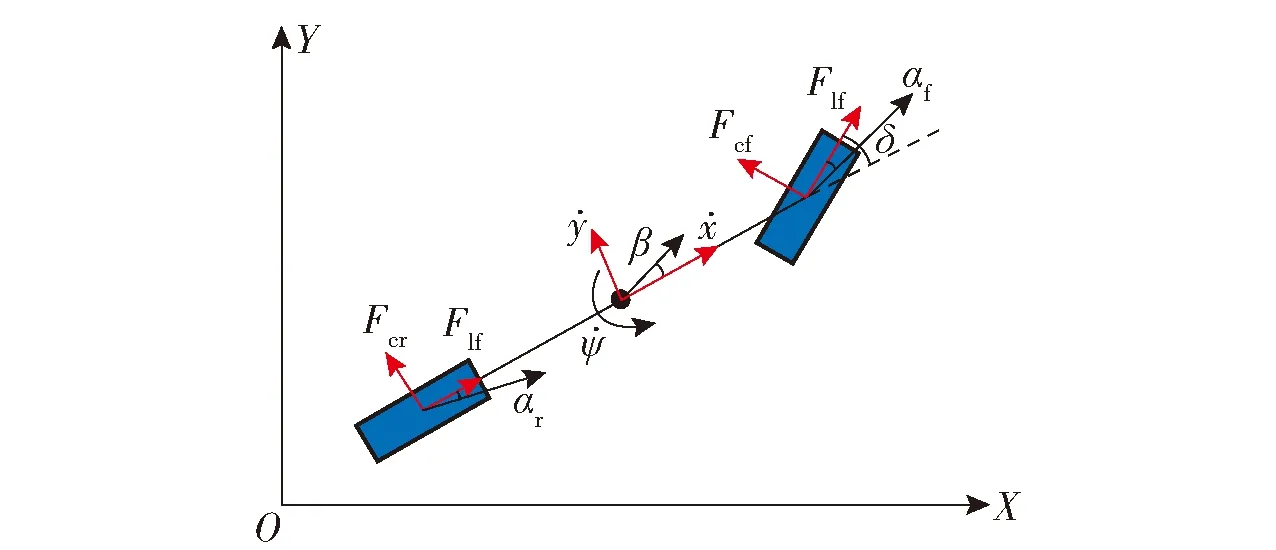
图2 车辆动力学模型Fig.2 Dynamic model of autonomous vehicle
如图2所示,考虑车辆横向和横摆2个维度的运动,假设车辆左右受力完全对称且δ足够小,根据牛顿第二定律建立的车辆动力学方程如下:
(6)
(7)
(8)

1.3 轮胎模型
轮胎受到的竖直载荷、纵向力、横向力以及回正力矩对车辆的安全性和操纵稳定性至关重要。Pacejka用经验公式拟合轮胎试验数据后提出的魔术轮胎模型能正确描述轮胎纵向力、侧向力等与滑移率和侧偏角之间的关系[20]。魔术轮胎模型的一般表达式为
Y(x)=Dsin{Carctan[Bx+Bsh-
E(Bx+Bsh-arctan(Bx+Bsh))]}+sv,
(9)
式中:Y(x)为轮胎受力模型;B为刚度因子;C为形状因子;D为峰值因子;E为曲率因子;sh为轮胎水平偏移;sv为轮胎垂直偏移。
当自变量x表示轮胎纵向滑移率时,输出量Y为轮胎的纵向力;当x表示轮胎侧偏角时,Y为轮胎侧向力。根据(9)式,可得轮胎纵向力随滑移率s的变化曲线如图3所示,轮胎侧向力随轮胎侧偏角的变化曲线如图4所示。
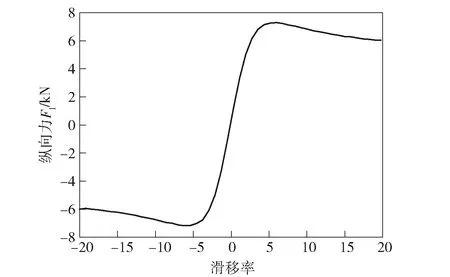
图3 轮胎纵向力与滑移率关系曲线Fig.3 Longitudinal tire force vs.slip rate

图4 轮胎侧向力与侧偏角关系曲线Fig.4 Lateral tire force vs.slip angle
纵向滑移率和轮胎侧偏角的变化范围通常较小,因此可以将轮胎魔术公式用线性表达式近似[19],线性化处理的轮胎纵向力和侧向力可以表示为
F1=C1s,
(10)
Fc=Ccα,
(11)
式中:C1为轮胎纵向刚度;Cc为轮胎侧向刚度。当车辆侧向加速度ay≤0.4g时,可认为(10)式和(11)式线性化处理的轮胎纵向力和侧向力具有较高的拟合精度[21-22]。
车辆前、后轮侧偏角的近似表达式为
(12)
(13)
(12)式和(13)式代入(10)式和(11)式,可以得到前、后轮纵向力和侧向力为
Flf=Clfsf,
(14)
Flr=Clrsr,
(15)
(16)
(17)
式中:Clf为前轮纵向刚度;Clr为后轮纵向刚度;sf为前轮滑移率;sr为后轮滑移率;Ccf为前轮侧向刚度;Ccr为后轮侧向刚度。
上述简化处理的轮胎模型代入(6)式~(8)式中,结合车辆在参考坐标系下的位置信息(4)式和(5)式,即可得到基于前轮小角度转向和线性轮胎模型的车辆动力学模型如下:
(18)
(19)
(20)
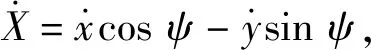
(21)
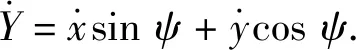
(22)
2 路径规划与跟踪控制器设计
2.1 路径规划器设计
为使路径二次规划能适应不同的避障函数形式,上层控制器采用非线性形式的模型预测控制。使用欧拉公式将(1)式~(5)式离散化,得到车辆状态量的差分方程如下:
(23)
(24)
(25)
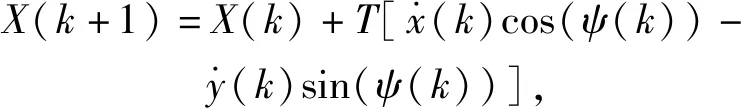
(26)
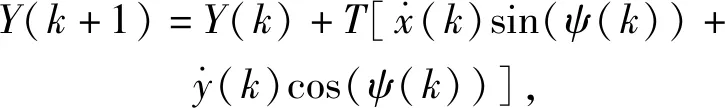
(27)
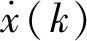
η(k+i|t)=Fi[η(k|k),ay(j)],
i=1,2,…,Np,j=1,2,…,Nc,
(28)
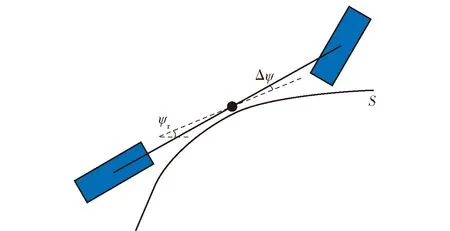
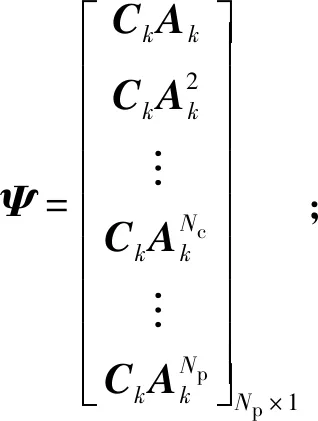
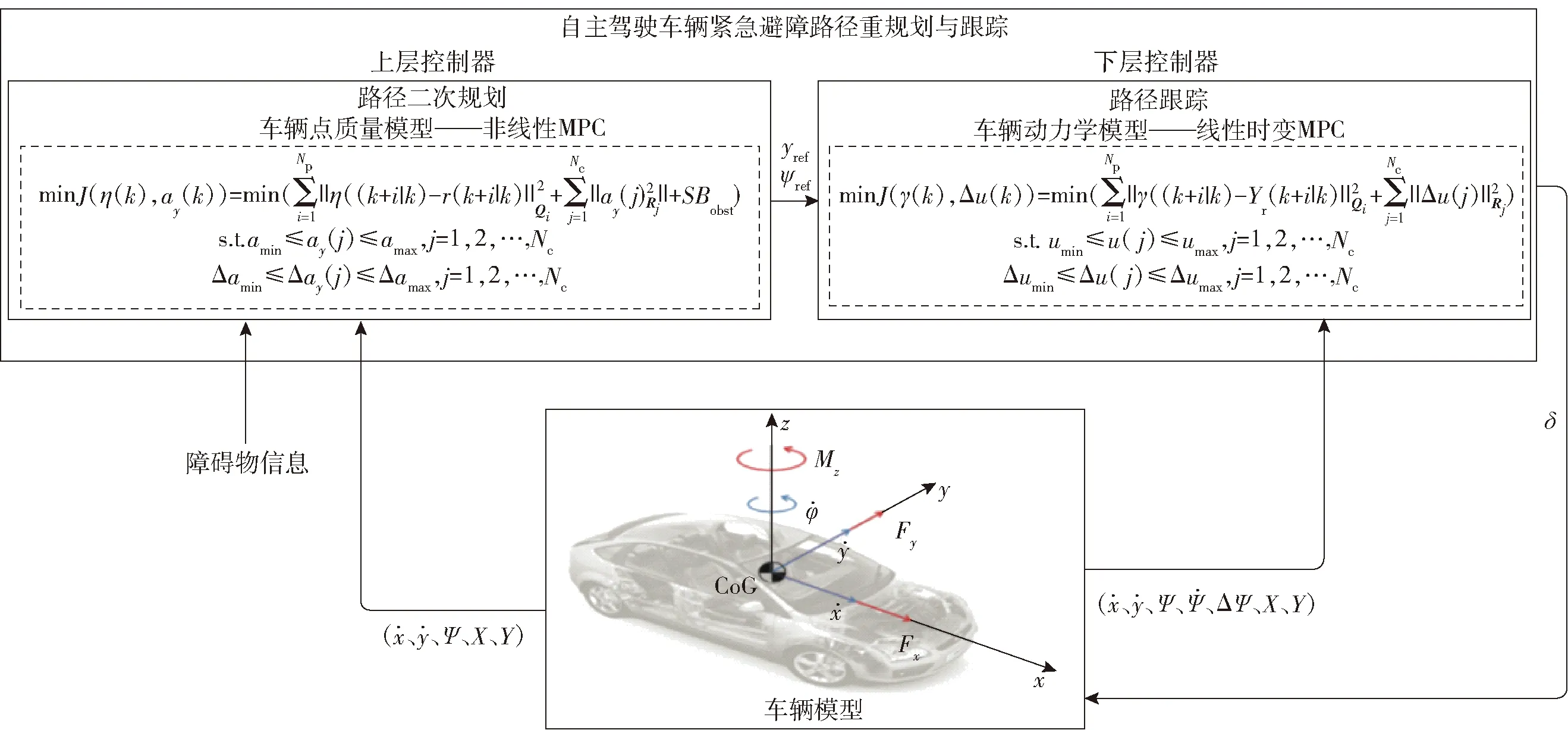
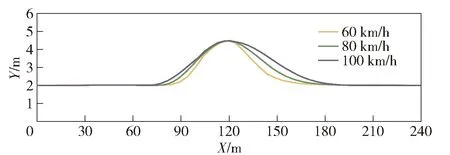
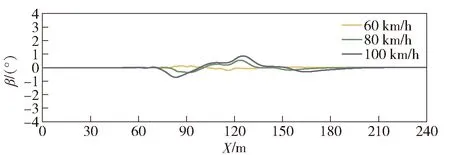
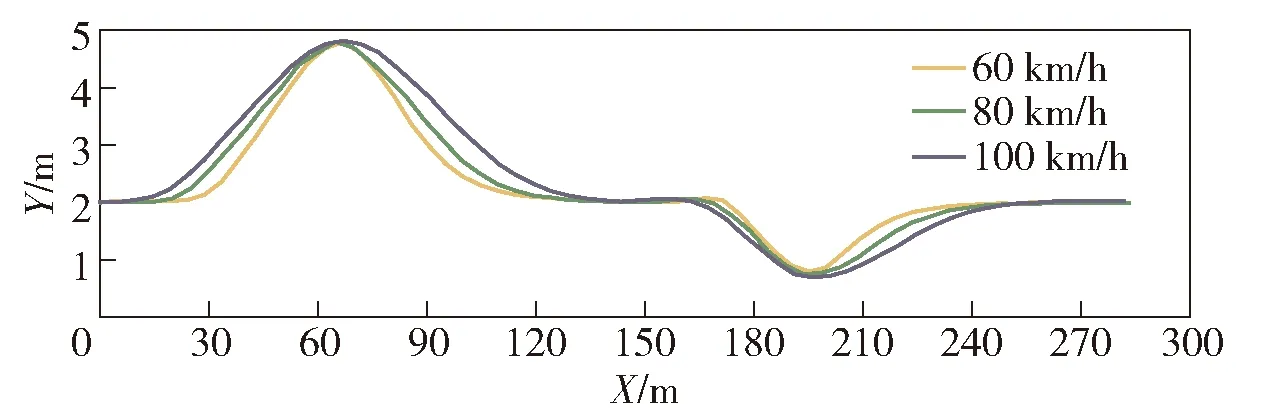
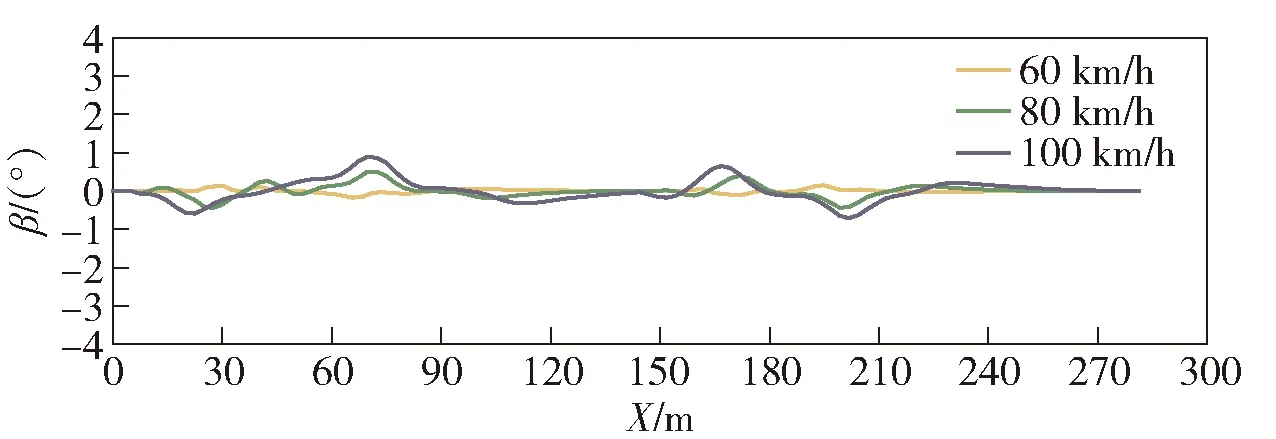
式中:Fi(·)为差分方程的函数表达形式;η(k|k)为5个车辆初始状态量。为减少计算量、增强系统的实时性,本文取控制步长Nc=3.在控制步长外(Nc (29) 综上所述,可得非线性模型预测控制(NMPC)预测时域Np内的预测表达式为 (30) 式中:η(k+i|k)表示用k时刻车辆状态预测k+i时刻车辆状态。 考虑到自主驾驶车辆的避障路径要求控制器尽可能缩小临时路径与全局参考路径偏差,同时实现自主驾驶车辆对障碍物的避让,因此本文设计的非线性模型预测控制的目标函数形式为 (31) s.t.amin≤ay(j)≤amax,j=1,2,…,Nc, (32) Δamin≤Δay(j)≤Δamax,j=1,2,…,Nc. (33) 式中:r(k+i|k),i=1,2,…,Np为给定的全局参考路径;Bobst为避障功能函数;Qi为预测时域内(k+i,i=1,2,…,Np)控制输出的权重矩阵;Rj为控制时域内(j=1,2,…,Nc)控制输入的权重矩阵;S为避障功能函数的权重系数。 避障功能函数通过车辆与障碍物之间的距离和当前车速计算函数值的大小,如(34)式所示,自主驾驶车辆到障碍物的距离越近,车速越大,则函数惩罚值越大。 (34) 式中:xi、yi为障碍物在惯性坐标系下的位置坐标;X0、Y0为车辆当前位置坐标;ε为非0正数(本文取0.001以避免分母为0)。从避障功能函数惩罚值示意图(见图5)可以看出,当车辆接近障碍物时,惩罚数值急剧增大,使得目标函数minJ(η(k),ay(k))的求解远离障碍物的车辆坐标X、Y,减小避障惩罚函数的罚值,规划出避开障碍物的行驶路径。当车辆与障碍物处于安全距离时,避障功能函数惩罚值极小,此时目标函数正常跟踪全局参考路径。 图5 避障功能函数惩罚值示意图Fig.5 Penalty value of obstacle avoidance function 求解得出满足约束条件的控制输入量ay(1)、ay(2)和ay(3),根据(25)式和(27)式,即可得到避障路径的航向角和车辆纵向位置坐标。 由于求解得出的新轨迹是预测时域内的离散点,控制层很难根据离散点参考轨迹完成跟踪任务,需要对规划轨迹的离散数据点进行拟合。为得到较高的曲线拟合精度、减小路径跟踪误差,本文选用四次多项式对预测轨迹离散点拟合。将规划路径的纵坐标yr和车辆航向角ψr随车辆纵向位移X的变化曲线传递至轨迹跟踪层,作为下层轨迹跟踪控制器的参考值,yr和ψr的传递形式为 yr=p0+p1X1+p2X2+p3X3+p4X4, (35) ψr=q0+q1X1+q2X2+q3X3+q4X4, (36) 式中:p0、p1、p2、p3和p4分别为参考轨迹拟合系数;q0、q1、q2、q3和q4分别为参考航向角ψr拟合系数。 下层轨迹跟踪控制器根据车辆动力学模型实时调整车辆和参考轨迹之间的位姿偏差。本文跟踪器以参考轨迹yr和车辆的航向角偏差Δψ作为轨迹跟随的控制参考量,以前轮偏转角δ作为转向控制输入量。由于NMPC对于实时系统存在局限性,故设计线性时变预测模型求解满足车辆动力学约束的最优前轮偏转角。如图6所示,车辆航向角偏差为参考轨迹航向ψr和车辆实际航向之差,计算公式如(37)式所示: Δψ=ψr-ψ. (37) 图6 车辆航向角偏差示意图Fig.6 Deviation of vehicle yaw angle 结合车辆动力学模型(18)式~(22)式和航向角偏差(37)式,可将轨迹跟踪器的设计表示为如下状态空间形式: (38) yc=Cχ, (39) (38)式中状态变量的非线性模块难以满足轨迹跟踪控制器实时性的要求,且在计算过程中容易引入非线性约束增加计算复杂程度,因此需要对(38)式进行线性化处理,以获得线性时变预测模型。将(38)式在工作点(χ0,u0)处以泰勒公式展开,忽略高阶项,得 (40) 式中:u0为工作点的控制输入量;χ0为工作点的状态变量, (41) (41)式与(40)式相减,得到 (42) (42)式离散化,可得状态变量表达式为 χ(k+1)=Aχ(k)+Bu(k)+d(k), (43) 为减小静态误差,将(43)式中的控制量改写成控制增量[17]的形式: ξ(k+1|k)=Akξ(k|k)+BkΔu(k|k)+dk(k), (44) γ(k|k)=Ckξ(k|k), (45) 迭代(45)式,可得预测时域内Np输出量的表达形式为 (46) 结合车辆动力学约束条件,得到线性模型预测控制目标函数如下: (47) s.t.umin≤u(j)≤umax,j=1,2,…,Nc, (48) Δumin≤Δu(j)≤Δumax,j=1,2,…,Nc, (49) 式中:Δumax(k)为控制增量上边界;Δumin(k)为控制增量下边界。 综合路径规划器和轨迹跟踪器的设计思路得到图7所示的双层MPC紧急避障控制器逻辑结构,其中,上层控制器根据前方道路障碍物信息和车辆当前运动状态进行路径二次规划,下层控制器接收临时规划的轨迹信息和车辆当前运动状态进行轨迹跟踪。 图7 路径规划与轨迹跟踪控制逻辑图Fig.7 Control model of path planning and tracking 为了验证双层MPC紧急避障控制器的有效性,利用汽车动力学仿真软件Carsim和MATLAB/Simulink联合仿真平台测试自主驾驶车辆的避障效果。仿真车辆模型参数如表1所示。 表1 车辆基本参数Tab.1 Essential parameters of autonomous vehicle 3.1 平直路面避障效果分析 全局参考路径为一段长240 m的直行路段,在自主驾驶车辆正前方有一台故障车辆,分析不同车速下控制器对该静止故障车的避障性能。 根据道路前方故障车辆位置信息,双层MPC紧急避障控制器综合考虑车辆的行驶操纵稳定性约束条件自动规划出最适合车辆当前运动状态的轨迹。在平直城市路面,自主驾驶车辆的避障效果如图8所示。 图8 避障轨迹车辆移动幻影示意图Fig.8 Moving trajectory during obstacle avoidance 图9所示为车辆速度分别为60 km/h、80 km/h和100 km/h时车辆的行驶轨迹。从图9中可以看到,车速为60 km/h时,自主驾驶车辆在85 m处开始响应路径规划层的避障功能,车速越大,避障功能响应时刻提前,车速为80 km/h和100 km/h时控制器分别在80 m和75 m处做出避障决策。这是因为本文设计的避障功能函数考虑了本车速度对二次路径规划的影响,车速越大、避障功能函数的惩罚值越大,规划控制器以牺牲规划路径与全局参考路径(Y=2 m)的跟踪精度为代价增大车辆与障碍物之间的距离,避障控制策略符合高速行驶车辆提前避让的驾驶行为。 图9 不同行驶速度下车辆轨迹Fig.9 Moving trajectories of vehicle at various velocities 从图9中也可以看出,不同车速下车辆的侧向位移最大偏差相同。图10和图11所示分别为不同车速下车辆的航向角偏差和质心侧偏角,仿真结果显示,在平直路段车辆的质心侧偏角和航向角偏差都控制在一个较小的范围内(|Δψ|<2.5°,|β|<1°),表明车辆在紧急避障过程中行驶稳定,设计的避障控制器对车速变化具有很强的适应性。 图10 不同行驶速度下车辆航向角偏差Fig.10 Deviation of vehicle yaw angles at various velocities 图11 不同行驶速度下车辆质心侧偏角Fig.11 Side-slip angles of vehicle at various velocities 针对行车过程中道路障碍物出现的随机突发性,本文建立贴近实际情况的自主驾驶车辆多车连续避障实验场景(在道路前方50 m处存在多辆需避让的目标车辆,在道路前方190 m处存在逆向行驶的越界车辆)。 根据前方目标车辆和逆向行驶车辆的位置信息,本文设计的双层MPC紧急避障控制器的多车避障效果和会车避让效果如图12和图13所示。 图12 多目标避障效果示意图Fig.12 Moving trajectory of vehicle during multi-obstacles avoidance 图13 逆向越界车辆避障效果示意图Fig.13 Moving trajectory of vehicle during multi-obstacles avoidance 图14所示为60 km/h、80 km/h和100 km/h不同车速下自主驾驶车辆的多车连续避障行驶轨迹。对于正前方的目标车辆,随着行车速度的增大,自主驾驶车辆分别在25 m、20 m和15 m处响应控制器的避障功能,避障最大侧向位移约为3 m;对于逆向驶来的越界车辆,随着车速增加,自主驾驶车辆分别在175 m、170 m和165 m处响应控制器的避障效果,避障最大侧向位移约为1.2 m.从避障轨迹来看,车速越大,车辆的避障响应时刻越早。 图14 不同行驶速度下自主驾驶车辆连续避障轨迹Fig.14 Moving trajectories of vehicle at various velocities during multi-obstacles avoidance 图15和图16所示分别为60 km/h、80 km/h和100 km/h不同车速下多车连续避障时车辆质心侧偏角和航向角偏差的变化情况。实验结果显示,在多目标连续避障过程中,车辆最大质心侧偏角|β|均不超过1°,表明MPC路径规划控制策略能保证车辆较高的行驶稳定性;车辆的最大航向角偏差|Δψ|均不超过2.5°,表明对于多目标连续避障情况,双层MPC紧急避障控制器同样具有很好的控制效果。 图15 车辆连续避障质心侧偏角Fig.15 Side-slip angles of vehicle during multi-obstacles avoidance 图16 车辆连续避障航向角偏差Fig.16 Deviation of vehicle yaw angles during multi-obstacles avoidance 本文根据车辆点质量模型、车辆运动学模型和魔术轮胎模型设计了双层MPC紧急避障控制器,通过Carsim和MATLAB/Simulink联合仿真平台验证了紧急避障控制器对车辆速度变化以及对多目标连续避障均具有很好的控制效果。得到主要结论如下: 1)紧急避障控制策略对低速(60 km/h)、中速(80 km/h)、高速(100 km/h)行驶车辆有很强的适应性,高速行驶时车辆的最大质心侧偏角不超过1°,最大航向角偏差不超过2.5°. 2)在由道路前方目标车辆和逆向驶来的越界车辆组成的多车连续避障实验场景中,自主驾驶车辆的质心侧偏角β和航向角偏差Δψ均控制在合理的范围内。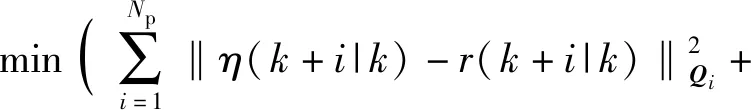

2.2 轨迹跟踪器设计
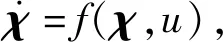
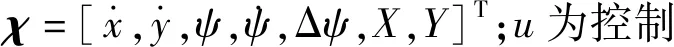
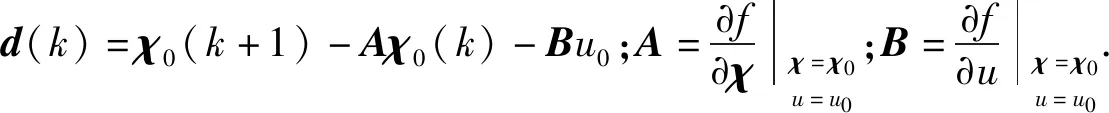
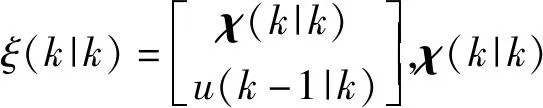
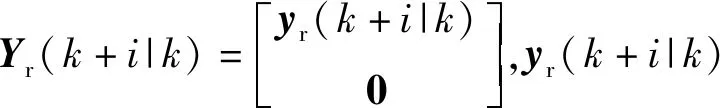
2.3 紧急避障控制器结构
3 仿真结果与分析



3.2 多目标连续避障效果分析



4 结论
