利用卡尔曼滤波和人工神经网络相结合的油藏井间连通性研究

刘 巍，刘 威，谷建伟，姬长方，隋顾磊

（中国石油大学（华东）石油工程学院，山东青岛 266580）

中国大部分水驱油藏均已进入高含水、低水驱效率阶段，油藏井间连通性的定量研究，准确认清注入水的流动方向、对于制定合理的开发调整方案和提高水驱油藏采收率具有重要意义。井间连通性分析方法主要分为静态分析法和动态分析法2大类。其中静态分析法主要包括：地球化学方法［1-2］、干扰试井分析方法［3-4］和示踪剂测试方法［5］等。根据注采数据反演井间连通状况而衍生的动态分析法主要包括：Spearman相关关系分析方法［6］、多元线性回归分析方法［7］、电容模型分析方法（CRM）［8］、系统分析模型方法［9-10］、多井采液指数模型分析方法［11］、集合卡尔曼滤波模型分析方法［12］和神经网络模型分析方法［13-14］。静态分析法测试成本高，测试周期长。动态分析法具有数据获取方便、资料丰富和成本低等优势，已成为井间连通性研究的重要方法［15-16］，其中，相关关系分析模型及多元线性回归模型不能准确反映注采系统的连通状况；电容模型、系统分析模型和多井采液指数模型等的建立及推导过程较为复杂，且模型参数求解耗时长、求解难度大。现有的基于人工神经网络的井间连通性分析方法不能准确考虑注入水在地层中传播的时滞性。为此，笔者结合卡尔曼滤波器［17］、人工神经网络模型以及构建的非线性扩散滤波器，建立了能综合考虑注入信号存在噪声和传播时滞性的井间连通模型分析方法。模型建立过程简便，计算效率较高，通过具有典型地质特征油藏和实际非均质油田的井间连通性计算结果，验证了方法的准确性和有效性。

1 卡尔曼滤波原理

卡尔曼滤波（简称KF）由匈牙利数学家卡尔曼于1960 年提出。其基本思想是利用系统动态信息的前一时刻的估计值和当前时刻的观测值来更新模型和状态变量的估计，设法去掉噪声的影响，求取当前时刻的最优估计值，如此循环实现自回归［17］。其算法结构主要由时间更新方程和状态更新方程2部分组成。

1.1 时间更新方程

时间更新方程用于及时向前推算当前状态变量和误差协方差估计的值，以便为下一个时间状态构造先验估计。其方程式为：

1.2 状态更新方程

状态更新方程将先验估计和新的测量值结合以构造改进的后验估计，基于当前时刻的预测结果，结合测量值，便可得到当前时刻的最优估计值。其方程式为：

2 注采系统连通模型的建立

神经网络具有较强的非线性逼近特性及自学习、自组织的能力，是模拟和建立注采系统非线性相关关系的有利工具。笔者通过搭建的人工神经网络（简称ANN）建立生产井与周围注水井的连通关系模型，利用历史注采数据对模型进行训练和优化，实现人工神经网络模型对注采系统的自适应模拟，进而获取注采数据中的井间连通信息。

2.1 人工神经网络模型的搭建

根据油田实际情况，以整个区块或某个井组注水井的注水速率为影响因素，并作为ANN 模型的输入参数；以生产井产液量为目标参数，并作为ANN模型的输出项，建立具有5个输入节点（对于实际油田案例输入节点为6 个）和1 个输出节点的ANN 模型。确定其初始的隐藏层数为1 层，节点为15 个，并在［-1，1］区间对网络的权重系数随机初始化。

2.2 学习样本的构建

分别建立均质、各向异性、封闭断层和高渗透带的4 种典型油藏模型，参考油田现场的实际注水数据，应用油藏数值模拟得到各个油藏的注采数据，并给数据增加1 个符合高斯分布的扰动误差构成最终的学习样本。对于实际油藏22ZY 井区学习样本的构建，则是选取现场观测和记录的2013年12月1 日至2019 年5 月1 日注水井的日注水量和生产井的日产液量，均以8∶2 的比例划分样本数据为训练集和测试集，分别用于ANN模型的训练和验证。

2.3 数据去噪和时滞特性

油田现场监测到的实际注采数据均存在一定的干扰和噪声，对最终的分析结果会造成较大误差。通过卡尔曼滤波实现对注采数据的去噪处理，提高井间连通性分析的准确性（图1）。

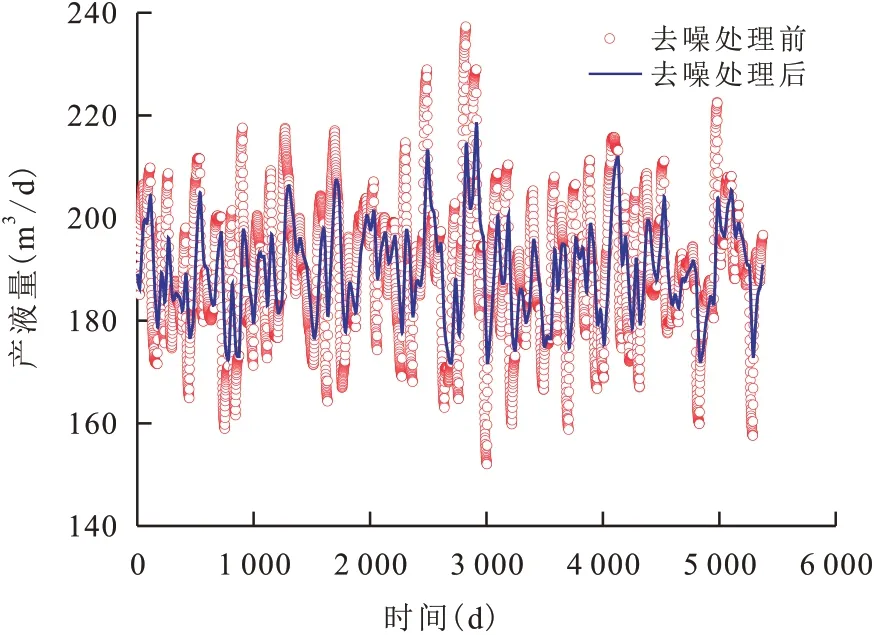
图1 注采数据去噪处理前后对比曲线Fig.1 Comparison of injection-production data curves before and after denoising

实际油藏中，注入水在地层中传播存在时滞特性和衰减特性，注入量的变化不会立即引起生产井产液量的改变。因而基于压降叠加原理，构建非线性扩散滤波器［7］，对注入量进行预处理，来考虑传播过程中存在的滞后现象，使得反演结果更符合油藏实际情况。注入量在油藏中的滞后可以等效为当前时刻生产井的产液量不仅与注水井的注入量有关，还与之前的注入状态有关。因而在某时间步，生产井的产液量响应可以看作是一系列注入脉冲在该时间步引起的响应之和。根据压降叠加原理，地层中任意点的压降值等于各井单独工作时在此点产生压降值的代数和，构建以下非线性扩散滤波器，将注入脉冲的响应离散成时间序列上的一系列脉冲之和（本文离散成n0个月），离散后各时间步注入量响应所占比重［7］：

利用滤波系数修正原始注入量，得到考虑注入信号时滞特性和衰减特性的有效注入量为：

采用归一化方法，将各个注水井的注入参数统一到［0，1］区间，使影响数据质量的各种系统误差降至最低，避免各参数间的量纲差异而造成较大误差。归一化方法的计算公式为：

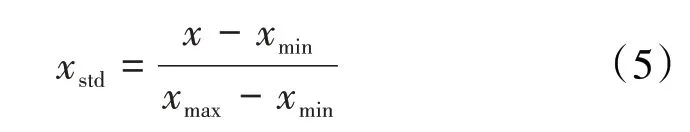
2.4 模型训练和参数优化

ANN 结构优化的目的主要在于选择合适的隐藏层数、节点个数和激活函数，采用网格搜索算法，在测试集基础上，对ANN 训练和预测效果进行反复测试和验证，进而确定最优的隐藏层数和节点个数，建立3 层ANN 模型（图2），该模型包括5 个输入层，25 个隐藏层节点和1 个输出节点。采用梯度学习算法，在训练集上实现ANN 权重系数的学习和优化，最终建立注采系统连通模型。

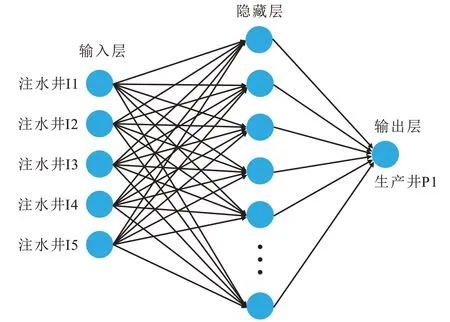
图2 ANN模型示意Fig.2 Architecture of ANN model

2.5 预测结果分析和评价

注采系统的井间连通性计算结果的分析评估，主要包括决定系数和不对称系数2个指标。决定系数的定义式为：

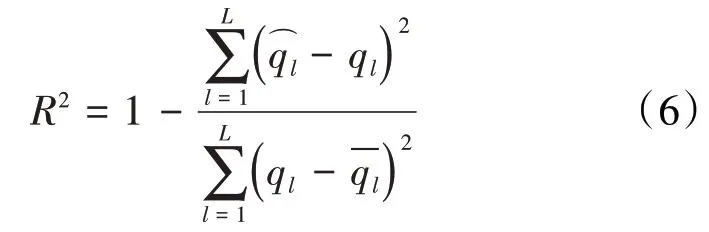
决定系数越大，说明拟合程度越好，ANN 模型的结构和权重系数越合理，通过ANN 模型建立的注采关系越准确可靠。

在均质油藏中的注采井间连通状况具有明显的对称性。对于五注四采模型，将连通性分成3组：a组表示注水井角井与相邻生产井连通系数；b组表示注水井角井与非相邻的生产井连通系数；c组表示中央注水井和相邻生产井连通系数。通过计算不对称系数（不对称系数越小，动态连通性反演结果越好）来评估模型井间连通性的反演结果［7］，其定义式为：

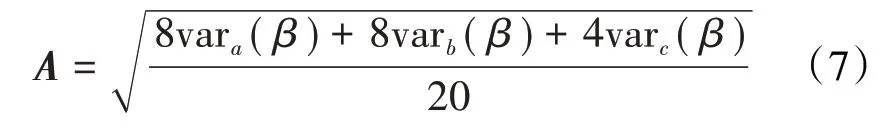
3 井间连通系数的计算

基于建立的ANN 模型，根据敏感性分析法则［18］，求取生产井对各注水井的敏感系数，用于表征生产井与注水井的连通状况。敏感系数越大，连通性越好［14］。以ANN 模型为例，说明敏感性计算式的推导过程。

由n个输入节点，m个隐藏层节点和p个输出节点构成3 层ANN 模型，各层上的值用向量可以表示为：

输出节点对输入节点的敏感性可表示为：

根据链式求导法则，基于ANN 建立的相互连接单元，敏感性公式可进一步表示为：

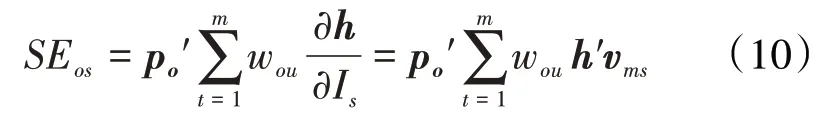
利用（10）式可以得到单个样本的敏感性关系，为了表征注采井间的总体连通性，需要计算每个样本数据敏感系数的均方根，定义式为：

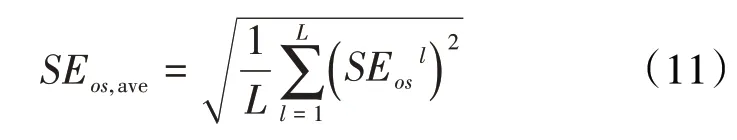
4 应用实例

4.1 典型油藏井间连通性分析

基于建立的井间连通性分析方法，分别对均质、各向异性、包含封闭断层和具有高渗透率带的4种典型油藏模型的注采系统进行分析。油藏模型的平均有效厚度为2.5 m，网格长度及宽度均为20 m，共45×45×1=2 025 个网格。采用五点法井网，建立五注四采模型。结合油田现场的实际注水状况，构建注水井（I1，I2，I3，I4，I5）的注水数据（图3）。

4.1.1 均质油藏

均质油藏各向渗透率为60 mD。利用数值模拟计算得到各生产井P1，P2，P3，P4 的产液量，基于注采数据对建立的ANN 模型进行训练，得到各生产井产液量的预测值与实际值的拟合效果，由（6）式得到决定系数分别为0.957，0.958，0.959，0.959。从图4 可以看出，建立的ANN 模型准确模拟了注采系统的井间连通状况。基于此模型进行敏感性分析得到各生产井与周围注水井之间的连通系数（表1）。由（7）式计算不对称系数为0.045，说明计算得到的井间连通性具有较好的对称性。

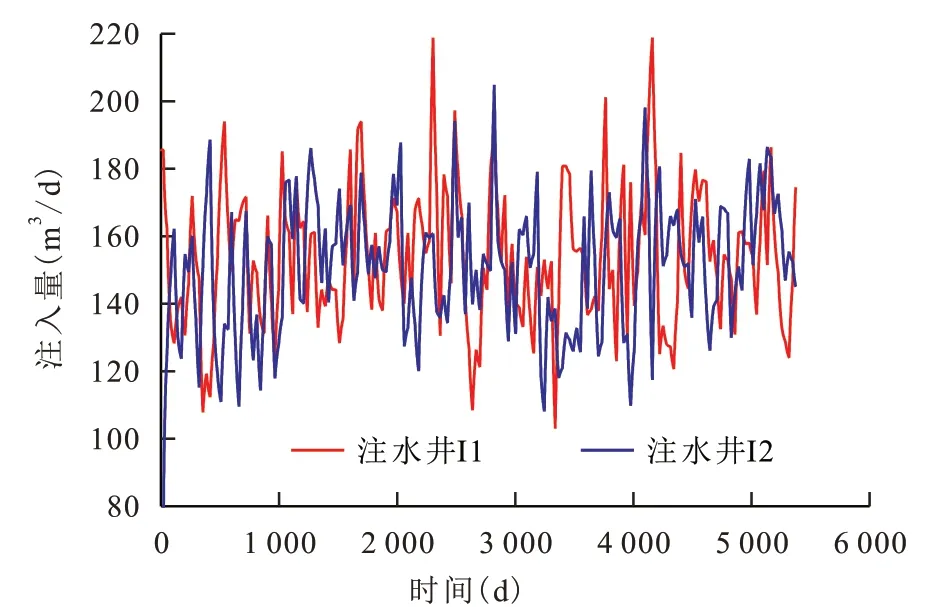
图3 注水井的动态注入数据Fig.3 Water injection rates of injectors

为了更直观表征井间连通系数及均质油藏的对称性，绘制井间连通关系（图5）。从图5a 可以看出，均质油藏的注采连通关系具有较好的对称性，计算结果与均质油藏的实际渗流特征相符。

4.1.2 各向异性油藏

对于各向异性油藏，横向渗透率与纵向渗透率比值为10。从该油藏的井间连通系数计算结果（表2）和相应的注采井间连通关系（图5b）可以看出，横向上所有注采井间的连通系数明显大于纵向上的连通系数。

4.1.3 包含封闭断层油藏

包含封闭断层油藏是在生产井P2 与注水井I4之间有一倾斜的封闭断层。从该油藏的井间连通系数计算结果（表3）和相应的注采井间连通关系（图5c）可以看出，位于断层两侧的注水井和生产井之间的连通系数几乎为0，互不连通，与包含封闭断层油藏的渗流特征相符。

4.1.4 具有高渗透带油藏

具有高渗透带油藏是在模型的横向和纵向分别存在渗透率为180 mD 的高渗透通道。从该油藏的井间连通系数计算结果（表4）和相应的注采井间连通关系（图5d）可以看出，存在高渗透通道的注水井I1和生产井P1之间及注水井I3和生产井P4之间的井间连通系数明显大于其余方向和其他注采井之间的连通系数，其计算结果符合油藏的实际渗流特征。

4.2 实际非均质油藏

图4 基于ANN模型的单井产液量预测结果Fig.4 Comparison of fluid production rates of single well predicted by ANN model and actual value

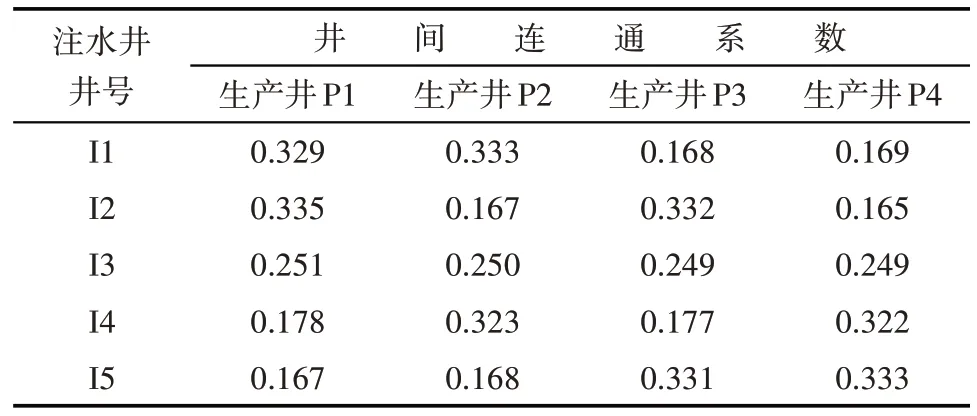
表1 均质油藏井间连通系数计算结果Table1 Interwell connectivity of homogeneous reservoirs

为了测试方法的实际应用效果，选取某油田22ZY 井区注采数据进行连通性分析。该井区有6口注水井（22ZY-1，22ZY-2，22ZY-3，22ZY-4，22ZY-5，22ZY-6）和2 口生产井（22ZY-11，22ZY-12）。基于ANN 模型建立的注采关系系统预测生产井22ZY-11 和22ZY-12 的产液量，绘制注采井间连通关系（图6）。与实际产液量对比，评估模型的预测性能，得到相对误差分别为1.34%和1.56%，决定系数分别为0.91和0.94。

图5 典型油藏井间连通关系Fig.5 Interwell connectivity in representative reservoirs

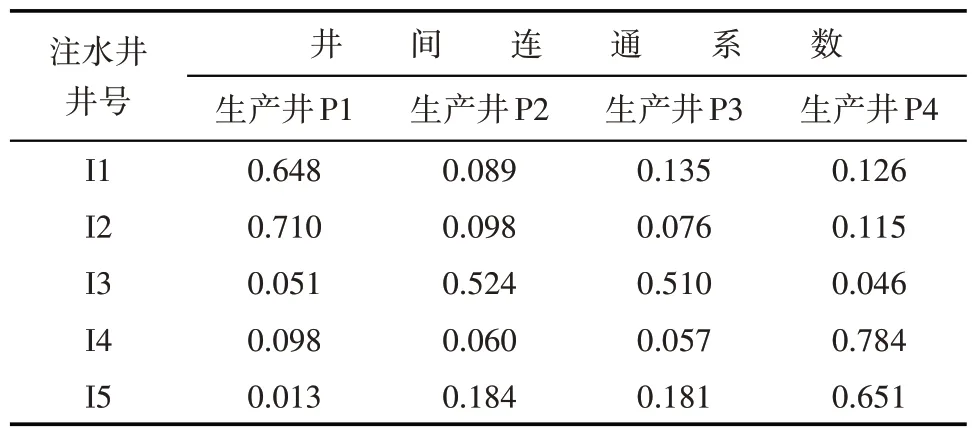
表2 各向异性油藏井间连通系数计算结果Table2 Interwell connectivity factors in anisotropic reservoir

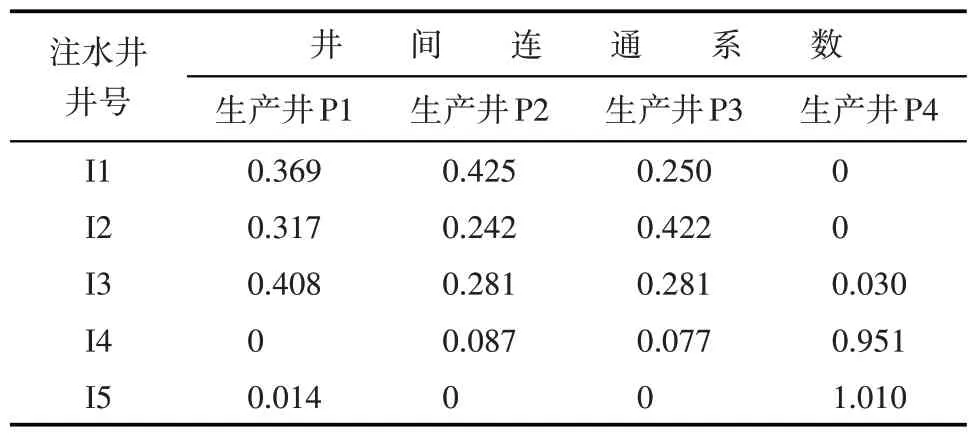
表3 包含封闭断层油藏井间连通系数计算结果Table3 Interwell connectivity factors in reservoir with closed fault

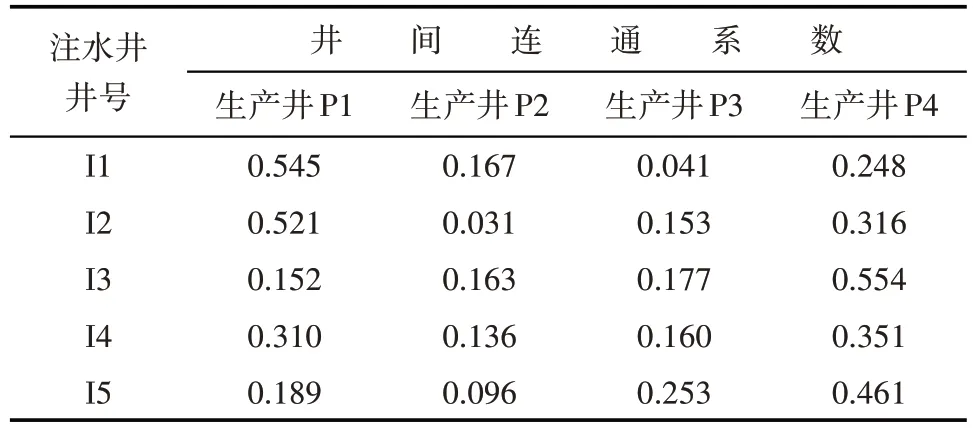
表4 具有高渗透带油藏井间连通系数计算结果Table4 Interwell connectivity factors in reservoirs with high permeability zone

图6 某油田22ZY井区注采连通关系Fig.6 Interwell connectivity of injection and production in well block 22ZY of certain oilfield

由图6 可见，生产井22ZY-11 与注水井22ZY-5和22ZY-6 不连通，且注水井22ZY-3，22ZY-4 与22ZY-11 的连通性相等；生产井22ZY-12 与注水井22ZY-1，22ZY-2 几乎不连通，与注水井22ZY-5 和22ZY-6 的连通性相等。该分析结果与油田现场的示踪剂测试结果完全一致，证明了该方法的有效性。

从KF-ANN 与ANN 模型的井间连通性分析结果（表5）对比可以看出：直接用ANN 模型分析注采井间的连通性时，由于数据中存在的噪声污染和误差，使得模型不能准确地反映油藏的地质特征，造成分析结果不准确。例如生产井22ZY-11 与注水井22ZY-5 应该不连通，同样生产井22ZY-12 与注水井22ZY-1 也不连通，可计算结果却表明均存在连通性，与实际测量结果不符。说明基于KF 数据降噪的ANN 模型更适合用于油藏井间连通性分析。

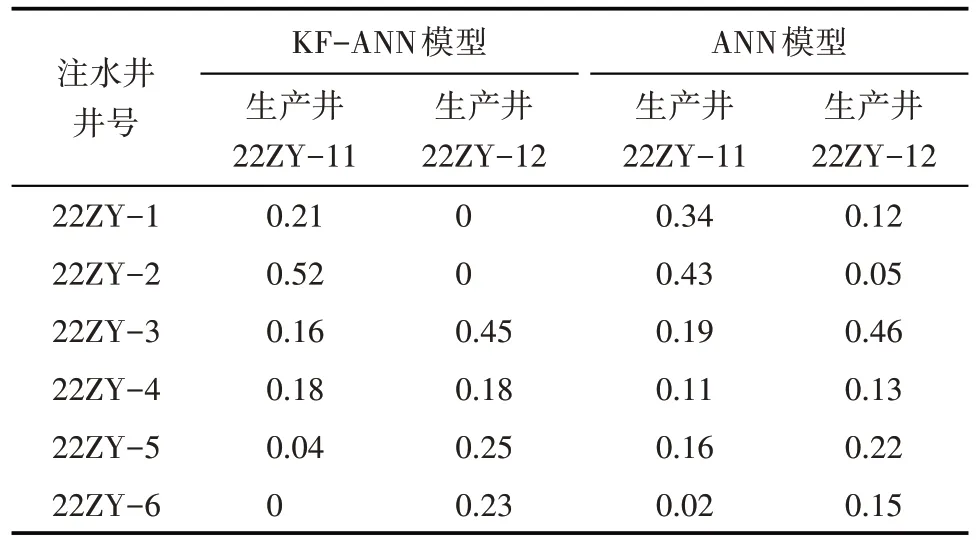
表5 KF-ANN与ANN模型的井间连通性分析结果对比Table5 Comparison results of interwell connectivity based on KF-ANN and ANN model

5 结论

基于注采井的动态生产数据，提出一种卡尔曼滤波和人工神经网络相结合的油藏井间连通性分析方法。应用卡尔曼滤波器和构建的非线性扩散滤波器分别消除注采数据的噪声污染、时滞特性和衰减特性对连通性分析的影响，通过构建的人工神经网络充分挖掘注采数据中蕴含的井间连通性关系。对均质、各向异性、包含封闭断层、具有高渗透带的4种典型特征油藏模型和实际非均质油田的应用结果表明，井间连通性计算结果与油藏地质特征高度吻合，验证了新方法的有效性和可靠性。对比基于卡尔曼滤波的ANN 模型与直接使用ANN 模型的井间连通性分析结果表明，数据降噪后的井间连通性分析结果更符合油藏地质特征，可有效识别注采井间的连通关系。建立的井间连通性分析方法可有效掌握注入水在地层中的流向，对指导开发方案的调整和认清剩余油分布具有重要意义。

符号解释

X(k|k-1)——利用k-1 时刻的预测结果；A，B——系统参数；X(k-1|k-1)——k-1 时刻的最优估计值；U(k)——k时刻的控制量；P(k|k-1)——X(k|k-1)对应的协方差；P(k-1|k-1)——X(k-1|k-1)对应的协方差；Q——系统噪声的协方差；X(k|k)——当前时刻的最优估计值；Kg(k)——卡尔曼增益；Z(k)——系统测量值；H——测量系统参数；R——测量噪声的协方差；P(k|k)——X(k|k)对应的协方差；αn——滤波系数；t——时间，月；n——离散的月份数，月；Δq——生产井产液量变化，m3/d；n0——离散月份数；——注水井i与生产井j之间的有效注入量，m3/d；——注水井i与生产井j之间的滤波系数；ii——注水井i的注入量，m3/d；xstd——归一化后的参数；x——待归一化的参数；R2——决定系数；l——样本索引号；L——数据点的个数，个；⁀ql——ANN 模型的预测产液量，m3/d；ql——实际产液量，m3/d；vara(β),varb(β),varc(β)——a,b,c3 组井间连通系数的方差；I——输入层向量；h——隐藏层向量；p——输出层向量；SEos——输出节点o对输入节点s的敏感性；po——第o个输出节点值；Is——第s个输入节点值；u——第u个隐藏层节点；po′——第o个输出节点的导数构成向量；wou——第o个输出节点与第u个隐藏层节点之间的权重；h′——第u个隐藏层节点的导数构成向量；vms——所有隐藏层节点与第s个输入节点之间的权重构成的向量；SEos,ave——注采井间连通性；SEos l——产液量与注水量数据集在第l 个数据样本的敏感性，该值越大，表示目标生产井与该注水井之间连通性越好。