海上S油田聚合物驱注采井网优化

屈亚光，阮 迪，未志杰，康晓东，严 巡

（1.长江大学石油工程学院，湖北武汉 430100；2.中海油研究总院有限责任公司海洋石油高效开发国家重点实验室，北京 100028）

目前，中国海上油田经过多年的开发大多已进入中高含水期，为了提高油田水驱开发效果，部分油田开展了聚合物驱矿场试验和实际开发部署，并取得了较好的增产效果［1-4］。随着聚合物驱开发的深入，特别是当油藏平面非均质性较强时，动用程度差异大，控水增油效果减弱，聚合物驱后剩余油分布复杂［5-10］。为后期调整阶段进一步改善聚合物驱开发效果，需不断调整井网，通过优化井距和井型，扩大波及效率［11-15］。为此，笔者基于海上S 油田的沉积相分布特征与井网部署的关系，建立合理的平面非均质物理模型，并且平板内置微电极用以监测含油饱和度分布，开展排状井网合理排距和不同注采井网形式的物理模拟实验研究，同时结合油藏数值模拟方法进一步研究不同平面渗透率级差与最优井排距之间的关系；并在充分认识合理井排距的基础上，采用物理模拟与油藏数值模拟相结合的方法，研究不同注采井网形式对聚合物驱开发效果的影响。

1 物理模拟实验

1.1 实验器材与方法

实验仪器 实验仪器主要包括：恒流泵、恒温箱、压力传感器、饱和度测试微电极、六通阀、手摇泵等。

实验流体 实验流体主要包括：①利用地层原油和标准0#柴油（密度为850 kg/m3，黏度为3.66 mPa·s）按一定比例配成模拟用油，65 ℃条件下原油黏度为60 mPa·s。②水驱和饱和模型用水均使用根据渤海油田注入水离子组成配制的复配水，矿化度为8 200 mg/L。③聚合物为渤海油田使用的聚合物，聚合物溶液质量浓度为1 350 mg/L。

实验条件 注入井采用恒流泵以恒定流量注入，采出井保持大气压定压生产；选取65 ℃作为实验温度。

方案设计 首先依据海上S 油田（渤海油田典型油藏）储层的沉积相分布特征，建立了包括高、中、低渗透3个区域的平面非均质物理模型，渗透率分别为1 500，1 000 和500 mD。渗透率条带与模型单元上、下边长的夹角均约呈22.5°，模型单元尺寸为40 cm×40 cm×5 cm，并在物理模型内部均匀布置了若干个饱和度测试微电极。由于海上S油田井网部署主要以正对排状注采井网为主，因此物理模型中设置的注采井网形式与海上S 油田保持一致，即采用排状注采井网。模型中共设置9口井（3口注入井，6 口生产井）。注入井井排与高渗透区域生产井井排距离为L1，注入井井排与低渗透区域生产井井排的距离为L2（图1），分别以L1与L2的比值为1.3，1.5，1.8，2.1和2.4，开展5组物理模拟实验。

图1 平面非均质物理模型示意Fig.1 Schematic diagram of plane heterogeneous physical model

实验步骤 实验步骤主要包括：①准备符合要求的平面非均质物理模型。②对模型抽真空饱和水，当模型完全饱和水后，记录累积吸水量。③启动恒流泵向模型注入油，直至饱和结束，记录累积排出水量，计算束缚水饱和度，然后老化48 h。④中间3 口注入井以恒定流量进行水驱，其中2 口边井注入速度为150 mL/h，中间1 口注入井的注入速度为300 mL/h，当模拟单元水驱含水率至80%时转聚合物驱，聚合物溶液总注入量为0.6 PV，直至后续水驱至含水率达到98%。⑤分别计量实验过程中的产液量、产油量、含水率、模拟时间和微电极饱和度等数据。⑥重复以上步骤，分别完成5 组物理模拟实验。

1.2 实验结果与分析

5 组物理模拟实验完成后可得到不同井排距比条件下典型油藏的累积产油量、累积注入量及模拟时间（表1）。统计不同井排距比的实验可知，当L1与L2之比不同时，实验结果（表1）差异较大。

表1 典型油藏平面非均质物理模型不同井排距比实验结果Table1 Experimental results of different well spacing ratio of plane heterogeneous physical model in the typical oil reservoirs

当井排距比为1.3 时，累积产油量为1 015.85 mL。在聚合物溶液总注入量相同的条件下，随着井排距比的增大，累积产油量起初也随之增加，其原因为低渗透区域储层的渗透率相对较低，聚合物驱替时相比高渗透区域储层受到的渗流阻力更大，生产井在同样的井底流压时，更易于向高渗透区域储层方向流动。随着井排距比的增大，注入井井排与低渗透区域生产井井排间的井排距减小，因此，低渗透区域储层动用程度增大。当井排距比增大到1.8 时，累积产油量为1 139.94 mL。随着井排距比的不断增大，累积产油量不增加反而降低，井排距比增大至2.1，累积产油量为1 079.15 mL。分析其原因为，当井排距比增大后，注入井井排与高渗透区域生产井井排的距离越来越大，两者之间的压力梯度随之减小；而注入井井排与低渗透区域生产井井排的距离减小后，两者之间的压力梯度变大，从而使得聚合物溶液在驱替过程中更易向低渗透区域方向流动，导致聚合物溶液注入后主要波及的是低渗透区域储层，使得高渗透区域储层动用程度变差。根据不同井排距采出程度与含水率变化关系，得出在不同井排距条件下，聚合物驱后注采单元的含水率下降幅度和含水率上升速度不同，如当井排距比为1.3 和2.4 时，聚合物驱后油藏模型整体的综合含水率降低幅度较小，主要是物理模型中受聚合物驱波及的范围较小，模型的综合含水率上升速度快，最终导致模型的采出程度低，聚合物驱开发效果差。在井排距比为1.8 时，物理模型的采出程度最高（表1）。

当物理模拟单元综合含水率达到98%时，根据部署在模型中32个含油饱和度微电极测试结果，分析物理模型中的含油饱和度分布状况，从而研究不同井排距比下的各类储层中的动用程度和波及效率。通过分析得出，当井排距比为1.3 和1.8 时的所有电极平均含油饱和度分别为29.27%和27.15%，对应的含水饱和度分别为70.73%和72.85%，井排距比为1.3 时的剩余油饱和度相对较高。由此表明，井排距比为1.8 时物理模型中各类储层的整体动用程度要高于井排距比为1.3。

为进一步分析模型中不同位置的含油饱和度分布状况，需对所有饱和度测试微电极的结果进行分析。通过统计分析可知，在不同的井排距比物理模拟方案中，平面非均质物理模型中部位置所布置微电极含油饱和度测试结果差别较小，靠近边部生产井的16 个微电极含油饱和度测试结果差异较明显，以模拟方案中井排距比为1.3 和1.8 为例进行详细的阐述（图2）。当井排距比从1.3 增加到1.8 后，对比不同渗透率储层内的含油饱和度可以看出，低渗透区域储层中8 个电极的平均含油饱和度从33.83%降低到29.27%，表明当注入井井排与低渗透区域储层生产井井排距离减小后，压力梯度增加，驱替动力增大，聚合物溶液平面上向低渗透区域储层流动的方向性提高，低渗透区域储层的动用程度大幅提高，驱油效率增加。而对于高渗透区域储层来说，由于注入井井排与生产井井排距离增加后，压力梯度减小，高渗透区域储层的8 个电极的平均含油饱和度从29.71%增加到31.11%，表明高渗透区域储层的波及效率略有降低。但从模型整体的动用程度来看，由于高渗透区域储层降低的幅度要小于低渗透区域增加的，因此，井排距调整后模型整体动用程度增加，2 个储层均得到有效动用，达到最佳均衡驱替状态。

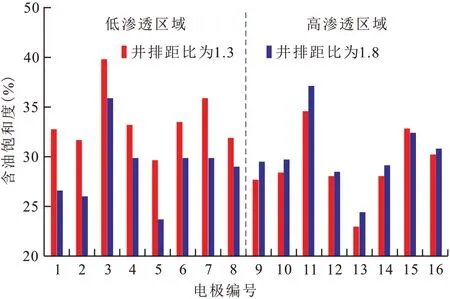
图2 不同井排距比下各电极的含油饱和度Fig.2 Oil saturation of each electrode with different well spacing ratio

2 油藏数值模拟

通过以上不同井排距比下物理模拟实验可以看出，对于平面非均质性较强，在井排与渗透率条带呈一定角度的储层，井排距比对聚合物驱的开发效果有较大影响，存在一个合理的范围。因此，有必要进一步针对海上S油田各个注采单元的平面非均质程度存在差异而研究不同非均质条件下的合理井排距比。

在室内物理模拟实验的基础上，采用油藏数值模拟方法先建立不同平面非均质条件的注采单元地质模型。然后再建立相应的油藏数值模拟模型，模型大小为300 m×300 m，厚度为6 m。数值模拟模型的平面渗透率分布特征与物理模型保持一致，设置高、中、低3 种不同渗透率的区域，井排方向与渗透率条带的角度也与物理模型相同（图1）。油藏数值模拟模型中渗透率区域设计了5种渗透率组合方案：方案1 的低、中、高渗透率分别为800，1 000 和1 200 mD；方案2 的低、中、高渗透率分别为666，1 000 和1 334 mD；方案3 的低、中、高渗透率分别为571，1 000 和1 429 mD；方案4 的低、中、高渗透率分别为500，1 000和1 500 mD；方案5的低、中、高渗透率分别为400，1 000 和1 600 mD。5 个方案的渗透率级差分别为1.5，2.0，2.5，3.0 和4.0。基于每个渗透率模型，采用排状注采井网，井排距比设计了8个方案，分别为1，1.27，1.5，1.78，2.13，2.57，3.17 和4。模拟计算的工作制度设定为注水井定注入量、生产井定井底流压。模拟过程首先水驱至含水率为80%，然后转注聚合物驱，连续注入聚合物为0.6 PV，后续水驱至含水率达到98%。通过油藏数值模拟方法可以计算得到各个方案的动态指标，方案优选指标用累积产油量和泰尔指数，其中泰尔指数是用来表征化学驱均衡程度的参数，当平面渗透率级差为3 时，按照不同的渗透率区域划分油藏单元并计算其泰尔指数。

泰尔指数方程为：

从图3可以看出，随着井排距比的增大，各方案的累积产油量先增加后降低，泰尔指数先降低后增加。当井排距比为1.78 时，累积产油量为102.7×104m3，达到最高，表明开发效果最优；泰尔指数仅为0.203 5，在所有模拟方案中最小，表明聚合物驱的均衡程度最高。

图3 平面渗透率级差为3时的泰尔指数和累积产油量Fig.3 Theil index and cumulative oil production when permeability ratio equals to 3

图4 平面渗透率级差为3时的不同井排距比的含油饱和度分布（综合含水率为98%）Fig.4 Oil saturation distribution of different well spacing ratio when permeability ratio equals to 3（comprehensive water cut is 98%）

同时，通过数值模拟计算可以得到模拟单元综合含水率达到98%时不同井排距比的含油饱和度分布（图4）。由于模拟单元和模拟工作制度完全一样，而且是模拟计算到综合含水率为98%时的状态，因此，各个方案含油饱和度分布的差异较小，需仔细观察。通过深入分析可以看出，当井排距比为1.27 时，模型中上半部低渗透区域储层剩余油富集区范围相对较大；而当井排距比为4时，不仅在低渗透区域存在剩余油富集区，在高渗透区域同样也存在剩余油富集区。而当井排距比为1.78 时，低渗透区域的含油饱和度富集区比1.27 时小、比井排距比为2.57 和4 时略大，但是高渗透区域含油饱和度富集区比井排距为2.57 和4 时均要小；结合上述对不同井排距比下的累积产油量分析，可得出井排距比为1.78 时低渗透区域储层采出程度的增加大于高渗透区域储层的降低，注采单元整体的采出程度高。通过油藏数值模拟方法得到的剩余油分布特征与室内物理模拟平面渗透率级差为3 时，物理模拟实验得到的最优井排距比为1.8 的微电极含油饱和度的测试结果是一致的。

不同渗透率区域储层的动用程度主要与注采井井排间的压力梯度有关，平面上聚合物溶液更易于向压力梯度大的方向流动。因此，通过调整注采井的井排距比，可以使得低渗透区域和高渗透区域2 个方向上的压力梯度基本一致，从而聚合物溶液平面上波及范围越大，注采单元的动用程度越高。

同理，对平面渗透率级差为1.5，2.0，2.5 和4 的地质模型，分别设计了8个井排距比模拟对比方案，通过油藏数值模拟计算可得到各个渗透率级差条件下最优井排距比，从图5可以看出，当平面渗透率级差为1.5 时，最优的井排距比为1.27；渗透率级差为2 时，最优的井排距比为1.5；当渗透率级差为2.5～4.0 时，得到了最优井排距比均为1.78。可知随着平面渗透率级差增大，最优井排距比也逐渐变大，注入井井排与高渗透区域的距离变大、注入井井排与低渗透区域的距离变小，使得2 个方向上的压力梯度趋于一致，高渗透区域和低渗透区域储层整体动用程度达到最优水平。

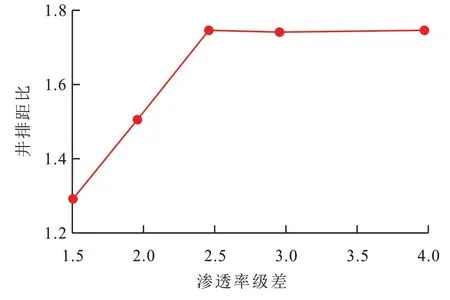
图5 不同渗透率级差条件下的最优井排距比Fig.5 Optimal well spacing ratio under different permeability ratio

3 注采井网形式对聚合物驱开发效果的影响

目前，海上S 油田主要以直井排状注采井网为主，因水平井在海上常规水驱油田开发中增油效果较好，因此，有必要研究水平井在聚合物驱油藏后期挖潜过程中的可行性及最优的注采井网组合形式。在图1 物理模拟基础上设计了3 组对比实验方案（图6），方案1 为排状注采井网（3 注6 采），方案2为水平井注直井采（1 注6 采），方案3 为水平井注水平井采（1 注2 采）。其中井排距比依据上面的优化结果，设定为1.78。

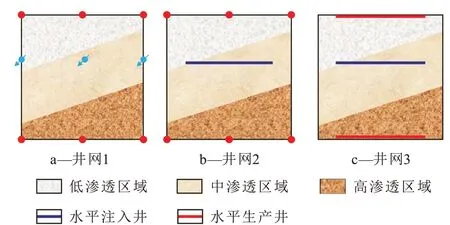
图6 3组对比实验方案Fig.6 Three groups of comparative experimental schemes

3 组对比实验方案的实验条件完全相同，每组方案单元总的注入速度为600 mL/h，生产井均是保持大气压定压生产，聚合物溶液总注入体积均为0.6 PV。3组实验的具体操作步骤和要求与1.2中一致。

根据3 种井网形式的模拟计算指标，按照不同的渗透率区域划分油藏单元并计算其泰尔指数（图7）可以看出，井网2 和井网3 的累积产油量较高、泰尔指数较低，表明水平井注直井采与水平井注水平井采驱替的均衡程度相对较高，开发效果优。主要原因是水平井注聚合物驱相对直井来说，井筒与油层接触面积更大，特别是当储层非均质性较强时，聚合物溶液向前推进的前缘更加均衡，平面非均质物理模型的波及效率更高。同时通过油藏数值模拟方法对3 组方案进行对比分析，得到的认识与采用物理模拟方法结果保持一致，采用水平井注水平井采是相对更优的调整方案。

图7 不同注采井网下的泰尔指数和累积产油量Fig.7 Theil index and cumulative oil production under different injection-production patterns

4 结论

依据海上S油田沉积相分布特征与实际井网部署关系，建立了多个平面非均质模型，基于排状注采井网分别采用物理模拟和油藏数值模拟方法，以累积产油量、饱和度微电极测试含油饱和度和泰尔指数为评价指标，通过对驱替压力梯度的深入分析，得出了最优的井排距比和最优的注采井网形式。通过研究分析表明，海上S 油田后期通过注采井排距比和注采井网形式的优化调整还能进一步提高油田聚合物驱的开发效果，为同类其他油田提供相关的技术指导。

符号解释

T——泰尔指数，即化学驱均衡程度指数，其值为0～1，泰尔指数越小，化学驱均衡程度越高；n——油藏中划分单元的个数，划分单元的个数越多，泰尔指数计算越准确；i——任意划分单元；Ri——第i个受效单元采出程度，%；R¯——所有划分单元采出程度的平均值，%。