评过剩吸附量和绝对吸附量关系式的不正确性

陈元千，傅礼兵，徐佳倩

（中国石油勘探开发研究院，北京 100083）

页岩吸附气和煤层吸附气都是重要的非常规天然气资源。该类资源的评价依赖于在不同压力下等温累积吸附量的计算和等温饱和吸附量的确定。不同压力下的等温累积吸附量，需要通过吸附仪的测试资料，利用有关的计算方法求得。文献［1-4］的研究结果表明，关于固相对气相的吸附问题，只有等温吸附量、等温累积吸附量和等温饱和吸附量，以及描述吸附方程和计算吸附量的方法，根本不存在所谓的过剩吸附量和绝对吸附量。两者之间的关系式也是不正确的。笔者将通过对文献［5-17］提出的所谓过剩吸附量和绝对吸附量关系的评论，让读者直接地了解所谓的过剩吸附量和绝对吸附量关系式的由来及存在的问题，并进行了有关的对比性推导和质疑性评论。

1 过剩吸附量和绝对吸附量关系式的由来及存在的问题

1.1 Adamson吸附关系式的不确定性

Adamson 于1976 年发表了名为《表面物理化学》的专著［5］，其中的第14 章为气体和蒸汽在固体上的吸附，在未给出任何理论推导的情况下，对于多层吸附，作者将固相吸附气相的质量表示为：

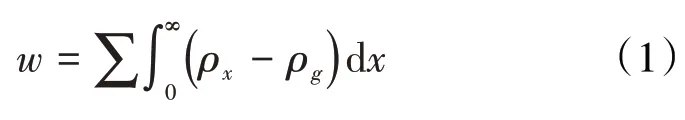
应当指出，作者除对w说明是固相吸附气相的质量外，其余包括参数和数学符号均未给予注释。这正是Adamson 吸附关系式不确定性的所在。当然，笔者也不便于作出任何解释。

1.2 Donohue和Aranovich吸附关系式的不正确性

Donohue 和Aranovich 于1998 年 基 于Adamson的吸附关系式，直接将所谓的多层过剩吸附量［6］表示为：

式中：Γexc为过剩吸附量，g；am为单层吸附能力，但从（2）式分析应当为固相体积，cm3；ρ为距固体表面y距离的固相密度，g/cm3；y为吸附方向距离，cm；ρb为固相本体（bulk）的密度，g/cm3。

对于单层吸附（monolayer adsorption），Donohue和Aranovich由（2）式得到：

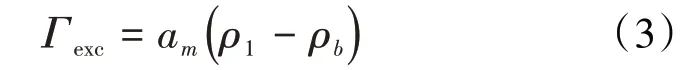
式中：ρ1为单层固相吸附气相后的密度，g/cm3。

由（3）式看出，am ρ1为固相吸附气相后的质量，am ρb为固相吸附气相前的质量，两者的差值为固相吸附气相的质量。Donohue和Aranovich毫无理由将am与ρ1的乘积，即固相吸附气相后的质量称为绝对吸附量。这正是绝对吸附量一词的由来。由此可以得到Donohue 和Aranovich 所谓的过剩吸附量与绝对吸附量的关系式为：

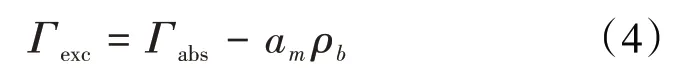
式中：Γabs为绝对吸附量，g。

让人不解的是，Donohue 和Aranovich 却突然将（3）式中固相吸附气相前的密度ρb错改为气相的密度ρg，得：

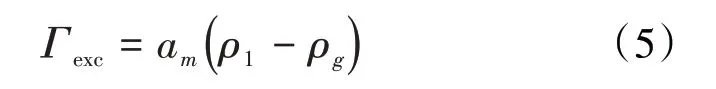
式中：ρg为气相的密度，g/cm3。

已知表示固相累积吸附气相的等温兰氏方程［1］为：

式中：Q为1 克岩样等温累积吸附气相的体积量，cm3/g；a和b为兰氏方程常数；p为吸附压力，MPa。

由文献［3］可知，气相密度与气相压力可近似用如下的直线关系表示：

式中：m为斜率。

Donohue和Aranovich提出，假定（5）式中的ρ1和ρg可分别用（6）式和（7）式表示，因此，将（6）式和（7）式代入到（5）式得：

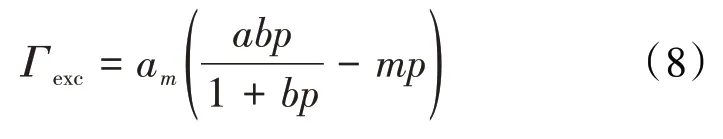
综上所述，由（3）式可以看出，固相吸附气相的质量是一个非常简单的关系式。但因Donohue 和Aranovich 将固相吸附气相的质量，称为所谓的过剩吸附量，又将am ρ1称为所谓的绝对吸附量，因此，为（4）式增添了既难以理解，又感到无奈的神秘色彩。实事求是地讲，Donohue和Aranovich提出的（3）式至（8）式，是一些什么问题都解决不了的虚式，它不能用于求得实际需要的等温累积吸附量和等温饱和吸附量，也没有任何理论价值。尤其将ρb错改为ρg得到的（5）式，导致了在中国热引的所谓过剩吸附量和绝对吸附量的关系式全是完全不正确的。

2 中国学者对Donohue 和Aranovich关系式的确认和引用

尽管Donohue 和Aranovich 提出的过剩吸附量和绝对吸附量及其关系式是不正确的，但仍被中国学者广泛的引用。首先是周理等于2000 年提出了与Donohue和Aranovich相同的如下关系式［7］：

式中：nexc为过剩吸附量，g；va为固相的体积，cm3；ρa为固相吸附气相之后的密度，g/cm3。

将（9）式改写为：

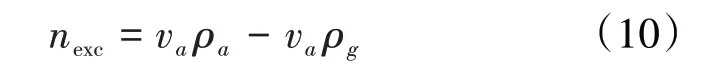
由（10）式看出，va ρa表示固相吸附气相后的质量，va ρg表示气相的质量，两者相减的数值是没有任何物理意义的。由于ρa≫ρg，va ρg的作用可以忽略不计。

周理等引用Donohue 和Aranovich 提出的概念，将va和ρa的乘积va ρa称为绝对吸附量。于是得到所谓的过剩吸附量与绝对吸附量的关系式为：

式中：nabs为绝对吸附量，g。

若将nabs=va ρa代入（11）式，得中国学者常用过剩吸附量和绝对吸附量的另一表达式为：

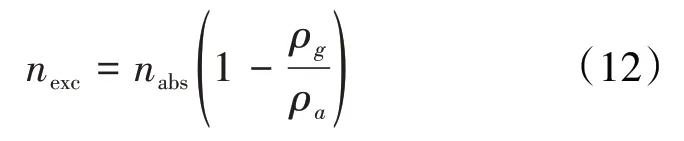
当用兰氏方程的（6）式描述绝对吸附量时，由（11）式可得中国有关学者用于计算过剩吸附量不正确的表达式为：

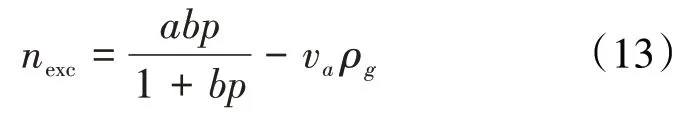
应当指出，在文献［10-13］中，作者将表示气体质量的va ρa理解为气体的浮力是不正确的。浮力应当是质量乘以重力加速度，即va ρag。

在2015 年至2018 年间，中国的有关学者对利用称量法如何计算等温累积吸附量的方法，发表了多篇有关过剩吸附量和绝对吸附量关系的文章［7-17］。现将这些关系式同Donohue 和Aranovich 的关系式以对比形式列于表1。由表1可以看出，不同作者在不同期刊上发表的关系式，只是符号不同，而内容完全相同。

3 对过剩吸附量和绝对吸附量关系式对比性推导和评论

在表1 中列出了近20 年来在中国广泛重视和引用的过剩吸附量和绝对吸附量的关系式。但应当指出，利用这些关系式，并不能求得等温吸附量、等温累积吸附量和等温饱和吸附量。为了拨乱反正，有必要进行如下的对比性推导和质疑性评论。

在文献［3-4］中，对于利用称重吸附仪测试的数据，确定mc克岩样累积吸附甲烷气的质量，可用如下质量平衡关系式表示为：

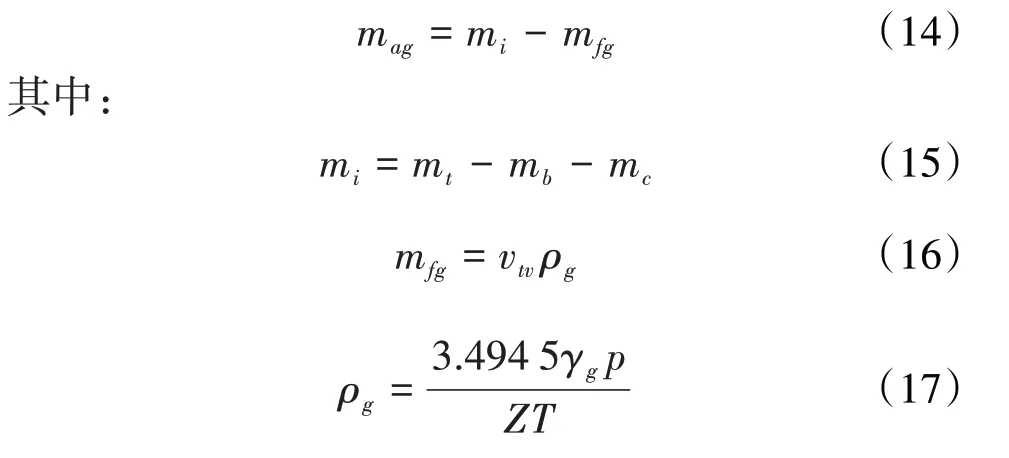
式中：mag为在某稳定压力p下mc克岩样累积吸附甲烷气的质量，g；mi为在某稳定压力p下向测试桶累积注入（injecting）甲烷气的质量，g；mfg为在某稳定压力p下测试桶的空余体积（void volume）内自由甲烷气的质量，g；mt为在某稳定压力p下称重法测试的总质量，g；mb为测试桶（barrel）的质量，g；mc为测试岩样（core sample）的质量，g；vtv为测试桶内的空余体积（void volume），cm3；ρg为空余体积内自由甲烷气的密度，g/cm3；γg为甲烷气的相对密度，dim；Z为空余体积内自由甲烷气的偏差因子，dim；T为气体的绝对温度，K。

将甲烷气的相对密度γg=0.553 8 代入（17）式得：

根据气体分子物理学，任何气体的质量除以其分子量，等于该气体的摩尔量。因此，将（14）式除以甲烷气的分子量，得mc克岩样累积吸附甲烷气的摩尔量为：

表1 不同作者发表的过剩吸附量与绝对吸附量关系式Table1 Relational expressions of excess adsorption capacity and absolute adsorption capacity published by different authors

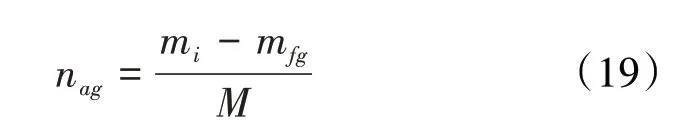
式中：nag为累积吸附甲烷气的摩尔量，mol；M为甲烷气的分子量，g/mol。

再由（19）式除以测试岩样的质量mc，可得1 克岩样累积吸附甲烷气的摩尔量为：

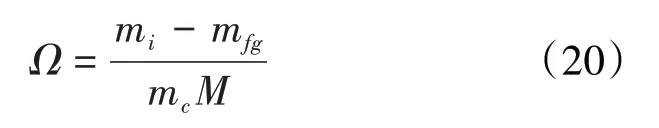
式中：Ω为1 克岩样累积吸附甲烷气的摩尔量，mol/g。

根据Avogadro（阿伏加德罗）定律［18］，1 摩尔的任何气体，在绝对温度为273.15 K 和绝对压力为1 atm（0.101 MPa）的条件下，占有的气体体积均为22 414 cm3。由于气体体积与温度成正比，因此，1摩尔的任何气体在293 K 和0.101 MPa 的地面标准条件下应占有的体积均为24 056 cm3。对此摩尔体积常数可称为Avogadro 常数，并表示为CA=24 056 cm3/mol。因此，1 克岩样累积吸附甲烷气的体积量为：

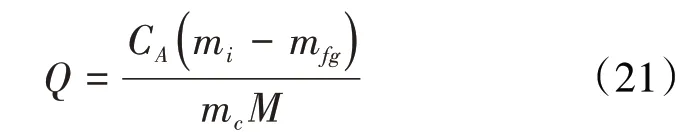
式中：Q为1 克岩样累积吸附甲烷气的体积量，cm3/g或m3/t。

将甲烷气分子量M=16.043 g/mol 和CA值代入（21）式，计算1克岩样累积吸附甲烷气的体积量为：

由以上对比性推导可以看出，利用称重测试仪测试的资料，通过（14）式可计算得到mc克岩样累积吸附甲烷气的质量。尽管表1中所列出的关系式与（14）式形式相同，但内涵是完全不同的。难道可以将mag和mi分别理解为过剩吸附量和绝对吸附量吗？这显然是不可以的。由本文的（14）式可以计算1 克岩样累积吸附甲烷气的质量、摩尔量和体积量，而表1 中所列的关系式只是一个虚构的而不可使用的关系式。试问，连什么是过剩吸附量和绝对吸附量的定义都没有，而且两者的含义都说不清楚，难道能得到正确的关系式吗？应用该关系式能求得需要的等温吸附量和等温累积吸附量，以及评价页岩和煤层吸附气资源量所需的等温饱和吸附量吗？答案是否定的。在参考文献［2-4］中已经提出了相应的计算方法。最后还想指出，Donohue 和Aranovich，以及表1中的不同作者，用兰氏方程表示ρ1值，以及用于计算绝对吸附量，是没有任何理论依据的，也只是想找一个解决问题的办法而已，但此办法事实上是行不通的。

4 结论

通过上述对比、分析和推证表明，Donohue 和Aranovich 于1998 年引用Adamson 不正确的固相吸附气相的质量平衡关系式，在没有任何物理定义的条件下，首次提出了过剩吸附量和绝对吸附量两个伪名词，以及两者之间的关系式。此关系式于2000年被周理等予以引用。其后，在2015 年至2018 年间，又被连续引用，先后在中国的一些重点期刊上发表了多篇文章，足见其影响之深刻。由对比性推证表明，固相吸附气相质量的关系式，根本不是什么所谓的过剩吸附量和绝对吸附量问题。过剩吸附量和绝对吸附量是作者人为提出的两个伪名词，两者之间的关系式是牵强附会不正确的。从固相对气相的吸附机理而言，只存在等温吸附量、等温累积吸附量和等温饱和吸附量，根本不存在所谓的过剩吸附量和绝对吸附量。请问提出和引用过剩吸附量和绝对吸附量关系式的作者，对此做何考虑？应当指出，某些学者利用兰氏方程表示绝对吸附量是没有任何依据的。表1 中所列的符号不同，而内容完全相同的过剩吸附量和绝对吸附量关系式是不正确的，也不能用于吸附理论的分析和实际上的应用。由Donohue 和Aranovich 提出并命名为过剩吸附量和绝对吸附量的关系式，是如此的简单，问题又是如此的突出。但经Donohue 和Aranovich冠以非常规的名称后，使得关系式增添了浓浓的神秘色彩，让人既怀疑又无奈。其实它说明不了什么问题，也解决不了什么问题。但却让一些学者如此入迷和追求，值得令人思考。