新型运动冗余驱动并联机构的控制方法

李善锋，杨 倩

（1.吉林铁道职业技术学院教务处，吉林吉林132200；2.绥化学院电气工程学院，黑龙江绥化152000）

在工业4.0快速发展的今天，串联机构已经不能满足生产的要求，人们已经将目光转移到了并联机构上［1-2］。并联机构由于其具备刚性好等特点在工业生产中得到了广泛应用［3］。并联机构在结构和性能上拥有其优越的特性，但其对预设轨迹进行准确追踪的问题，一直是困扰业界的一个难题［4-5］。

为了提高并联机构对预设轨迹的追踪准确性，人们研究出了多种控制方法。例如：Dion等［6］设计了关于速度与加速度的运动方程，确定最小可行振动次数的上限，以对并联结构的运动轨迹进行控制。文献［7］提出了一种基于积分滑模控制的双环控制方案，所提出的双环控制方案使用冗余传感器反馈，即使用适当的传感器获得单个主动关节位移、速度（在关节空间层）、末端执行器位置和方向（在任务空间层）作为反馈信号。利用冗余反馈信息，在外环（运动学）控制中计算末端执行器的实际位姿误差，在关节空间内环（动力学）控制中进行校正，以获得给定的任务空间轨迹。Jiang等［8］提出了一种6自由度悬索并联机器人的动态轨迹规划技术。首先，引入了一个与悬索并联机器人等效的被动机械系统，以提供洞察和帮助设计可扩展到机器人静态工作空间以外的轨迹。利用倾角和扭转角法则建立数学模型，并对轨道的旋转分量施加限制。在某些条件下，控制轨迹平动部分的动力学微分方程被证明是线性的。因此，得到了一个等刚度弹簧的等效无源线性系统的固有频率，并将与该系统相关的一组线性微分方程进行积分，得到了自然周期轨迹的一般解，用于跟踪纯平移轨迹和更复杂的运动。这些方法在控制并联结构时，不具备自适应性，难以适应并联机构的非线性影响，使得控制准确度不高。

对此，本文设计了一种3-RPR冗余驱动并联结构，并对其运动学进行了分析，获取了其结构中驱动机构和关节点的速度以及加速度方程；利用并联机构的同步误差，求取了滑膜面的计算方程，并在此基础上定义了自适应滑模控制器，求取了驱动力，以对并联机构的运动轨迹进行控制；最后，测试了本文设计的自适应滑模控制器对预设轨迹的追踪效果。

1 冗余驱动并联机构运动学分析

由于3-RPR非冗余驱动并联机构在运动时会受到奇点的影响，而且运动空间有限，所以在运动控制时效果不理想。对此，本文设计了如图1所示的3-RPR冗余驱动并联机构［9］。

图1 3-RPR冗余驱动并联机构结构图Fig 1 Structure diagram of 3-RPR redundant drive parallel mechanism

在图1中，3-RPR冗余驱动并联结构，动平台的中心点为I，圆形机构的中心为O。以I和O为中心，分别构建了I-x1y1z1和O-x2y2z2两个坐标。在I-x1y1z1中，z1与动平台垂直；在O-x2y2z2中，z2与圆形机构垂直。各支链由第1和第2移动机构构成，C1，C2，C3为关节点，D1，D2，D3为驱动机构，T1，T2，T3为与连杆相连接的3个关节的长度，φi(i=1，2，3)为I-x1y1z1下动平台的3个关节点和x1轴方向相成的夹角，γi(i=1，2，3)为O-x2y2z2下3个圆形机构连杆和z2轴方向相成的夹角，δi(i=1，2，3)为O-x2y2z2下3个连杆和z2轴方向相成的夹角。

在O-x2y2z2中，可利用旋转矩阵Rφi和半径矩阵，计算驱动机构的位置向量［10-11］：

动平台可被视为一个等边三角形，其边b=ICi由I点和C1，C2，C3组成。Ci（i=1，2，3）在I-x1y1z1和O-x2y2z2两个坐标下的位置向量分别为

式中：Ti（i=1，2，3）为关节的长度；si=DiCi为Di到Ci的单位矢量；uCi为Ci（i=1，2，3）在I-x1y1z1中的坐标。其可利用矩阵Rφ和Rφi及uˉCi来表示：

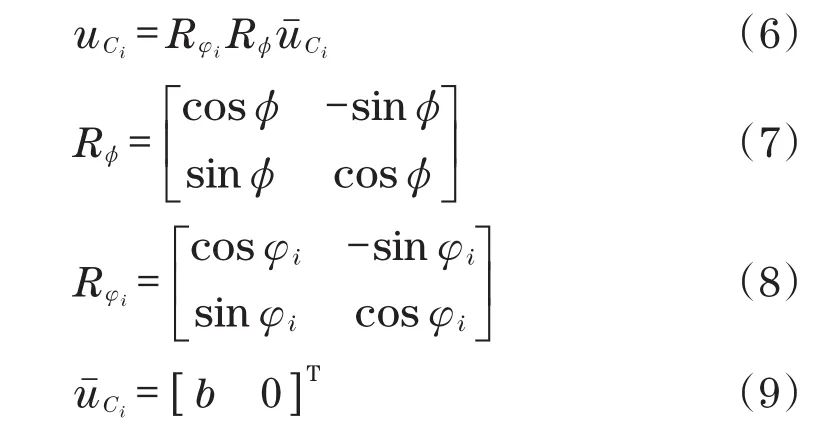
式中：φ为动平台的几何中心的方向。

通过联合式（4）和式（5），可获得Ti（i=1，2，3）的求取过程为

由式（1），可得驱动机构Di的速度计算式为

通过对式（5）求导，可得到关节点Ci的速度计算公式为

在O-x2y2z2坐标中，关节点Ci的速度计算公式为

式中：T˙i为第2移动机构的速度，其计算过程为

在获得驱动机构Di以及关节点Ci的速度后，对其进行求导，便可得到对应的加速度计算过程为

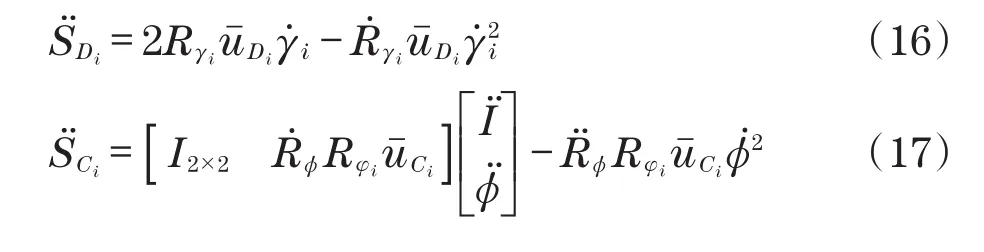
2 控制器设计

滑模控制方法将预设轨迹视为目标，控制并联机构按照预设轨迹运转［12］。滑模控制方法控制并联机构到达滑膜面后，将会具有较好的鲁棒性。对此，采用滑模控制方法设计了一种自适应滑模控制器。所设计的自适应滑模控制器可以对并联机构的运动学参数进行估计，同时协调其各支链间的驱动力，以对并联机构的运动轨迹进行准确的控制。

利用预设轨迹qe和实际轨迹qd的误差e，求取并联机构的同步误差［13］为

式中：J(θ)为一个关于预设轨迹切线处角度θ的矩阵，

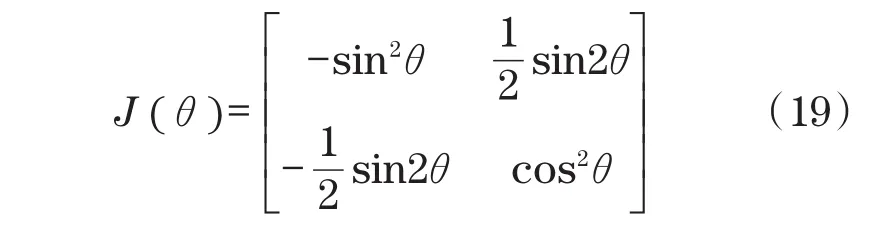
利用es可得到滑膜面的方程为

式中：a1和a2为正常数；为es的导数。

通过滑膜面的方程，求取参考速度与加速度的方程为

利用参考速度与加速度对自适应滑模控制器进行定义，求取驱动力uc为

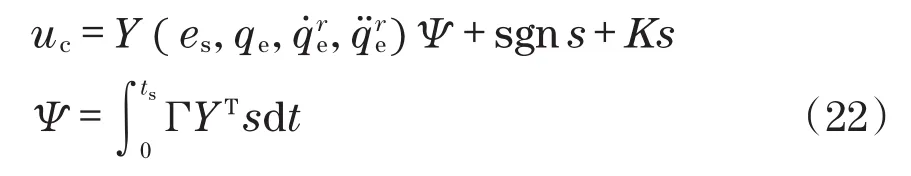
式中：K=diag(k1，k2)，k1，k2为正常数；Y(es，qe，)为一个矩阵；ts为采样时间。

3 实验结果

在Matlab/Simulink下进行实验。用本文设计的自适应滑模控制器（Adaptive Sliding Mode Controller，ASMC）对不同预设轨迹进行了追踪测试。同时实验中还将神经网络控制器（Neural Network Controller，NNC）与ASMC一同用于对预设轨迹的追踪测试，作为实验测试过程的对比，以比较本文设计的ASMC的控制优越性。

3.1 简单预设轨迹追踪

利用ASMC和NNC对利用直线变换产生的简单预设轨迹进行追踪，并对各控制器追踪的结果进行分析，判断各控制器的追踪特性。ASMC和NNC对简单预设轨迹的追踪结果如图2所示。

将图2（a）和图2（d）进行比较发现，ASMC和NNC都能实现对预设轨迹进行追踪。截取ASMC和NNC的部分追踪轨迹进行分析可以发现，如图2（b）和图2（e）所示，NNC和ASMC对简单预设轨迹追踪结果在x方向上的误差：NNC的追踪轨迹在x方向上出现的跳动频率，比ASMC的追踪轨迹在x方向上出现的跳动频率高；NNC的追踪轨迹在x方向上出现的最大误差为4.86 mm，而ASMC的追踪轨迹在x方向上出现的最大误差仅为2.52 mm。如在图2（c）和图2（f）所示，NNC和ASMC对简单预设轨迹追踪结果在y方向上的误差：NNC的追踪轨迹在y方向上波动的次数，比ASMC的追踪轨迹在y方向上波动的次数多；NNC的追踪轨迹在x方向上出现的最大误差为4.52 mm，而ASMC的追踪轨迹在x方向上出现的最大误差仅为2.49 mm。由此可见，本文设计的ASMC能够对简单预设轨迹进行较准确的追踪，说明ASMC可以控制3-RPR冗余驱动并联机构，较好地按照直线变化产生的较为简单的预设轨迹进行运动。

图2 NNC和ASMC对简单预设轨迹追踪结果Fig.2 Tracking results of simple preset trajectory by NNC and ASMC

3.2 复杂预设轨迹追踪

用ASMC和NNC对利用曲线产生的复杂预设轨迹进行追踪，通过分析追踪结果，观察各方法性能。ASMC和NNC对复杂预设轨迹的追踪结果如图3所示。

对比图3中NNC和ASMC对复杂预设轨迹追踪结果可见，图3（a）中的追踪轨迹比图3（d）中的追踪轨迹更具波动性。如图3（b）所示NNC的追踪轨迹在x方向上的误差，比图3（e）所示的ASMC的追踪轨迹在x方向上的误差更大，而且波动次数也更多。图3（b）中的最大误差为4.95 mm，图3（e）中的最大误差为3.53 mm。如图3（f）所示ASMC的追踪轨迹在y方向上的误差曲线，比图3（c）所示的NNC的追踪轨迹在y方向上的误差曲线更为平稳，波动次数更少。图3（f）中的最大误差为3.51 mm，图3（c）中的最大误差为4.93 mm。由此说明ASMC比NNC对复杂预设轨迹的追踪效果更好，能够较好地减少追踪过程产生的误差。表明ASMC可以对3-RPR冗余驱动并联机构的运动轨迹进行较为准确的控制，而且控制过程较为平稳。

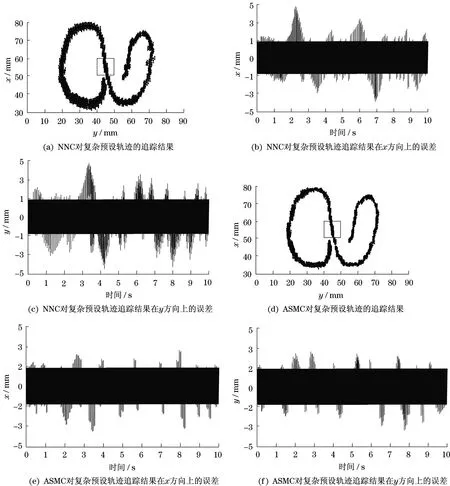
图3 NNC和ASMC对复杂预设轨迹追踪结果Fig.3 Tracking results of complex preset trajectory by NNC and ASMC

4 结语

本文通过具有移动副和转动副的3条支链设计了一种3-RPR冗余驱动并联结构。对该并联机构中的关节点和驱动机构的位置向量进行了计算，求取了其各自对应的速度方程。利用并联机构的同步误差，建立了滑膜面的计算方程，通过该方程求取了参考速度与加速度，进而构造了自适应滑模控制器。通过利用自适应滑模控制器对预设轨迹进行追踪的结果显示，自适应滑模控制器对简单和复杂预设轨迹的追踪效果都较好，说明自适应滑模控制器具有对3-RPR冗余驱动并联结构较好的控制特性。