粤西地区及各地级市新型冠状病毒肺炎疫情发展趋势预测分析—基于Holt 双参数指数平滑模型的研究

林挺葵，吴家园，刘华锋，潘振宇，李筱，赖维光，赖天文，吕军

2019 年12 月，湖北省武汉市发生了一起新型冠状病毒肺炎（coronavirus disease 2019，COVID-19），之后已迅速蔓延至其他地区。冠状病毒是一个大型病毒家族，可引发呼吸系统疾病、中东呼吸综合征（MERS）、重症急性呼吸综合征（SARS）等严重疾病［1-2］，但新型冠状病毒是既往从未在人体内发现的冠状病毒新毒株。截至2020 年2 月18 日24 时（文中数据均截止于此日期），国家卫生健康委员会官方网站显示，全国31 个省（市、自治区）累计报告COVID-19 确诊病例高达74 185 例，其中治愈14 376 例、死亡2 004 例［3］，而广东省累计报告COVID-19 确诊病例为1 331 例，其中治愈571 例、死亡5 例［4］。随着近期政府加强疫情防控，尤其是全国对口医疗支援力量的加强，疫情防控工作已取得积极成效，疫情形势出现积极变化。虽然目前我国COVID-19 治愈出院病例数高达1 万以上，且除湖北省以外新增确诊病例数出现13 d持续下降，但疫情防控仍处在关键时刻，尚存在诸多不确定风险和挑战。

粤西地区位于广东省西部，包括湛江、茂名、阳江3 个地级市，人们对疫情防控及发展趋势极为关注，如疫情“拐点”何时出现？何时能达到峰值？疫情是否能被控制？何时复工、复学?基于这些问题，笔者通过构建传染病动力学Susceptible-Infected-Recovered（SIR）模型以计算现阶段粤西地区及各地级市COVID-19 的基本再生数（R0），并采用Holt 双参数指数平滑模型预测疫情发展趋势，为疫情防控及相关政策的制定提供参考依据。

1 对象与方法

1.1 数据来源 2018 年底湛江市、茂名市和阳江市人口数分别为729 万、632 万和256 万（信息来源于上述地级市政府官网［5-7］），三地2018 年底人口数相加即粤西地区2018 年底的总人口数。本文相关数据来源于广东省卫健委截止2020 年2 月18 日24 时的官方网站［4］，粤西地区COVID-19 累计报告确诊病例49 例，其中阳江市13 例、茂名市14 例、湛江市22 例，暂无死亡病例，无医务人员感染。

1.2 SIR 模型的构建 SIR 模型又称“仓室”模型，是最经典的传染病模型。在SIR 模型中，发病区域内的人群被分为三类：（1）易感者（susceptible，S），指尚未感染但易受到感染的人群；（2）感染者（infected，I），指已感染并可以传染给他人的人群；（3）移出者（removal，R），指感染后治愈且对该传染病免疫，或已死亡的人群。这三类人群在易感状态、传播状态和移出状态间的转换不仅依赖于自身状态，同时也受周围人群所处状态的影响。SIR 模型的构建基于以下四个方面的基本假设：（1）该地区的总人口数保持恒定；（2）单位时间内，感染者所能传染的人数与易感者人数成正比；（3）单位时间内，移出者人数的增加和感染者人数成正比；（4）移出者在疫情期间不会再次感染［8］。根据上述假设，经典SIR 模型可用一组微分方程表示：

在上述公式中，S（t），I（t）和R（t）分别表示t 时刻易感人群、感染人群和移出人群的数量，在初始时刻三类人群数量均大于0；β表示感染强度，即感染者传播疾病的效率；γ 表示移出概率，即感染者治愈的概率。本研究使用R 语言（3.6.1 版本）deSolve 包构建SIR 模型，并估算R0。

急性传染病的R0 属于时间序列数据，按照不同特征可分为趋势性、季节性、平稳性和不规则性［9］，其中趋势性指时间序列可随着时间的变化存在整体向上或向下的趋势；季节性指时间序列在一定周期内出现波动，一般以1 年为1 个周期；平稳性指数据序列不会随时间变化而变化；不规则性指时间序列呈现一种无规律可循的变化。

1.3 Holt 双参数指数平滑模型的构建 指数平滑模型是估算时间序列数据趋势性的一种常用方法，主要通过对近期及远期数据进行差异性赋权来实现历史数据的加权修匀，从而提取序列的确定性信息，其突出的优点在于预测结果既可反映最新信息，也不会遗漏历史信息，有利于确保预测结果更加符合实际，且计算简单直观［10］，该模型主要用于中短期预测。指数平滑模型包括非季节性指数平滑法（包括简单性指数平滑法、Brown 单参数线性指数移动平均法、Holt 指数平滑法）和季节性指数平滑法（包括简单季节性指数平滑法、Winter 可加性指数平滑法、Winter 可乘性指数平滑法），考虑到COVID-19 疫情的历史数据并不具有季节性，故本研究采用Holt 双参数指数平滑法。Holt 指数平滑法是一种线性指数平滑方法，适用于具有线性趋势但无季节变化的时间序列，因具有较大的灵活性而被广泛使用。Holt 双参数指数平滑模型由一个预测公式和两个平滑公式组成，其中两个平滑公式分别反映线性平滑信息、趋势平滑（增量）信息，具体公式如下：

在上述公式中，k＞0，为预测超前期数； at表示t 时期的指数线性平滑预测值；yt为t 时期的实际观察值；bt表示利用前t 数据对当前时期t 趋势增量b 的估计值；y^t+k为利用前t 数据对低t+k 期的预测值；α和β为平滑参数，取值在0～1 之间［11］。选取最优的平滑参数α和β对保证Holt双参数指数平滑模型的预测效果十分关键。本研究通过SPSS 24.0 统计学软件计算预测值与真实值间的残差平方之和，即RSS(β，γ)=Σt〔I（t）-Î（t）〕2，并依据其最小值来确定模型的最优参数而选择最优模型。此外，本研究还采用Pearson 相关性分析计算相关系数γ，以评估Holt 双参数指数平滑模型的预测效果。

2 结果

2.1 R0 计算结果及分析 粤西地区及各地级市2020 年1 月25 日—2 月18 日COVID-19 R0 计算结果见表1、图1，采用Holt 双参数指数平滑法进行拟合和预测，参数设置和最优参数设置见表2。2020 年1 月25 日—2 月18 日COVID-19 R0的观察值与预测值相比较，粤西地区的最大相对误差为2.65%，其中湛江市为2.55%、茂名市为3.36%、阳江市为3.28%。另外，粤西地区COVID-19 R0 最大值为2.06，见于疫情初期，随后呈持续下降趋势，至2 月18 日到达本次观察期最低值（1.13）（见图2A）；湛江市、茂名市、阳江中COVID-19 R0 最大值均见于疫情初期，分别为1.54、2.36、1.59，其中湛江市和阳江市COVID-19 R0 呈波动下降趋势（见图2B 和2D），而茂名市COVID-19 R0 在疫情初期迅速下降后，表现为稳中有降趋势（见图2C）。

2.2 Holt 双参数指数平滑模型的预测效果 Pearson 相关性分析结果显示，Holt 双参数指数平滑模型对粤西地区及各地级市COVID-19 R0 的预测值与观察值的相关系数均接近1（P＜0.01，见表3），可见Holt 双参数指数平滑模型对粤西地区及各地级市COVID-19 R0 的预测较准确。

2.3 Holt 双参数指数平滑模型对粤西地区及各地级市COVID-19 R0 的预测结果及分析 采用Holt 双参数指数平滑模型对粤西地区及各地级市COVID-19 R0 未来趋势的拟合和预测结果见图2，可见约在2 月底，粤西地区及各地级市COVID-19 R0 将回落至低于1 的水平，预示COVID-19 疫情可能迎来“拐点”，该疫情可能已被控制并走向消亡。各地级市可能迎来“拐点”的时间相差不大，可见各地级市目前所采取的防控措施是积极有效的。

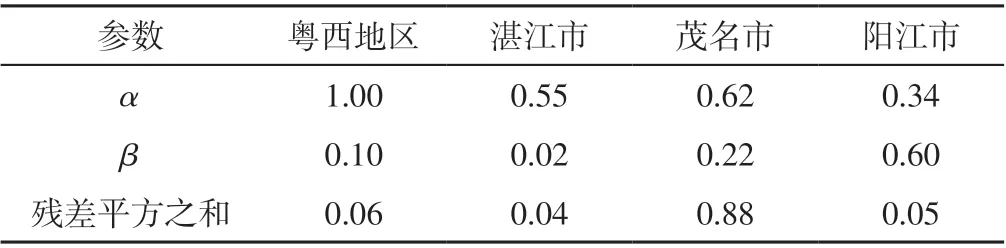
表2 粤西地区及各地级市COVID-19 疫情Holt 双参数指数平滑模型参数Table 2 Parameters of Holt two-parameter exponential smoothing model for the epidemic of COVID-19 in Western Guangdong and other prefecturelevel cities

表3 粤西地区及各地级市COVID-19 R0 的观察值与预测值之间的相关性Table 3 Correlation between observed and predicted value of R0 in predicting the epidemic trend of COVID-19 in Western Guangdong and other prefecture-level cities

3 讨论

2020 年1 月19 日，国家卫生健康委确定了广东省首例输入性COVID-19 确诊病例，仅4 d 后，广东省人民政府结合当前COVID-19 疫情防控形势，决定启动重大突发公共卫生事件一级响应，各地级市严格落实国家、省防控工作部署及广东省重大突发公共卫生事件一级响应要求，动员社会各方力量，采取有力、有效的措施全力防止疫情蔓延，维护好人民群众的生命安全和身体健康。针对春节后返工潮的到来，粤西各地级市按照“轻重缓急，分类指导、分期分批”的原则引导务工人员安全有序返岗。同时，采取“外防输入”“内防扩散”的防控措施有效遏制疫情蔓延势头，并取得了明显的阶段性成效。R0 值反映传染病暴发的潜力和严重程度，R0 值越高表明疫情越严重，而R0 值主要取决于疾病的传染率、人与人的接触率及传播时间［12］。本研究针对粤西地区COVID-19 疫情构建SIR 模型来计算现阶段粤西地区及各地级市COVID-19 的R0，结果显示，粤西地区疫情初期COVID-19 R0 最大值为2.06，低于武汉市同期COVID-19 的R0（2.8～3.9）［13］，其中湛江市、茂名市和阳江市的R0 最大值分别为1.54、2.36、1.59。从对疫情的认知来看，新型冠状病毒主要通过呼吸道传播，是可防可控的。积极治疗和严格隔离感染者，切断传播途径，增强民众对疫情的认识及加强防护措施均能降低R0 值，进而有效控制COVID-19 疫情。

图1 粤西地区及各地级市2020 年1 月25 日—2 月18 日COVID-19 R0 变化趋势Figure 1 Variation trend of R0 of COVID-19 in Western Guangdong and other prefecture-level cities from January 25 to February 18，2020

表1 粤西地区及各地级市2020 年1 月25 日—2 月18 日COVID-19 R0 计算结果Table 1 Calculated R0 of COVID-19 in Western Guangdong and other prefecture-level cities from January 25 to February 18，2020

本研究采用Holt 双参数指数平滑模型对现阶段COVID-19 流行趋势进行了估计和预测，结果显示，粤西地区及各地级市COVID-19 R0 的预测值与观测值的相关系数均接近1，表明Holt 双参数指数平滑模型对COVID-19 R0 的预测较准确，且根据预测模型结果，在现有高效防控措施下，粤西地区及各地级市的COVID-19 疫情逐渐好转，可能在2 月底迎来“拐点”，这与该地区政府采取了快速有效的疫情防控措施、民众防范意识的提升及医疗卫生事业发展密切相关。

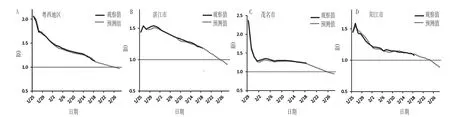
图2 粤西地区及各地级市COVID-19 R0 变化趋势及预测Figure 2 Variation trend and forecasting for R0 of COVID-19 in Western Guangdong and other prefecture-level cities

突如其来的COVID-19疫情对我国经济的影响备受关注。广东省作为中国经济第一大省，已于2020 年2 月10 日起陆续进入有序复工复产阶段，医疗物资、能源、粮食、交通物流等重点领域企业均已陆续开工。复工复产有利于为疫情防控提供充足的物资保障，进而减少疫情对经济的影响。目前，疫情防控仍处于关键阶段，因此，企业单位应制定应急处理方案、严格落实医学观察措施、设置隔离观察场所、加强复工人员的健康管理、保障员工的心理健康。此外，受疫情的影响，学校延迟开学，一些考试推迟或暂停，而何时复学是人们最为关注的问题之一。根据预测模型结果，为防止二次暴发，复学时间应在实际疫情走向消亡的基础上加上14 d 的医学观察期。因此笔者建议复学时间应晚于2 月底。此外，笔者还建议学校要错峰、错层次、错区域开学；学校要掌握校园风险隐患；加强宿舍、食堂及教室等区域的消毒工作；校内实行网格化管理；做好疫情防控物资储备工作并设置隔离观察场所；对进出校园的人员进行严格监管；强化心理疏导，保障师生的心理健康。

综上所述，Holt 双参数指数平滑模型对粤西地区及各地级市COVID-19 疫情发展趋势的预测较准确，并预测在现有的高效防控措施下，粤西地区及各地级市的COVID-19 疫情正在好转，有望在2 月底迎来“拐点”。继续保持目前的防控措施不松懈，是扑灭疫情的关键所在；但本研究存在一定局限性：首先，本研究数据于公开数据，仅考虑了已确诊和有症状的感染者，未涵盖无症状感染者，目前已发现无症状感染者也可传播疾病，可能会导致R0 的估算结果不能真实反映疫情实际情况；其次，本研究的假设相对理想，可能会对预测结果造成一定影响。

作者贡献：吴家园、刘华锋、吕军进行文章的构思与设计；林挺葵、李筱、赖天文进行研究的实施与可行性分析；林挺葵、潘振宇、李筱、赖维光进行数据收集、整理、分析；吴家园、赖天文、吕军进行结果分析与解释；林挺葵、吴家园、赖天文负责撰写论文；刘华锋、潘振宇、吕军进行论文的修订；吴家园、刘华锋、吕军负责文章的质量控制及审校；赖天文、吕军对文章整体负责，监督管理。

本文无利益冲突。