非饱和全空间埋置隧道动力响应半解析模型

2020-04-12狄宏规郭慧吉王炳龙张小会

同济大学学报（自然科学版） 2020年3期

狄宏规，郭慧吉，王炳龙，张小会

（1. 同济大学道路与交通工程教育部重点实验室，上海201804；2. 同济大学上海市轨道交通结构耐久与系统安全重点实验室，上海201804）

近年来，大量轨道交通隧道的投入运营产生了许多因行车振动而导致的环境振动和结构病害问题，尤其在软土地层中，由于土层容易变形，因此病害问题更为突出［1-3］。隧道系统车致振动及其引起的结构病害和环境振动问题的解决，关键在于建立可靠的隧道系统耦合动力学分析模型，通过动力学方法从理论上进行解释，以便采取有效的工程技术措施。

现阶段隧道动力响应计算模型主要包括两大类，即解析（半解析）模型与数值法模型。常见的解析（半解析）模型有欧拉梁模型［4］、Pip in PiP（PiP）模型［5-9］、时域动力子结构模型［10］以及面波转化法模型等［11-12］。解析（半解析）模型计算速度快、参数分析方便，可以更深层次地了解振动传播的一般规律。与解析法、半解析法相比，数值法的优势在于可以进行更为精细化的建模。常见的数值法模型包括有限元模型［13-14］、2.5维有限元模型［15］、周期性有限元-边界元模型［16］、2.5 维有限元-边界元模型等［17-19］。上述模型均将土体视为单相线弹性介质或固、液两相介质，而天然土体通常由固相、液相、气相等介质组成，因此采用单相或两相介质难以真实模拟地基土的多相特性。为了考虑气相对土体动力响应特性的影响，国内外学者基于等效流体原理、混合物理论等，先后推导了非饱和多孔介质波动控制方程［20-22］。随后，徐明江等［23］、Fang等［24］、郭鹏飞等［25］建立了非饱和地基上路基、桩基动力响应分析模型。然而，对于非饱和地基中隧道动力响应分析模型的研究较为鲜见。

将隧道外的非饱和地基土视为固、液、气三相介质，隧道视为无限长的Flügge薄壁圆柱壳，分别采用矢量分解定理以及分离变量法求解非饱和地基土的波动方程和Flügge薄壁圆柱壳的振动控制方程。然后，利用隧道与土体交界面处的边界条件，在频域-波数域内进行耦合求解，得到系统的动力响应基本解。最后，利用傅里叶逆变换得到时域-空间域内的响应。

1 非饱和地基土-隧道耦合模型以及求解

1.1 模型的简化

地基土与隧道衬砌分别采用中空圆土柱以及无限长的Flügge薄壁圆柱壳模拟。地基土由固、液、气三相介质组成。壳体由均质、各向同性的线弹性材料组成，如图1所示。模型边界假定为：非饱和土体与衬砌接触面处位移、应力连续，并且隧道衬砌不透水、不透气；非饱和土柱外径无穷大，无限远处土体的应力、位移衰减为零。

图1 非饱和地基土-隧道系统简化模型Fig.1 Simplified model of unsaturated soil-tunnel system

图1中，r、z、θ分别为圆柱坐标系下径向、轴向以及角度的物理量分量，us、v、w、uq分别为土骨架位移、孔隙水相对于土骨架的位移、气体相对于土骨架的位移以及壳体位移，q为壳体应力，R1为隧道半径，h为衬砌厚度，P为激振荷载，v0为荷载移动速度。

1.2 非饱和地基土波动方程及求解

文献［23］中运用连续介质力学理论，结合空间平均化方法，基于Mualem 理论考虑孔隙流体相对于固体骨架的渗透系数，并采用非饱和地基土的水土特征曲线Van Genunchten（V-G）模型，推导了非饱和地基土的实用波动方程，如下所示：

式中：u 为位移矢量；p 为压力；ρ 为密度；λ、μ 为土骨架Lame 常数；γ 为有效应力系数；下标s、l、g 分别表示土颗粒、孔隙水以及气体。式（1）中的其他变量表达式如下所示：

式中：K为压缩模量；n0为土体孔隙率；Sr、Sw0分别为饱和度与约束饱和度；η为黏滞系数；krl、krg分别为孔隙水和气体的渗透系数；κ为渗透率；m为V-G模型的拟合参数。

渗流连续性方程为

a11、a12、a13、a21、a22、a23表达式参考文献［23］。

引入非饱和多孔介质的平均密度ρ、孔隙水与固体骨架间的相对位移v以及气体与固体骨架间的相对位移w，计算式如下所示：

将式（1）写成us-v-w的表达形式，如下所示：

其中，

渗流连续性方程可改写为

总应力表达式为

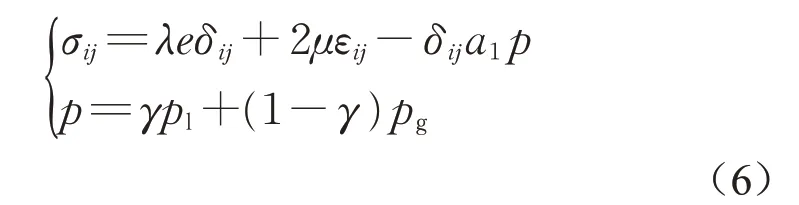
式中：σij为土单元总应力分量；e为体积应变；εij为应变分量；δij为克罗内克符号；p为等效孔隙流体压力。

根据Helmholtz 矢量分解定理，式（4）中各位移us、v、w分别表示为

式中：φ、ψ 分别为土骨架部分的标量波函数和矢量波函数；φ、τ分别为孔隙水部分的标量波函数和矢量波函数；χ、ϖ 分别为气体部分的标量波函数和矢量波函数；ez为z方向的单位向量。

考虑稳态响应，将式（7）代入式（4），对时间t 进行傅里叶变换至频域后，得到以下方程组：

式中：ω为角频率；～表示时间t所对应的频域。

为保证微分方程组（8）有非零解，则需满足系数矩阵行列式为零的条件。根据该条件可以得到以下Helmholtz方程：

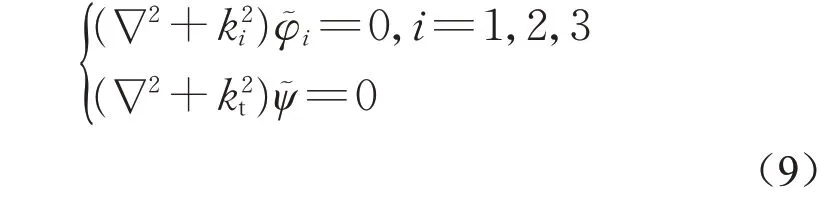
式中：k1、k2、k3分别为非饱和地基土中的快纵波、慢纵波、第二类慢纵波波数；kt为非饱和地基土中的横波波数。

利用式（8）、（9），经推导整理，可以得到各相势函数之间的关系系数ς1l、ς2l、ς3l、ς1g、ς2g、ς3g、ςtl、ςtg，各相势函数之间的关系可表达为

为满足式（9）的解，假定势函数具有以下形式［8］：式中：n为环向模态分量；ξ 为z方向波数；

将式（11）代入式（5）～（7）中，并对z方向进行傅里叶变化，得到单个环向模态分量n下位移、应力以及孔压在频率-波数域内的分量，如下所示：

其中，

1.3 隧道衬砌振动控制方程及求解

隧道衬砌采用Flügge 薄壁圆柱壳模拟，壳体振动控制方程及求解可参考文献［5］，壳体的平衡方程可写成以下矩阵形式：

式中：υ 为壳体泊松比；E 为壳体杨氏模量。H 中元素的表达可参考文献［5］。

1.4 耦合求解

假设衬砌内表面z=0 m、θ=0°处作用一个沿z向正方向以v0速度移动的单位简谐点荷载（见图1），则单个环向模态分量n 下频率-波数域内荷载在r、θ、z方向产生的应力分量分别为

式中：δ为狄拉克函数；ω0为激振荷载的角频率。

结合土体与衬砌接触面处位移、应力连续，同时隧道与土体界面的孔隙水、气体压力变化均为零，即，得到以下计算式：

式中：G0由G对r求导所得。

由式（15）求解出未知量B1、B2、B3、B4、B5，将之代入式（12），并进行傅里叶逆变换，可得非饱和地基中任意一点（r，θ，z）在时间-空间域内的土骨架位移和应力。

2 数值模拟与分析

2.1 模型退化与验证

为验证模型的正确性，首先将非饱和地基土模型退化为饱和地基土模型，并与文献［8］中的方法进行对比，退化时将本模型中的Sr取0.999，文献［23］中的中间变量As取值为0，其他隧道衬砌以及非饱和地基土参数的选取参考文献［8，26］，如表1所示。表1 中，μs表示饱和状态时的动剪切模量，Ψ 表示土饱和时的内摩擦角。计算单位移动简谐荷载（f0=60 Hz，v0=20 m·s-1）作用下（荷载作用点位置：r=2.75 m，θ=0°，z0=z－v0t=0 m），隧道正下方（r=3.00 m，θ=0°）的动力响应，并与既有模型进行对比，如图2所示。可以发现，本模型计算结果与文献［8］模型的计算结果高度吻合，验证了本模型的可靠性。

表1 隧道衬砌和非饱和地基土计算参数Tab.1 Calculation parameters of tunnel lining and unsaturated soil

图2 模型验证Fig.2 Model validation

2.2 算例分析

选取如表1所示土体参数进行算例的计算。移动简谐荷载v0=20 m·s-1时，不同饱和度状态下隧道底部（r=3.00 m，θ=0°，z0=0 m）土体动位移峰值、动应力峰值和超孔压峰值随频率的变化曲线如图3所示。从图3可以看到，当激振频率f0为0 Hz时，动位移峰值随着饱和度的减小而减小，而动应力峰值随着饱和度的减小而增大。原因在于：土体动剪切模量随着饱和度的减小而增大，该现象与文献［26］中的描述一致。随着激振频率的增大，不同饱和度下非饱和地基土的动位移峰值与动应力峰值趋于一致。此外，从图3 还可以看到，饱和与非饱和地基土中超孔压峰值差异明显。

图3 动力响应随激振频率的变化Fig.3 Change of dynamic response with excitation frequency

图4给出了移动简谐荷载v0=20 m·s-1时，不同饱和度状态下隧道底部（r=3.00 m，θ=0°，z0=0 m）土体超孔压峰值随饱和度的变化曲线。可以看到，在饱和度接近于1.00时，各频率下超孔压峰值随着饱和度的减小而迅速下降。当饱和度下降到0.99时，超孔压峰值下降到饱和土状态下的30%，即在土体饱和度接近于1.00时，饱和度的轻微变化会引起超孔压的剧烈变化。原因在于：随着饱和度的下降，土体中气体由无到以封闭气泡形式存在，最终变为敞开状态［27］，气体存在形式的变化导致了超孔压的急剧变化；气体的体积模量远小于液体与固体的体积模量（液体的体积模量约为气体的13倍），因此轻微的气体增量引起超孔压的剧烈减小。

图4 超孔压随土体饱和度的变化Fig.4 Change of excess pore water pressure withsoil saturation

图5绘制了移动恒定荷载作用下不同位置土体动位移峰值随荷载移动速度的变化曲线。土体的动位移峰值随荷载移动速度的增大而逐步增大，但当移动速度达到100 m·s-1以上时，不同饱和度下的土体动位移峰值相继出现最大值，即荷载移动速度达到土体临界速度。土体临界速度随着土体饱和度的降低而逐渐增大。根据非饱和地基土中剪切波波速表达式ct=ω/Re（kt）［28］，非饱和地基土中剪切波波速随着土体饱和度的降低而增大，故土体临界速度随着土体饱和度的降低而逐渐增大。因此，在高速轨道交通隧道设计时，应考虑土体饱和度对临界速度的影响。