面向煤矿工作面的定位无线传感器网络传输性能优化

方祖浩，赵小虎，王海波，王晶晶

(1.矿山物联网应用技术国家地方联合工程实验室，江苏 徐州 221008;2.中国矿业大学 信息与控制工程学院，江苏 徐州 221008；3.中煤科工集团常州研究院有限公司，江苏 常州 213015；4.天地(常州)自动化股份有限公司，江苏 常州 213015；5.潞安集团 余吾煤业有限责任公司，山西 长治 046100)

0 引言

无线传感网络(Wireless Sensor Network，WSN)在工业上的应用正变得越来越具体化、专一化，出现了用于精确定位的定位无线传感网络(Positioning WSN, PWSN)[1]、用于深入测距的探测无线传感网络(Exploring WSN)[2]、用于实时监控的监测无线传感网络(Monitoring WSN)[3]等。其中PWSN已被应用于煤矿工作面中，煤矿井下环境复杂、事故多发、干扰较强，PWSN必须具有较好的鲁棒性和较长的网络寿命。然而，网络整体性能的提升标准是有效性和可靠性的动态平衡，单方面提升网络可靠性可能会影响网络的传输性能，如网络带宽、传输时间、丢包率等[4]。

为了实现网络传输性能的提升，研究人员提出了许多针对性的传输调度方法，如文献[5]提出文化基因算法(Memetic Algorithm，MA)，通过筛选优质信息，减少网络冗余和传输时延，但该方法过滤掉了大量受损信息，导致接收误差较大、丢包较多；文献[6]提出差分进化人工蜂群(Artificial Bee Colong with Differential Evolution，DE-ABC)算法，通过将信息种群模拟成蜂群，再通过差分计算完成进化过程，该算法能够保证较高的传输准确性和较低的丢包率，但是因为计算复杂度较高，占据过多的网络带宽，使得网络的传输时延较长。

针对上述问题，本文综合考虑传输时间和丢包率这两项性能指标，提出采用结合了粒子群优化(Particle Swarm Optimization，PSO)算法和贪婪算法的保障贪婪调度(Guaranteed Greedy Scheduling，GGS)算法来优化网络传输性能。GGS算法可在保证低丢包率的前提下减少端到端传输时间，优化网络的整体性能。

1 煤矿工作面PWSN

煤矿工作面PWSN模型[7]如图1所示。

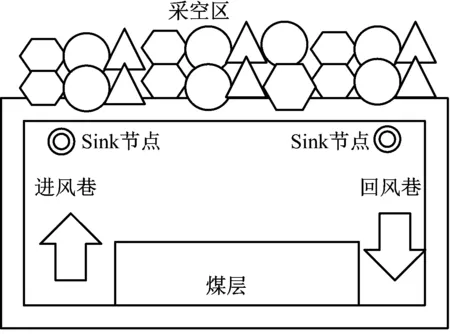
图1 煤矿工作面PWSN模型

在整个工作面上会部署大量节点，节点的类型主要为定位节点及汇聚、发送定位信息的Sink节点[8]。Sink节点部署在信号较好的巷口位置。定位节点部署在移动的液压支架上和矿工身上，以完成对设备和人员的准确定位。设备和人员都处在动态变化的过程中，节点之间的距离也是变化的，因此，网络节点部署是一种变距部署，如图2所示。这种变距节点部署会延长网络对距离的判断时间，增加多跳次数，影响网络传输性能[9]。

图2 变距节点部署

2 数学模型

通过建立数学模型定义报文种群在信道上有序排队的过程，这样的有序排队不仅能够减少堵塞和传输时间，也在一定程度上避免了因共享信道而导致的丢包。

为了便于讨论，引入以下数学符号：信息集I={I1,I2,…，In},n为报文数；信道集M={M1,M2,…,Mm},m为信道数；报文Ii在信道Mk上的传输时间为Ai,k，1≤i≤n,1≤k≤m；报文Ii在信道Mk上的开始时间为Si,k；报文Ii在信道Mk上的结束时间为Ri,k；最大传输时间Cmax=max(Ri,m|i=1,2,…,n)。

n条报文在m条信道上传输时具有以下约束：① 每条信道在某一时刻只能发送1条报文。② 在下一个信道被释放前，报文在当前信道上完成传输后将被堵塞在当前信道上。基于上述描述，给出数学模型：

(1)问题目标为minCmax，即最小化最大传输时间。

(2)若后续信道k+1非空闲，则报文被堵塞在信道k上，直至信道k+1空闲为止。该传输问题可用式(1)—式(6)进行描述。

S1,1=0

(1)

R1,1=A1,1

(2)

(3)

Ri,1=max(Ri-1,1+Ai,1,Ri-1,2)

i=2,3,…,n

(4)

Ri,k=max(Ri,k-1+Ai,k,Ri-1,k+1)

i=2,3,…,nk=2,3,…,m-1

(5)

Ri,m=Ri,m-1+Ai,mi=2,3,…,n

(6)

上述数学模型可以很好地反映PWSN一维结构的特点：① 多节点转发并传输信息，信息在节点上的传输是并行的，节点之间相互无影响。② 多信道传输信息，信息在信道上的传输是串行的，若前一个信道发生堵塞，则会影响后续信道的传输。

3 GGS算法

GGS算法是保障算法和贪婪算法的叠加。保障算法采用PSO算法。在PWSN中，从底层汇聚上来的数据信息是杂乱无序的，如果不加排列就进行传输，会导致网络拥塞及带宽浪费，降低网络传输效率。通过PSO算法使报文在传输前就保持有序状态，在信道中依次传输，可提升网络传输效率，减少网络传输时间[10]。

贪婪算法指的是多层次迭代算法[11]。通过设置最优解的方法，让报文进行多层次迭代和局部搜索[12]，使其逐渐向最优解逼近，这样就能按照设定的最优解对报文进行优先级排队，按照优先级顺序进行传输调度，保证有效信息不会遗漏，同时过滤掉无用信息，提高传输调度效率。

GGS算法流程如图3所示。利用保障算法完成对种群的初始化后，开始利用贪婪算法对网络进行优化[13]。

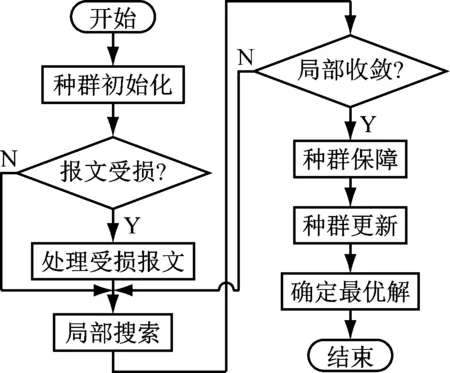
图3 GGS算法流程

3.1 种群初始化

种群初始化的目的是将无序、混乱的报文信息种群进行有序处理，得到稳定、有序的报文种群。具体初始化过程如下：

(1)产生初始解：λ={λ1,λ2,…，λn},λn为种群中的第n个个体。

(2)设置断点h(1

(3)根据空闲时间和堵塞时间，通过以下方法选择合适的报文：从λ″中依次取出报文λj(j=h+1,h+2,…,n)并假定λj为λi的紧邻后续报文；用式(7)计算λj作为λi的紧邻后续报文进行传输时所产生的空闲时间和堵塞时间的总和sumj；取sumj值最小的报文λj作为λi的后续紧邻报文，此时λ″={λ1,λ2,…,λh}+λj。

(7)

3.2 关键条件设定

网络优化的目的是降低丢包率，减少传输时间，对丢包率和传输时间有直接影响的关键条件是受损报文。若将受损报文加入队列，则会延长传输时间；若将受损报文排除出队列，则会影响报文交付率，即增大丢包率。对受损报文的处理将直接决定网络的整体性能。因此，设定关键条件是报文是否受损，若没有受损，则直接排入队列，若已受损，则要对受损报文进行处理。受损报文处理过程如下：首先，对于λ={λ1,λ2,…，λn}，以d作为损坏的报文数，随机从λ中选取d个报文构成序列λ′，将λ′中的报文依次插入使λ的传输时间最小的位置，然后按此方式，每个个体产生N个邻域个体，取N个邻域个体中Cmax值最小的序列λ″,若λ″的解较损坏前的λ的解没有改善，则调整受损报文数为d+r(r为大于1的整数)，继续上述操作，否则用λ″更新λ。

3.3 局部搜索

局部搜索的目的是找到邻域内的最优个体，然后按序排列。多层次迭代方法会让得到的解更加精确化，迭代的次数、层数越多，得到的解就越精确。每一层迭代的思路是一致的，以前3层迭代为例，展示多层次迭代的主要思路。设λ={λ1,λ2,…，λn}的解为Cmax(λ)，按以下步骤进行分层迭代。

(1)第1层迭代：设置迭代层数为1，受损报文数为d，对λ进行受损判断和处理，得到受损后的排列及受损报文序列；将受损报文依次插入使传输时间最小的位置，得到最优邻域序列λ″,其解为Cmax(λ″)。

(2)第2层迭代：设置迭代层数为2；设置受损报文数d=d+r(r>1),再循环到第1层迭代的操作。

(3)第3层迭代：设置迭代层数为3；设置受损报文数d=d+r′(r′为大于r的整数),再循环到第1层迭代的操作。

历经3次迭代后，个体的效果如果没有进步，则认为个体已达到局部收敛的状态，通过种群保障的方法跳出局部收敛。

3.4 种群保障

历经多层次迭代后，需要判断优化过的种群是否收敛，若种群没有收敛，则继续重复迭代过程；若种群已收敛，则要对种群进行保障操作。此时，需要用到PSO变异算法。PSO变异算法主要是对种群个体进行交换和插入。算法在变异时采用组合策略，即可以单独交换、单独插入，也可以交换插入。

交换操作：随机选择2个个体λa,λb，a≠b，将λa,λb进行交换。

插入操作：随机选择2个个体λa,λb，a≠b，|a-b|>1,将λa插入λb所在位置之后，若ab,则得到序列λ′={λ1,λ2,…,λb,λa,λb+1,…,λa-1,λa+1,…,λn}。

通过交叉和变异操作，能够让已经收敛的种群跳出收敛，并在传输过程后期再次有序排列，可减少接收过程中的丢包和接收时间。

3.5 种群更新

在完成种群保障后，需要对种群进行更新，得到最优解。种群更新策略：

λi=λi⊗Pbesti⊗Gbest

(8)

λi=PR(λi,P)

(9)

式中：⊗表示交叉操作；Pbesti表示个体λi当前时刻的最优解；Gbest表示种群当前时刻的最优解；P表示种群中所有个体；PR(λi,P)表示从个体λi开始，将种群中的所有个体进行路径重连接，即重新选择路径。

4 仿真分析

考虑到工作面环境恶劣、空间狭长并且存在大型设备的电磁干扰，使得煤矿传感数据存在缺失、异常、含噪声明显等特征，故在仿真时选择满足上述特征的数据集。经过比较，选择公共数据集Taillard[14]作为仿真数据集。选择数据集Taillard中不同规模的数据作为初始报文种群，利用GGS算法、MA、DE-ABC算法对报文进行处理，得到端到端传输时间和丢包率，并进行比较。其中，MA没有用到PSO算法的保障，DE-ABC算法缺少多层次迭代的贪婪过程。

4.1 保障算法验证

未使用保障算法时的初始种群和使用保障算法得到的种群分别如图4和图5所示。对比发现，未使用保障算法的种群在信道上排列无序、混乱；使用保障算法后的种群在信道上呈线性排列，更加有序和稳定。

4.2 贪婪算法验证

对不同数据规模下的端到端时间进行仿真。粒子群大小为100、信道数为20时的部分仿真结果见表1，在此数据规模下，迭代次数为100×20=2 000。

图4 未使用保障算法时的初始种群

图5 使用保障算法初始化后的种群

表1 端到端时间仿真结果(100×20)

为了避免实验数据的偶然性，保证结果的准确性，设粒子群大小为100、信道数为50，部分仿真结果见表2。

根据表1和表2的数据得到图6。从图6可看出，当种群数量为100时，GGS算法的传输时间比其他算法少1～2 s；随着种群数量不断增加，GGS算法的端到端时间增长明显慢于其他算法，当种群数量达到较大规模时，GGS算法在传输时间方面的性能优势更明显。

表2 端到端时间仿真结果(100×50)

图6 端到端时间随种群数量变化曲线

4.3 丢包率分析

因为仿真是在同一数据规模下进行，所以丢包数就可反映最终的丢包率情况。当迭代次数过小时，不同算法的丢包数差异很小，因此，直接跳过低频次迭代过程，设粒子群大小为100、信道数为50，部分丢包数仿真结果见表3。

表3 丢包数仿真结果(100×50)

根据表3的数据得到图7。可以看出：在传输过程的起始阶段，GGS算法的丢包数明显少于其他算法；随着传输过程的进行，GGS算法的丢包数依然维持在较低水平，验证了GGS算法在丢包率方面的性能优势。

图7 丢包数随种群数量变化曲线

5 结论

针对煤矿工作面PWSN网络存在的网络传输时间较长、丢包率较高的问题，提出了以PSO算法为保障、以多层次迭代算法作为贪婪算法、逐渐向最优解逼近的GGS算法。通过对比试验，得出以下结论：

(1)在传输过程的起始阶段，GGS的丢包数明显少于其他算法；随着传输过程的进行，其丢包率依然维持在较低水平。通过GGS算法的优化，网络的可靠性得到增强。

(2)当种群数量为100时，GGS算法的传输时间比其他算法少1～2 s。当种群数量达到较大规模时，GGS算法在传输时间方面的性能优势更明显。

(3)GGS算法优化了网络的传输调度过程，在控制丢包率的前提下缩短了传输时间，提升了网络的整体性能。