一种新的VANET网络链路丢包率估计算法

陈强伟,赵建华,杨雪芹2,张珊珊

(1.西安工业大学 电子信息工程学院,西安 710021；2.西安邮电大学 通信与信息工程学院,西安 710121)

1 引 言

车载自组织网络(Vehicle Ad-hoc Network,VANET)[1-2]是一种快速移动的带宽多跳无线网络，用于实现移动过程中车辆与车辆之间的通信、车辆与路边基础设施之间的通信。VANET在网络安全、移动互联网中扮演重要的角色。

VANET属于无线网络的范畴，有着复杂多变的环境和分布区域广泛的拓扑结构，而无线网络中无线链路特性和无线信道特性将直接对上层协议的性能的执行起到重要影响。在VANET网络中，由于汽车的快速移动变化、车辆相对速度的不同及路况条件的复杂、城市交通道路上建筑物的遮蔽等，使得在车辆与车辆之间进行无线通信超出了通信范围或信号被遮蔽，车辆间不能直接进行信息交换。而且在城市环境下，车辆密度过大，这就导致节点对无线信道的频繁竞争，从而使得实际带宽低于理论值。此外,信道还存在多径衰落、多普勒效应遮蔽效应等问题，因此，误码率、丢包率[2]较高，从而导致无线链路质量不佳，而且无线通信带宽受到限制约束。因此，无线链路质量的好坏可以根据链路丢包率的大小进行评定。

本文提出一种新的基于贝叶斯估计的后验期望估计(Posterior Expectation Estimation，PEE)算法[3]研究链路丢包率，通过实验证明了所提算法的优越性。

2 链路丢包率估计算法

对于链路丢包率的实时估计，不仅有利于在无线网络链路中信息的传递，更决定了对上层传输控制协议应用[4]的执行。因此，对链路丢包率的估计，选择相应的算法是非常重要的。

2.1 PEE算法介绍

后验期望估计，亦称参数θ的后验期望估计，其定义如下：

设γ是总体P中的未知参数，γ∈Γ(参数空间)，为了估计参数γ和预测总体P，可以从这个总体中抽取样本P1，P2，…，Pn，p=(p1，p2，…，pn)为样本观察值，根据参数γ的先验信息选择一个先验分布π(γ)，再根据贝叶斯定理可以得到γ的后验分布π(γ|p)，然后根据这个后验分布对参数γ进行估计以及对总体P进行预测。寻找一个统计量的观察值，记作γ′(p)，用γ′(p)去估计γ。

2.1.1PEE的损失和风险函数

对于PEE算法估计参数好坏也要考虑到标准问题，从而寻找到最好的估计，在估计的过程中会用到构建损失函数以及风险函数[5]来描述。下面给出几个定义：

在参数γ取值范围Γ(参数空间)上，定义一个二元非负实函数L(γ,γ′)，表示γ′去估计γ时γ′与γ的不同而引起的损失，通常这个损失是非负的，因此L(γ,γ′)≥0。

常见的损失函数有差值平方损失函数L(γ,γ′)=(γ-γ′)2和差值绝对值损失函数L(γ,γ′)=|γ-γ′|，在这里PEE的损失函数采用的是差值平方损失函数。

对于损失函数L(γ,γ′)，用γ′(p)去估计γ时，定义了一个用γ′(p)的概率与损失函数L(γ,γ′)的乘积之和，即是L(γ,γ′)的数学期望，用公式表示为

(1)

称为γ′(p)相应的风险函数。

对于PEE来说，它的相应的风险函数为

Aγ′(p)(γ)=E[L(γ,γ′)]=E[(γ-γ′)2]=

(2)

对于好的估计，相应的风险函数应尽量小。

下面介绍两个定义：

定义1：如果γ*′(p)在估计类M中，使得等式

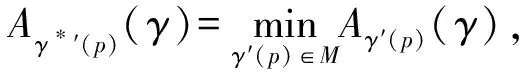
(3)

成立，则称γ*′(p)是M估计类中的一致最小风险估计。

定义2：如果γ*′(p)使得

(4)

成立，则称γ*′(p)是针对π(γ)的贝叶斯的解。

2.1.2原理介绍

由2.1.1节可知，PEE算法的参数估计γ就是后验期望E(γ|p)，下面简单证明。因为对于PEE算法其损失函数是L(γ,γ′)=(γ-γ′)2，类比于相应风险函数，就有后验风险函数

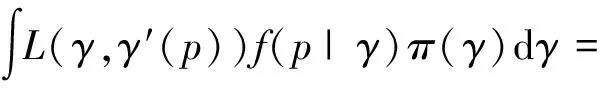
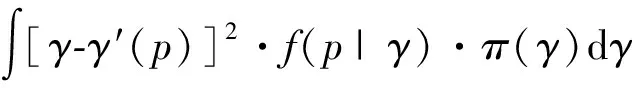
(5)

式中：π(γ)是γ的先验分布函数，f(p|γ)是样本p对γ的条件密度函数。

当PEE的后验风险函数最小时，即γ*′(p)=E(γ|p)。

2.2 其他估计原理

2.2.1最大似然估计

通常来说，在设定的参数γ为γ0时，并且与数据P的模拟复合的程度就可以用数据P的条件概率p(p|γ=γ0)进行计算，这个概率越大，γ0与数据P的模拟复合相似就越高。

对于已经给定的γ，数据P的条件概率p(P|γ)称γ的似然度或者叫做似然因子，记作L(γ|P)∝p(P|γ)。

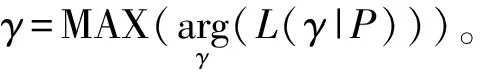
2.2.2期望传输次数估计

期望传输次数(Expected Transmission count，EXT)估计算法是用来估计无线网络链路丢包率的一种常用的估计算法，它通过发送大量的网络探测包，用传输失败的网络探测包的数量比上总的发送网络探测包的数量来获得链路的丢包率。但是，用这种算法估计链路丢包率需要发送大量的网络探测包才能保证检测出真实的无线链路质量的好坏，EXT的值越小，无线链路质量越好。

在VANET网络中，某条链路l从发送端A以每秒恒定数量发送探测包，通过无线管道链路向接收端B发送，在时间间隔ΔT内，发送端A发送Mi个探测包，接收端B接受mi个探测包，则

(6)

3 链路丢包率的模型建立

3.1 大数据统计

利用VANET的实际条件进行了相应的模拟测试，并获得了相关的丢包率的概率密度分布(Probability Density Function，PDF)曲线，如图1所示。

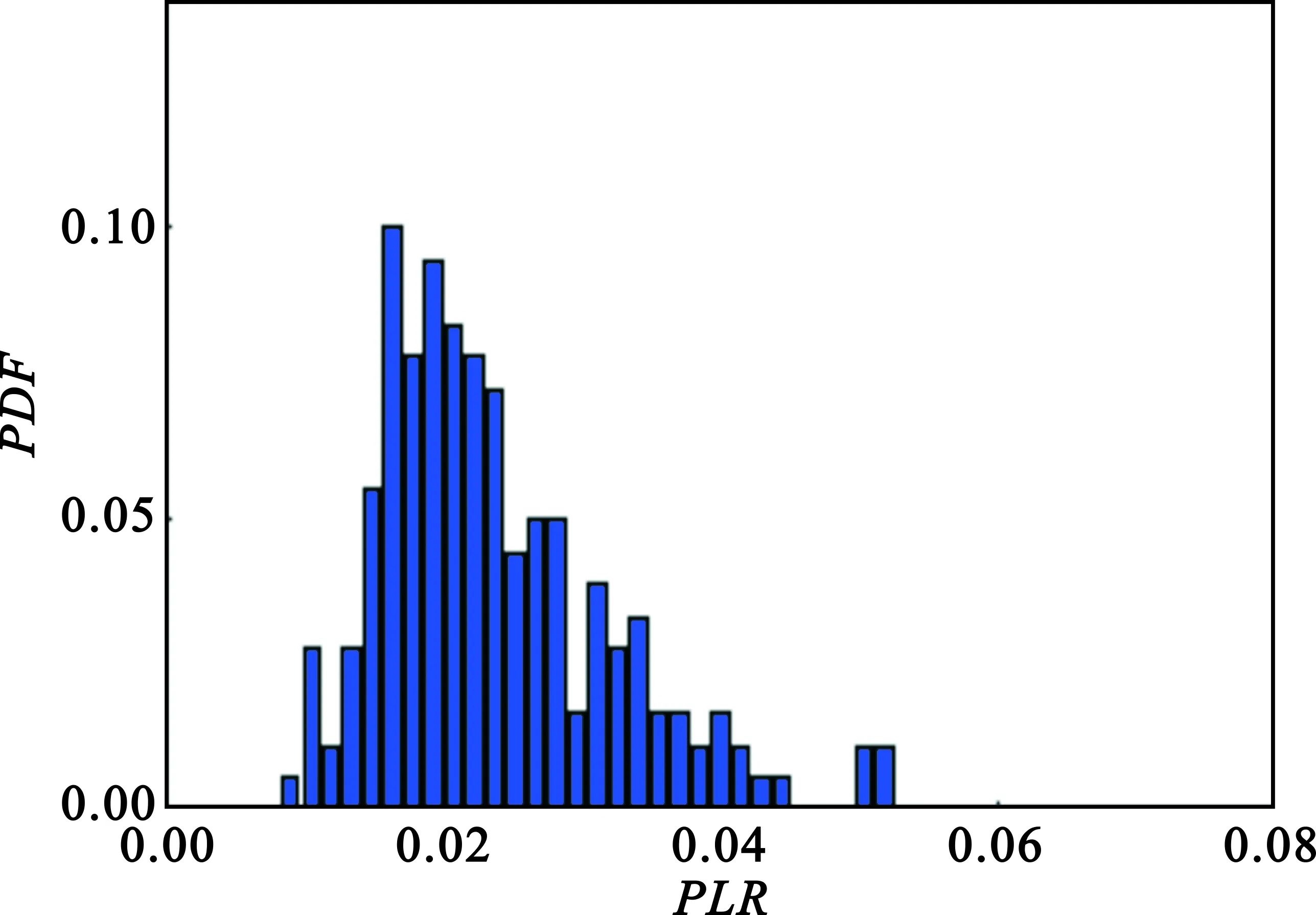
(a)节点距离0～15 m

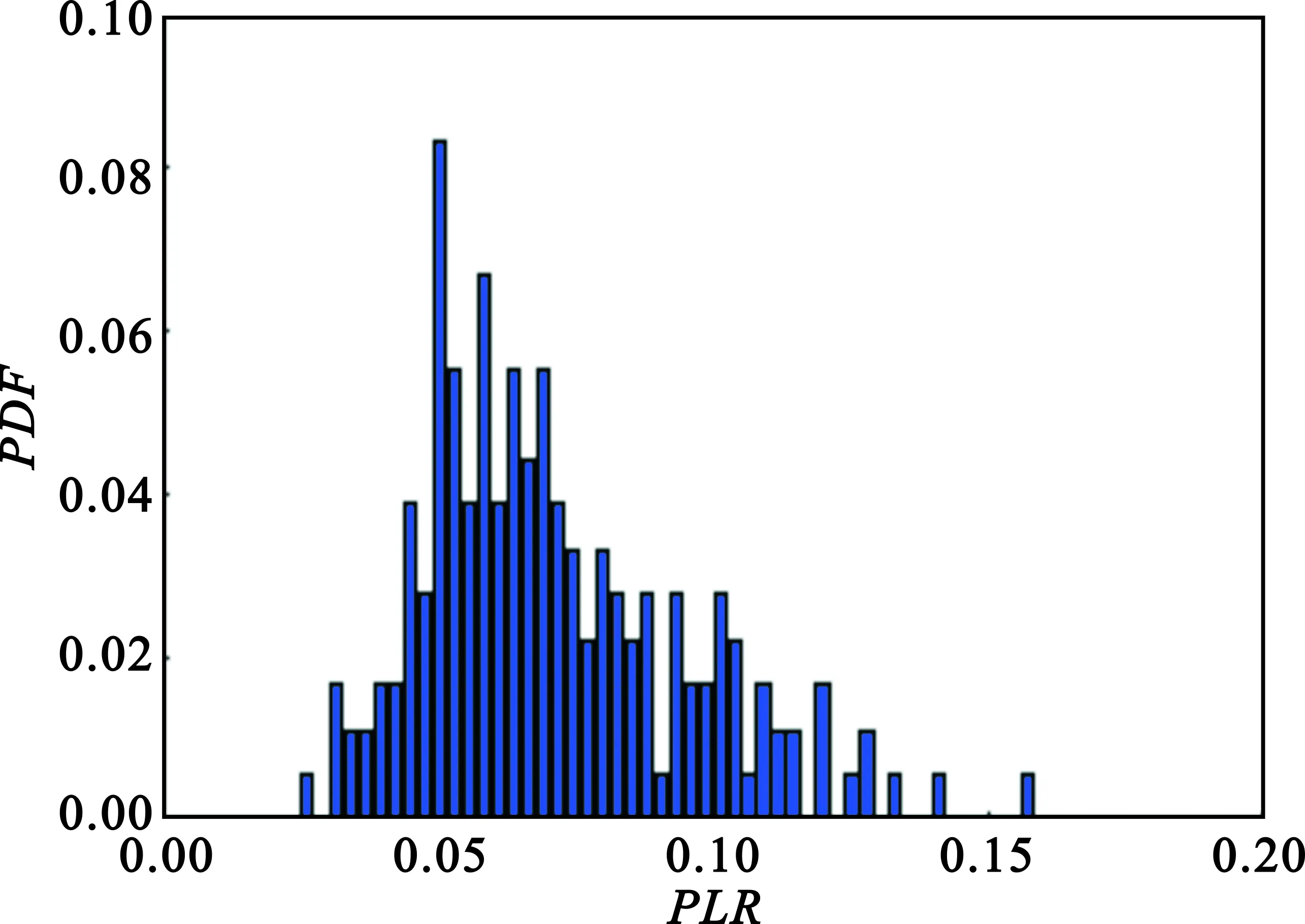
(b)节点距离30～40 m图1 节点距离的丢包PDFFig.1 Packet lost PDF with node distance

从这些数据可得到，当节点距离在0～15 m时，丢包率处在0～0.07之内，集中在0.02左右；当节点距离在30～40 m内时，丢包率处在0～0.2内，最高可到达17%的丢包结果。分析可知，车辆间的距离对VANET的链路丢包率的影响十分显著。

3.2 链路丢包率函数模型优化

由3.1节知，大数据统计的结果反映了样本信息p和先验概率分布π(γ)和条件概率分布PDF(p|γ)，因此函数模型优化可以根据贝叶斯统计方法进行，样本的全部目的是完成由先验概率与条件概率分布到后验概率分布的转换，从而完成对链路丢包率估计与预测的认识的改变，这个过程可以用图2表示。

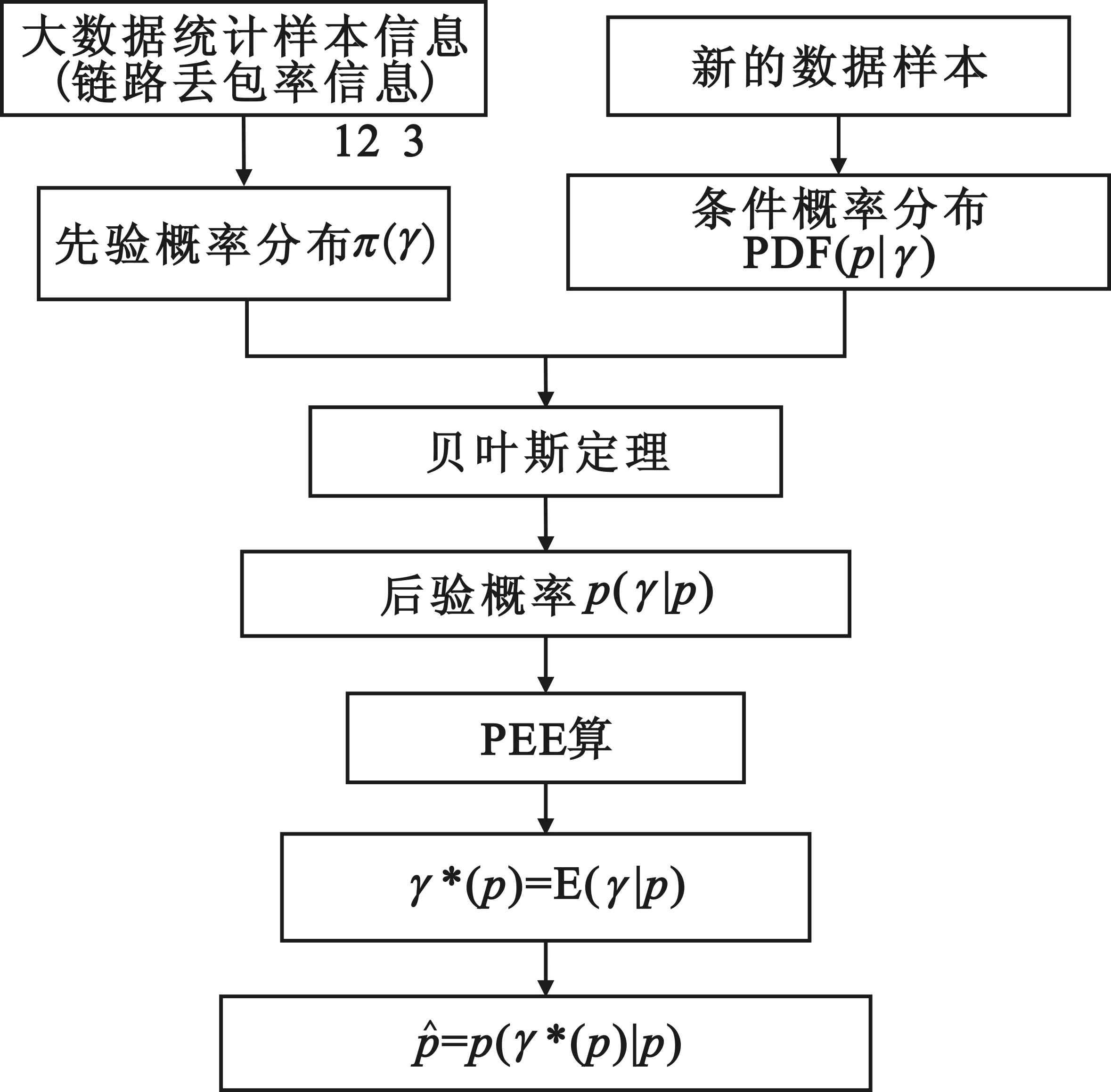
图2 PEE算法的整体流程图Fig.2 Overall flow chart of PEE algorithm

流程可描述如下：

(1)将未知参数看成随机变量(或者随机向量)，记为γ。于是当γ已知时，样本p1，p2，…，pk的联合分布密度p(p1，p2，…，pk,γ)就看成是p1，p2，…，pk对γ的条件密度，记为p(p|γ)。

(2)用π(γ)表示π(γ)的先验分布，一般根据以往对参数知识γ来确定先验分布(经常用于表示先验知识)，在这里，链路丢包的先验概率服从高斯分布，记作π(γ)～N(μ0，σ0)。

(3)利用先验分布π(γ)和条件分布密度p(p|γ)，可以求出p1，p2，…，pk与γ的联合分布以及样本数据p1，p2，…，pk的分布，于是就可以利用两者求得γ对p1，p2，…，pk的条件分布密度，也就是利用贝叶斯公式求得后验分布密度p(γ|p)的过程。

(4)由后验概率密度p(γ|p)，结合PEE算法，得到贝叶斯解γ*(p)=E(γ|p)。

3.3 链路丢包率的模型预测

链路丢包率的实时预测对VANET网络中的通信质量和通信信息的传递起着非常重要的作用。在预测到该通信链路的丢包率超过正常通信所允许的丢包率时，就需要选择其他链路通信或改变原有的通信路由协议，让其丢包率符合正常的通信范畴，这样，整个VANET网络中的通信过程稳定性和健壮性就得到了保证。

由3.2节知，以其链路丢包率的模型优化为基础、以其动态的模型为研究对象的时间序列的预测方法，可以称作贝叶斯预测。贝叶斯预测不仅仅使用了模型信息及样本信息，还用了先验概率的分布信息，这也是不同于非贝叶斯预测的标志。

在预测过程中，对于总体分布的位置参数预先设定一个先验概率分布，这个概率分布可以根据以前的数据、经验给出，也可以完全根据决策者的主观意识给出。这样将先验概率分布、总体分布通过贝叶斯公式得到后验概率分布，最后通过后验概率分布对链路丢包率目标进行预测，其预测过程如图3所示。

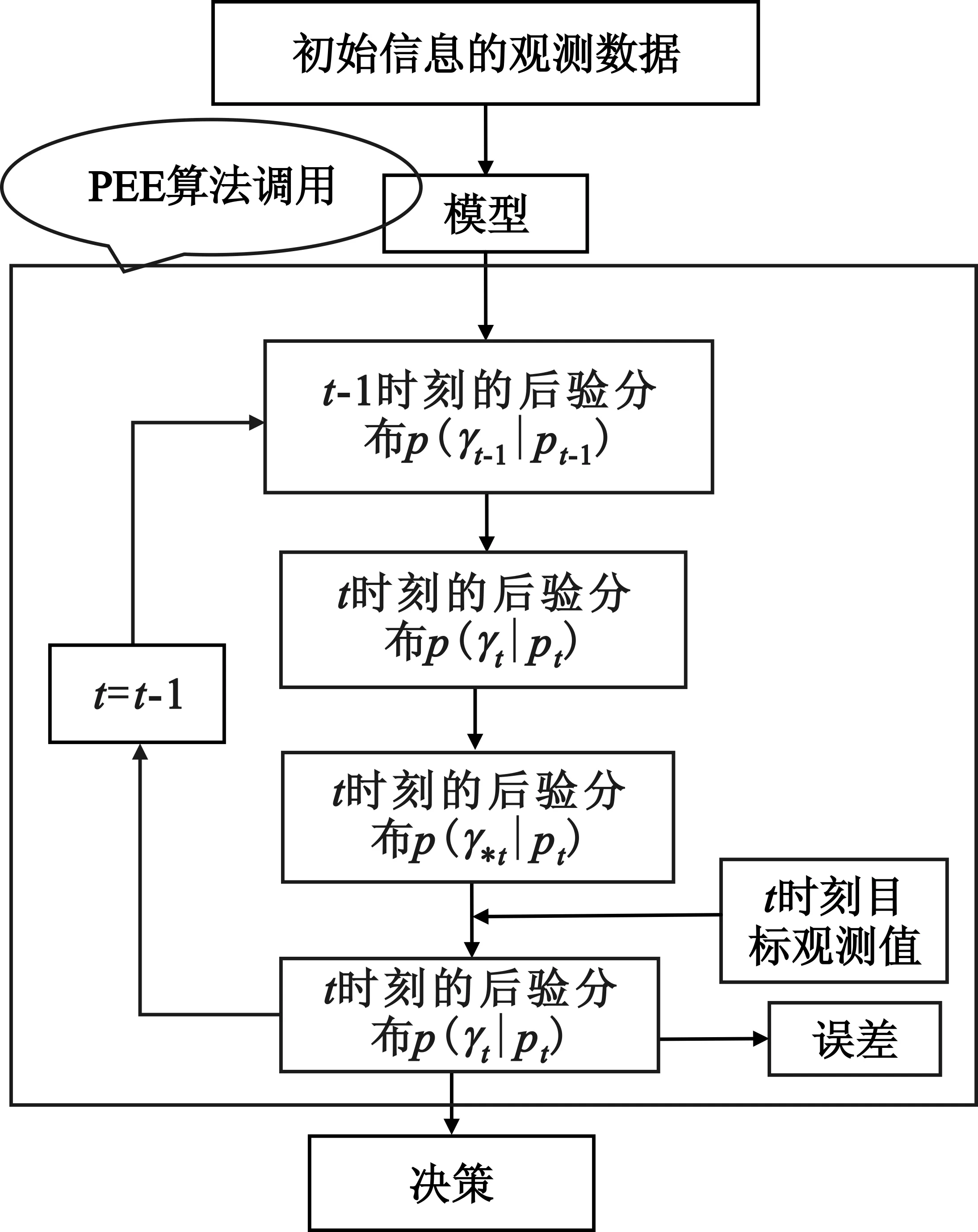
图3 目标数据的预测流程图Fig.3 Flow chart of forecasting the target data

4 实验结果及分析

4.1 数据整理

由3.1节知，根据大数据收集到的链路丢包率的结果数据，可绘制出链路丢包率PDF图像直方图，进行数据的整理。在这里，数据与高斯模型进行叠加混合(Gaussian Mixture Model，GMM)，形成了如图4所示的曲线。因此，链路丢包率的PDF服从于高斯分布，记作p～N(γ),其中γ=(μ,σ)。

(a)距离0～15 m

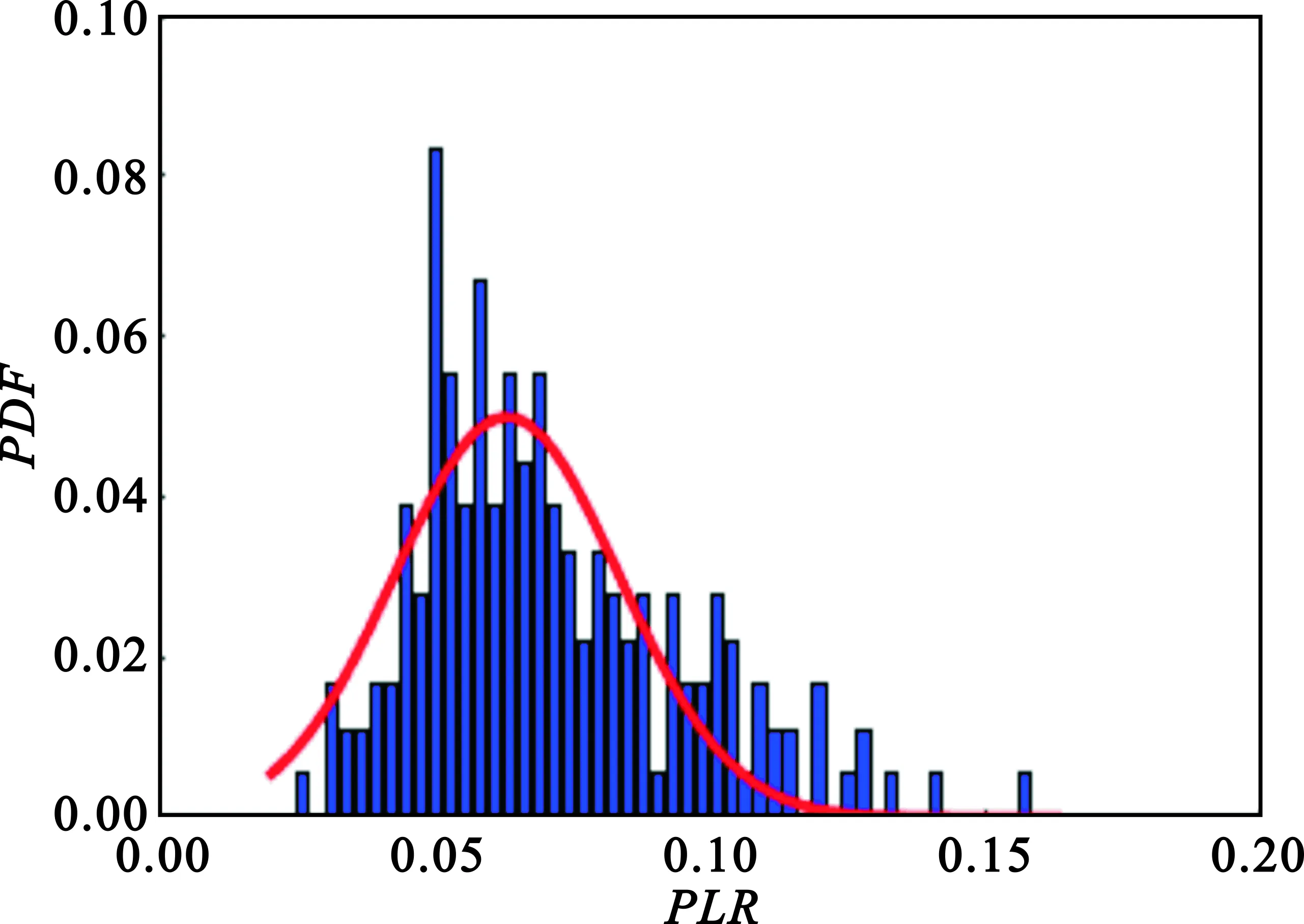
(b)距离30～40 m图4 GMM曲线Fig.4 GMM curve

4.2 结果分析

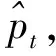
这里给出几个判别比较定义[7-8]：

(1)Predict-Original(PO)，即预测数据和原始数据的误差平方和：

式中：Pk是预测数据，Ok是原始数据。

(2)Predict-Value(PV)，即预测数据与原始数据均值之差的平方和：

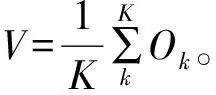
(3)Original-Value(OV)，即原始数据与原始均值的平方和：

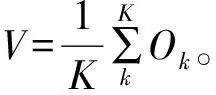
(4)Predict-Proportion(PP)，即预测程度系数，越接近1，说明预测数据与原始数据越接近。

通过对图5和图6进行数据分析，整合得到表1。

图5 距离0～15 m的PEE预测图像Fig.5 PEE prediction with 0～15 m distance

图6 距离0～15 m的算法预测比较Fig.6 Algorithm prediction comparison with 0～15 m distance

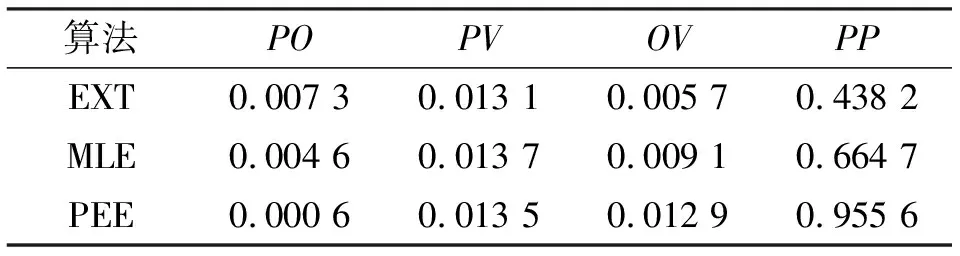
算法POPVOVPPEXT0.007 30.013 10.005 70.438 2MLE0.004 60.013 70.009 10.664 7PEE0.000 60.013 50.012 90.955 6

处理表1中的结果值可得到更直观的分布直方图，如图7所示。

图7 距离0～15 m算法数据比较图Fig.7 Histogram for algorithm data comparison with 0～15 m distance

根据表1生成的图7更加直观地显示出特征结果，能得到PO的值，PEE算法好于MLE，优于EXT算法预测得到的丢包率。PEE算法的PP值更接近于1，说明预测的效果与真实值丢包率接近。在图6中，PEE算法的预测丢包率的数据误差曲线的波动小于MLE算法的预测丢包率的数据误差曲线波动，远小于EXT算法的预测丢包率误差曲线的波动，这正好反映了预测程度系数值。

对图8、图9的数据进行整理，得到如表2所示的3种算法预测链路丢包率。

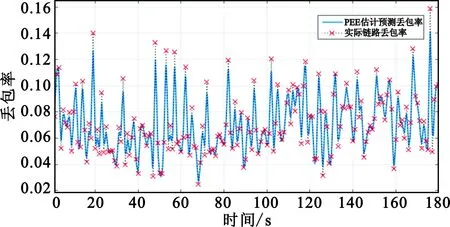
图8 距离30～40 m的PEE预测图像Fig.8 PEE prediction image with 30～40 m distance

图9 距离30～40 m算法预测比较Fig.9 Algorithm prediction comparison with 30～40 m distance

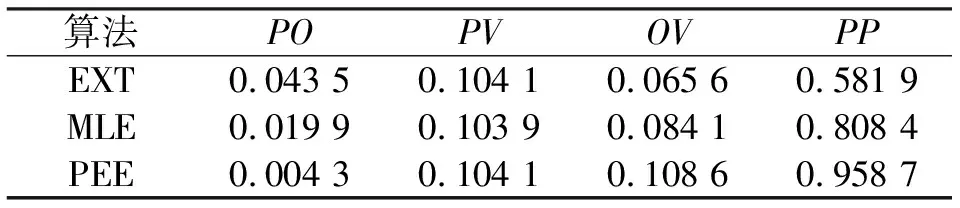
算法POPVOVPPEXT0.043 50.104 10.065 60.581 9MLE0.019 90.103 90.084 10.808 4PEE0.004 30.104 10.108 60.958 7

处理表2中的结果值可得到分布直方图，如图10所示。

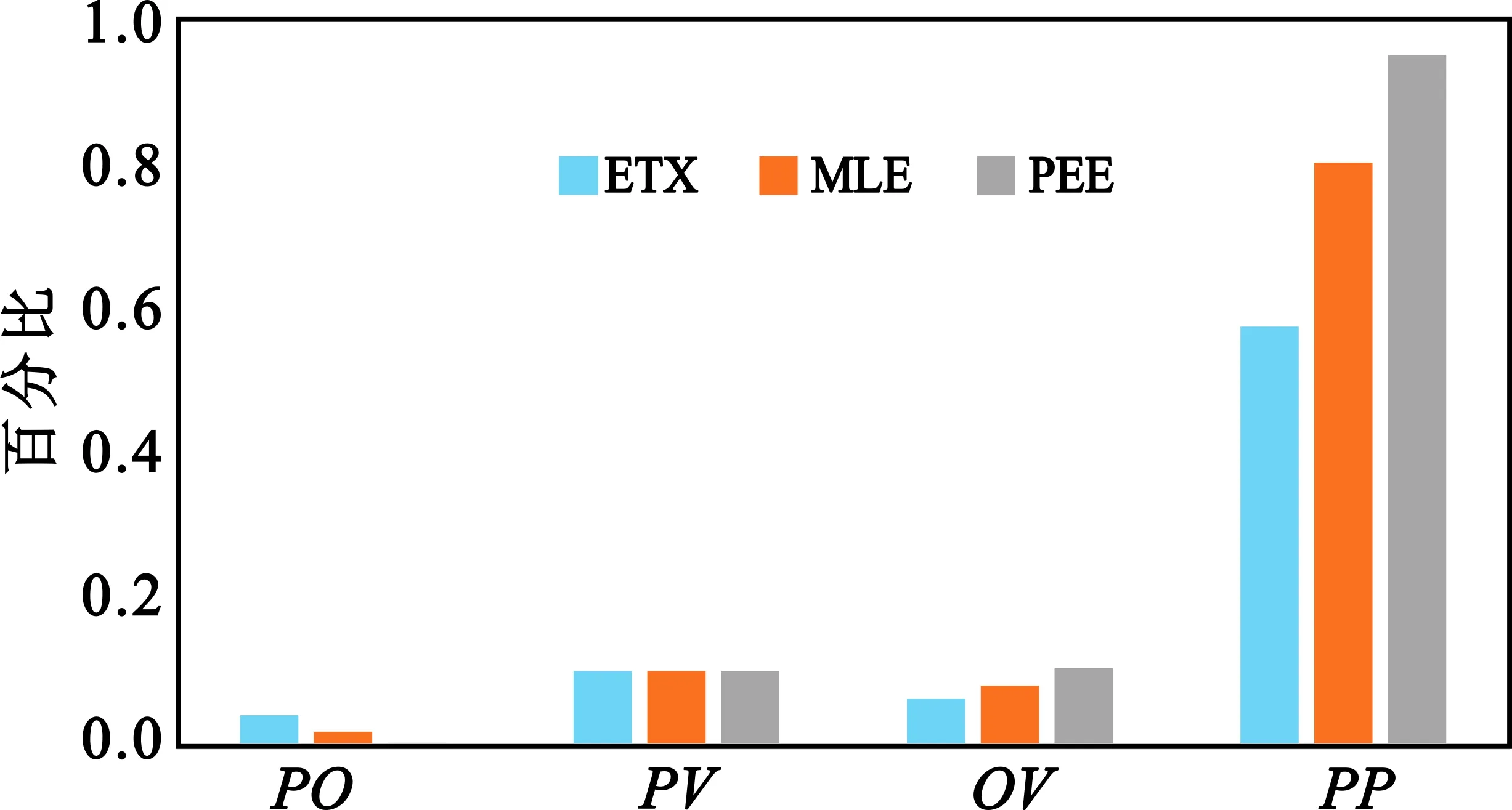
图10 距离30～40 m算法数据比较图Fig.10 Histogram for algorithm data comparisonwith 30～40 m distance

通过数据的比较可知，PEE算法得到的PO值小于MLE算法得到的PO值，也小于EXT算法得到的PO值；而对于预测程度系数来说，PEE算法得到的PP值大于MLE算法得到的PP值，也大于EXT得到的PP值，而且PEE算法得到的PP值趋近于1。在图9中，PEE算法的预测丢包率误差曲线波动小于MLE算法的，远小于EXT算法的，故可以得到在距离为30～40 m时PEE算法的优越性最好。

由图5和图8可知，在距离0～15 m通信范围，预测丢包率平均在0.025左右，最高不超过0.05；而在距离30～40 m通信范围内，预测丢包率平均在0.08左右，远大于0.025。这也就说明了在实际的通信过程中丢包率和距离有关，距离越大，丢包率越大，相应的无线链路的质量就差。

5 结束语

对于VANET中无线链路质量的好坏，其最为关键的一项就是链路丢包率的大小。由图表数据分析知，车辆之间的距离对无线链路丢包率的影响较大，间接影响了无线链路的质量，造成了VANET网络通信非常严重的信息传输丢失的问题。

虽然通过PEE算法可以快速准确地估计预测链路丢包率，但本文所选用的是非常理想的场景条件，对于复杂多变的实际道路场景，此算法还要进行深入探索，考虑更多的影响因素，这样，研究成果才能发挥最大效能。