第10届全球绝对重力仪关键比对相对重力测量

刘善良, 吴书清, 冯金扬, 王启宇,吉望西, 粟多武, 李春剑

(中国计量科学研究院,北京 100029)

1 引 言

绝对重力测量在计量学、惯性导航、资源勘探、地质反演及地震监测等方面有着广泛而深远的意义[1]。高精度绝对重力仪是直接测量重力加速度值的精密仪器,为了更精确地测量绝对重力值,需要定期进行绝对重力仪比对,以验证其测量不确定度的有效性并确保其测量量值的溯源性。2017年10月至12月,中国计量科学研究院作为主导实验室进行了第10届全球绝对重力仪关键比对(CCM.G-K2.2017)。由于不同绝对重力仪测量的重力值对应于不同的参考高度,需要通过相对重力测量将重力值归算到同一高度进行比较[2]。归算需要精确测定点位重力垂直梯度值,这直接影响到最终关键比对参考值(KCRV)的不确定度[3],对于建立全球重力测量原点和国家重力计量基准体系具有十分重要的意义。

2 比对相对重力测量

此次绝对重力仪国际关键比对在中国计量科学研究院昌平院区地下实验室进行,比对实验室具有较好的隔振地基,振动干扰较小,温湿度比较稳定,符合比对的条件。根据比对技术协议[4]:需要用相对重力仪测量用于比对的9个点位的重力垂直梯度值。

2.1 相对重力测量原理

相对重力测量是使用相对重力仪测定2点间的重力差值的技术和方法。通过相对重力仪测量的计算公式可以表示为:

g=gm+∑gi+d(t)

(1)

式中:gm为相对重力仪m的重力值读数;∑gi为不含漂移的各项改正;d(t)为相对重力仪测量时间t对应的的漂移改正,主要改正有以下几项:

1) 固体潮改正:地球固体表面受到太阳和月球的吸引力作用使重力值发生周期性的变化即为固体潮影响。固体潮的理论模型计算可以达到微伽级精度,相对重力仪的数据采用Tsoft[5]软件进行固体潮改正。

2) 气压改正:地球外部的大气层具有一定的质量,会对周围的质点产生引力使相对重力仪的重力值读数产生变化。这种影响只能通过经验公式进行改正:

C(p)=0.3(p-pn)

(2)

式中:p为大气压观测值;pn为标准大气压,3 hPa的大气压变化可以引起1 hPa的重力变化。

3) 仪器高改正:由于重力仪的传感器所在位置不是归算高度,因此需要将测量结果转化到归算高度,这一过程称之为仪器高改正。计算公式为:

δg=γg×Δh

(3)

式中:γg为点位重力垂直梯度;Δh为仪器传感器高度与归算高度之差。

4) 漂移改正:把相对重力仪放在台站固定点位上,每隔一定的时间进行一次读数,结果是数值在不断变化且时间间隔越长,读数相差越大,就像重力仪的零位置在不断地变化,这种现象称为零点漂移,简称零漂。零漂改正计算公式为:

Δg=k×Δt

(4)

式中:k为线性漂移常数;Δt为观测时间。

2.2 相对重力测量方案

参与此次比对相对重力测量的3台相对重力仪分别是:2台Burris和1台CG-6相对重力仪,所有相对重力仪都严格按照主导实验室比对协议进行测量,且都独立完成全部测量。共有9个点位参与此次比对,需要用相对重力仪测量9个点位的重力垂直梯度。考虑到比对实验室附近靠近山体且处于地下空间,重力值随高度的变化呈现出非线性规律,即梯度不能等效为常数处理。以往比对梯度测量通常选用3个高度进行二次拟合,为了提高拟合精度,此次比对选用4个高度进行二次拟合。

图1和图2为相对重力仪点位梯度测量方案,图中高度为相对重力仪传感器距离地面的高度,由于不同类型的相对重力仪传感器高度不一样[6],所以图1和图2的实测高度对应不一致。测量时每个点位重力垂直梯度由3台相对重力仪独立完成,每台相对重力仪完成2个循环共计26次测量。对于不同的高度测量,受限于相对重力仪的传感器高度,需要结合不同高度的三角架进行组合测量,测量过程示意图如图3所示。

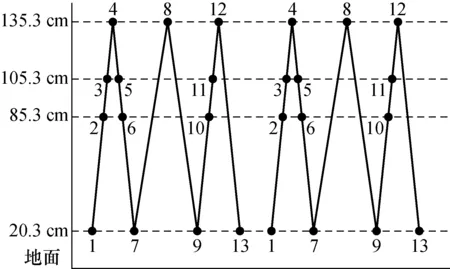
图1 相对重力仪CG-6 S032点位梯度测量示意图Fig.1 Vertical gradient measurements at a station for Scintrex CG6 S032

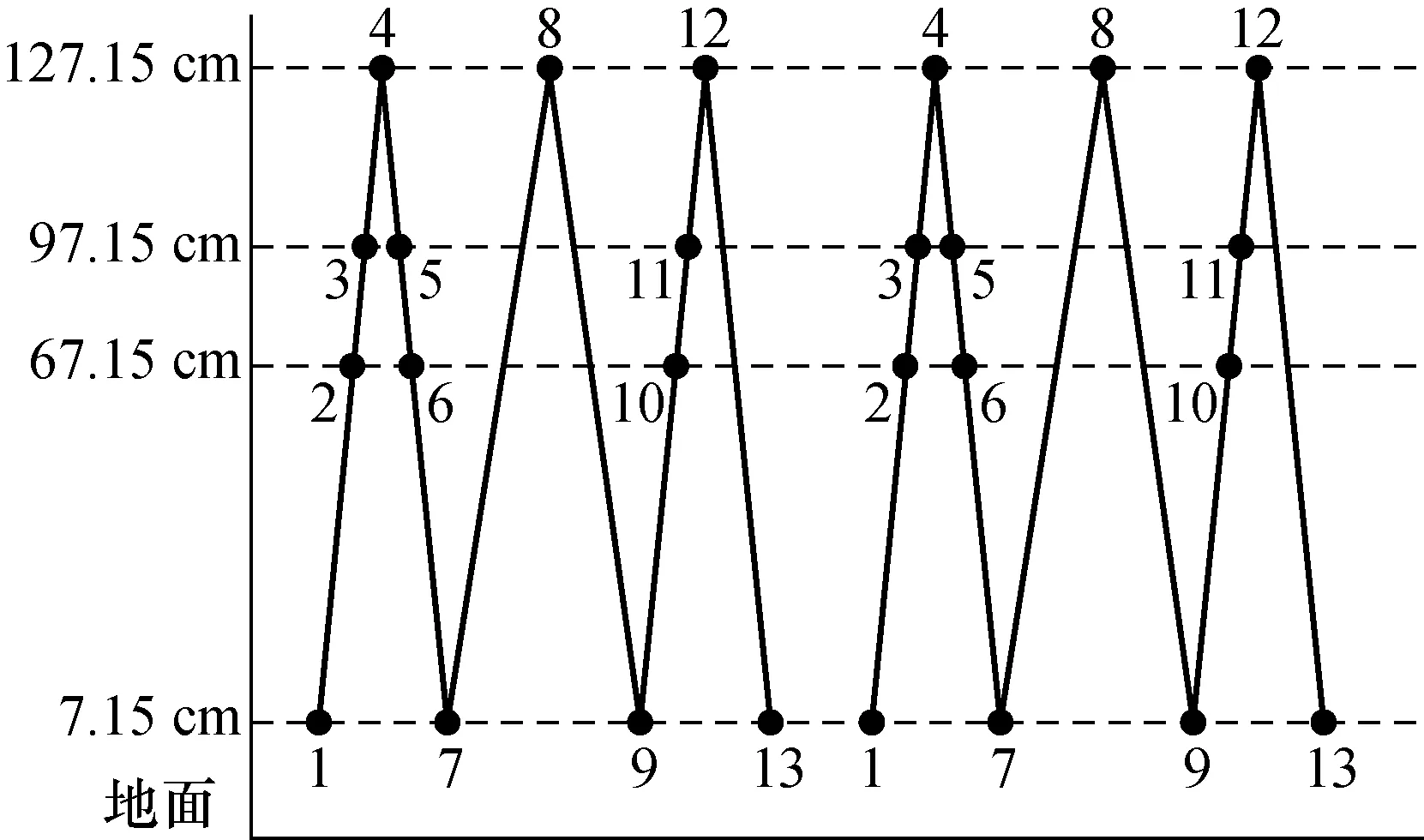
图2 相对重力仪Burris B095/B101点位梯度测量示意图Fig.2 Vertical gradient measurements at a station for Burris B095/B101

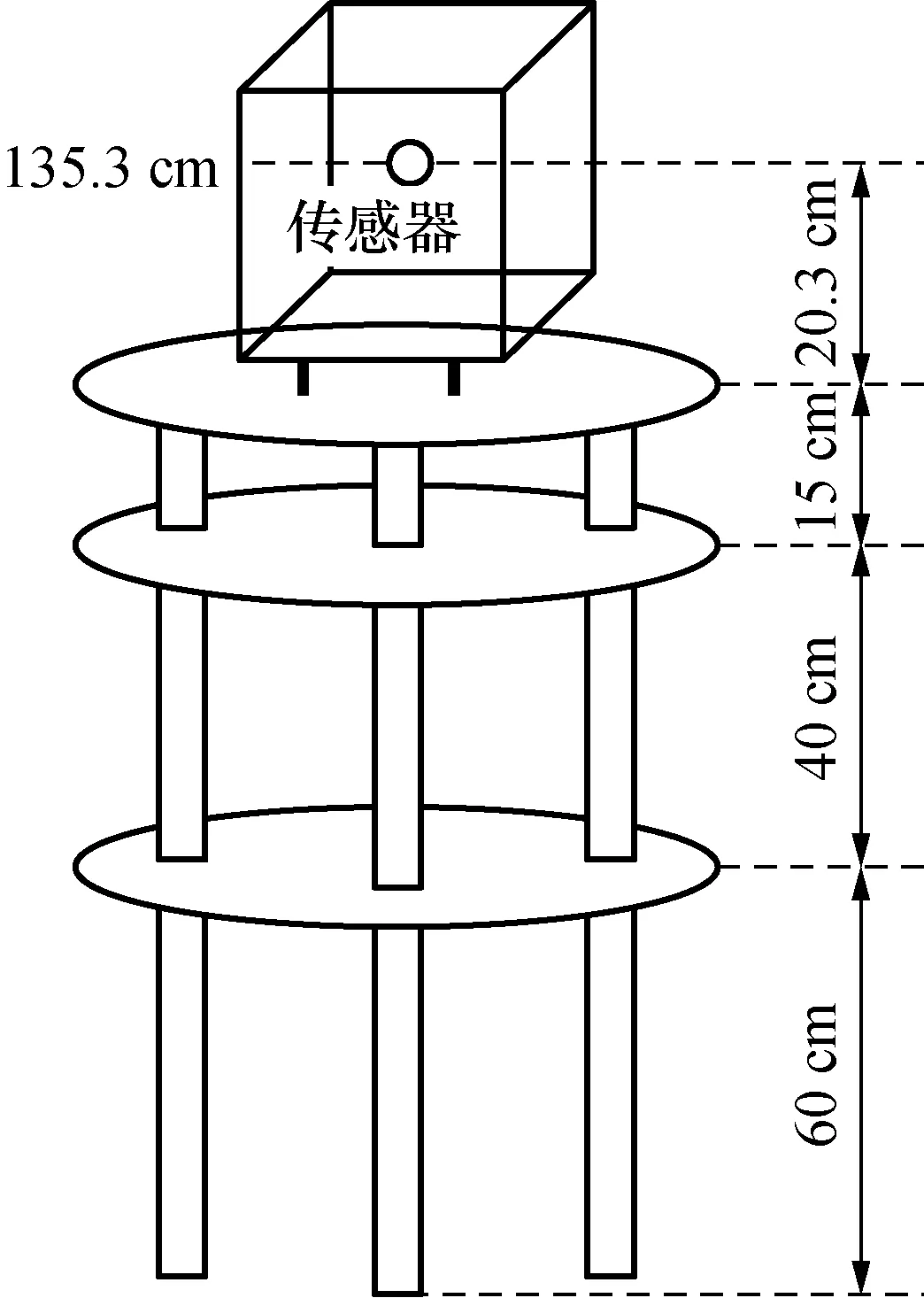
图3 相对重力仪CG-6 S032测量过程示意图Fig.3 Measurement set-up for a Scintrex CG6 gravimeter with combined tripods above a station

3 比对结果

3.1 相对重力测量数据处理及结果

此次比对的相对重力测量数据处理方法不同于以往比对,主导实验室基于最小二乘法提出求解矩阵方程的算法,可通过Excel或MATLAB实现。

对于重力垂直梯度求解,通常进行最小二乘拟合实现[3]。待求解的量为点位重力起算值和漂移常数,考虑到比对实验室的点位重力随高度的变化非线性,其二阶拟合模型如下:

g(h)=a+bh+ch2

(5)

式中:g(h)为点位重力值随高度的变化;h为高度。对于二次拟合求解梯度时,一般3个高度即可唯一地确定梯度拟合系数a,b,c。此次比对测量4个高度可以增加拟合点数和数据量从而提高二次拟合的精度。

梯度拟合结果如表1所示(其中σb和σc为拟合系数b,c的标准偏差,σbc为协方差)。

从表1可以看出,2号点位和5号点位的二次项系数c较小,这2个点位重力值随高度的变化趋于线性。其余点位重力值随高度的变化都具有较明显的非线性,其中9号点位的重力变化非线性最强,这也验证此次比对相对重力测量4个高度的必要性。

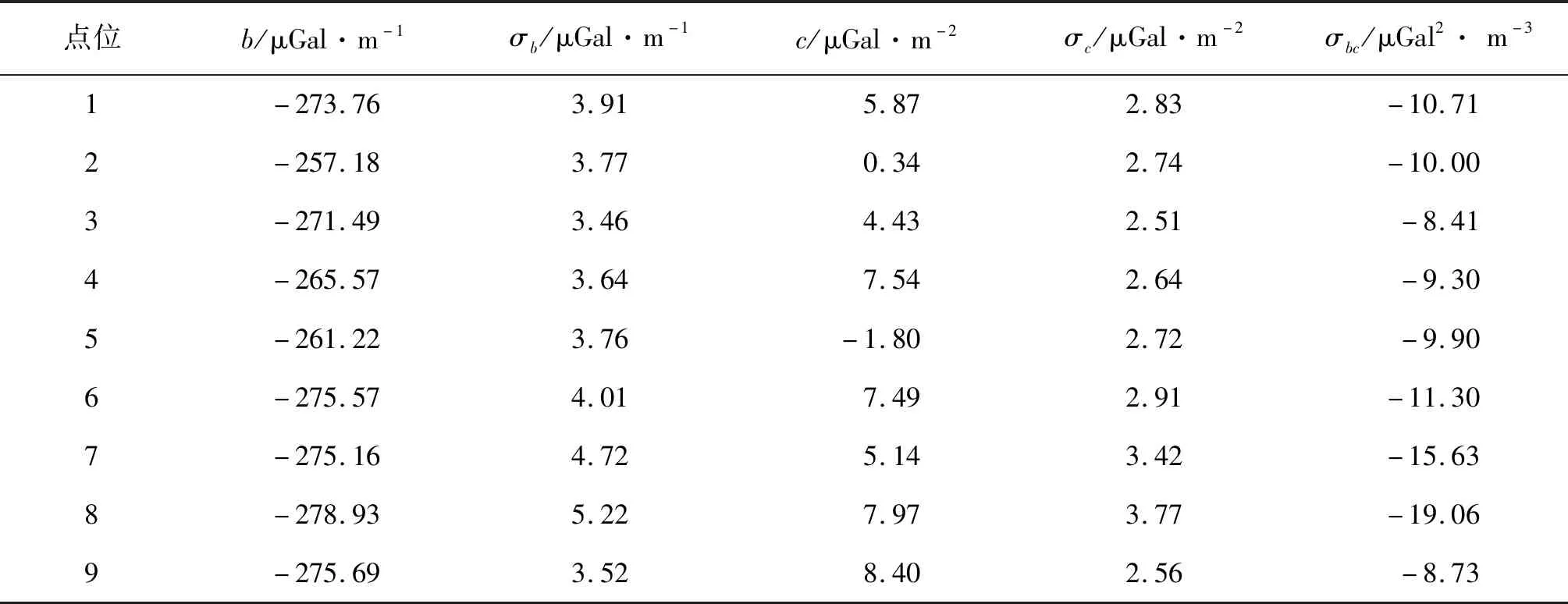
表1 点位重力垂直梯度拟合系数Tab.1 The parameters and associated uncertainties of the polynomial for the gradients.

注:1 μGal =10-8m/s2

3.2 相对重力测量不确定度

3.2.1 测量结果不确定度的A类评定

对于点位重力垂直梯度测量,每个点位由每台相对重力仪独立完成测量,每台相对重力仪完成2次循环(6次闭合)共计26次测量。每次测量每台相对重力仪得到一个读数,3台相对重力仪在一个点位最终得到78个读数,经数据预处理后通过最小二乘法解算出点位的梯度值。选取3号点位为例进行分析。h1和h2高度的重力段差δg为:

δg=g(h2)-g(h1)=b(h2-h1)+

(6)

相应的不确定度为:

(7)

由于相对重力仪传感器及三角架测量高度有限,此次梯度测量的高度范围为0.071 5～1.353 m。以最大归算高度1 m为例,假定h2=1.25 m(比对绝对重力仪归算统一高度),h1=0.25 m,从表1可以得知3号点位的σb、σc及σbc,代入式(7)计算可得不确定度为0.96 μGal/m,即3号点位不确定度的A类评定为0.96 μGal/m,其余点位的梯度测量不确定度可类似求解,基本实现了比对相对重力测量1 μGal/m的不确定度要求。

3.2.2 测量结果不确定度的B类评定

对于相对重力仪而言,参照以往比对经验[3]相对重力测量B类评定如表2所示。

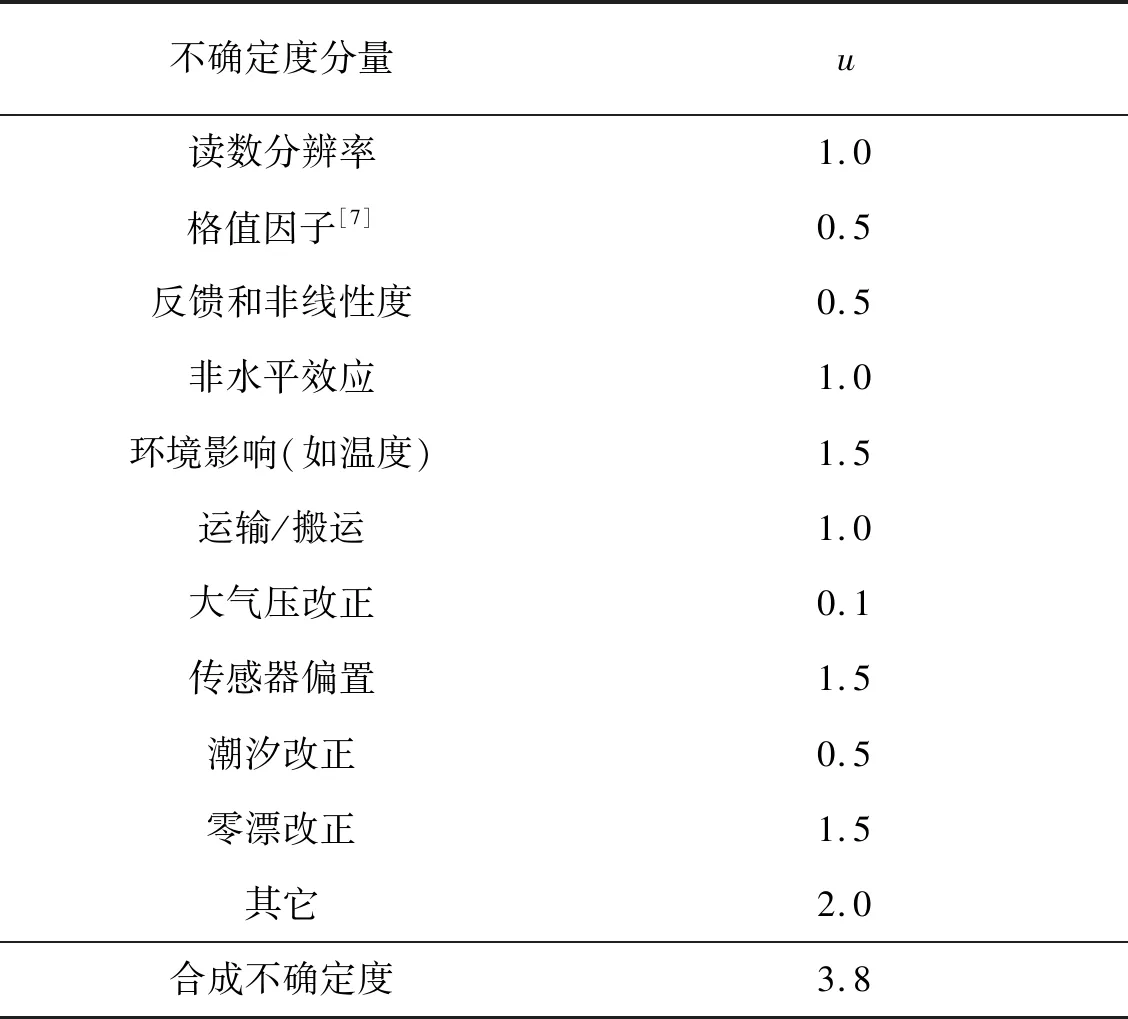
表2 相对重力测量结果不确定度的B类评定Tab.2 Type B evaluation of standard uncertainty of relative gravity measurements μGal

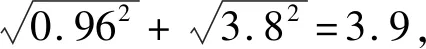
4 结 论

经过了1个多月的时间,完成了2017年第10届全球绝对重力仪关键比对。作为该领域30多年来首次移出欧洲的国际比对,本次比对取得了有效可靠的结果。本次比对表明:高精度的相对重力测量是保证比对结果准确可靠的主要因素之一,其中绝对重力值归算所带来的不确定度基本优于1 μGal,实现了预期微伽级的测量不确定度要求。对未来举办绝对重力仪国际比对完成了必要的技术积累,为绝对重力基准点提供有效连接,并最终建立起统一的重力垂直梯度测量规范来服务于绝对重力仪比对,确保了绝对重力仪国际关键比对点作为重力加速度量值的准确性。