Richardson-Lucy算法在模糊图像复原中的改进

张建国， 拓洋洋， 蒋瑞娇， 姚泰安， 王彦柱

(1.西安建筑科技大学 理学院，陕西 西安 710055； 2.西安建筑科技大学 信息与控制工程学院，陕西 西安 710055)

1 引 言

图像复原是利用光学成像系统在成像过程中的先验知识求出退化图像的原始图像近似值的过程。图像退化的原因很多,针对不同降质情况现已提出大量有效的复原算法，例如经典的维纳滤波、基于贝叶斯定理的Richardson-Lucy(R-L)算法以及小波域复原算法[1]。当噪声存在时经典逆滤波法复原效果不太理想，维纳滤波法尽管在某些程度上克服了逆滤波法的缺陷，但需要有关图像的先验知识；R-L作为图像复原迭代算法中的经典算法，虽然该算法复原效果较好,但它存在两个很难避免的缺陷:一是当图像的噪声增大时会出现噪声放大现象；其次是R-L迭代算法会消耗大量的时间且容易产生振铃效应[2]。

针对上述问题,本文提出一种嵌入式图像复原速率改进的设计方案，对系统采集到的图像使用 R-L算法结合二维小波变换复原图像，进而提高该嵌入式系统的实时性，使系统具有更快图像处理速率和更佳的处理效果[3]。

2 图像退化的数学模型

2.1 图像退化模型

连续图像的退化模型通常可以简化成图1所示的数学关系[4]。输入图像f(x,y)经过退化系统或模糊函数H(x,y)(在光学中称H(x,y)为点扩展函数)后产生的退化图像g(x,y)，公式为[4]：

g(x,y)=H[f(x,y)]

(1)

在考虑噪声影响时，退化图像可表示为：

g(x,y)=H[f(x,y)]+n(x,y)

(2)

图1 图像退化的数学模型Fig.1 Mathematical model of image degradation

由式(2)可知，退化图像是由光学系统退化后的图像和系统噪声叠加形成的模糊图像。假设H(x,y)和n(x,y)为已知量，那么退化模型的逆运算就是去模糊的过程，最终将f(x,y)的最佳估计值作为原图像的近似值。当求解逆运算时出现以下2种情况：2) 逆运算时最佳估计值无解时；2) 逆运算时存在多个解时，会出现图像复原病态性而产生不理想的结果。

连续图像f(x,y)可以表示为：

(3)

式中δ函数表示空间上的脉冲冲激函数。

将式(3)代入式(1)，可得：

(4)

式中h(x,y)为冲击响应函数。

在光学成像系统中，冲击则为一个光点，光学成像系统的响应却是扩散了的模糊光斑，因此又把h(x,y)叫做点扩展函数(FSF)。所以退化系统的输出响应g(x,y)就是f(x,y)与h(x,y)的卷积再加上噪声。在空域中图像的退化模型可表示为：

g(x,y)=f(x,y)⊗h(x,y)+n(x,y)

(5)

数字图像处理的为离散图像，所以只要把数字图像离散化成大小为X×Y矩阵即可解决。对式(5)进行离散化，假设输入图像f(x,y)大小为E×F，点扩展函数h(x,y)均匀采样为G×K大小。为了避免交叠误差的情况出现，用添零延拓法将它们扩展成M=E+G-1和N=F+K-1个元素的周期函数[5]。

(6)

(7)

则输出降质的数字图像为：

(8)

式中：x=0，1，2，…，M-1；y=0，1，2，…，N-1。因此二维离散退化模型的矩阵形式为：

g=Hf

(9)

考虑噪声时，则数字图像退化模型为：

g=Hf+n

(10)

由式(10)可知，已知g(x,y)、h(x,y)和n(x,y)时可得到原图像的近似值[6]。但实际工作中并非线性空间不变模型，所以此基础之上进行改进才能更好地解决实际问题并具有较高的科研价值。

2.2 离散小波变换理论

离散小波变换(discrete wavelet transform，DWT)使用连续的低、高通滤波器结合采样的方法实现[7]。

一维离散信号的小波变换过程为，信号S通过高通、低通滤波器后分别进行一次下采样，S被分解成高频分量y1和低频分量x1；继续x1和y1进行上述步骤处理可得到第二层小波变换；以此类推可得到所需的分辨率。一维离散信号的两级小波变换可用图2的形式表示，图2中，S代表输入的一维离散信号；H和L分别代表高频和低频滤波器；↓代表下采样操作。

图2 一维离散信号的两级小波变换Fig.2 Two level wavelet transform for one dimensional discrete signals

将上述过程扩展到二维图像A时，设A的大小为E×F，使用高通滤波器H和低通滤波器L对A进行滤波和下采样，产生2幅大小为(E/2)×F图像AH和AL；继续使用H和L对AH和AL进行滤波和下采样，生成AHH，AHL，ALH和ALL4副图像。其中ALH为A的水平分量，AHL为A的垂直分量，AHH为A的对角分量，ALL为A的低频分量的近似值，见图3所示。

图3 二维图像的小波变换Fig.3 Wavelet transform of 2-D image

3 R-L图像复原算法及改进

3.1 R-L算法

R-L算法是Richardson和Lucy提出的，该算法是以贝叶斯定理和条件概率为基础实现的[8]。R-L算法源于贝叶斯公式：

(11)

式中：P(X|Y)表示Y事件发生的条件下X事件发生的概率;P(Y)、P(X)分别是Y、X事件发生的概率。由于：

(12)

将式(11)代入式(12)，可得：

(13)

假设X为原始图像，Y为退化图像，则P(X)为原图像的灰度分布f(x,y)，P(Y)为退化图像的分布g(x,y)，P(Y,X)是以点(x,y)为中心的点扩散函数h(x,y)。把这些量代入式(13)，可得卷积形式为：

(14)

式中：k是迭代次数，一般选择初始条件为f0(x,y)=g(x,y)进行迭代，当k不断增大时,fk+1(x,y)收敛于f(x,y),进而可求得图像的近似值。式(14)即为R-L算法的迭代公式[5，6]。

3.2 R-L算法改进

R-L算法为图像复原迭代算法中的经典算法，小波域复原算法借助小波的多分辨特性，在变换域的高低频部分采用不同的复原算法可实现图像复原。针对R-L算法和小波域复原算法各自的特点，本文提出R-L算法和二维离散小波变换[9,10]结合的图像复原的复合算法,解决R-L算法的噪声放大和耗时性[11]两个问题，提高R-L算法效率的同时且能很好地抑制图像噪声放大的问题[12]。

具体改进过程为，用二维小波对目标图像进行2次分解产生多副细节图像，根据每副图像所含原始图像细节信息的比例大小进行R-L迭代。对于高频的图像细节部分使用少次R-L算法迭代；对于低频图像部分使用R-L算法多次迭代；对大尺寸图像用更少的R-L算法迭代可以大幅分缩减计算时间。算法任务的设计流程见图4所示，当传感器采集到图像后，触发处理去模糊任务的同步信号进而解锁执行任务。

图4 算法任务流程图Fig.4 Algorithm flow chart

设定任务中等待的同步信号量，当需要执行该任务时就会释放同步信号量，此刻若去模糊复合算法任务处在等待信号量的状态并且没有更高优先级的任务时，会被执行且不会被次优先级的任务打断。进程被解锁后，需要从环形队列中读取数据到去模糊复合算法的数组中来确保此次计算的完整。若出现其它中断事件后，CPU被切换到相应的事件中时保证该任务继续将数据送入环形队列中，但此时还处于中断服务状态，故普通的任务无法被切换到执行状态，但原始数据可能遭到破坏，故应当在计算开始之前，临时关闭中断，当完成数据拷贝后恢复。使用二维数组存储图像数据时，为了降低算法实现的复杂度，采用逐行读取首尾相连转换成一维信号。

4 实验与结果分析

4.1 实验设计

将改进后的算法移植到嵌入式系统中验证是否达到预期的效果，该嵌入式系统搭载EXYNOS4412四核处理器，集成4个1.5 GHz频率的处理器核心及1个GPU图形处理核心。在该芯片上搭建外接摄像头的接口电路及供电模块、存储模块等核心电路接口[13]。图像采集传感器模块使用CMOS摄像头，功耗低、体积小，支持多种输出格式和各种尺寸；图像存储模块采用8 G大小的普通SD储存卡进行储存。该系统的主要功能为图像信息采集、存储和图像复原处理。

设计多线程多任务调度的管理方案，实现底层硬件的中断管理和任务调度、内存管理及编写各模块的驱动程序。通过Linux操作系统调度采集模块并分配内存，每当一次图像采集完成都会将图像数据存储到FIFO(先进先出)帧存储器中，再通过应用程序将存储器的图像数据写进Flash Memory内[14]；接着操作系统调度改进后的复合算法对采集到的图像进行处理，获得清晰图像并将图像保存在储存模块中；最后读取目标图像进行结果分析和质量评估。

4.2 实验结果分析及评价

4.2.1 图像质量评价方法

本文主要使用均方误差(MSE)、均方根误差(RMSE)和峰值信噪比(PSNR)这3参数值对去模

糊后的图像质量的性能进行评价。

(15)

(16)

(17)

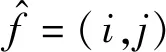
4.2.2 图像质量评价结果

图5为4组不同场景中采集的图像，每组实验分别使用反卷积法、R-L和本文算法3种方法对图像进行复原处理，顺序分别是实验采集图像的灰度图像、逆反卷积法复原图像、L-R法复原图像，最后一幅是本文算法复原的图像。为体现客观性，4组实验使用格式为jpg分辨率各不相同的图片。

复原后图像的MSE、RMSE和PSNR结果列于表1。由表中数据可知：逆反卷积法不能提供足够的PSNR值，但本文方法给出了良好的PSNR值；本文方法具有图像去模糊的较好性能，同时提高了图像的清晰度和视觉质量。

4.2.3 算法耗时性对比

计算时间是评价某种算法的标准之一，对3种算法的计算时间进行对比，见表2所示。需要指出的是，因为原始R-L算法存在一个迭代的过程，其计算平均时间随迭代次数的增加而增大。与此相反，当使用本文设计的小波变换结合R-L的复合算法时，由于在这个大比例部分使用较小的迭代次数，使得计算时间大幅减少。因此在计算最佳的复原滤波器时，它规避了大量的时间消耗过程。

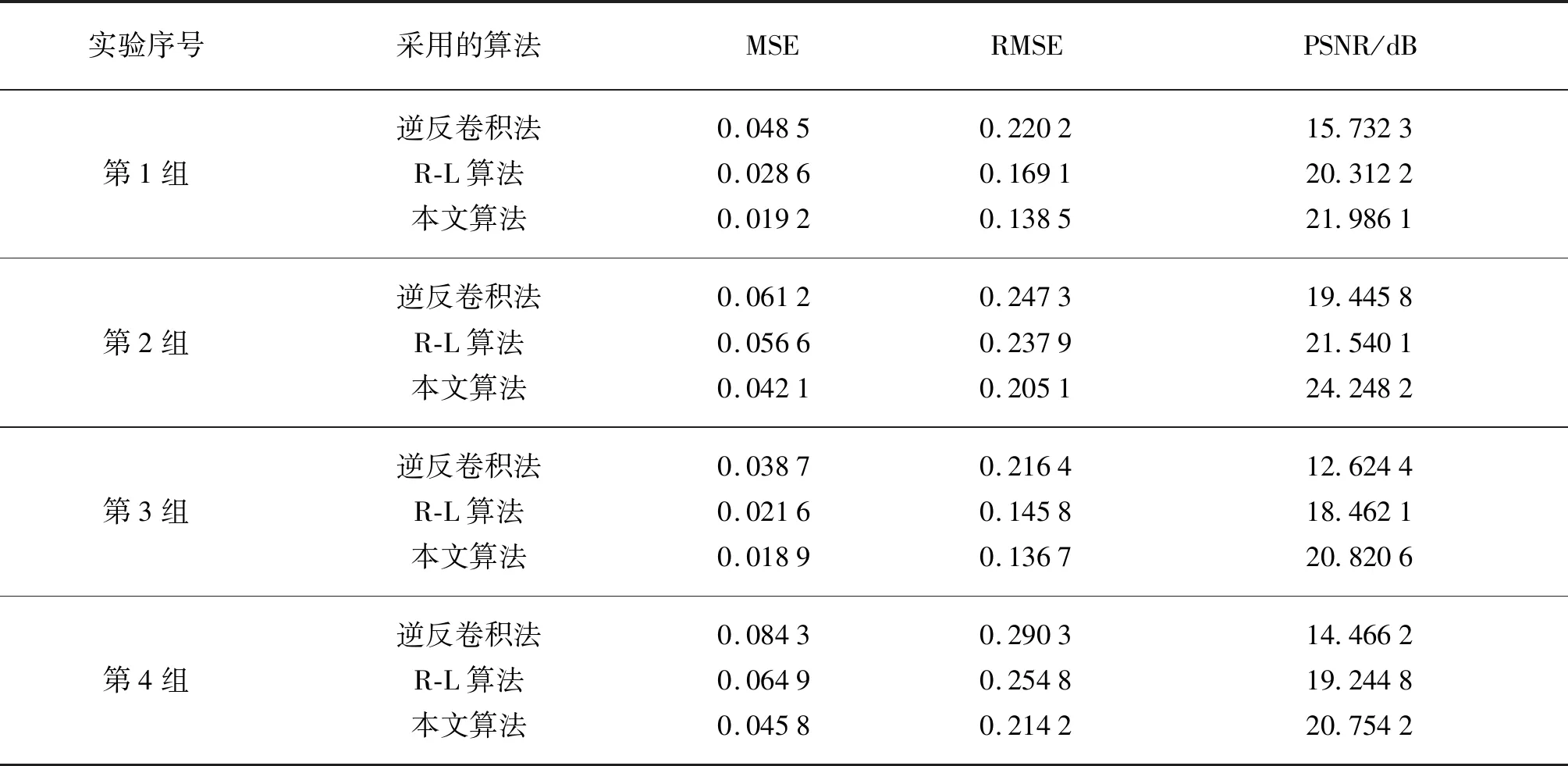
表1 各算法结果参数对比Tab.1 Comparison of algorithm result parameters

图5 4组实验结果对比图Fig.5 Comparison of 4 sets of experimental results

表2 各算法计算时间对比Tab.2 Comparison of computation time of each algorithm

5 总 结

(1) 设计了采集与处理图像功能的嵌入式系统，结合嵌入式系统的要求和处理器的性能特点，选择了Cortex-A9内核的EXYNOS4412芯片，移植了Linux 3.5操作系统并设计了系统总体硬件电路。

(2) 设计了图像采集模块的程序设计和存储模块的程序设计。针对图像复原的经典算法逆卷积算法、R-L算法和R-L算法结合小波变换对图像进行复原处理和分析，最终对基于R-L算法为基础的图像复原算法进行改进。

(3) 实验数据对比证明，改进后的复合算法在降低计算时间的同时图像复原的效果也有很大程度的提升。