几何重心法亚像素提取算法研究
2020-04-11徐从裕高雨婷杨雅茹胡宗久
徐从裕, 高雨婷, 徐 俊, 杨雅茹, 胡宗久
(合肥工业大学 仪器科学与光电工程学院,安徽 合肥 230009)
1 引 言
小于2.00 r/min的转速一般称之为超低转速。超低转速的传统测量方法主要是采用光栅[1]、光电编码器[2]或激光多普勒技术等光学方法进行检测;此外,通过涡流传感器[3]或旋转磁场[4]也可进行转速测量;文献[5]采用固定在隔振基础上的测量长杆上的电感测头进行检测;文献[6]提出了一种基于旋转变压器的多周期后向差分的转速计算方法。
随着影像设备性能的提高和价格的降低,影像技术的应用越来越多,将其应用于测速仪器是当前的一种发展方向[7],如:利用影像技术对获取的目标图像进行二值化、霍夫变换、特征量提取等处理可得到被测物的转速[8~10]等。
为了提高影像技术在超低转速测量的实时性和扩展超低转速下限值,本文提出一种基于显微图像法的几何重心法的快速亚像素提取算法,以解决目前超低转速在线测量存在的实时性不足问题和超低转速下极限值受限问题等。
2 显微图像法的超低转速测量原理
超低转速测量系统是由显微镜头、计算机和图像分析软件组成,如图1所示。显微镜头放置在被测转台边缘,利用显微镜头视场小的特点,将转动测量转化为平动测量,即定时读取显微镜头的显微图像,对相邻的两幅图像的位移值即弧长值进行测量,获取到的弧长值代入到转速测量函数中,就可解算出转台的转速值。
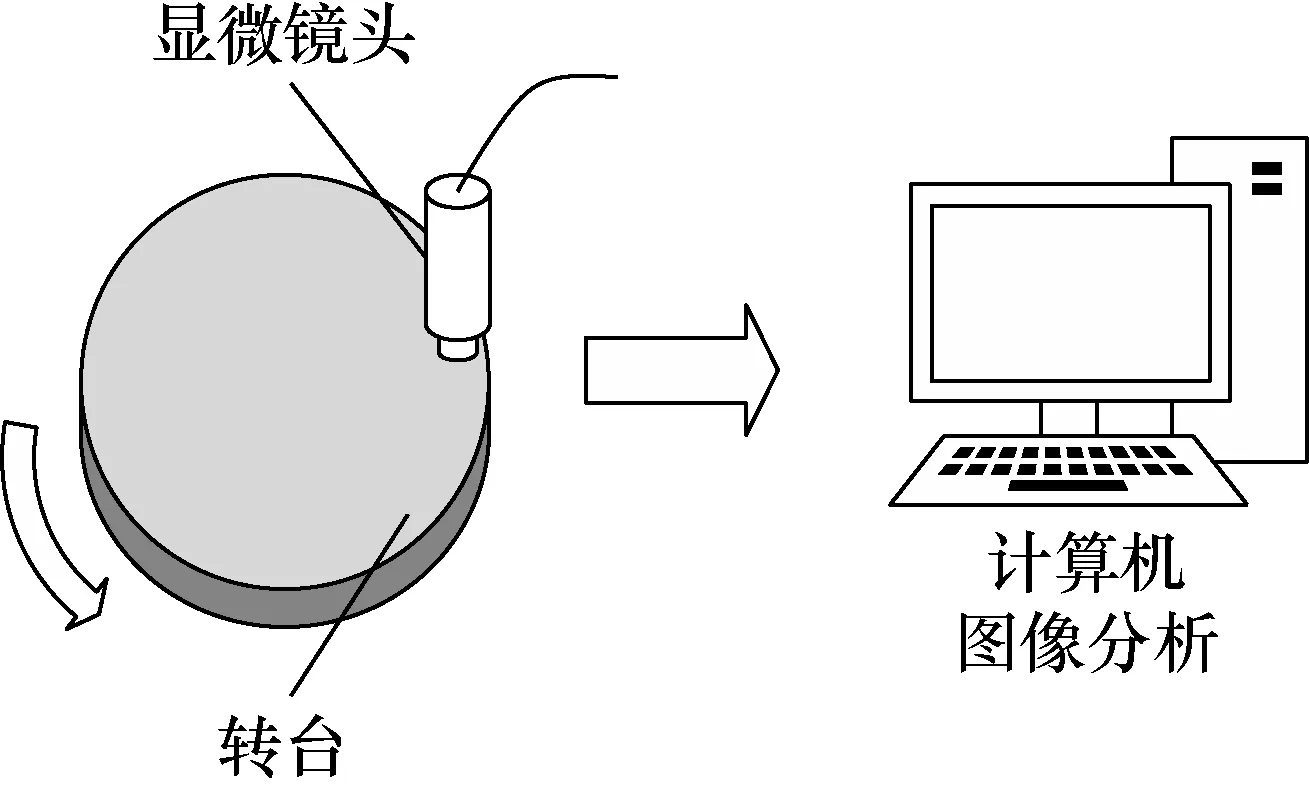
图1 显微图像法的转速测量系统示意图Fig.1 Rotating speed measurement system based on microscopic image method
显微镜头全域的视场范围为:(1.0~1.5 mm)×(1.0~1.5 mm),显微图像区域在转台的位置如图2所示。
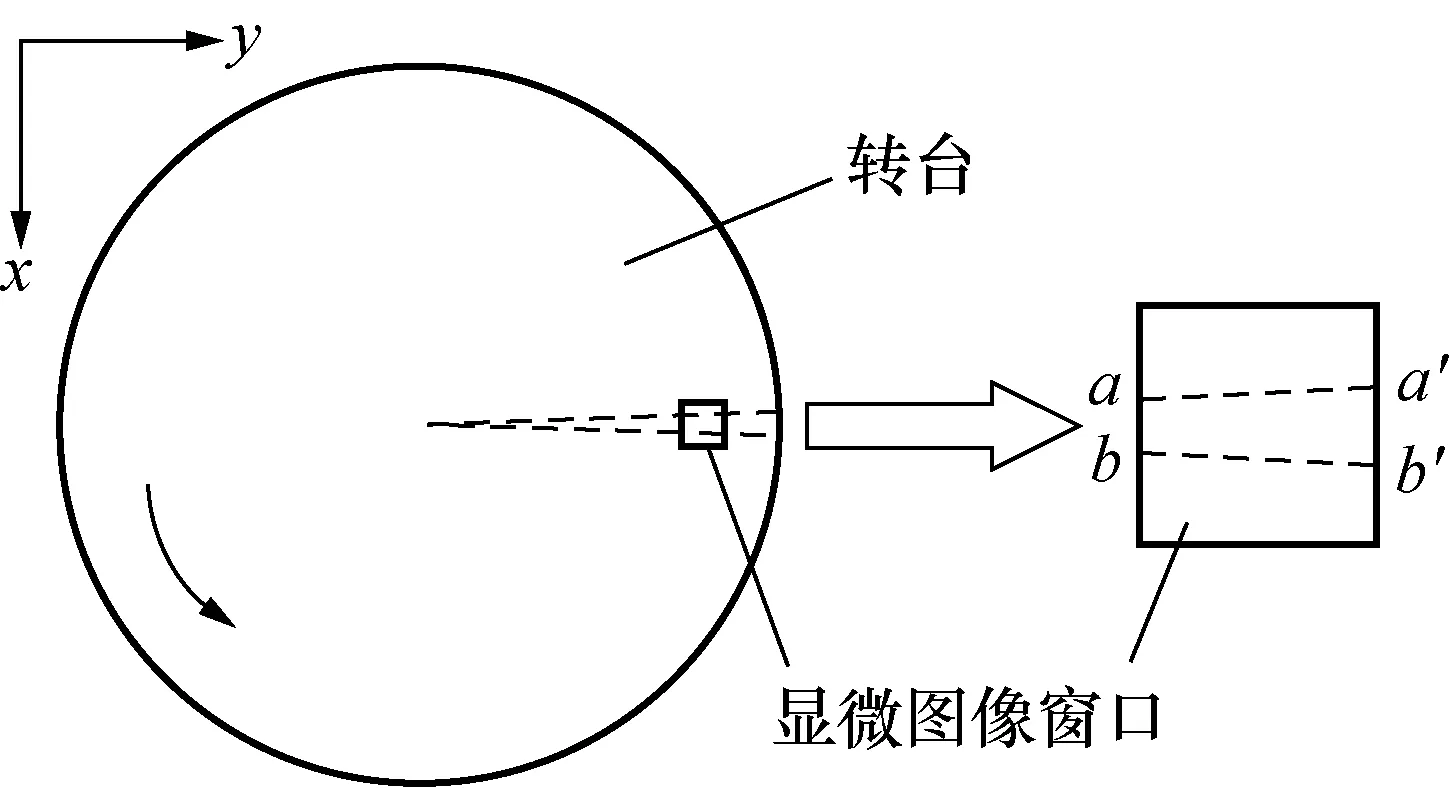
图2 显微图像区域选取Fig.2 Selection of microscopic image regions
由于采用超低转速测量,定时获取到的两幅散斑图像,其位移ab值与a′b′值基本相同,折算成像素值,两者之差小于0.05 pixel,因此可以将转台的转动测量看成是x方向的平动测量。
由超低转速测量原理可知,超低转速测量已经转化为微位移测量,而微位移测量的关键,取决于图像法中亚像素提取算法的实时性和亚像素提取的分辨率。
3 几何重心法的亚像素算法
本文只介绍曲面拟合法、梯度法和所述的几何重心法的亚像素提取算法。
3.1 曲面拟合算法
该算法首先利用整像素相关法计算得到目标图像中相关系数最大的点(x′,y′),通过此极值点及其周围的几个点组成相关系数矩阵,对此系数矩阵进行拟合为连续曲面,寻找该曲面的极值位置可得到目标图像的亚像素位移,一般均采用二元二次多项式来拟合相关函数曲面[11],选取拟合窗口大小为 3×3像素。
二元二次曲面拟合函数为
(1)
式中a0~a5为6个待定系数。
则二元二次拟合曲面极值点的亚像素值为
(2)
3.2 梯度算法
当物体做微小位移时可看成做近似刚体运动,且位移前后同一点的灰度保持不变[12]。令f(x,y),g(x′,y′)分别表示位移前、后的子区图像灰度值,则有:
f(x,y)=g(x′,y′)=g(x+u+Δx,y+v+Δy)
(3)
式中:u,v分别为目标图像相对于参考图像的整像素位移;Δx、Δy分别为与整像素位移对应的亚像素值。
通过一阶泰勒级数展开,以及Barron算子的引用,得到Δx和Δy:
(4)
式中:gx,gy为灰度的一阶梯度;f,g分别为位移前的灰度值和位移后相应点的灰度值。
3.3 几何重心法
几何重心法的核心是在整像素提取的基础上,在3×3的像素范围内,分别计算参考像素灰度值与提取的整像素灰度之差的指数值,在获取的3点指数值上,利用几何重心法提取出亚像素值。
几何重心法的亚像素提取算法,是几何法和重心法的混合算法。
图3为整像素u、v附近的3×3像素矩阵图。
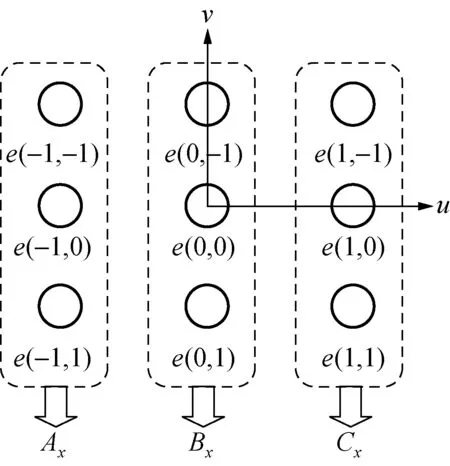
图3 3×3像素矩阵图Fig.3 3×3 pixel matrix drawing
图3中的各个参数的含义如下:
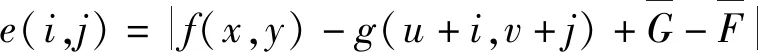
(5)
(6)
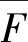
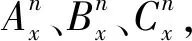
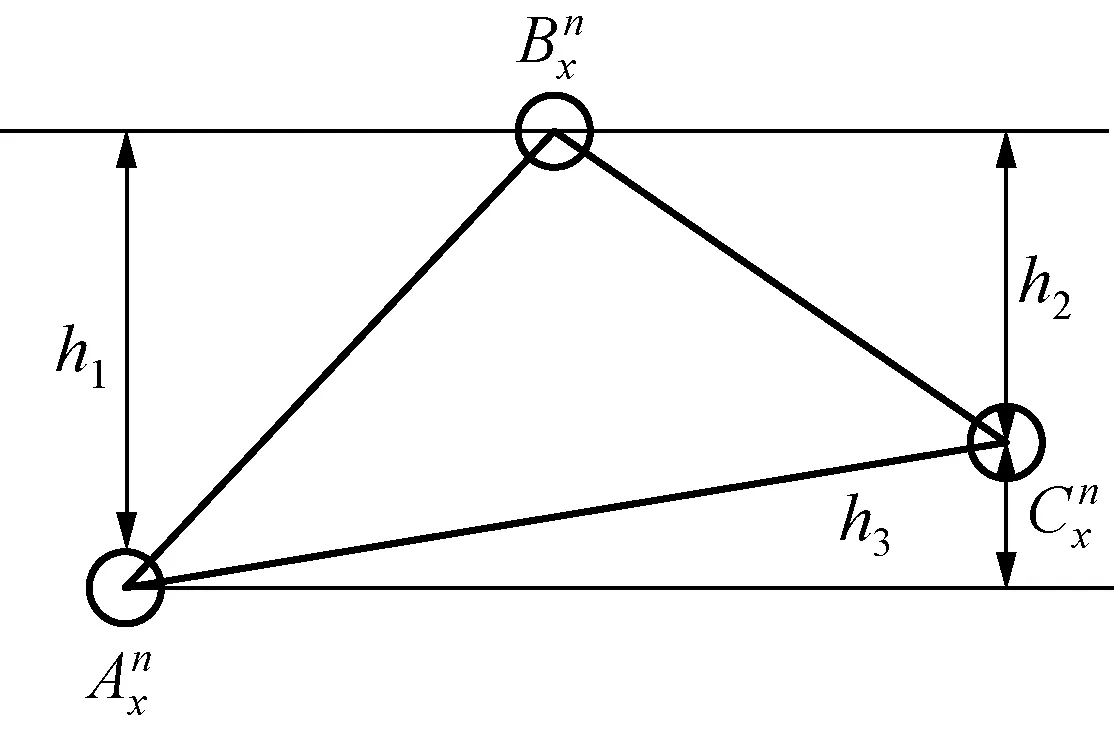
图4 几何法差值Fig.4 Differences of geometric method
则几何重心法的算法定义为
Δx=h3/(h1+h2+h3)
(7)
式中:Δx即为x方向上的亚像素值;h1、h2、h3由式(8)求出。
(8)
同理,如果沿着图3的u方向进行选取,按照上面步骤,可以得到y方向的亚像素值Δy。在下面的讨论中,根据超低转速的测量要求,只需考虑x方向的亚像素值Δx的提取问题。
4 实验结果及分析
4.1 实验装置
实验装置实物照片如图5所示。通过光栅基准平台的微纳米驱动,对图像的像素提取值、标准差和线性度进行验证。微纳米驱动平台每驱动10 μm位移抓取一幅图像,共抓取5组图像,每组图像为10幅,每幅图像之间的位移之差小于100 nm。

图5 实验装置实物图Fig.5 Physical diagram of experimental equipment
4.2 散斑图
图6和图7为光栅基准平台同一位置、不同时刻抓拍的散斑图,及其散斑图上位于中心线上的灰度曲线图。
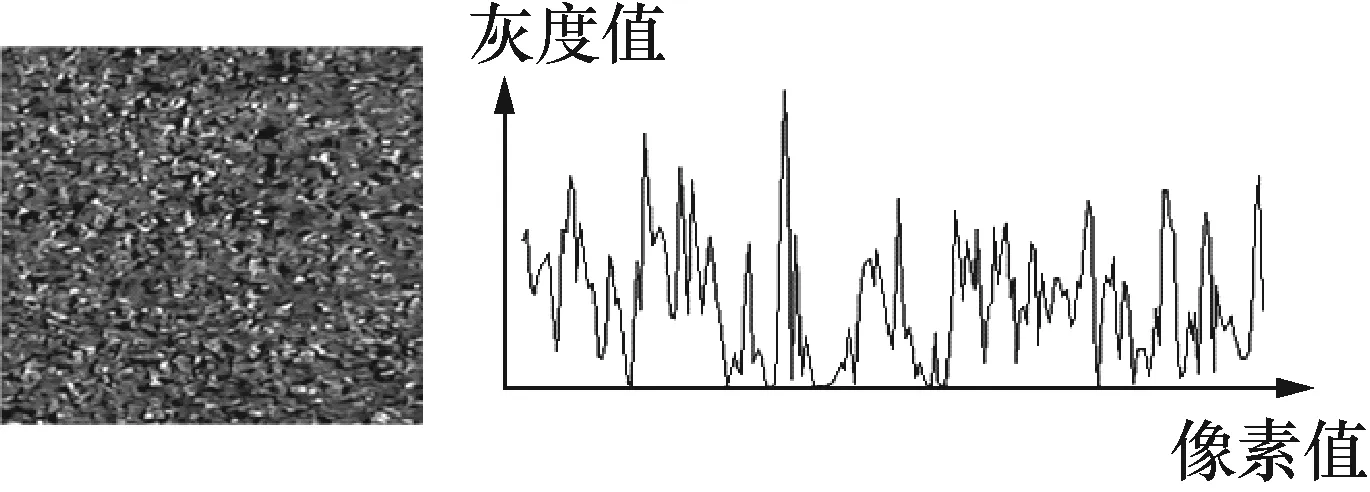
图6 时刻t0的散斑图及灰度曲线图Fig.6 Speckle pattern and grey scale curve at time t0
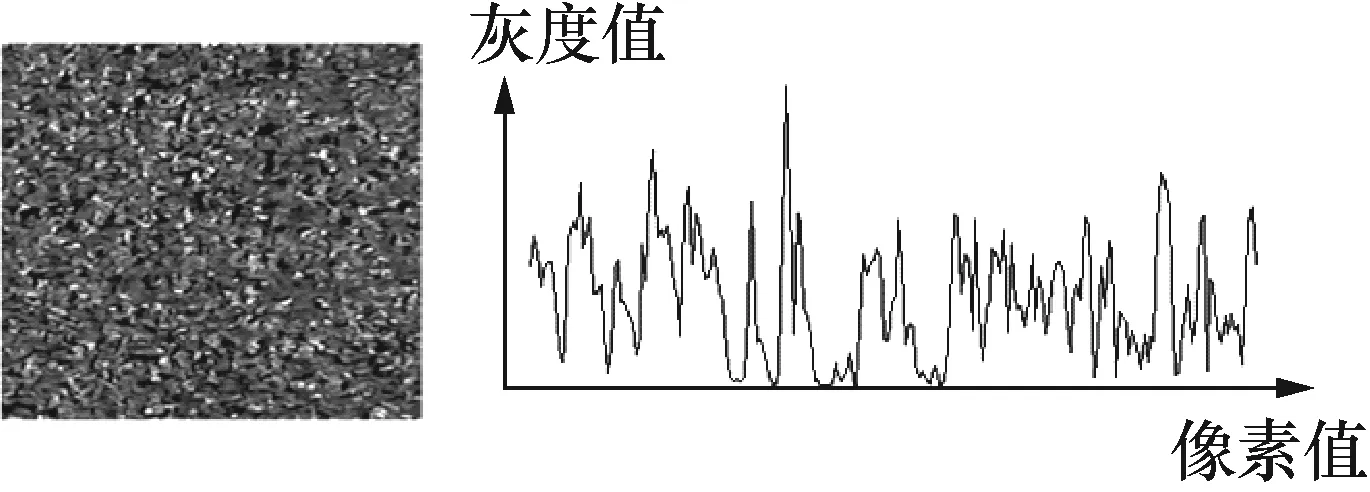
图7 时刻t1的散斑图及灰度曲线图Fig.7 Speckle pattern and grey scale curve at time t1
由图6和图7可以看出,在实际抓拍图像的时候,由于显微摄像头的图像干扰存在,不同时刻抓拍到的散斑图,都会有随机的图像干扰存在,进而导致同一图像位置、不同时刻抓拍的散斑图的灰度值发生变化。为解决随机图像干扰对亚像素提取的影响,一般都要在散斑图上的相关区域内进行N次的亚像素计算,然后再取N次的平均值作为最终的亚像素提取值。在下面的3种亚像素提取算法中,亚像素提取值均采用平均值。
4.3 计算结果对比
表1、2、3分别为曲面拟合法、梯度法和几何重心法在图像n与图像n+1之间提取的正向与反向像素值;表4、5、6分别为上述不同算法提取的正向与反向像素值的差值和标准差。其中,几何重心法相比较曲面拟合法和梯度法,其亚像素提取的标准差为最小。
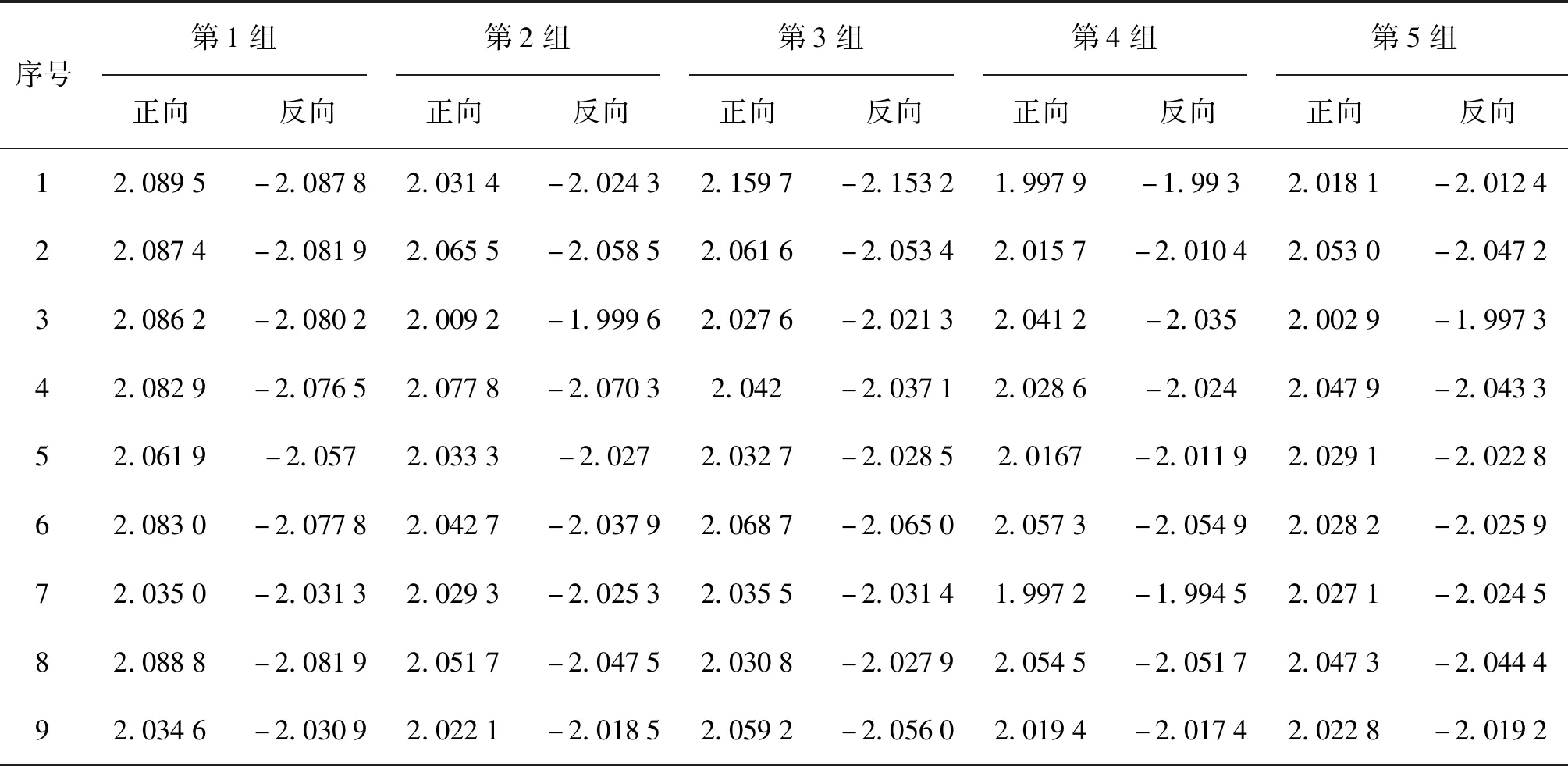
表1 曲面拟合法:图像n与图像n+1之间正反像素值Tab.1 The curved surface fitting method—positive and negative pixel values between image n and n+1 pixel
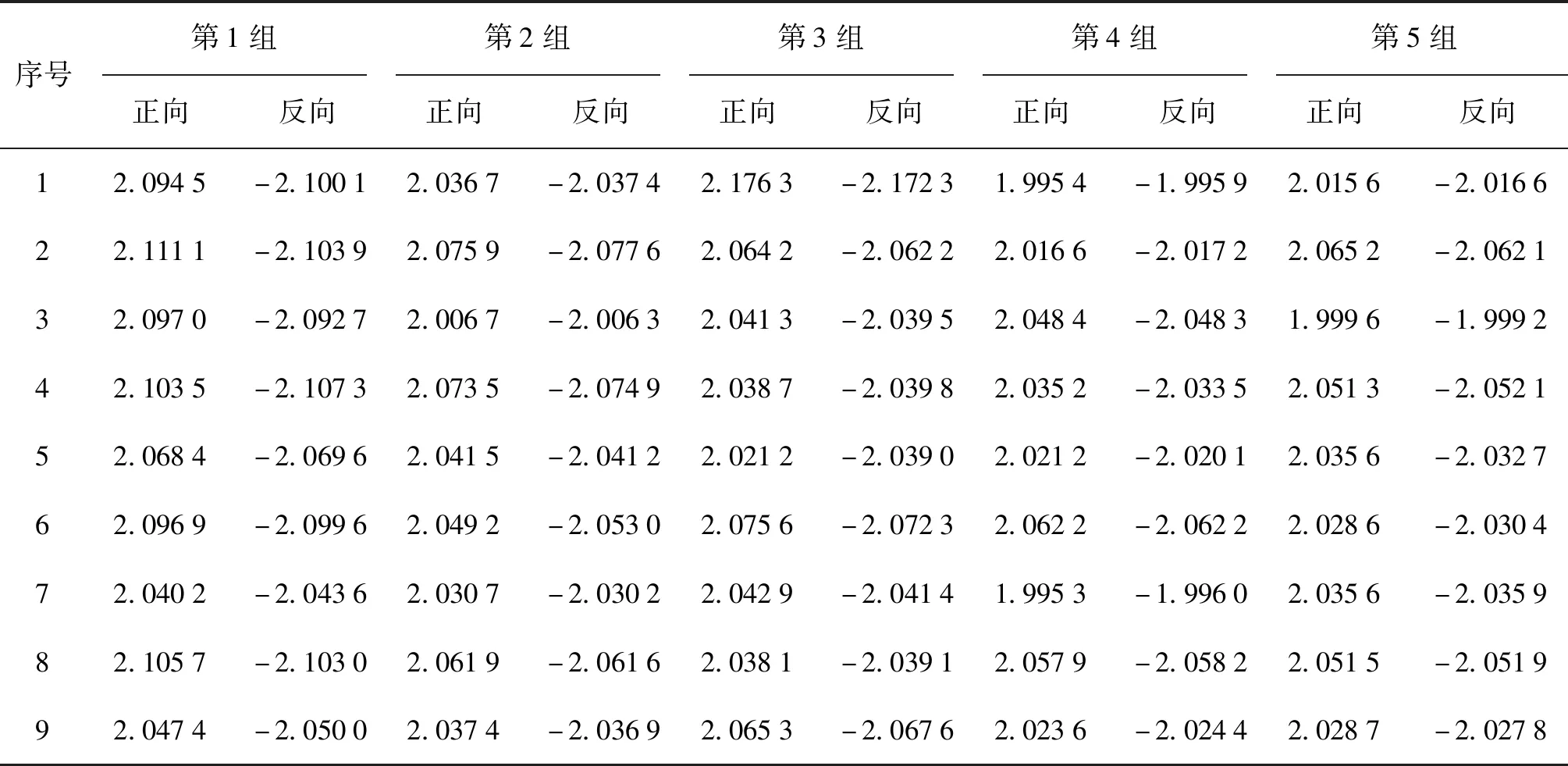
表2 梯度法:图像n与图像n+1之间正反像素值Tab.2 The gradient method—positive and negative pixel values between imagen and n+1 pixel
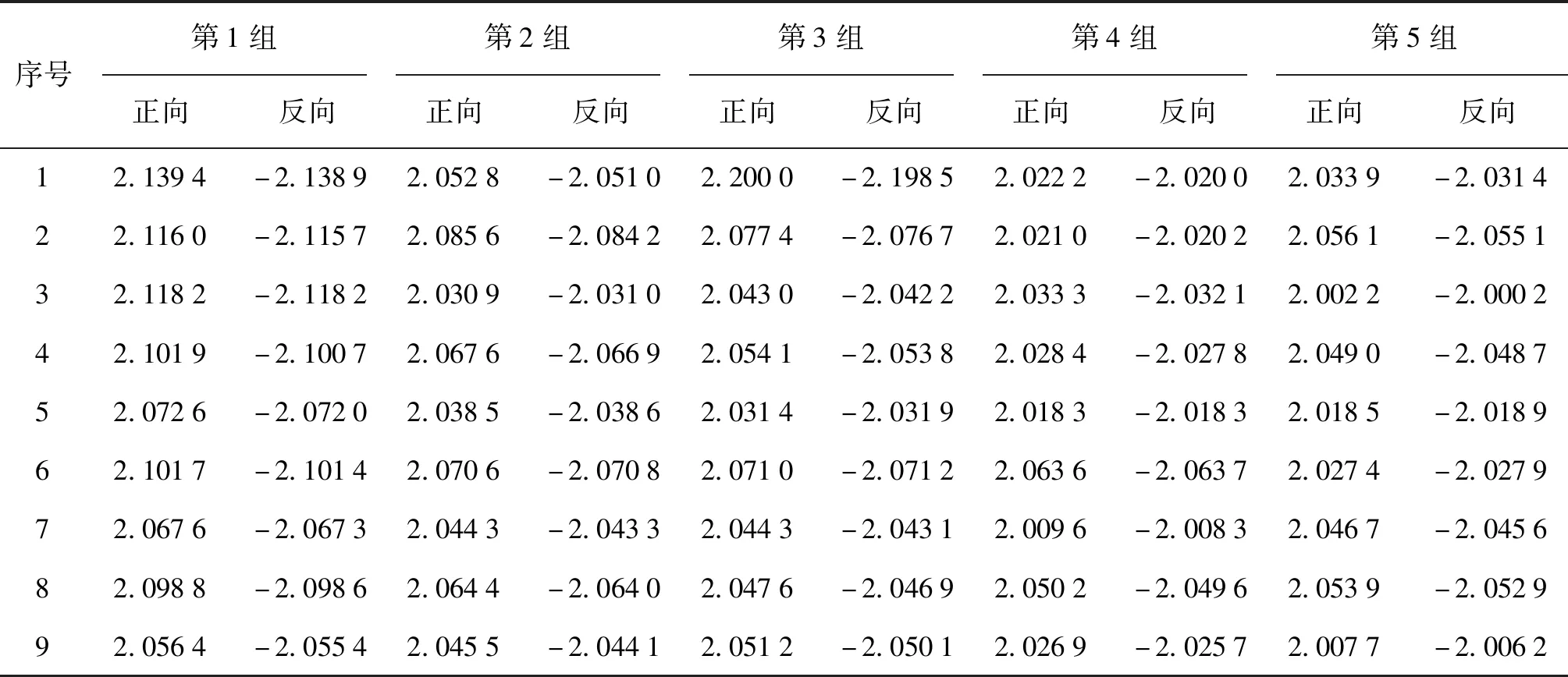
表3 几何重心法:图像n与图像n+1之间正反像素值Tab.3 The geometric center of gravity method—positive and negative pixel value between image n and n+1 pixel
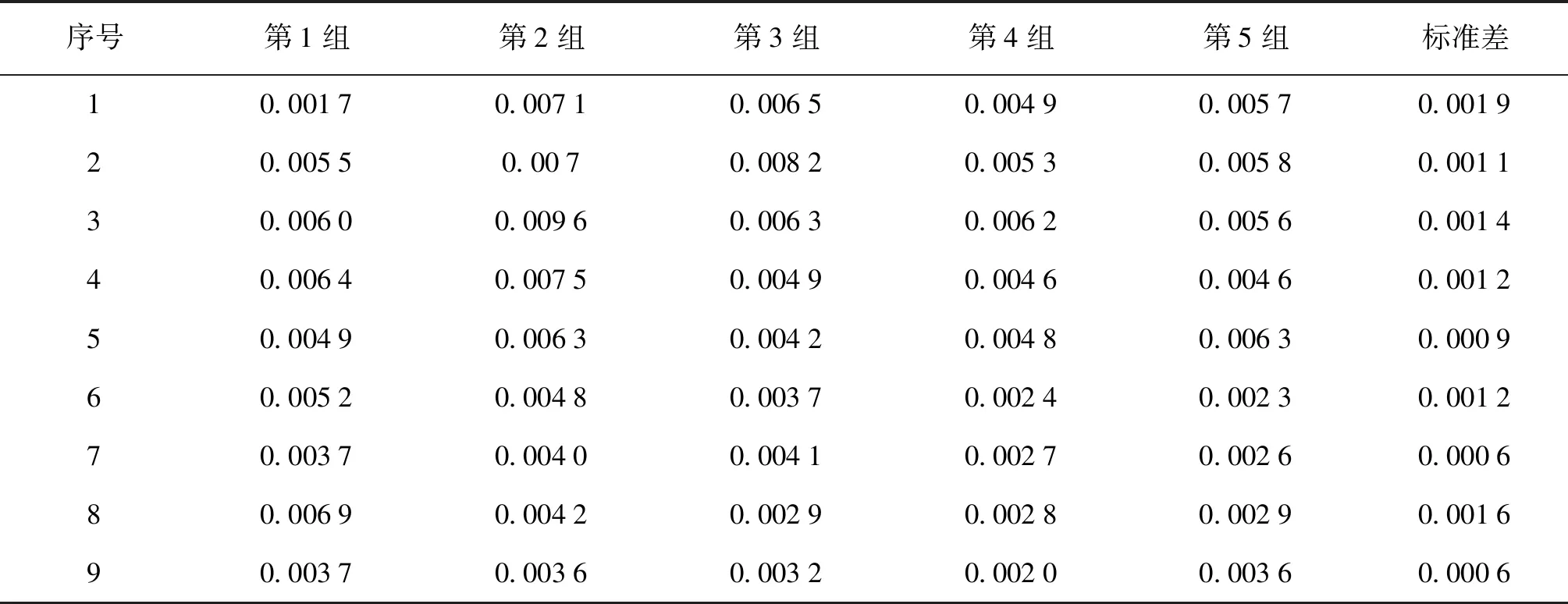
表4 曲面拟合法:正反像素差值和标准差Tab.4 The curved surface fitting method—positive and negative pixel differences and standard deviation pixel
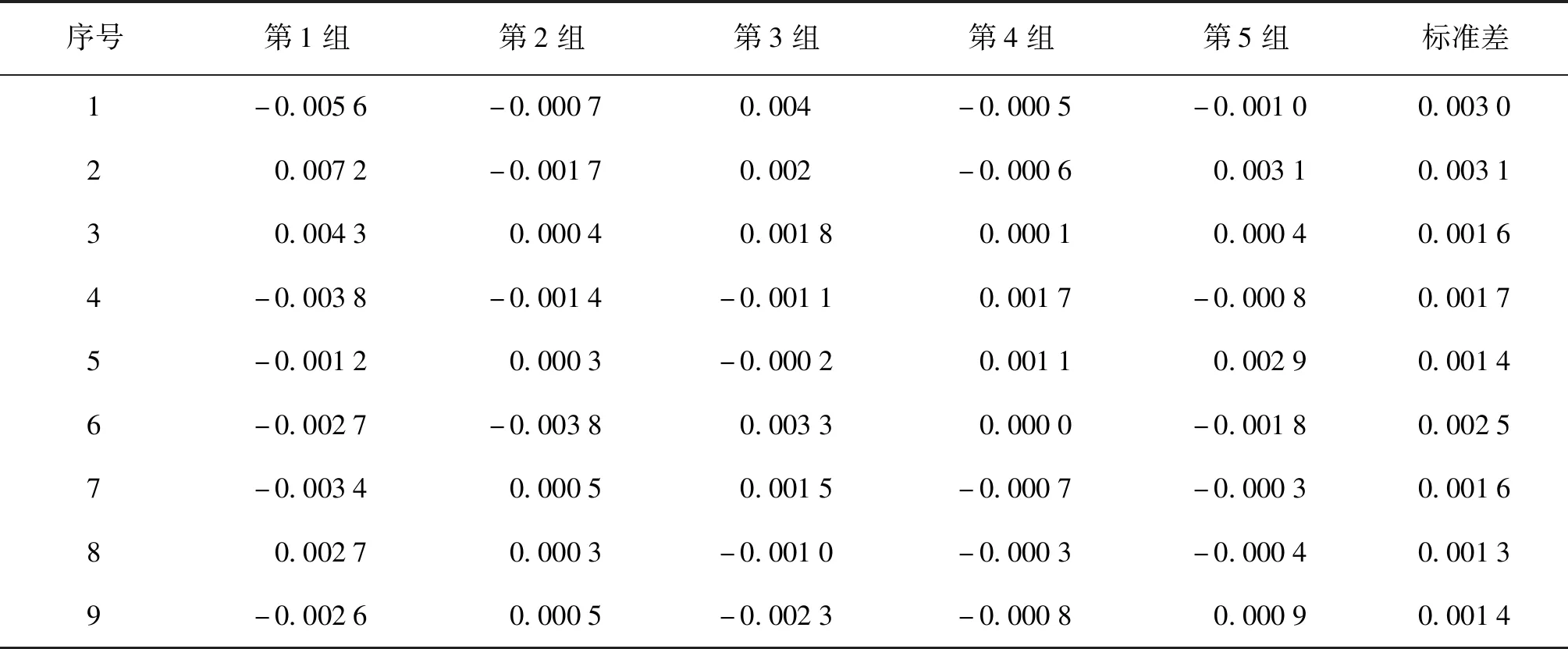
表5 梯度法:正反像素差值和标准差Tab.5 The gradient method—positive and negative pixel differences and standard deviation pixel
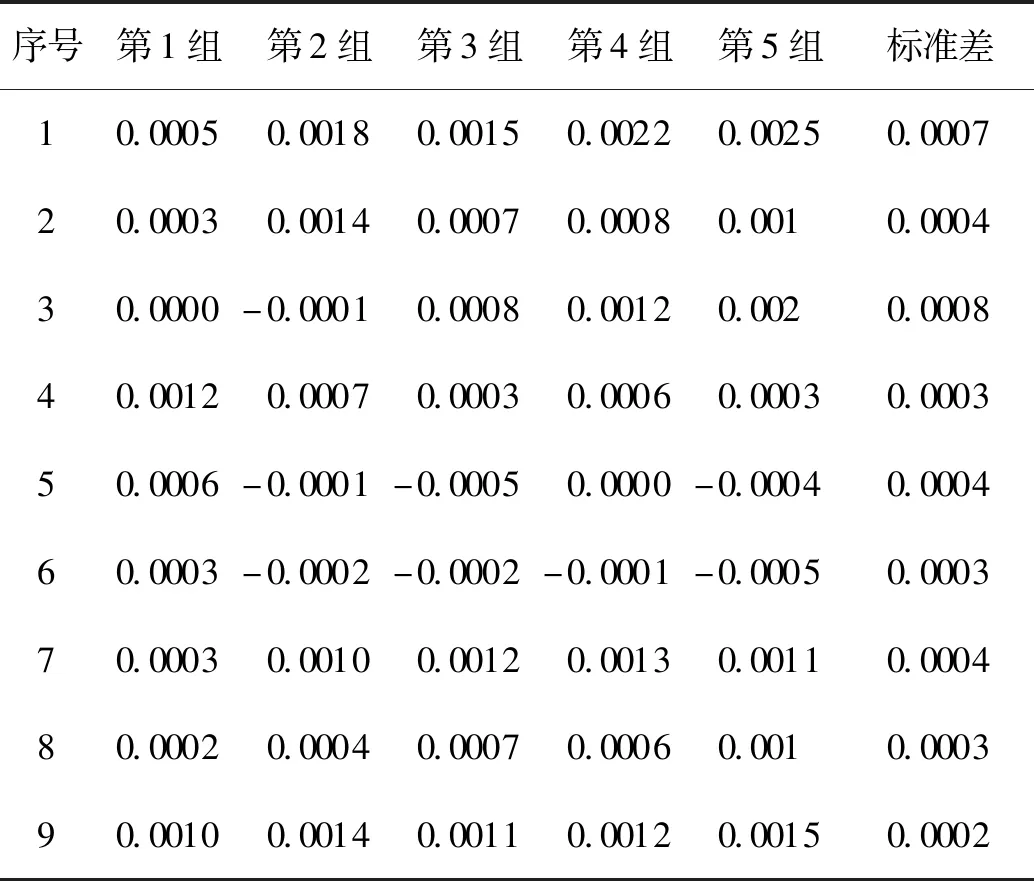
表6 几何重心法:正反像素差值和标准差Tab.6 The geometric center of gravity method—positive and negative pixel differences and standard deviation pixel
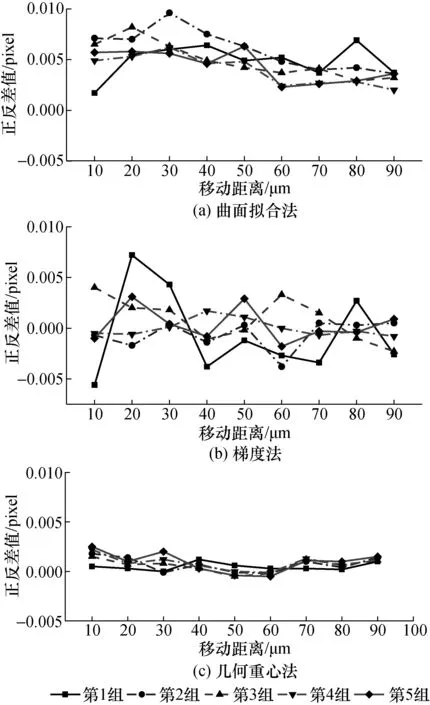
图8 3种算法的正反像素提取差值曲线Fig.8 The difference curve of positive and negative pixel of the three algorithms
图8显示同一刻度之下的5组实验数据的正向与反向像素差值波动性。从图8中可以看出,几何重心法的差值波动最为平稳、且差值也最小。
表7、8、9分别为曲面拟合法、梯度法和几何重心法,以图像0为参考图像的像素提取值以及与相邻图像之间的累计像素提取值之间的误差值。从数据中可以明显看出,几何重心法的像素提取值与相邻图像之间的累计像素提取值之间的误差值波动最小、误差值也最小,表明几何重心法相比较曲面拟合法和梯度法,其像素提取值具有更好的线性度。
图9显示同一刻度之下的5组实验数据的线性误差值波动曲线。从图9中可以看出,几何重心法的线性误差值的波动最为平稳、且误差值也最小。
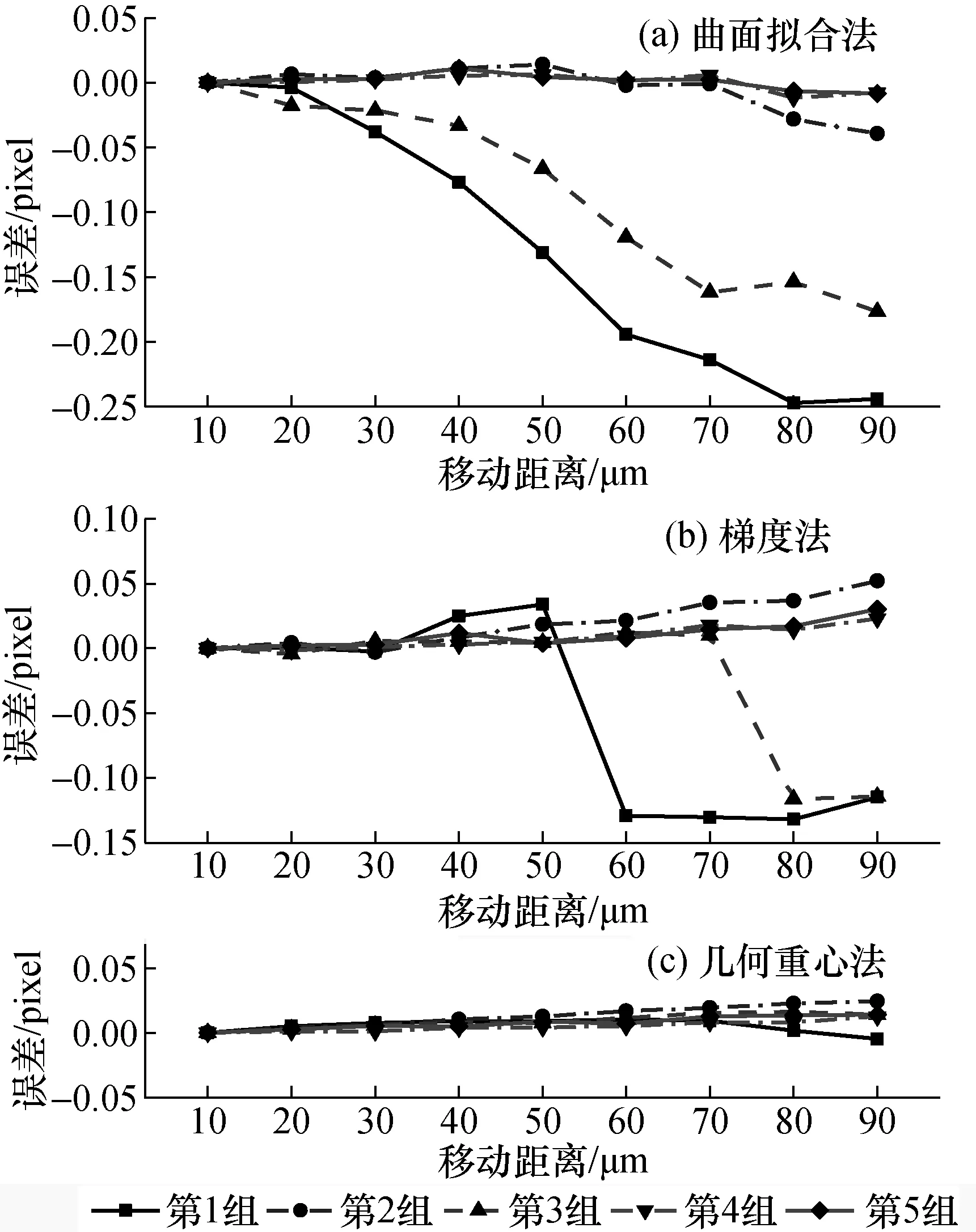
图9 3种算法的线性误差值曲线Fig.9 The linear error value curves of the three algorithms
曲面拟合法、梯度法和几何重心法3种亚像素提取算法所需的时间(包括整像素提取时间)分别为2.233 4 s、5.317 6 s和<0.2 s。可以看出,几何重心算法相比较其他两种算法用时短,符合超低速转速的在线测量要求。
5 结 论
本文提出一种基于影像技术的超低转速的在线测量方法,提出的几何重心法的亚像素提取算法,具有算法原理简单、计算效率高等特点。

表7 曲面拟合法:图像0与图像n之间像素值及线性误差值Tab.7 The curved surface fitting method—pixel value and linear error between image 0 and n pixel
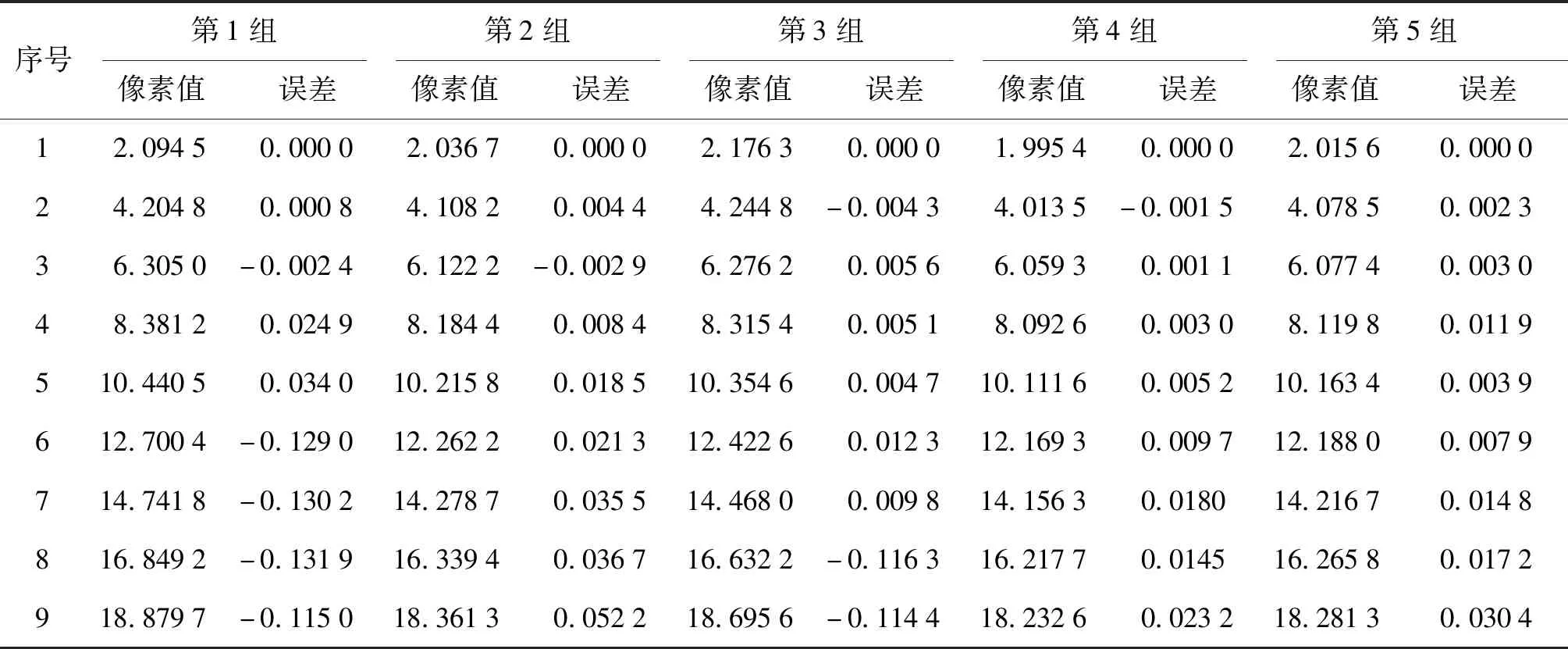
表8 梯度法:图像0与图像n之间像素值及线性误差值Tab.8 The gradient method—pixel value and linear error between image 0 and n pixel
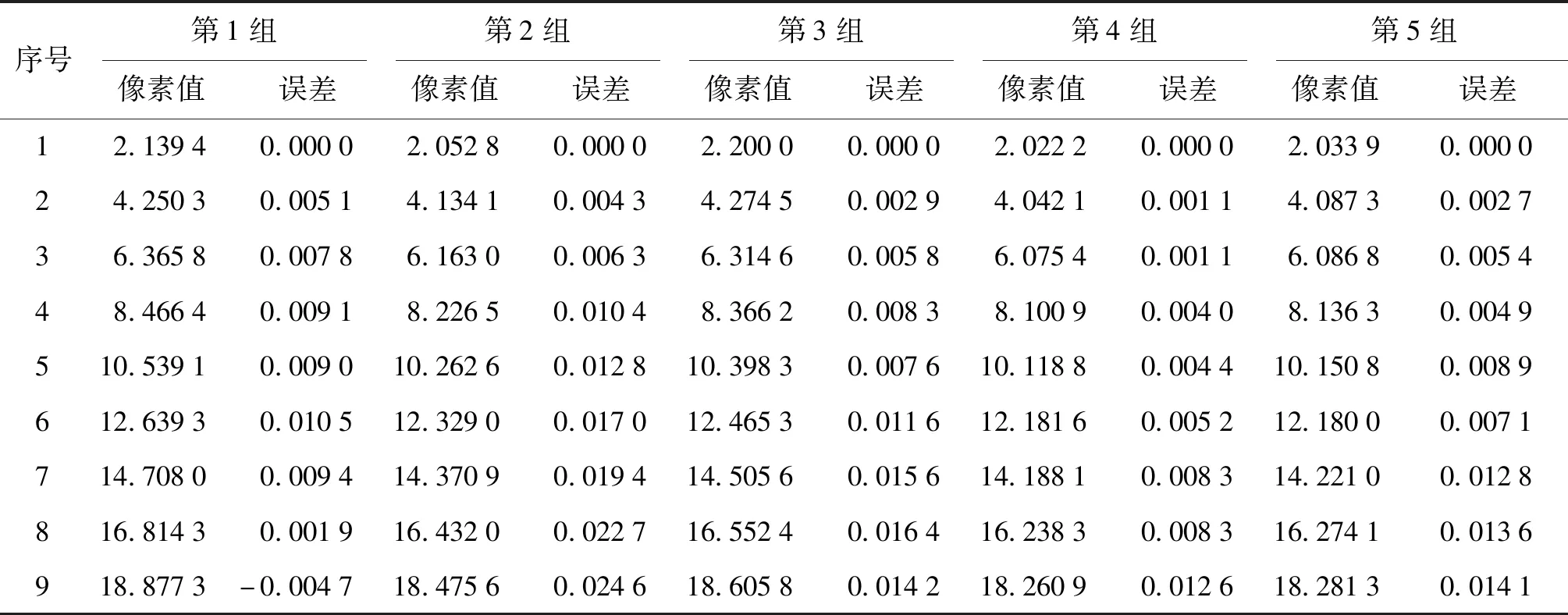
表9 几何重心法:图像0与图像n之间像素值及线性误差值Tab.9 The geometric center of gravity method—pixel value and linear error between image 0 and n pixel
综合实验结果表明:几何重心法在亚像素提取值的线性度、重复性以及稳定性等方面都优于曲面拟合法和梯度法。因此,将几何重心法用于超低转速测量中的亚像素提取算法是一种较好的选择方法。
