有约束随动系统控制策略研究

付荣荣, 李东玉, 田永胜, 王 涵

(燕山大学 电气工程学院,河北 秦皇岛 066004)

1 引 言

有能量约束、复杂、不稳定、非线性等特性是随动系统的典型特点[1]。这就要求构建控制系统的时候在保证系统稳定的前提下,尽可能地提高系统反应速度和跟随信号的准确性。在实际工程中面对各种错综复杂随动系统,通过研究不同的控制算法在控制系统中的效果来验证该算法的理论可行性和实用性。验证过程需要一个典型的平台,既可以有效反映算法的优劣程度,同时可以直观地体现控制效果,并且价格低廉,结构简单,易于实现。基于以上需要,本文提出了一种基于现实生活的典型模型,类似于现实世界中保证水无溢出前提下杯子的水平移动过程。该过程被抽象为用一个碗运送一颗球,球在碗中振荡但移动过程球不能掉出碗外。该模型是一个典型的随动系统,它要求在临界能量值之下控制被控对象,所包含的耦合性、约束限制等特点都是在研究有约束随动系统时所关心的问题,因此对该模型的建立与分析具有重要的意义[2～5]。

2 系统建模

碗球系统的数学分析模型如图1所示,在碗受到水平力F的作用时,球和碗共同运动并产生偏角θ,球除了受到自身重力外,碗对球还有一个径向的支持力T。被控系统中碗质量M=5 kg,F=1 N(外力),球质量m=1 kg,碗半径l=0.5 m。对球的快速控制与定位问题可以抽象为：小碗在受到外力F(t) 作用时,使得小碗在最短的时间ts由A点运动到B点,且摆球摆角θ小于系统允许的最大摆角0.5 rad。

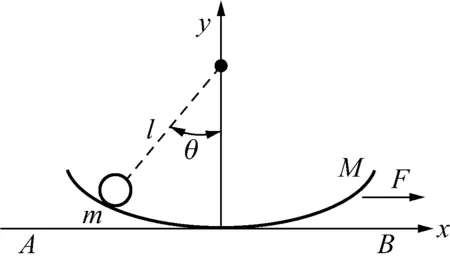
图1 碗球系统的数学分析模型Fig.1 Mathematical Model of Cup-ball system

基于动力学模型,采用基于达朗伯原理-动静法求解该系统的非线性微分方程,并完成系统的状态空间描述[6,7]及能控能观性分析。

以球为研究对象建立广义坐标系,如图2所示,取x、θ为广义坐标对建立运动微分方程有：

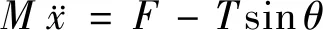
(1)

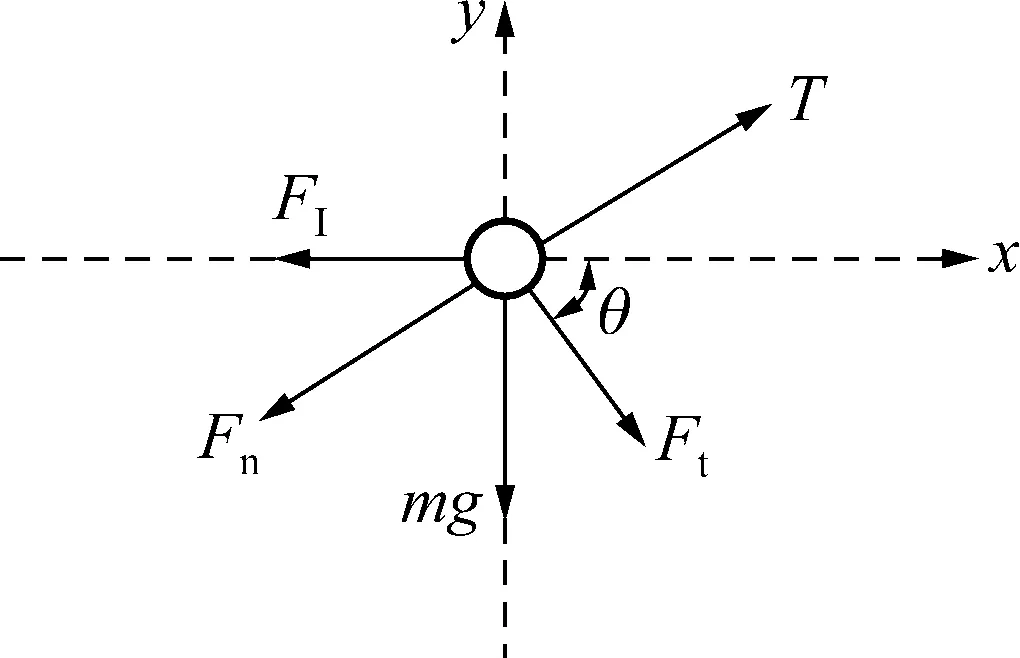
图2 小球受力分析图Fig.2 Force analysis of ball

根据达朗伯原理对球进行受力分析,它受重力mg,绳张力T,法向惯性力Fn,切向惯性力Ft,水平惯性力FI。在水平方向上建立平衡方程有：

Tsinθ-FI+Ftcosθ-Fnsinθ=0

(2)

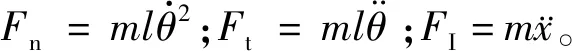
(3)

则：

(4)

在切线方向上建立平衡方程有：

(5)

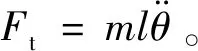
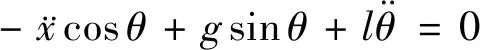
(6)

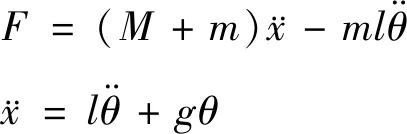
(7)

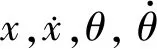
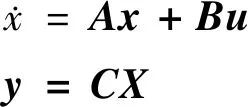
(8)

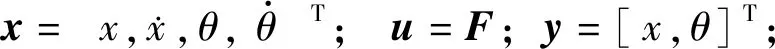
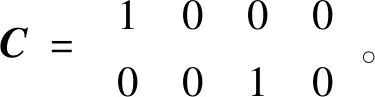
该系统的能观性判别矩阵为：

(9)

其中:M、m为有限值则：|Qo|≠0,rankQo=n系统完全能观。

系统的能控性判别矩阵为：

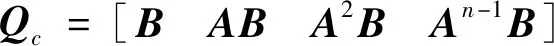
(10)

其中M、l为有限值则：|Qc|≠0,rankQc=n,系统完全能控。

3 极点配置的状态反馈控制器设计

极点配置步骤：

1) 判断系统是否完全能控。根据上文讨论系统在l和M为有限值的情况下完全能控。

2) 推导写出系统传递函数的能控标准型。所研究的碗球系统的特征方程为：

(11)

系统是能控的则存在线性非奇异变换：

(12)

系统状态空间表达式化成：

(13)

其中:

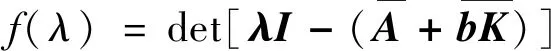
(14)

4) 根据给定的期望特征值,确定闭环系统的期望特征多项式f(λ′)。

5) 比较f(λ)和f(λ′)各对应项系数得,

(15)

(16)

根据上述步骤对系统进行极点配置,引入状态反馈律u=-Kx+v,可得闭环系统动态方程为：

(17)

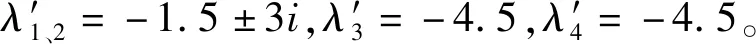
图3 闭环系统结构图Fig.3 Structure of close-loop system

4 遗传算法优化的LQR最优控制法

4.1 LQR最优控制

LQR最优控制中,一个最关键的问题就是二次型性能指标中加权矩阵Q和R的选取。由系统方程：

(18)

建立最佳控制向量的矩阵K：

u(t)=-Kx(t)

(19)

定义该系统的性能指标为：

(20)

式中X*QX为运动状态约束的二次型,其中Q为运动约束矩阵,对称半正定矩阵。u*Ru为控制输入约束的二次型,其中R为约束控制矩阵,对称正定矩阵。把加权矩阵选为对角矩阵,即Q=diag(q1,q2,q3,q4)。这样性能指标J可以表示为：

(21)

由式(21)可以看出,qi是对xi的平方的加权,R是对控制量u平方的加权。

4.2 遗传算法对加权矩阵Q、R的优化

遗传算法(Genetic algorithm,GA)是一种自适应全局优化概率搜索算法。利用遗传算法对线性二次最优控制的加权阵和进行优化[8～10]。具体步骤如图4所示。

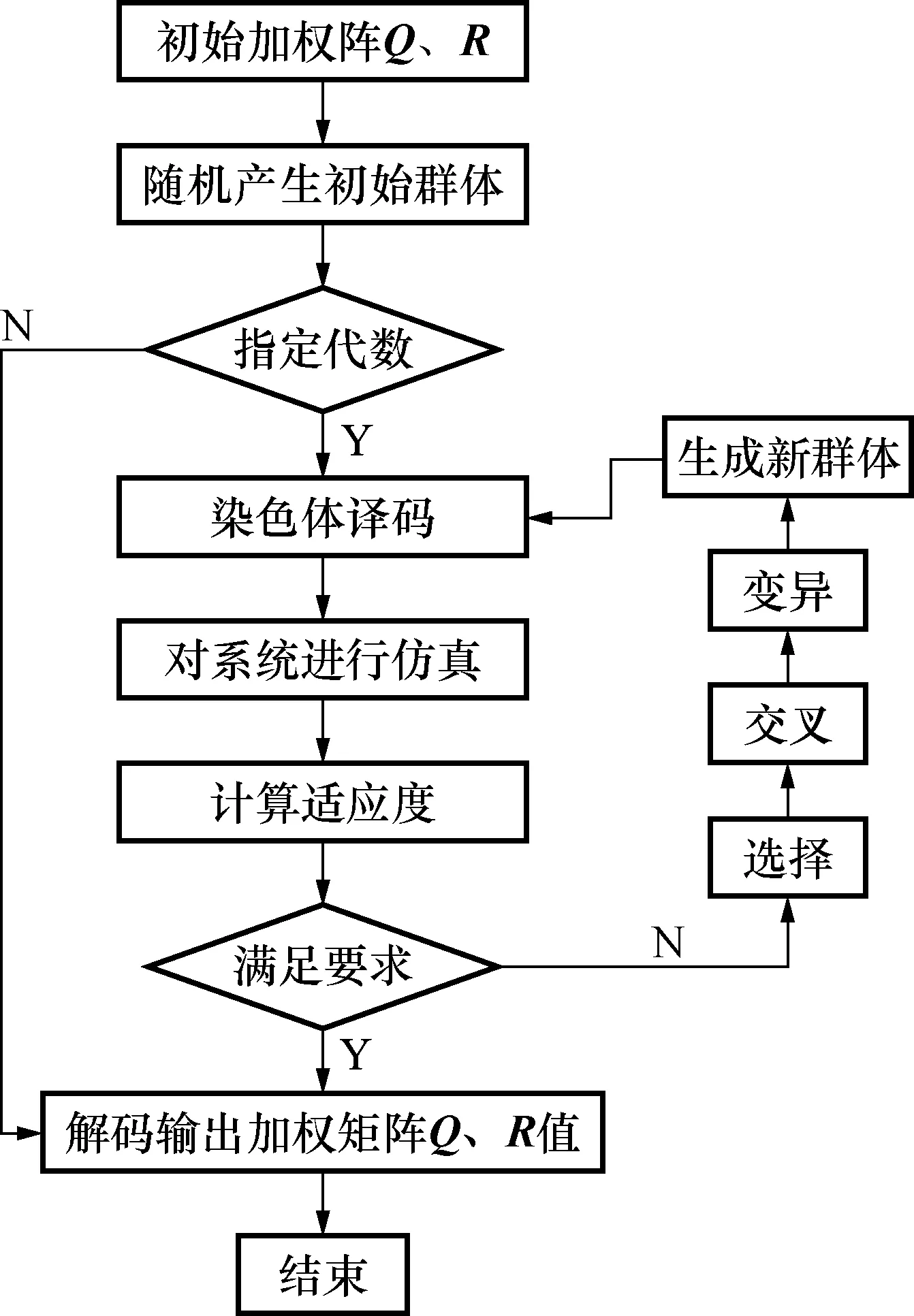
图4 遗传算法对加权矩阵优化流程图Fig.4 Flow chart of weighted matrix optimization by GA

5 仿真结果的对比分析

极点配置的状态反馈控制器和遗传算法优化的LQR控制的仿真图分别如图5所示。图5中在单位阶跃作用下,2种控制方法的响应曲线的大致趋势是一致的。碗位移的输出大概是一个常数1,达到了碗定位的效果。而摆线倾角最大值都小于系统允许最大摆动角0.5rad,并且最终输出都逐渐趋向于0,达到了控制小球摆动防止小球滑落的控制要求,均很好地改善了控制系统性能。对图5进行对比计算分析可得如表1数据。

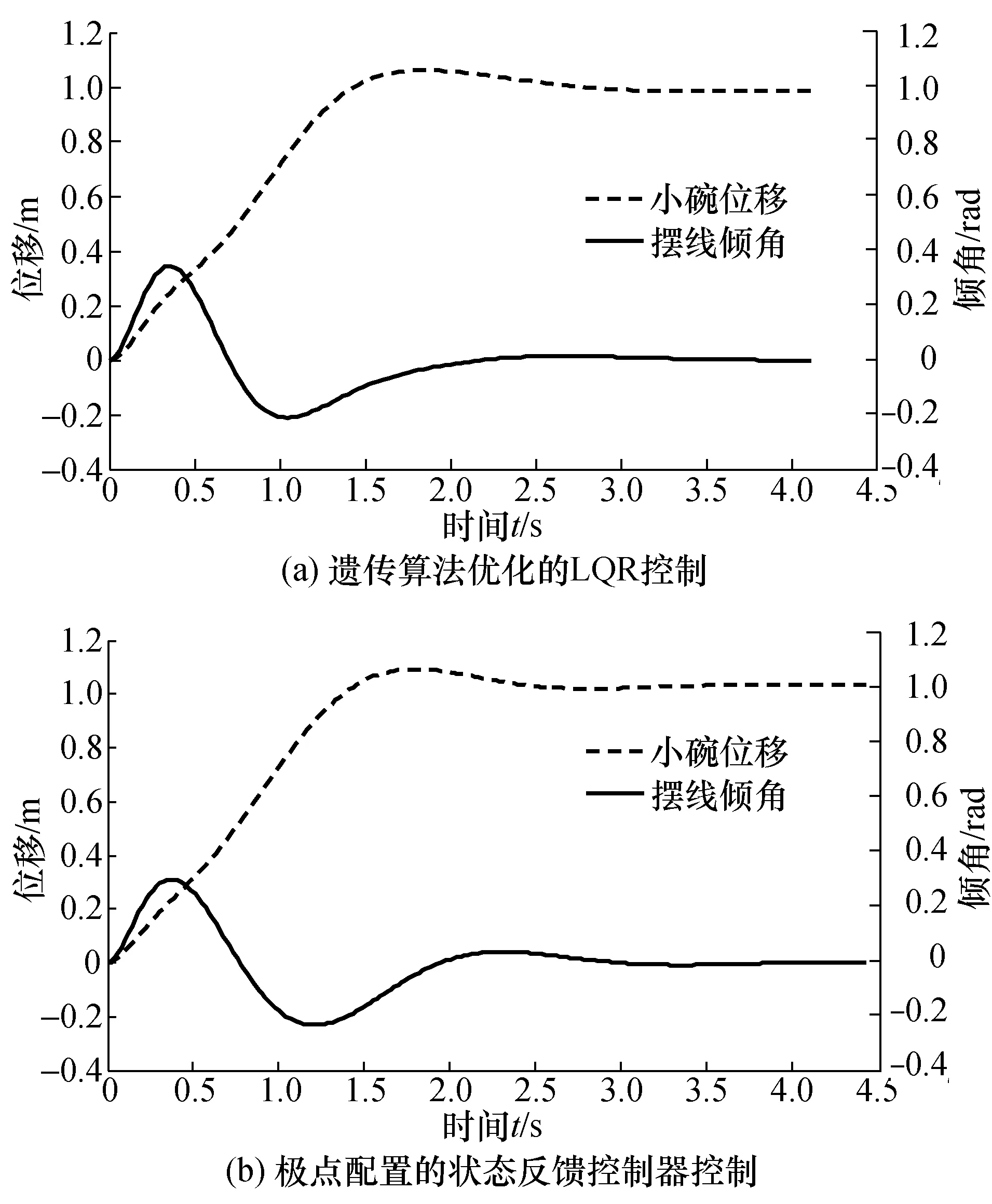
图5 2种控制方法仿真结果图Fig.5 Simulation results of two control methods

具体的,二者的控制效果存在着差别。极点配置的状态反馈控制对位移和摆角控制的最大动态偏差分别为0.05 m和0.29 rad,远小于遗传算法优化LQR控制的0.08 m和0.35 rad,说明其具有更好的鲁棒性和瞬态特性。而遗传算法优化的LQR控制调节时间也要远小于前者尤其是对球摆角的控制方面,LQR控制器的调节时间为2.2 s,而极点配置法为2.8 s,且前者具有更小的震荡次数,这表示LQR控制器的控制效率更高且具有较优的稳态特性。在参数选择方面,极点配置的状态反馈控制器从系统的整体入手,方法简单但需要反复进行极点配置计算,寻求最优解。而遗传算法优化LQR控制控制器可以有针对性地重点考虑x,θ在u控制下的变化规律,并根据系统的实际情况通过迭代获得误差更小的最优解,参数的选择更优针对性,可移植性高,便于应用。

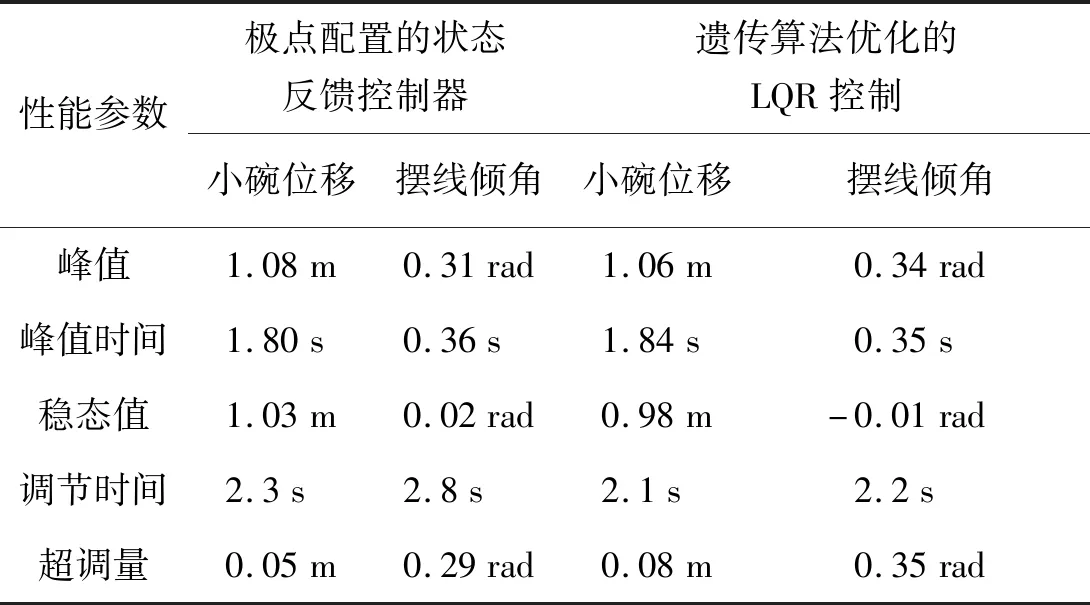
表1 2种控制方法控制效果对比Tab.1 Comparison of two control methods

6 结 论

本文提出了一种新的典型的随动系统,并利用达朗伯静力学的方法对系统进行了建模。在讨论系统能控能观性的基础上,分别设计了极点配置的状态反馈控制器和遗传算法优化下的LQR控制器,并利用Matlab进行了控制效果的仿真并对比分析,通过比较可知极点配置的状态反馈控制器具有更好的鲁棒性和瞬态特性,对于对参数变化和超调量要求比较高的系统有更好的控制效果。而遗传算法优化的LQR控制具有更好的稳态特性,对于对响应时间以及调节时间要求比较高的系统有更好的控制效果。同时在参数选择方面相比于极点配置试特征值的方法,遗传算法优化LQR控制控制器更有针对性,便于实际的应用操作,是搭建控制系统的良好选择。