某组合结构厂房阻尼比分析

范晓斌

(上海电气集团国控环球工程有限公司，山西 太原 030000)

1 概述

阻尼比在组合结构中已经超出了经典的结构阻尼，属于非经典结构阻尼，虽然目前对于非经典结构阻尼的计算方法较多[1]，大多[2-4]采用复振型方法进行分析，但由于该方法的复杂性而未得到工程师的广泛认可，而造成其取值成为目前国内比较具有争议的问题，文献[6]中11.3.5条给出了组合结构在多遇地震作用下的阻尼比可取为0.04；而在广州432 m高西塔楼组合结构和山西中医学院组合加层结构中取值阻尼比0.035，均不同于单一材料的阻尼比；文献[5]中提到对于组合结构取单一阻尼比不合适，建议采用电算比较方便的应变能因子法进行抗震计算；影响阻尼比的主要因素是组成结构的材料刚度，但如何考虑刚度对阻尼比的量化取值，目前还没有界定，本文从工程实践出发，主要研究了钢材对组合结构阻尼比的影响。

2 工程背景

某项目为组合结构，8度(0.02g)，场地类别Ⅲ类，地上8层，上部4层为钢结构，下部为混凝土结构，层高6.5 m, 建筑高度52 m，主要构件截面如下所示：

1)钢柱采用H500×500×18×22的钢柱;2)钢梁采用H650×300×18×20;3)混凝土柱采用b×h=750×750;4)混凝土梁采用b×h=450×600;5)支撑采用H400×400×21×28。

3 计算理论

组合结构中因使用了不同材料，经典阻尼矩阵已不能准确反映结构抗震性能，而在满足工程需要的前提下MIDAS/GEN软件通过应变能因子方法引入组阻尼比计算各个振型的阻尼比，其中结构的第i个振型的阻尼比可根据所有单元的第i振型的能量和来计算，即式(1)。

(1)

其中,ED为消散能;ES为应变能。

4 MIDAS/GEN建模及分析

4.1 结构模型

首先根据结构的特点与实际尺寸，按照实际工程尺寸分层建模[8]，如图1所示。

然后经过Pushover分析得到结构塑性铰分布如图2所示，从图2中可以看出结构的薄弱位置基本上均发生在三、四层位置，而且上部钢结构部分的塑性铰基本都发生在支撑和梁端，符合抗震主次构件的设计。

最后建立4+1,4+2,4+3,4+4 4种模型如图3所示。

4.2 模态分析结果

表1 组合结构模型周期比

由表1中可以看出结构扭转效应并不明显，符合《高规》规定。

4.3 反应谱分析结果

4.3.1刚度比分析

刚度比是控制结构竖向不规则性和薄弱层的重要指标。文献[7]第3.4.3条规定，“混凝土房屋、钢结构房屋和钢—混凝土混合结构房屋存在表3.4.3-2所列举的侧向刚度不规则，即其楼层侧向刚度不宜小于相邻上部楼层侧向刚度的70%或其上相邻三层侧向刚度平均值的80%。”本文通过反应谱分析得到了该结构的薄弱层为第三、四层，即混凝土与钢结构交接处及下一层为薄弱层，这与前面Pushover分析得到的结构基本一致，其各层侧向刚度如表2所示。

表2 组合结构各层侧向刚度

由表2可以看出结构在竖向存在不规则现象，当结构发生大震时极易在这个部位倒塌。且层刚度与层数关系不大，所以竖向不规则部位基本不变，在此不作赘述。

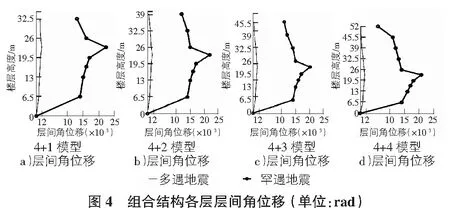
4.3.2层间角位移分析

通过图4可以发现，无论是多遇地震，还是罕遇地震情况下，组合结构的层间角位移基本符合各自材料组成结构层间角位移与层高之间关系的曲线，而上部的钢结构由于设置了支撑，普遍小于下部混凝土结构的层间角位移；最大层间角位移位置并未随着钢结构层数的增减而发生变化，都在3层～4层之间，这也再次证明了层数对层刚度的影响不大，即薄弱层也是层间角位移最大的部位；总体上来看，结构从弹性阶段到弹塑性阶段，其薄弱层即为该结构的关键部位，如图3所示；通过关键部位及节点角位移相关数据整理分析，可以比较全面地反映结构的弹塑性阶段的工作性能。

5 组合结构阻尼比的选取

5.1 单一阻尼比下的反应谱分析

考虑到层刚度主要与梁、柱及墙的截面尺寸和形状及层高关系密切，所以本文通过结构从多遇地震到罕遇地震作用下，薄弱层由弹性阶段到弹塑性阶段的发展过程，以薄弱层层间角位移为指标，讨论钢结构不同层数下对单一阻尼比的影响关系，通过反应谱分析结果可知，4个模型下阻尼比关键层层间角位移如表3所示。

表3 组合结构薄弱层单一阻尼比下层间角位移 rad

5.2 组阻尼下的反应谱分析

考虑到层刚度主要与梁、柱及墙的截面尺寸和形状及层高关系密切，所以本文通过结构从多遇地震到罕遇地震作用下，薄弱层由弹性阶段到弹塑性阶段的发展过程，以层间角位移为指标，讨论不同材料不同层数下对组阻尼比的影响关系，通过反应谱分析结果可知，4个模型下阻尼比关键层层间角位移如表4所示。

表4 组合结构薄弱层应变能因子法层间角位移 rad

5.3 两种分析方法下进行比较

运用4种模型选用单一阻尼和组阻尼分别计算得到的薄弱层层间角位移，通过分析比较可知，阻尼比的选取对混合结构在地震作用下的分析影响较大，且与组成结构的材料刚度有着密切的关系，从数据中可以看出4+4模型中当单一阻尼比取0.032时与组阻尼下计算的层间角位移基本一致，而随着钢结构层数的减少单一阻尼比选的越大，与组阻尼下计算的结果也就越接近。

6 结论

通过上述数据分析，本文提出在进行类似组合结构地震作用计算时阻尼系数应取ζ=0.03～0.045，即:当钢结构所占组合结构的刚度达到50%以上时，宜取阻尼比ζ=0.03～0.032；当钢结构所占组合结构的刚度达到40%～50%时，宜取阻尼比ζ=0.032～0.035；当钢结构所占组合结构的刚度达到30%～40%时，宜取阻尼比ζ=0.035～0.038；当钢结构所占组合结构的刚度小于30%时，宜取阻尼比ζ=0.038～0.045。