竖向非均质饱和地基中埋置扭转荷载的动力响应

邹新军，贺琼，覃玉兰

（湖南大学 土木工程学院，湖南 长沙410082）

弹性半空间的动力响应问题在岩土工程中具有举足轻重的地位，该问题在土-结构物的动力相互作用、地震工程、基础振动等领域均引起了国内外学者的关注. 随着我国经济发展，近海工程建设如火如荼，如跨海大桥、海上风力发电机以及海上平台等，这些结构物受力较复杂，不仅要承受自然环境产生的风力、波浪力以及地震荷载，还要承受使用过程中的运转荷载，其不可避免地会受到扭转荷载的影响.同时，实际工程中基础大多具有一定埋深，基础承受扭转动荷载时，周围土体亦会承受基础所传递的埋置扭转动荷载，因此研究弹性半空间中埋置扭转荷载的动力响应问题，有助于进一步掌握地基基础的承载变形特性.

Lamb[1]最先对弹性半空间的动力学问题进行研究，其分别考虑了半空间表面作用和内部埋置的法向线荷载与点荷载等四种典型荷载.Chao[2]研究了弹性半空间表面受水平、竖向荷载时的动力响应问题.王贻荪[3]研究了竖向集中简谐荷载作用于弹性半空间表面的问题，采用拉普拉斯变换方法获得了特定条件下半空间表面位移的精确解.Reissner 和Sagoci[4]首次研究了弹性半空间表面基础受扭转荷载作用下的响应问题.Rahman[5]在Reissner 的理论基础上进一步对弹性半空间内部埋置刚性板的扭转振动问题进行了研究.自Biot[6]提出饱和多孔介质波的传播理论，并推导出土体的多维固结方程以来，不少学者开始在此理论基础上研究饱和半空间的动力学问题.Philippacopoulos[7]考虑多孔弹性半空间中埋置点源荷载，利用傅立叶变换与汉克尔变换方法求解地基土的位移.陈胜立等[8]对饱和地基中埋置简谐竖向集中荷载下的动力响应问题进行研究，分析了饱和地基土表面竖向位移的变化规律.Chen 等[9]研究饱和地基中埋置任意荷载的三维动力响应问题，求解了弹性半空间中的应力、位移分量.张智卿等[10]研究了均质非饱和滞回阻尼土层中弹性支撑桩的扭转振动.陈刚等[11]对半空间饱和土体中埋置扭转简谐荷载的稳态响应问题进行研究，分析了土体参数对响应的影响规律.

以上研究均视地基为各向同性弹性半空间，但实际上地基土在沉积过程中会受到各个方向有效应力的影响，具有一定的各向异性，主要有径向非均质性和竖向非均质性两种情况.Naggar[12]研究了径向非均匀地基中土体的竖向、扭转动力响应.Zhang 等[13]考虑地基土的径向非均匀性（将桩周土沿径向分为n圈层，每个圈层为剪切模量不同的均质各向同性弹性体），研究弹性半空间中单桩的扭转振动响应问题.Awojobi 等[14]考虑弹性半空间的竖向非均质性，假定土体剪切模量随深度线性变化，对半空间的平面应变与轴对称问题进行了研究.邹新军等[15]基于桩侧土双折线模型，探讨了地基土分层时单桩的受扭性状.王国才等[16]对层状地基中单桩的扭转振动问题进行研究，采用积分变换及Muki 虚拟桩的方法求解并分析了桩土参数对动力响应的影响.Wroth[17]等认为土壤沉积时的地质环境和荷载历史随着时间而发生变化，故假定土体剪切模量随深度呈非线性分布更符合实际.Rajapakse[18]假定土体剪切模量随深度分别呈幂函数与指数函数非线性分布，采用经典变分定理的方法来分析荷载传递问题.邹新军等[19]考虑地基土的剪切模量随深度非线性分布，对单桩静力受扭问题进行了弹塑性分析，但相应的动力扭转分析仍属鲜见.

天然地基土通常在竖向呈现非均匀性，其剪切模量、渗透系数及孔隙率等均随深度发生变化，为简化问题，本文主要考虑剪切模量随深度的非线性变化，即假定地基土的剪切模量随深度呈指数函数非线性分布，基于Biot 固结理论与弹性动力学原理，建立饱和地基土中作用简谐扭转荷载下的动力微分方程，引入边界条件并利用Hankel 变换与逆变换求解获得饱和地基土中的剪应力与切向位移解答，据此基于Mathematica 编制出相应的计算程序，进一步进行参数分析并讨论土体参数对地基土中埋置简谐扭转荷载动力响应的影响规律.

1 基本扭转动力微分方程的建立

弹性半空间中埋置简谐扭转荷载问题可在柱坐标系下建立简化分析计算模型，如图1 所示，其中：弹性半空间地基内部z = h 处作用埋置简谐扭矩T0eiωt（ω 为频率，i=（-1）1/2），荷载作用范围是半径为a 的圆形区域.

许多学者在研究扭转问题时，为进一步简化问题均做出一定假定，如张智卿[10]、Naggar[12]、Rajapakse[18]等，为建立问题的基本方程，本文参照已有文献特做出如下假定：

1）视地基为弹性半空间，其表面为自由面.

2）假定地基土的剪切模量Gs随深度呈指数函数非线性分布：

式中：μ 为地表处土体剪切模量（Pa），可按μ=ρsvs2计算，其中vs为地表处土体剪切波速（m/s），ρs为土骨架密度（kg/m3）；α 为非均匀系数，可按文献[18]取值.

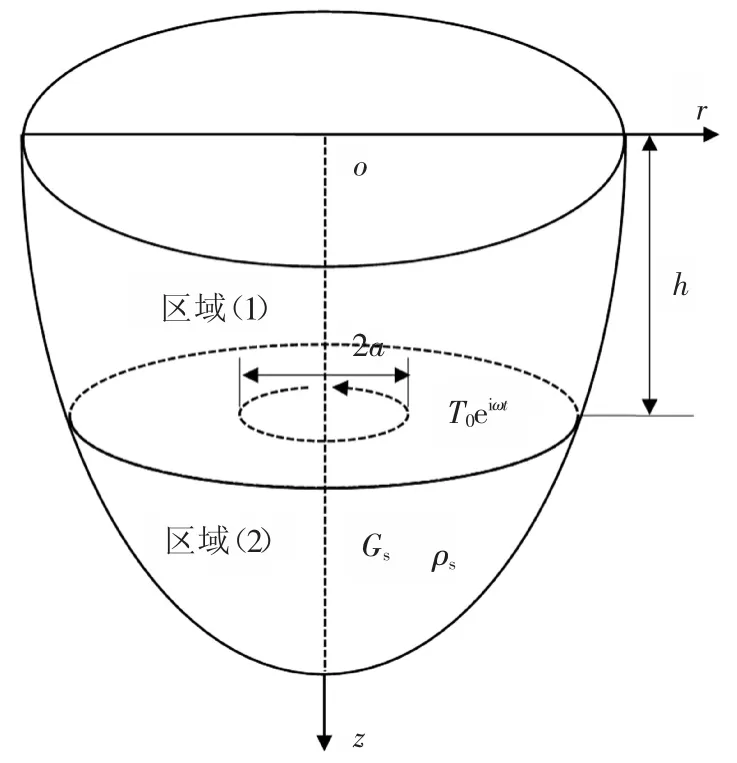
图1 饱和地基中埋置简谐扭转荷载简化分析模型Fig.1 Simplified analysis model of buried torsional load in non-homogeneous saturated soil

3）地基土的扭转振动为小变形，只考虑土骨架切向位移uθ（r，z，t）eiωt和孔隙水相对于土骨架的切向位移wθ（r，z，t）eiωt，为书写方便下文省略简谐因子eiωt.

4）假定简谐扭转荷载作用范围内，扭转剪应力F（r）与半径成正比例关系，则荷载作用面处扭转剪应力分布函数为：

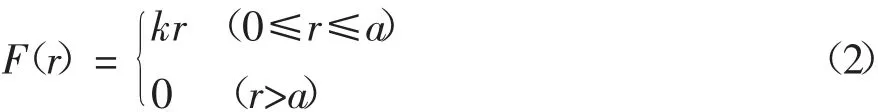
式中：k 为比例系数.

基于上述假定，根据Biot 固结理论可建立埋置简谐扭转荷载作用下饱和地基土的基本扭转动力微分方程：

式中：ρ= （1+n）ρs+nρw，其中ρw为孔隙水的密度（kg/m3），n 为孔隙率.

轴对称问题中流体（孔隙水）的运动方程为：

式中：kd为地基土的动力渗透系数（m/s）；g 为重力加速度（m/s2）.

根据土骨架的剪应力-位移关系，可得地基土的剪应力表达式为：

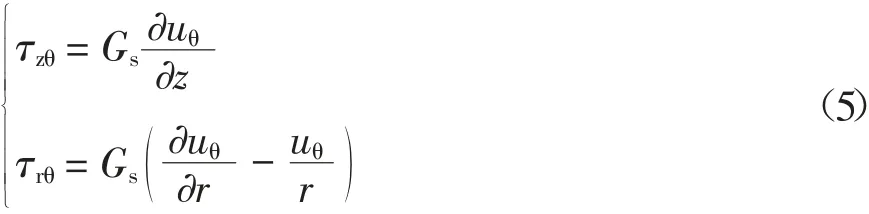
式中：τzθ、τrθ分别为地基土的剪切应力（Pa）.

引入如下无量纲参数与变量：r=r/a、z=z/a、μθ=μθ/a、τ=τ/μ、h=h/a、ρw=ρw/ρ、Gs=Gs/μ、f=aω（ρ/μ）1/2，其中f 表示无量纲频率，则饱和地基基本扭转动力微分方程式（3）与流体运动方程式（4）可分别化为：

而地基土的剪应力-位移关系式（5）同样经无量纲化后可变为：

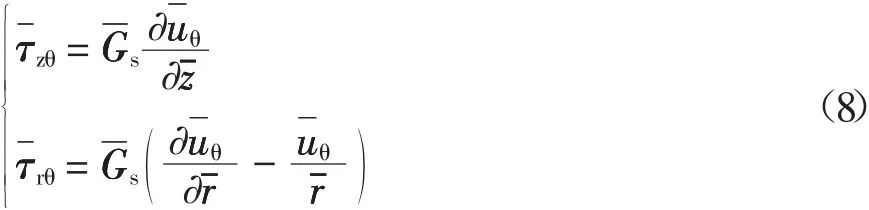
为便于求解上述饱和地基中埋置简谐扭转荷载作用下的基本扭转动力微分方程，对式（6）与式（7）分别进行Hankel 变换并整理可得：

同样，地基土的剪应力-位移关系式（8）经Han－

kel 变换后变为：式中：τzθ1为τzθ的一阶Hankle 变换式，τrθ2为τrθ的二阶Hankle 变换式.

2 基本扭转动力微分方程的求解

为求解剪切模量呈指数函数非线性分布的地基土扭转动力响应，将剪切模量分布式（1）代入饱和地基土的基本扭转动力微分方程式（9）中并化简：

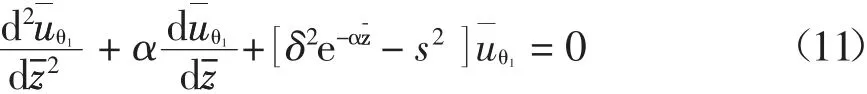
为求解微分方程式（11），构造两个辅助函数：

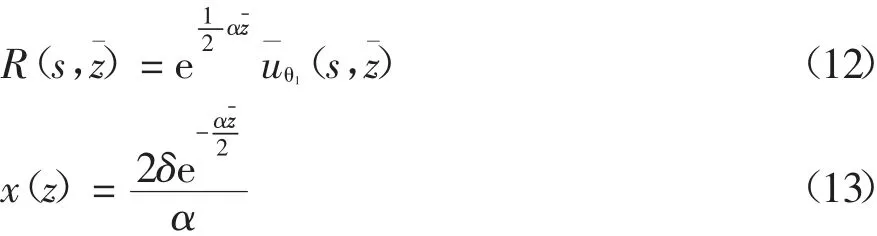
并将其代入微分方程式（11）中化简得：

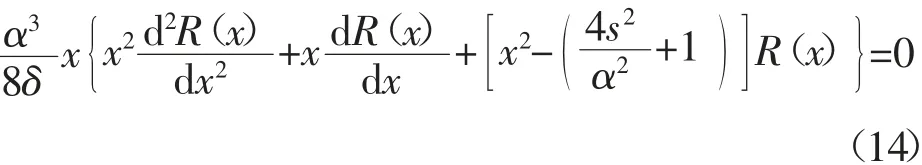
进而可求得：

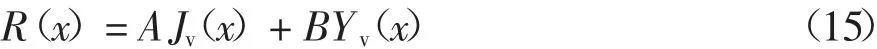
式中：Jv（x）、Yv（x）分别为v 阶第一、二类贝塞尔函数，其中v=（1+4s2/α2）1/2；A、B 是与s 相关的待定系数，可引入相应的边界条件后计算确定.

将式（15）代入式（12）与式（13）中可得土体基本扭转动力微分方程式（11）的解为：

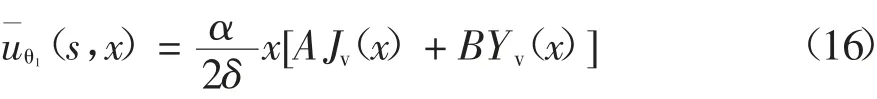
根据地基土的剪应力-位移关系式（10）可获得土体的剪应力分布：

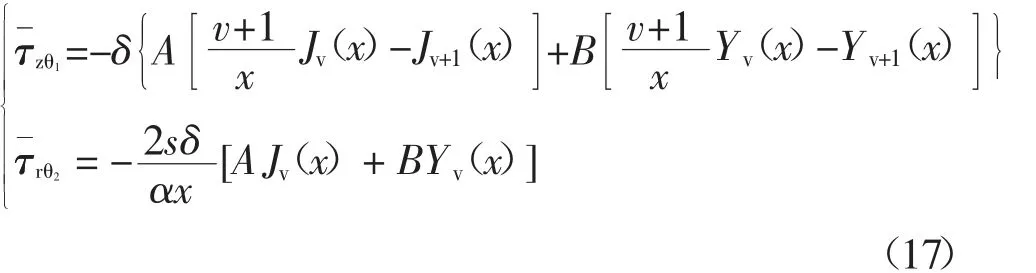
3 边界条件与待定系数求解

为了求解所得解答式（16）与式（17）中的待定系数A、B，首先需要确定相应的边界条件.由图1 所示弹性半空间中埋置简谐扭转荷载的简化计算分析模型可知，荷载作用面将半空间分为区域（1）与区域（2）两部分，根据基本扭转动力微分方程的解式（16）以及土体的剪应力分布式（17）可得区域（1）、（2）的切向位移、剪应力表达式分别为：

区域1：0 ≤z ≤h，即（2δe-αh/2）/α≤x≤2δ/α

由弹性半空间介质中扭转波的辐射条件可知：区域（2）中剪应力、切向位移解答中待定系数B2=0.

弹性半空间饱和地基表面为自由面，则地表处的剪切应力为零：

饱和地基中埋置简谐扭转荷载作用面处应满足位移连续性条件与应力间断性条件：

式中：F（1s）为荷载作用面处剪应力分布函数的一阶Hankel 变换式：

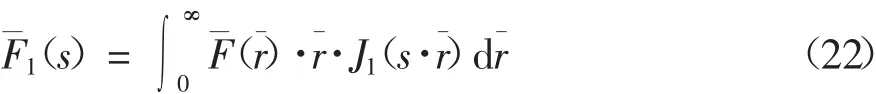
式中：F（r）为荷载作用面处扭转剪应力F（r）的无量纲形式：

将边界条件式（20）与式（21）代入式（18）与式（19）中，可求得待定系数B1、A1、A2分别为：

式中：x1=2δ/α，x2=（2δe-αh)/α，η=δ{Jv（x2）[（v+1）Yv（x2）-x2Yv+1（x2）]-Yv（x2）[（v+1）Jv（x2）-x2Jv+1（x2）]}.

将待定系数表达式（24）代入到饱和地基土的切向位移式（18）与剪应力式（19）中可获得Hankel 变化域内的剪应力、切向位移解答，并将该解答进行Hanke 逆变换即可得到饱和地基土的应力位移.

根据上述获得的地基土应力位移解答，采用Mathematica 编制出Hankel 逆变换的数值积分程序，用以计算埋置简谐扭转荷载作用下竖向非均质饱和地基中的最终剪应力与切向位移.

4 结果验证与参数分析

4.1 结果验证

为验证本文推导结果的正确性，令α→0，则土体剪切模量Gs不随深度z 变化，此时问题退化为均质饱和半空间中埋置扭转荷载作用的动力响应问题，与陈刚等[11]的理论解进行对比（如图2），计算参数为：地表处剪切模量μ=9.4×106Pa，孔隙率n=0.4，土颗粒密度ρs=2 650 kg/m3，水的密度ρw=1 000 kg/m3，土体动力渗透系数kd=10-7m/s，扭转荷载频率f=1、埋深h=8，计算深度z=8.8.从图2 可看出，本文退化结果与已有理论解吻合较好，从而验证了本文解的正确性.

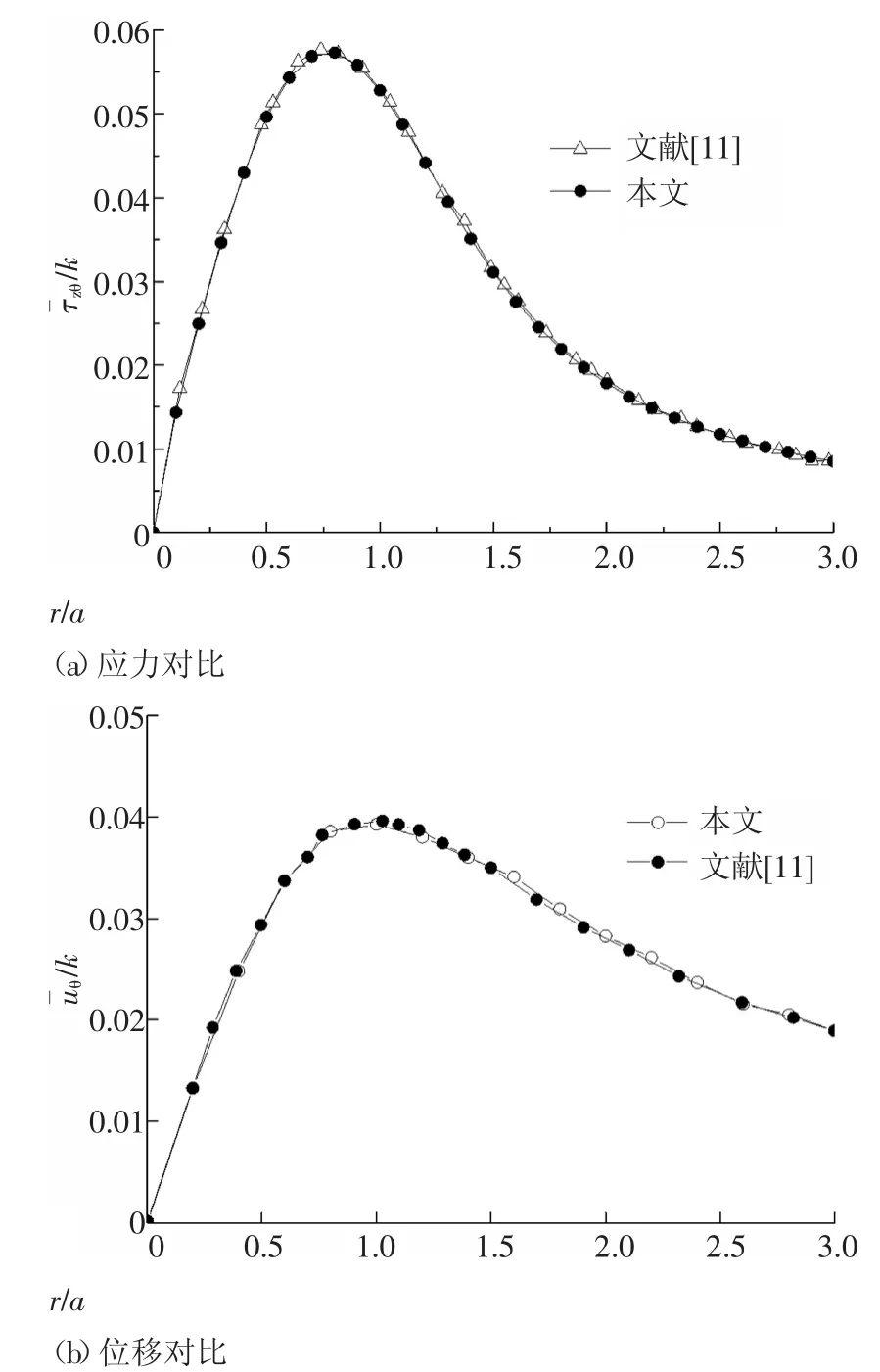
图2 本文结果与文献[11]解答对比Fig.2 Comparison of the results by the present solution with the available solutions of reference[11]

4.2 参数分析

为了分析影响饱和地基扭转动力响应的主要参数及其规律，下面分别探讨简谐扭转荷载的频率与埋深、土体剪切模量非均匀系数及地基土的动力渗透系数等参数对地基扭转动力响应的影响.

以饱和黏性土地基为例[11]，其物理力学参数为：地表处剪切模量μ=9.4×106Pa，孔隙率n=0.4，土颗粒密度ρs=2 650 kg/m3，水的密度ρw=1 000 kg/m3.算例中计算得到的应力、位移皆取幅值并除以k 即τzθ/k、uθ/k 以消除比例系数对结果的影响.

4.2.1 简谐扭转荷载无量纲频率f 的影响

为探讨简谐扭转荷载无量纲频率f 的影响，分别 取 f 为 1.00、1.25、1.50、1.75、2.00、2.25、2.50 及2.75，荷载作用半径a=1 m，埋深h=1，土体剪切模量非均匀系数α=1，土体动力渗透系数kd=10-7m/s，根据编制的计算程序分别计算深度z1=0.5 与z2=1.5 处土体的剪应力以及切向位移，获得如图3、图4所示的土体切向位移、剪应力随无量纲半径的变化曲线.

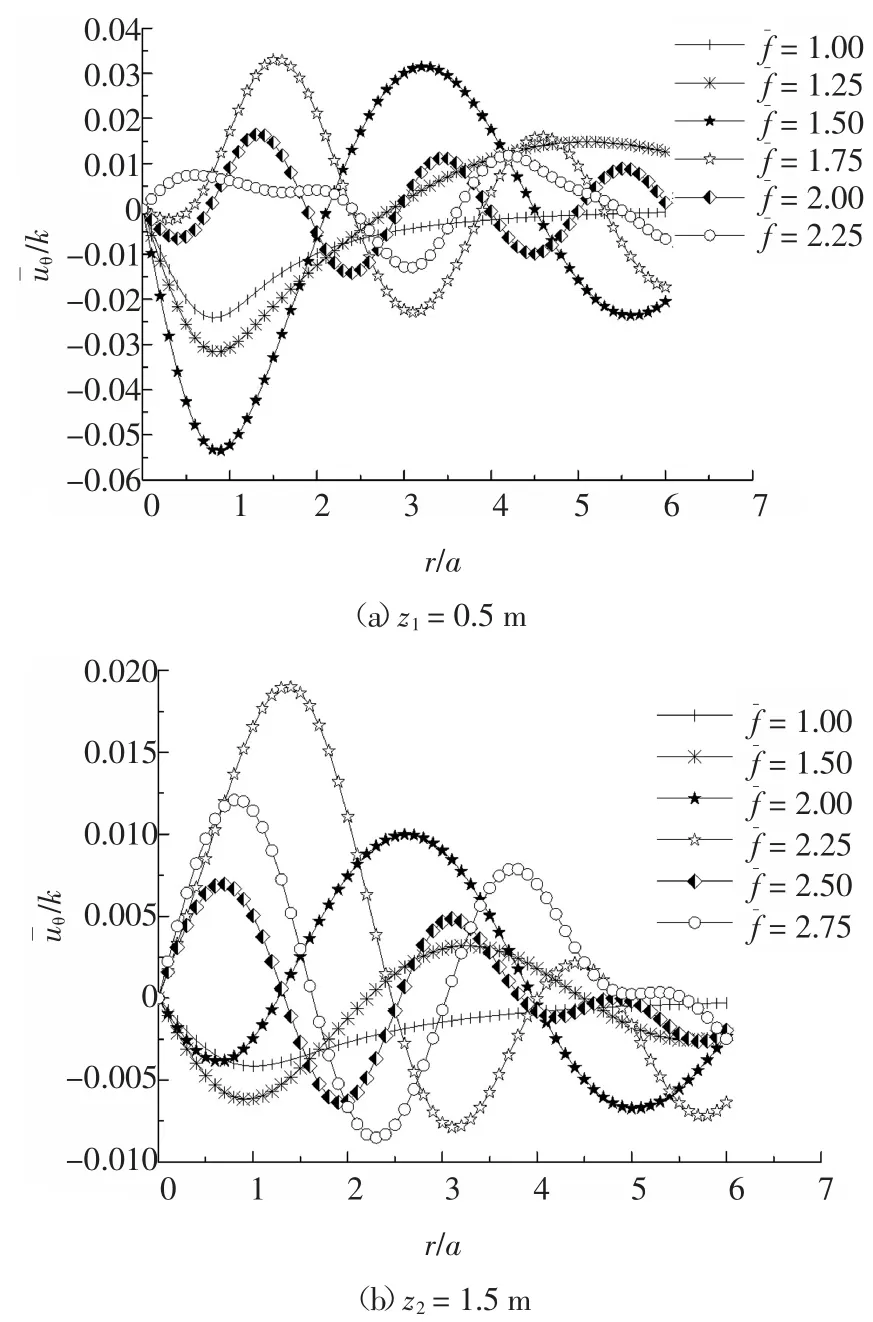
图3 简谐扭转荷载频率对饱和地基切向位移的影响Fig.3 Effect of loading frequency on tangential displacement of saturated soil

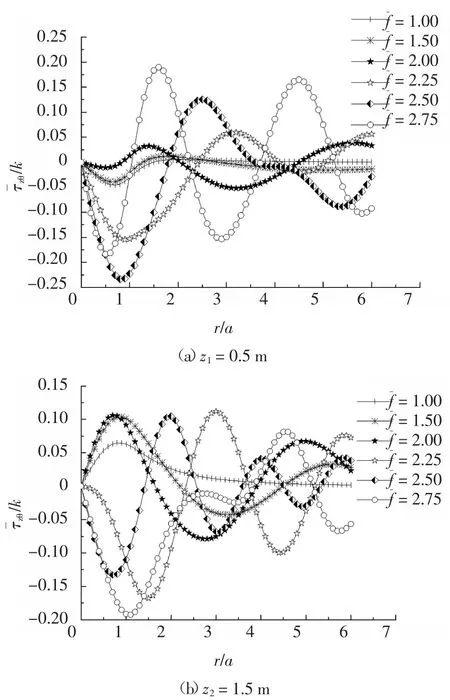
图4 简谐扭转荷载频率对饱和地基应力的影响Fig.4 Effect of loading frequency on stress of saturated soil

由图3、图4 可看出：饱和地基土的剪应力与切向位移沿径向呈现出明显的波动变化规律，随着简谐扭转荷载无量纲频率f 的增大，曲线波动频率逐渐增大. 地基土的切向位移幅值随荷载频率的增大先增后减，即存在某一临界荷载频率，使得切向位移幅值最大，与共振理论相一致.总体趋势上，地基土的应力幅值随荷载频率的增大而增大. 在同一深度处，当r ＞a 时，地基土的应力、位移幅值随着到荷载中心距离的增大而减小，与地基中应力波传播时能量逐渐降低的规律一致.

4.2.2 简谐扭转荷载埋深h 的影响

为探讨简谐扭转荷载埋深的影响，分别取h 为0.5、1.0、2.0 及4.0，荷载频率f=1，其余参数同上，根据所编制的计算程序分别计算r ＞a 处土体不同深度处的剪应力和切向位移，获得如图5、图6 所示的地基土切向位移、剪应力随深度变化曲线.

由图5、图6 可看出：荷载作用面以上，土的剪应力、切向位移随荷载埋深h 的增大而增大，荷载作用面以下，土体的剪应力与切向位移随荷载埋深h 的增大而减小，荷载作用面土体的剪应力发生突变，切向位移达到峰值.当≥2a 时，土体的剪应力、切向位移近似为零，说明埋置荷载主要影响其作用面上、下各两倍荷载作用半径（2a）区域.

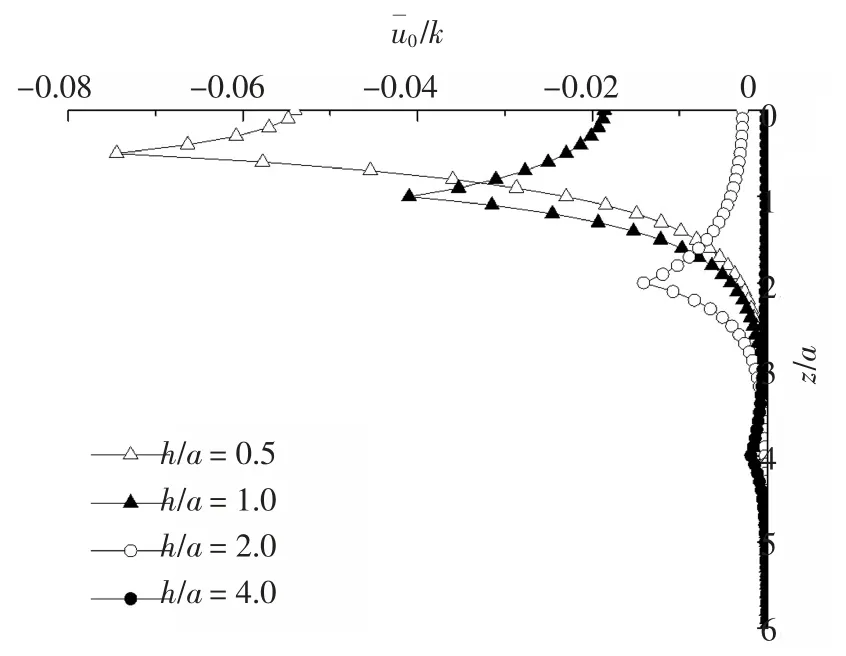
图5 h 对饱和地基切向位移的影响Fig.5 Effect of h on tangential displacement of saturated soil

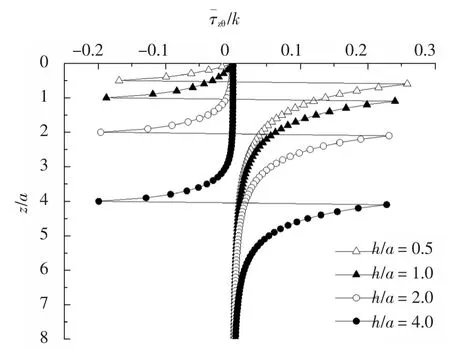
图6 h 对饱和地基应力的影响Fig.6 Effect of h on stress of saturated soil

根据所编制的程序分别计算荷载频率f 为0.1、0.5、1.0 及1.5 时，土体不同深度处的剪应力与切向位移，获得如图7 所示的土体最大切向位移与荷载埋深h 之间的关系曲线.

图7 h 对饱和地基最大切向位移的影响Fig.7 Effect of h on the largest tangential displacement of saturated soil

由图7 可看出：土的最大切向位移随荷载埋深h的增大而减小，荷载埋深小于两倍荷载作用半径（2a）时，曲线急剧下降，h=a 时最大切向位移下降75%，h=2a 时最大切向位移下降90%，h ＞4a 时，饱和地基土的最大切向位移近似为零.

4.2.3 剪切模量非均匀系数α 的影响

为探讨地基土剪切模量分布形式的影响，分别取剪切模量指数函数式（1）中的非均匀系数α 为0.1、0.5、1.0 及1.5，荷载频率f = 1，埋深h = 1，其余参数同上，计算获得如图8、图9 所示深度z1=0.5 处地基土的剪应力、切向位移随半径的分布曲线.

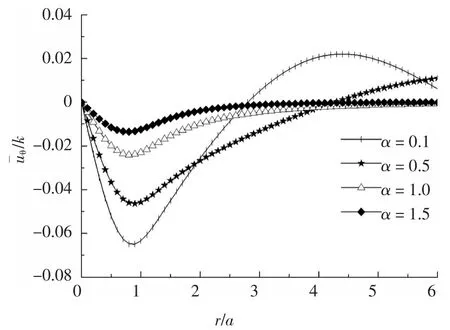
图8 α 对饱和地基切向位移的影响Fig.8 Effect of α on tangential displacement of saturated soil

图9 α 对饱和地基应力的影响Fig.9 Effect of α on stress of saturated soil

由图8、图9 可看出：随地基土剪切模量非均匀系数α 的增大，土中剪应力、切向位移逐渐减小，系数α 每增加0.5 个单位，剪应力峰值下降约23%，切向位移峰值下降约40%，这是因为系数α 越小，地基土越接近均质状态，其变形越大，说明相同荷载条件下，剪切模量随深度呈指数函数分布的非均质地基比均质地基变形小.

4.2.4 地基土动力渗透系数kd的影响

为探讨饱和地基土动力渗透系数的影响，分别取kd为10-2m/s、10-5m/s 及10-7m/s，α=1，荷载频率f=1，埋深h=1，其余参数同上，计算z1=0.5 处土体的切向位移，获得如图10 所示地基土切向位移与无量纲半径的变化曲线.

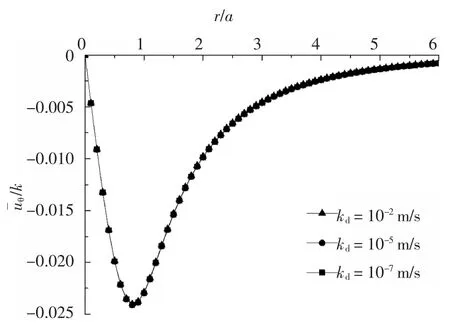
图10 kd 对饱和地基切向位移的影响Fig.10 Effect of kd on the tangential displacement of saturated soil

由图10 可看出：土体动力渗透系数kd的变化对地基土的切向位移几乎没有影响.

5 结 论

假定土体剪切模量随深度呈指数函数非线性分布，基于Biot 固结理论与动力学原理，建立竖向非均质饱和地基内部作用简谐扭转荷载时的动力微分方程，通过Hankel 变换与逆变换求得土体的剪应力与切向位移解答，据此基于Mathematica 编制出相应计算程序，通过参数分析获得土体参数对地基扭转动力响应的影响规律，主要结论如下：

1）埋置简谐扭转荷载作用下，土体的剪应力、切向位移均沿径向呈现出明显波动规律，波动频率随荷载频率的增大而增大，切向位移幅值随荷载频率的增大先增后减，即存在某一临界荷载频率，使得切向位移幅值最大.

2）对比分析表明，随着土体剪切模量指数分布函数中非均匀系数α 增大，土体的剪应力、切向位移逐渐减小，系数α 每增大0.5 个单位，剪应力峰值下降约23%，切向位移峰值下降约40%，说明相同荷载条件下，剪切模量随深度呈指数函数分布的非均质地基比均质地基变形小.

3）埋置简谐扭转荷载作用下，土体的切向位移自地面开始沿深度表现为先增加后减小的变化趋势，荷载作用面处，土的切向位移最大，剪应力发生突变，荷载主要影响范围为其作用面上、下各两倍荷载作用半径（2a），且随荷载埋深h 的增大，土体最大切向位移逐渐减小，h = a 时最大切向位移值下降75%，h = 2a 时最大切向位移值下降约90%，h ＞4a时最大切向位移值近似为零.

4）地基土动力渗透系数kd的变化对土体应力以及切向位移几乎没有影响.

诚然，上述解答暂仅针对竖向非均质（土体剪切模量随深度呈指数函数非线性分布）饱和地基中埋置简谐扭转荷载的动力响应问题，对于地基为非饱和、双向非均质或分层等更为复杂的情况，有待进一步的深入研究.