基于矩阵方法的Banzhaf值的计算及应用

夏美霞,李海涛,丁雪莹,刘衍胜

(山东师范大学数学与统计学院,山东济南 250014)

1 引言

合作博弈描述了有限的一组玩家N可以通过合作产生一定的收益.在合作博弈中,单点解是为每个合作博弈分配一个n维的实向量的函数,这个实向量表示玩家的收益分布.在过去的几十年,对合作博弈中单点解的研究引起了国内外很多学者的研究兴趣.其中,Shapley值和Banzhaf值是最著名的单点解.Shapley值是由Shapley[1]在1953年首次提出.Banzhaf指数最初由Penrose[2]于1946年引入,后来由Banzhaf[3]于1965年引入投票博弈.在此背景下,Banzhaf指数被推广为所有合作博弈的Banzhaf值[4].这两种单点解将不同的权重与每个联盟1联盟[5]:设N={1,2,···,n},N中的任意一个非空子集K称为一个联盟,空集∅为一个特殊的联盟,因此n个玩家可以形成2n个联盟.联系起来,它们分配给每个玩家的收益都是玩家所属的任何联盟的边际贡献2边际贡献[5]:合作博弈中,对∀i∈N和满足i∈K的每个联盟K ∈2N,i对联盟的边际贡献为i=v(K)−v(K{i}).的平均值.Shapley值给出了每个玩家在随机排序中形成大联盟的预期边际贡献[6–7].Banzhaf值提供了每个参与者形成大联盟的预期边际贡献,其中每个联盟以相同的概率形成.Dubey和Shapley[8]证明了Banzhaf值的一些数学性质.

最近,程代展教授等[9]提出了矩阵半张量积方法(semi-tensor product of matrices),并使用这种方法来研究有限静态博弈和有限演化博弈的建模、分析与控制.矩阵半张量积方法的主要特征是将策略局势转换成逻辑变量,这有利于有限博弈的线性表示.在过去10年,国内外很多学者使用这种方法研究有限博弈,建立了很多优秀的研究结果[10–14].文献[10]提出了一种用于网络演化博弈的建模、分析和控制的矩阵方法.文献[12]提出了一种具有多面体策略集的线性动态博弈.此外矩阵半张量积方法也被应用于布尔网络[15–21]、布尔控制网络[22–29]、自动机理论[30–31]和移位寄存器[32]等问题的研究.关于矩阵半张量积方法的综述,参见文献[33–37].

目前Banzhaf值已经在不同场景中得到了广泛应用,包括联盟结构[38–40]、通信情况[41]、层次关系[42]和邻近关系[43]等.Parmigiani等[44]利用微阵列技术以产生大量关于人类基因表达的信息,这些数据可用于鉴定导致特定疾病的基因,从基因表达数据的矩阵推断基因的相互作用以及当生物系统的状况发生变化时它们的行为.Moretti等[45]提出了一种基于联盟博弈的基因表达分析的替代方法.该方法的主要优点是可以计算称为相关性指数的数值指数,该指数可以反应特定疾病中每个基因的相关性.需要指出的是,目前关于Banzhaf值的计算主要是直接基于定义的求解,因此很难使用计算机进行辅助求解.

本文利用矩阵半张量积方法研究Banzhaf值计算问题,并将所得结果应用于生物网络中的遗传疾病基因的相关性研究中.本文的主要贡献是利用矩阵半张量积方法将Banzhaf值转化成等价的代数形式,并建立了一个简捷的计算方法.相较于定义中直接计算的方法,本文给出的方法便于使用计算机进行辅助求解,并且适用于求解任意有限合作博弈的Banzhaf值.由于使用定义计算Banzhaf值与根据本文提出的方法计算Banzhaf值所需的计算量复杂度均为O(n2n),所以本文用一台配置为因特尔酷睿i7–6500U 2.5 GHz CPU的电脑进行MATLAB数值仿真时,当玩家数超过15时就无法运行了.数值仿真表明,在MATLAB容许的玩家数范围内,与定义相比,本文给出的计算Banzhaf值的方法所需要的MATLAB运行时间更短.

本文的剩余部分安排如下:第2节列出了矩阵半张量积的一些必要的预备知识;第3节给出Banzhaf值的等价代数形式和计算方法;第4节将得到的结果应用于生物遗传疾病基因的相关性度量;第5节给出本文的结论.

下面给出本文中用到的符号:R表示实数;1p=为所有p×q维逻辑矩阵的集合,···,p},其中表示单位矩阵Ip的第i列;一个n×t维逻辑矩阵M=可以简记为M=δn·[i1i2···it];Coli(M)表示矩阵M的第i列,Col(M)表示了矩阵M的所有列组成的集合,设M则M ∗N:=[Col1(M)⊗Col1(N)···Colr(M)⊗Colr(N)],其中⊗表示矩阵的Kronecker积.

2 预备知识

本文使用的主要数学工具为矩阵半张量积,定义如下所示.

定义1[9]给定两个矩阵矩阵M和N的半张量积定义为

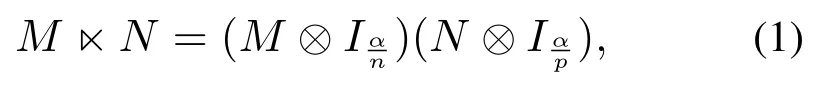
其中α为n和p的最小公倍数.

注1矩阵半张量积是普通矩阵乘积的推广,因此一般省略符号“”.

下面给出换位矩阵的定义:

定义2[9]换位矩阵W[m,n]∈Lmn×mn定义为

引理1[9]设X为两个列向量,则有W[m,n]XY=Y X.

引理2[9]设f:Dn→D为一个逻辑映射.则存在唯一的逻辑矩阵Mf∈L2×2n使得

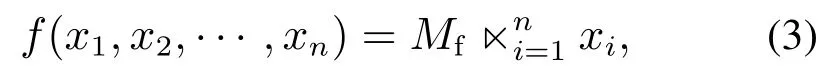
其中Mf称为f的结构矩阵.

定义3[35](有限)正规博弈G=(N,S,C)由3部分构成,其中N={1,2,···,n}表示有n个玩家,S=称为局势,Si为第i个玩家的策略集,C={c1,···,cn},ci:S→为第i个玩家的收益函数.

定义4[35]一个带有可转移效用3可转移效用[5]:各个玩家都用相同的尺度来衡量他们的收益,并且各个联盟的收益都可以用任何方式分配给各玩家.(transferable utility,TU)的n人合作博弈可由二元结构(N,v)表示,其中:N={1,2,···,n}是玩家集,v:2N→为特征函数4特征函数[5]:给定N={1,2,···,n},n人合作博弈的特征函数v是从2N={K|K ⊆N}到实数集的映射.,满足v(∅)=0.

3 主要结果

本节给出Banzhaf值的等价代数形式和计算方法.首先回顾Banzhaf值的定义.

设K ⊆N,则K是一个联盟,v(K)表示合作博弈中联盟K的收益.记

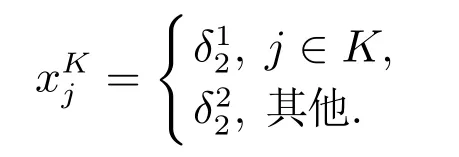
则由式(3),可以找到v的结构向量Mv使得

其中Mv∈

为了方便下面的计算与应用,这里先定义一个无异议博弈.

定义5[46]一个在R⊆N上的无异议博弈(N,uR)定义为

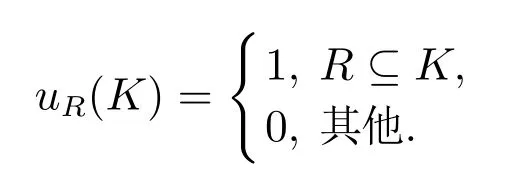
Banzhaf 值提供了每个参与者形成大联盟的预期边际贡献,其中每个联盟以相同的概率形成.下面给出Banzhaf值的定义.

定义6[4]给定合作博弈(N,v),其Banzhaf值β是一个定义在Rn上的向量:

其中:

其中i=1,2,···,n.

下面使用矩阵半张量积方法研究式(5),给出Banzhaf值的等价代数形式和计算方法.

由式(4)和换位矩阵的性质可得

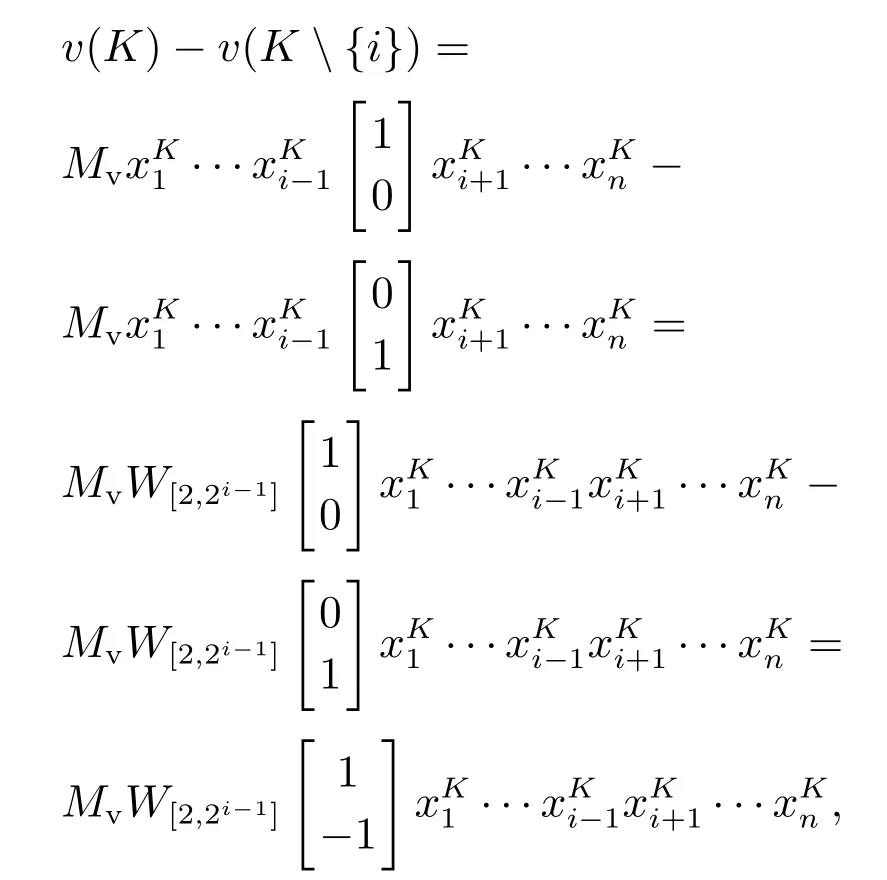
其中Mv是v的结构向量.

由于对任意的l=1,···,n,即l∈K时,本文令

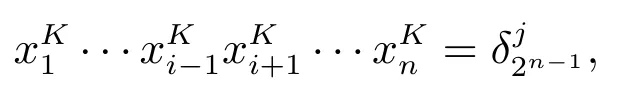
其中j ∈{1,2,···,2n−1}.则对于任意的i=1,2,···,n,式(5)可表示为

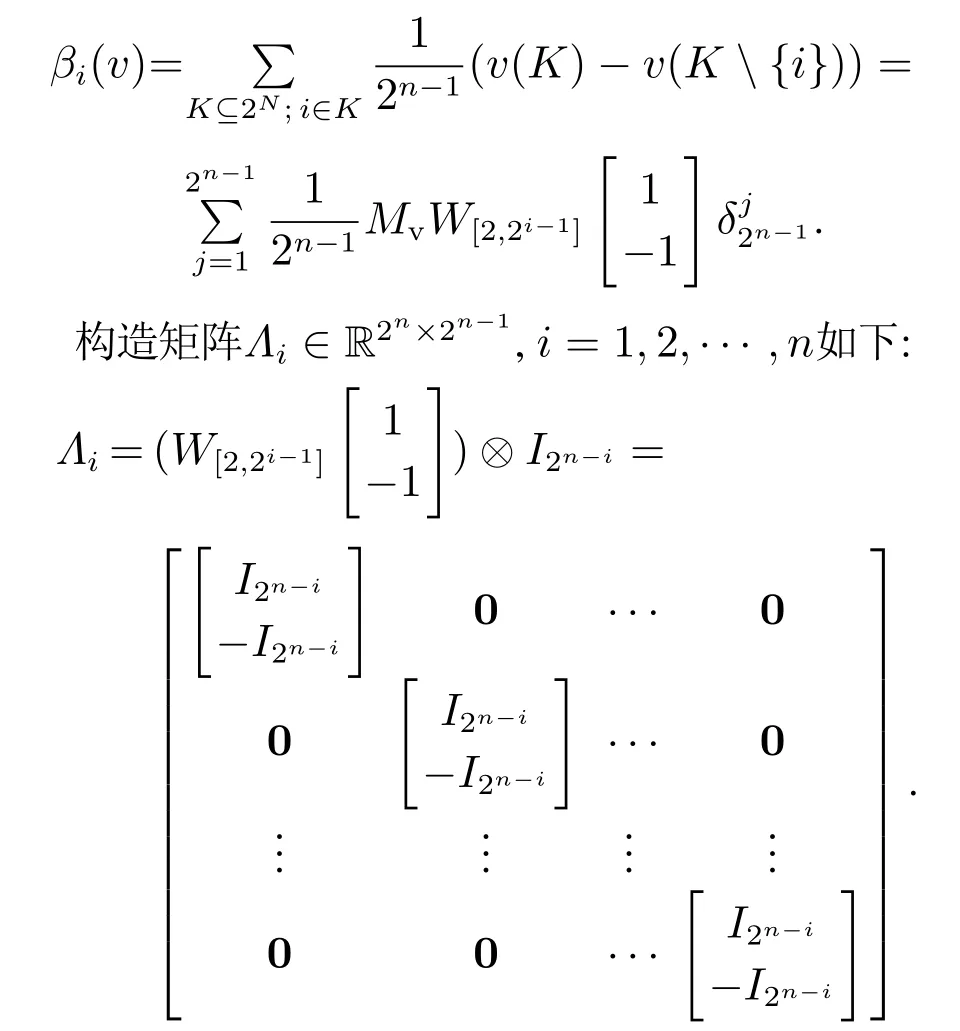
其中0表示2n−i+1×2n−i维零矩阵.

容易得出

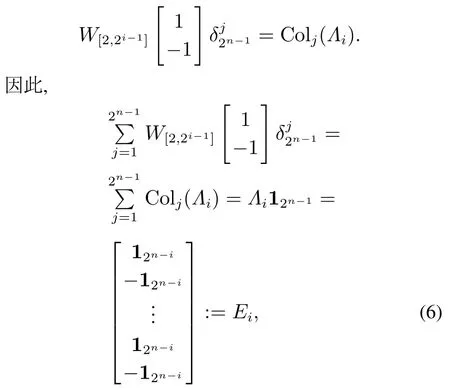
这里Ei是一个2n维列向量,i=1,2,···,n.

因此式(5)可重新表示为下式

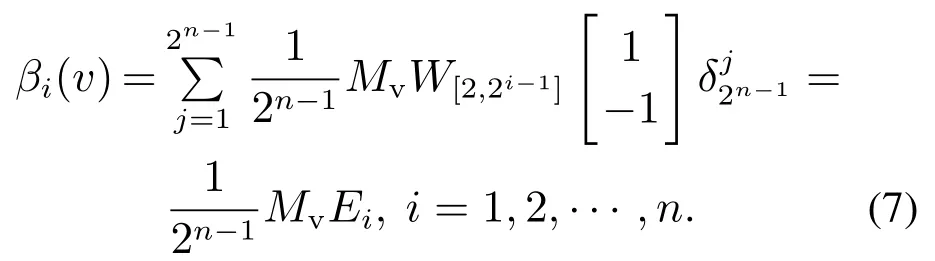
基于以上分析,得到如下计算Banzhaf值的代数表示办法.

定理1给定合作博弈(N,v),其中:N={1,···,n},Mv是v的结构矩阵.则该合作博弈的Banzhaf值可计算如下:

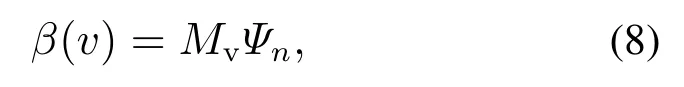
其中

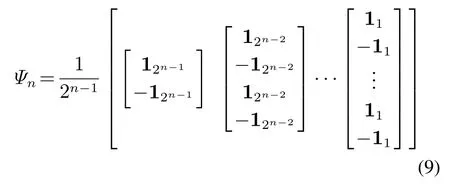
是一个2n×n维矩阵.

证由于该合作博弈的Banzhaf值为

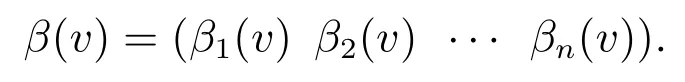
由式(7)可得

又通过式(6),可以计算出

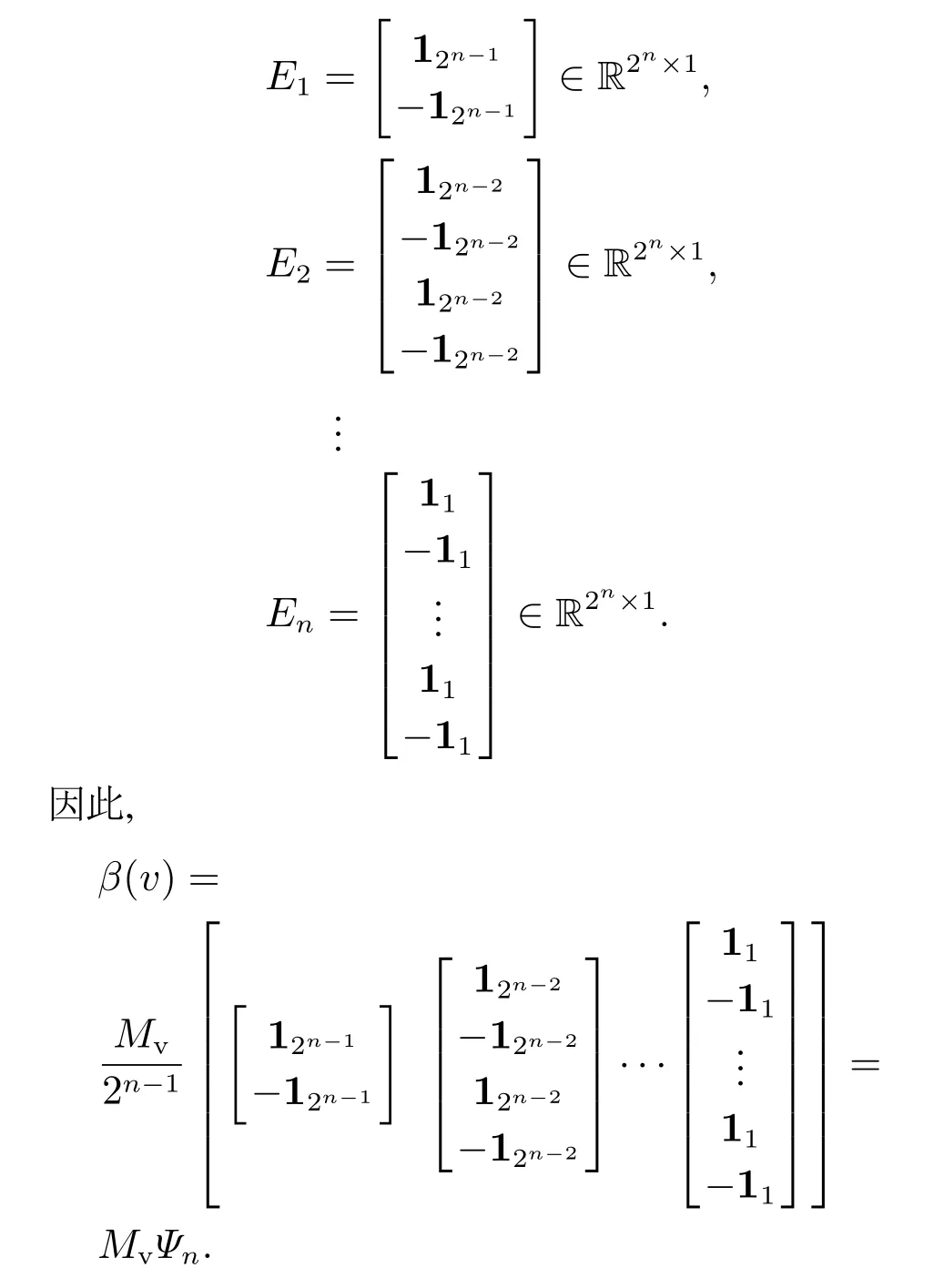
证毕.

例1考虑一个合作博弈(N,v),其中N={1,2,3},特征函数的结构矩阵如下:

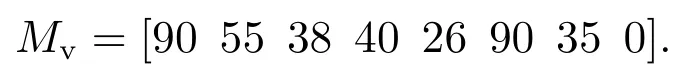
由式(9)可以得到式(10),因此可以计算出这个合作博弈的Banzhaf值为β(v)=MvΨ3=[18 37 1].

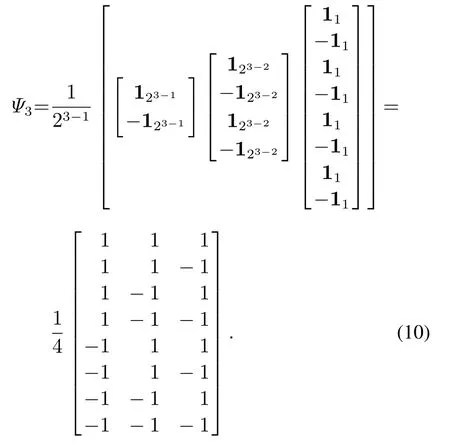
因此,可以计算出这个合作博弈的Banzhaf值为

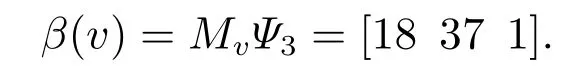
例2考虑手套市场博弈[47].假设玩家集合N={1,···,n}可分为两个互不相交的子集L和R.L中的玩家每个人有一只左手套,R中的玩家每个人有一只右手套.左右手套两只搭配起来可以产生价值1美元,而单独一只手套没有任何价值.本文可以用n人合作博弈(N,v)来表示这个问题:v(K)=min{|L ∩K|,|R ∩K|},∀K ∈2N.

假设

当n=5时,L={1,2,5},R={3,4};

当n=6时,L={2,3,5},R={1,4,6};

当n=7时,L={2,6},R={1,3,4,5,7};

当n=8时,L={1,2,3},R={4,5,6,7,8};

当n=9时,L={1,4,5,6},R={2,3,7,8,9};

当n=10时,L={2,3,5,6,8,9,10},R={1,4,7};

当n=11时,L={2,4,6,7,9,10,11},R={1,3,5,8};

当n=12时,

L={2,6,7,9,10,11},R={1,3,4,5,8,12};

当n=13时,

L={1,2,4,6,7,9,10,11},R={3,5,8,12,13};

当n=14时,

L={2,4,6,7,9,10,11,14},R={1,3,5,8,12,13}.

本文用一台配置为因特尔酷睿i7–6500U 2.5 GHz CPU的电脑进行MATLAB数值仿真,对不同的n分别用定义6和定理1计算Banzhaf值,并得出所用的运行时间,见表1.表中方法1是用定义6直接计算,方法2是用定理1提出的代数表示计算的,而最后一列就是得出的Banzhaf值.当n15时,使用该配置的电脑在这两种方法下都无法再进行MATLAB数值仿真.

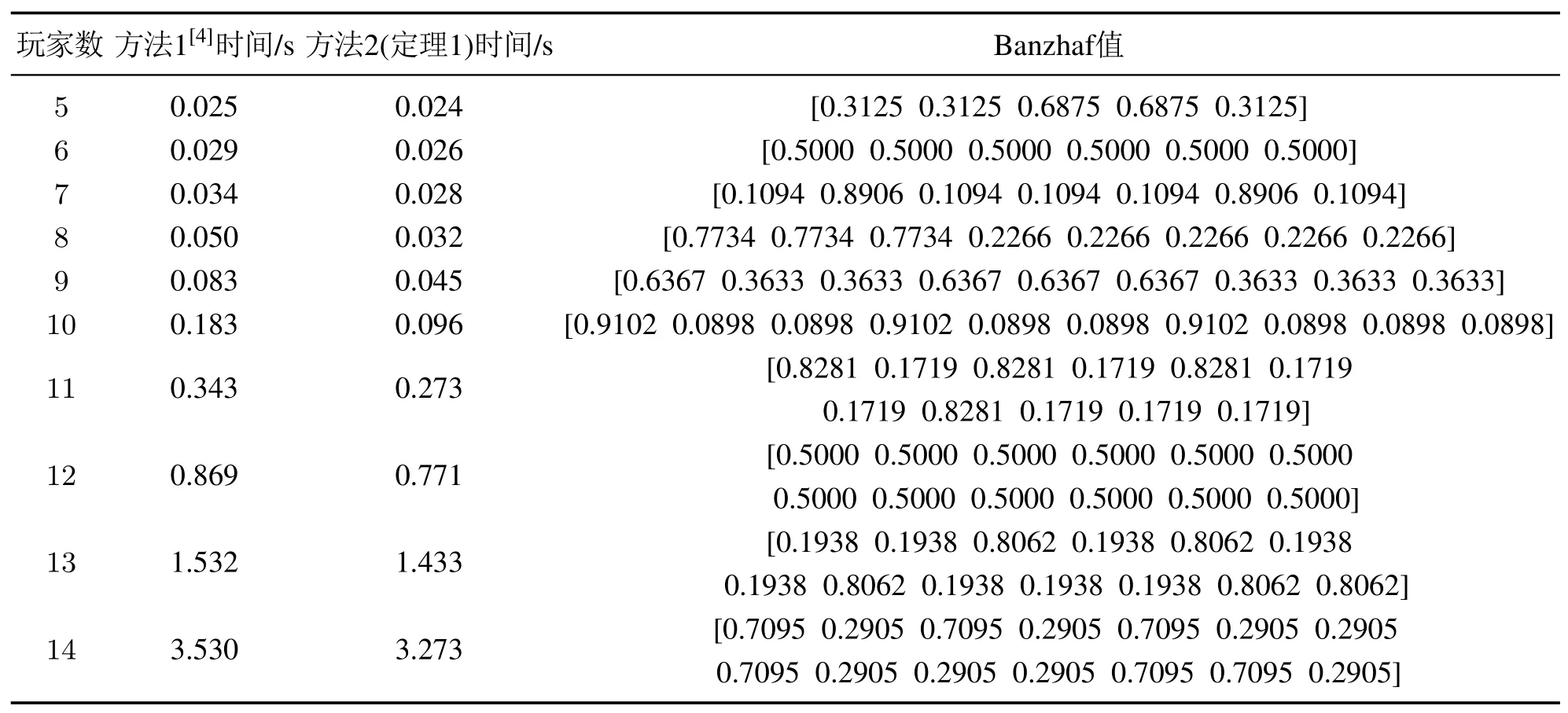
表1 不同玩家数下计算Banzhaf值的两种方法所用MATLAB运行时间比较Table 1 Comparisons of the running time of MATLAB for two methods of calculating Banzhaf value under different number of players

注2经过分析作者发现,根据定义6计算Banzhaf值与根据本文提出的定理1计算Banzhaf 值所需的计算量复杂度均为O(n2n).但是,本文建立的代数表示方法在形式上对Banzhaf值的计算更加简洁.并且由于定理1提出的代数表示方法将子集的信息存储在矩阵Ψn中,所以通过表1可以看出,与定义6相比,定理1计算Banzhaf值所需要的MATLAB运行时间更短.

4 应用

生命活动中,基因表达发生改变是一种常见的现象,也是生物学研究的核心问题.通过对基因差异表达的研究,可以推断细胞分化中基因“开启”或“关闭”的机制,揭示基因与疾病的发生,发展,转归的内在联系.近年来,一种称为微阵列技术的新的研究方法被提出[44],利用该技术可以产生大量关于人类基因表达的信息,可用于鉴定导致特定疾病的基因.然后通过某种判别方法,将基因表达信息转化为一个布尔表达矩阵,称之为微阵列矩阵,利用该矩阵推断基因的相互作用以及当生物系统的状况发生变化时它们的行为.

N={1,2,···,n}是n个基因的集合.是来自正常组织的一组细胞集合,是具有遗传疾病的组织的细胞集合.Aij ∈表示在样本j(j ∈SR∪SD)中基因i的表达值.SR和SD中样本的表达矩阵分别定义为微阵列实验情况(microarray experiment situation,MES)可表示为一个5元组E=实验的目的是将样本与表达局势相关联,并根据某个判别方法m来判断SD中样本的基因关于SR中样本的表达值是否出现异常.本文用“1”表示异常表达的基因,用“0”表示正常表达的基因.使用这个判别方法m可以得出相应的布尔表达矩阵即微阵列矩阵,记为M.

给定一个微阵列矩阵M=(mij).对于M的一个列m·j,j=1,···,d,定义了它的支撑为(m·j)={i:mij=1}.注意到对微阵列矩阵的每一列j,至少存在一个i使得mij≠0.

为了反映特定疾病中每个基因的相关性,Moretti等[45]提出了一种基于联盟博弈的基因表达分析的替代方法,利用该方法计算称为相关性指数的数值指数.Banzhaf值作为合作博弈的一个单点解,提供了每个参与者形成大联盟的预期边际贡献.基于此,Lucchetti等[46]提出了使用Banzhaf值来度量基因相关性的方法.但是该文中Banzhaf值的计算是直接基于定义的求解,很难使用计算机进行辅助求解.下面本文将得到的Banzhaf值的计算方法应用于生物遗传疾病基因的相关性度量.

例3给定一个n=4的微阵列实验情况和判别方法m,它对应的微阵列矩阵为

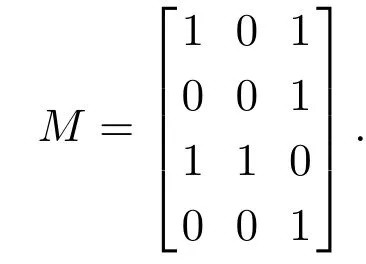
下面用Banzhaf值度量基因与肿瘤发作的相关性.

显然M的列对应的支撑分别为(m·1)={1,3},(m·2)={3},(m·3)={1,2,4}.

由于微阵列博弈的特征函数v是根据基因组的充分性原则,为每个联盟K ∈2N分配由K确定的肿瘤样本的平均数,计算的等价方法是如下无异议博弈的和:

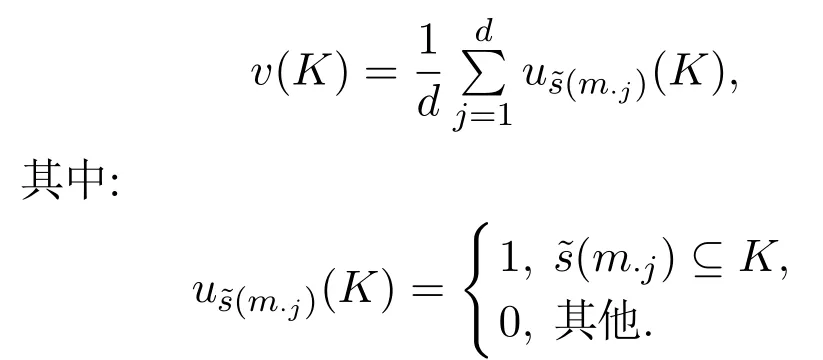
于是M对应的v(K)计算为

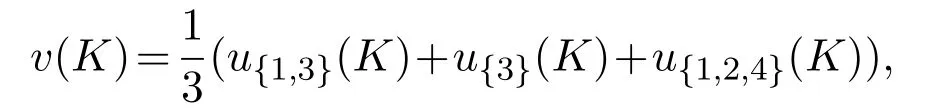
因此可以得到

从而可得v的结构矩阵为

由式(9)可以得到

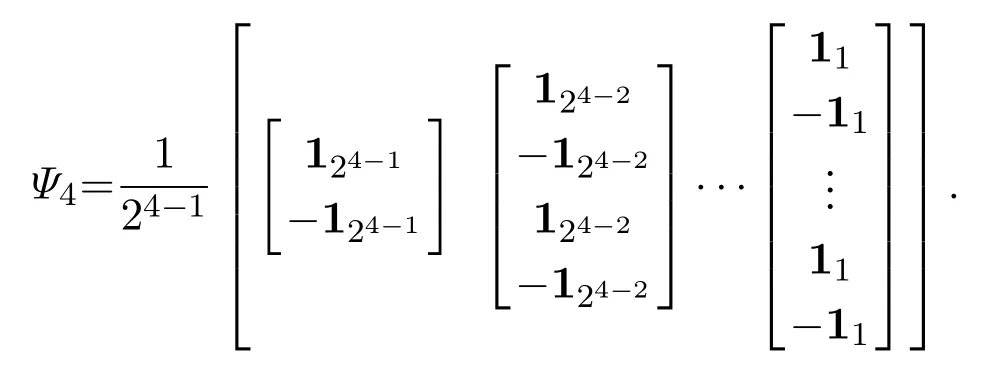
由定理1,可以计算出这个合作博弈的Banzhaf值为

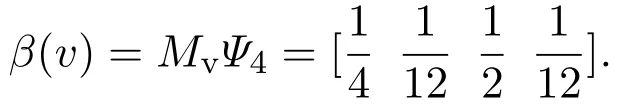
因此可以得到确定肿瘤发作的最重要的基因是基因3,其次是基因1,最后是基因2和基因4.

5 结论

本文研究了合作博弈的Banzhaf值的求解问题.利用矩阵半张量积方法,给出了合作博弈特征函数的代数表示,基于此给出了Banzhaf值的等价代数形式和计算方法.本文还将所得结果应用于生物网络中遗传疾病基因的相关性问题中,利用Banzhaf值度量与疾病发作高度相关的基因.

由于使用定义6计算Banzhaf值与根据本文提出的定理1计算Banzhaf值所需的计算量复杂度均为O(n2n),所以本文用一台配置为因特尔酷睿i7–6500 U 2.5 GHz CPU的电脑进行MATLAB数值仿真时,当玩家数超过15时就无法运行了.数值仿真表明,与定义6相比,定理1计算Banzhaf值所需要的MATLAB运行时间更短.