滑动与打滑条件下的轮式移动机器人自抗扰跟踪控制

王立玲,董力元,马 东,刘秀玲,王洪瑞

(河北大学电子信息工程学院,河北保定 071002;河北省数字医疗工程重点实验室,河北保定 071002)

1 引言

近年来轮式移动机器人在军事民用工程领域发挥着越来越多的作用,如扫雷、侦察、医院任务、物流搬运等,其轨迹跟踪控制问题引起了很多国内外学者的关注.目前,解决轮式移动机器人轨迹跟踪问题的方法主要有反步法控制[1–2]、滑模控制[3–4]、自适应控制[5–6]、神经网络控制[7–8]等.

在上述文献中,都假设轮式移动机器人满足“理想的非完整约束”条件.即,机器人在运动中始终保持“纯滚动无滑动”状态.然而,轮式移动机器人工作环境是十分复杂的.由于冬天道路结冰,雨天道路潮湿或者快速转弯等情况,轮式移动机器人就可能发生侧向滑动和纵向打滑,破坏了机器人的理想非完整约束.因此,研究滑动与打滑下的轮式移动机器人的轨迹跟踪控制很有意义.

目前对满足理想的非完整约束的轮式移动机器人动力学建模研究比较广泛,但对其在滑动与打滑条件下的建模研究相对缺乏.首先Wang等建立了具有滑动与打滑的轮式移动机器人运动学模型,并验证了其打滑下轨迹跟踪的可控性和可操作性[9].Kang和Chen等依据滑动与打滑下的轮式移动机器人动力模型,分别提出了一种基于广义扩展状态观测器[10]的鲁棒跟踪控制器[11]和基于扰动观测器的鲁棒跟踪控制器[12].Yoo 提出了一种适用于轮式移动机器人在滑动与打滑下的自适应跟踪控制方法,该算法同时考虑到发生滑动和打滑存在的扭矩饱和,但是对机器人动力学系统不确定性的影响考虑不足[13].Cui等基于轮子产生纵向滑动时的移动机器人运动学模型,提出了一种自适应跟踪控制策略,由于没考虑到轮式移动机器不确定性问题,该控制器的鲁棒性不太理想[14].针对含有未知扰动的非线性时变系统,提出了一种基于线性扩展观测器的自抗扰控制方法[15].

本文主要研究了滑动与打滑下的轮式移动机器人(wheeled mobile robots,WMR)轨迹跟踪问题.受到文献[15]的启发,本文设计了一种基于线性扩展观测器的自抗扰动力学控制器.首先建立了WMR在滑动与打滑下的动力学模型,然后利用反步法设计运动学控制器,基于模型设计线性扩张观测器和自抗扰动力学控制器并证明了动力学系统是有界输入有界输出稳定的.最后仿真结果验证了本文控制器具有收敛速度快和鲁棒性强的特点.

2 问题描述

本文以质心与几何中心重合的轮式移动机器人为研究对象,前轮为万向轮,仅起支撑作用,两个后轮为独立驱动.假设OXY为全局坐标系,PoXoYo为局部坐标系.滑动与打滑条件下的WMR模型如图1所示.

图1 轮式移动机器人模型Fig.1 Wheeled mobile robots model

图1中:r为WMR的半径,b为WMR两驱动轮距离的一半,mc为WMR的主体质量;mw为带有电机的WMR驱动轮的质量;Ic为WMR通过的Po关于车轴惯性力矩,Iw为WMR驱动轮关于车轴的惯性力矩,Im为WMR驱动轮关于半径的惯性力矩;ξ为纵向打滑时WMR 驱动轮的角速度扰动向量.

定义轮式移动机器人位姿为q=[x y θ θrθl]T,在滑动与打滑条件下,轮式移动机器人的非完整约束方程为

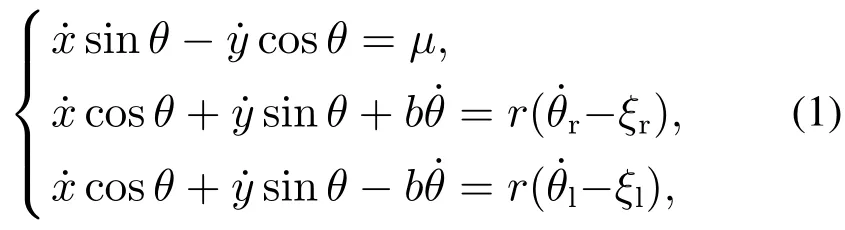
其中:(x,y)为Po在滑动与打滑下全局坐标系的坐标,θ为WMR的方位角,θl和θr分别为左右驱动轮旋转的角度.ξl,ξr和µ分别为WMR左右驱动轮的打滑时角速度扰动和WMR侧向滑动扰动,大小取决于车轮与道路状况等.

为简化非完整约束(1),本文可以用矩阵重写它们如下:

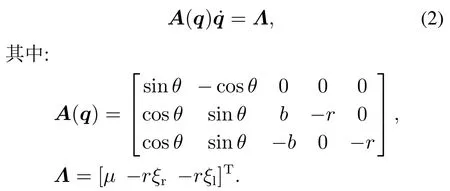
选择一满秩矩阵S(q)为A(q)零空间的一组基,使得A(q)S(q)=0.

在滑动与打滑下的轮式移动机器人的运动学方程可表示为

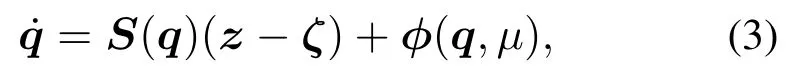
其中:

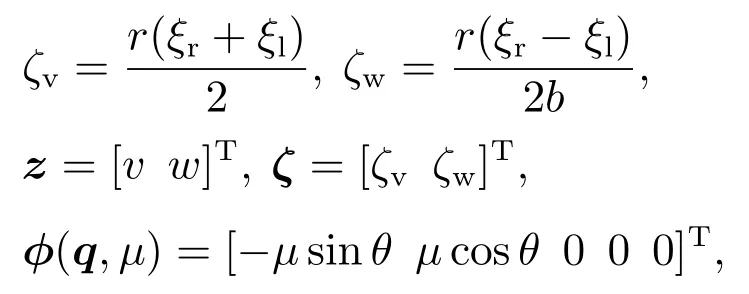
v和w分别为WMR的线速度和角速度,ζv和ζw分别为纵向打滑引起的WMR的纵向打滑扰动和横摆率扰动,ϕ(q,µ)是车轮发生侧向滑动时引起的扰动向量[11].

假设1扰动ζv,ζw,ϕ(q,µ)为连续有界的,它们的一阶导数也是连续有界的,其中:βd2,∥ϕ(q,µ)∥<βd3,βi,βdi,i=1,2,3是未知的正常数.

轮式移动机器人的动力学模型一般可以描述为[13]

考虑到WMR受到滑动与打滑以及外界对自身的干扰的影响,本文应该考虑其动力学模型参数不确定性和未知动力学输入干扰,因此式(5)改写如下:

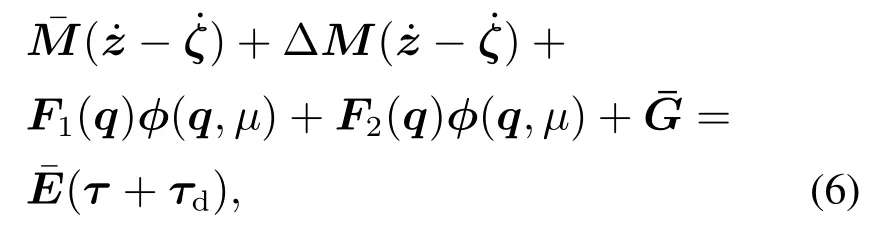
由于假设WMR在水平地面上运行,G(q)=0,重写式(6),如下所示:

定义d为WMR模型不确定性变化量∆(q),未知输入扰动τd和滑动与打滑引起扰动向量ζ和ϕ(q,µ)的集总扰动,且d是有界可导的.

3 反步法运动学控制设计

在轨迹跟踪中,只需知道位姿q中的坐标和方位角,本文重新定义轮式移动机器人位姿为q=[x y θ]T,则有

假设2轮式移动机器人在全局坐标系下的参考轨迹定义如下:

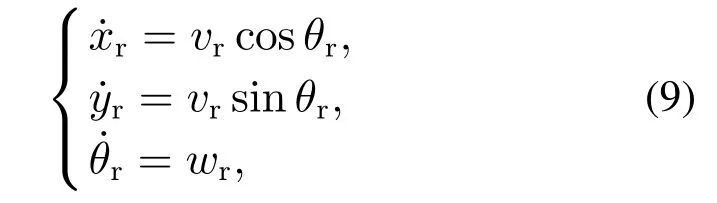
式中vr和wr分别为WMR有界的参考线速度和角速度,且vr>0.

轮式移动机器人位姿跟踪误差的微分方程为

利用反步法,轮式移动机器人运动学控制律为[1]

其中:k1,k2,k3为正常数,vc,wc分别为WMR的虚拟线速度和角速度.

4 自抗扰动力学控制设计

由于轮式移动机器人在滑动与打滑下的动力学特性是十分复杂的,vc和wc往往不是轮式移动机器人真实的线速度和角速度.本文可以将vc和wc视为虚拟速度,基于滑动与打滑的动力学模型,实现轨迹的完美跟踪.

4.1 扩张状态观测器设计

定义状态变量x1=z,x2=d,则系统(7)的状态空间描述为

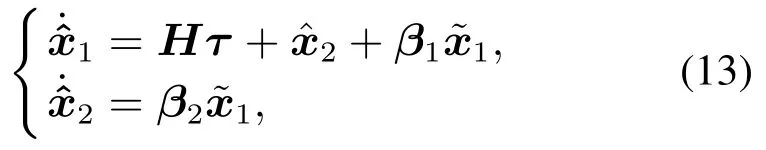
其中由文献[15]可知

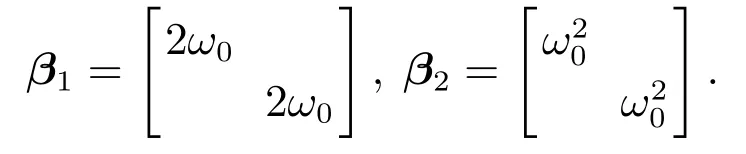
ω0是观测器带宽,ω0>0.

4.2 动力学控制器设计

基于自抗扰的动力学控制器可以分为集总扰动补偿部分和虚拟速度跟踪部分.对集总扰动补偿部分设计如下:

对虚拟速度跟踪部分设计如下:

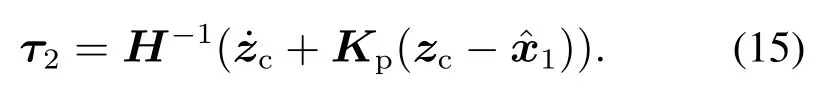
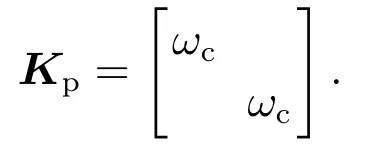
由式(14)–(15)可得动力学控制律为

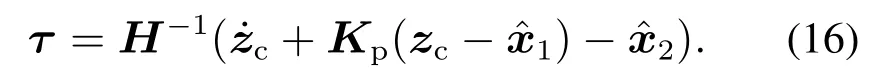
4.3 动力学控制器稳定性分析

定理1在式(17)中,若d中每个元素都是有界可导的,对于任意ω0>0存在一个常向量b=[δ1δ2]T,δi>0,使有限时间内中的每个元素满足δi,其中:i=1,2,j=1,2.

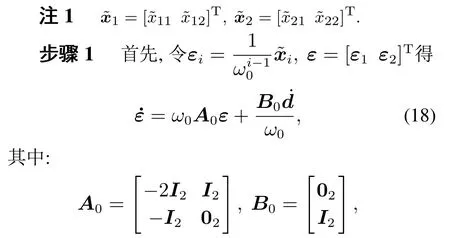
I2表示二阶单位阵,02表示二阶零矩阵.

步骤2设观测器初始误差为零,解方程(18)得到

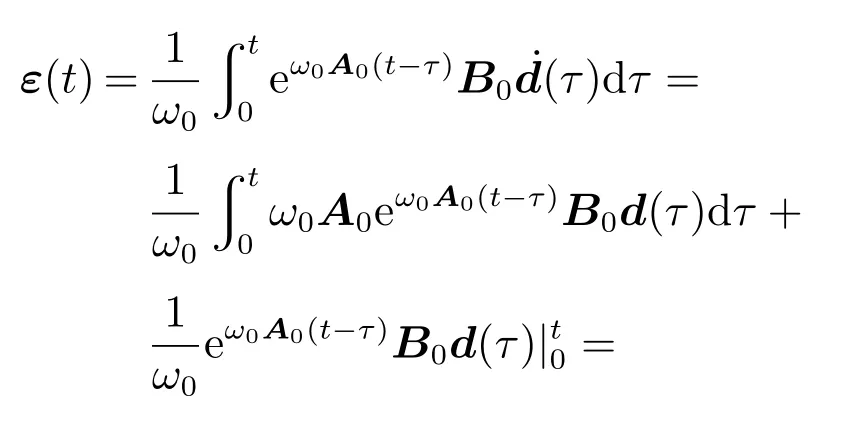
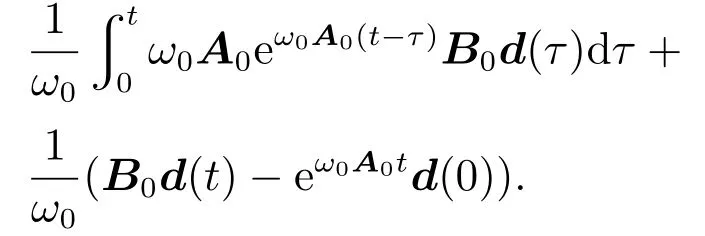
因为d(t)中每个元素都是有界的,即存在一个正常向量dm,满足d(t)dm,因此

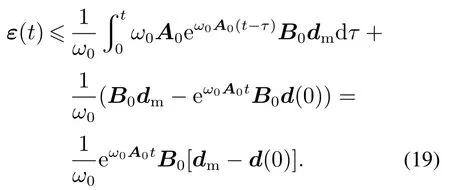
根据文献[15],A0是赫尔维兹矩阵,则存在一个有限时间T1,对所有tT1有

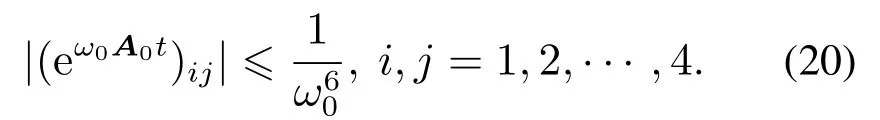
不妨设dm−d(0)=[γ1γ2]T,γ1,γ2为常数,则B0×[dm−d(0)]=[0 0γ1γ2]T,可得

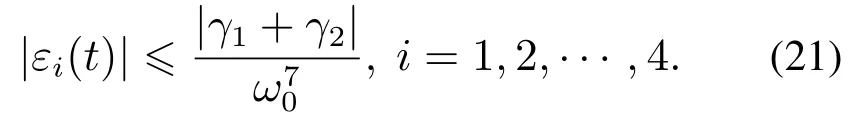
令ε(t)=[ε11ε12ε21ε22]T,重写式(21)如下:

所以扩张状态观测器是稳定的,并且观测器误差与带宽成反比.

下面对动力学系统式(7)进行分析,令速度追踪误差ec=z −zc.

定理2对WMR动力学系统式(7),选择线性扩张状态观测器式(13),自抗扰动力学控制器式(16),若d(t)是有界可导的,则对任意的ω0>0,ωc>0,存在一个常向量ρ=[ρ1ρ2]T,且ρi >0,使得在有限时间内ec中每个元素|(ec)i|ρi,i=1,2.

证由式(7)(13)(16)可得

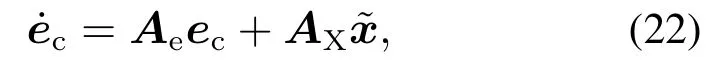
其中:

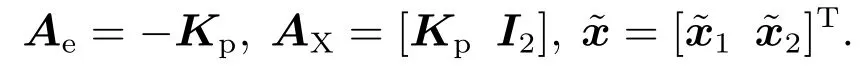
解方程(22)得

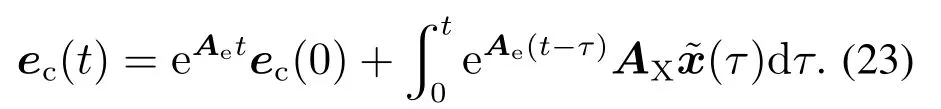
由定理1得,∀tT1,i=1,2,

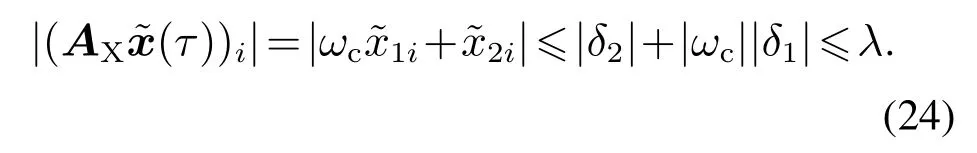
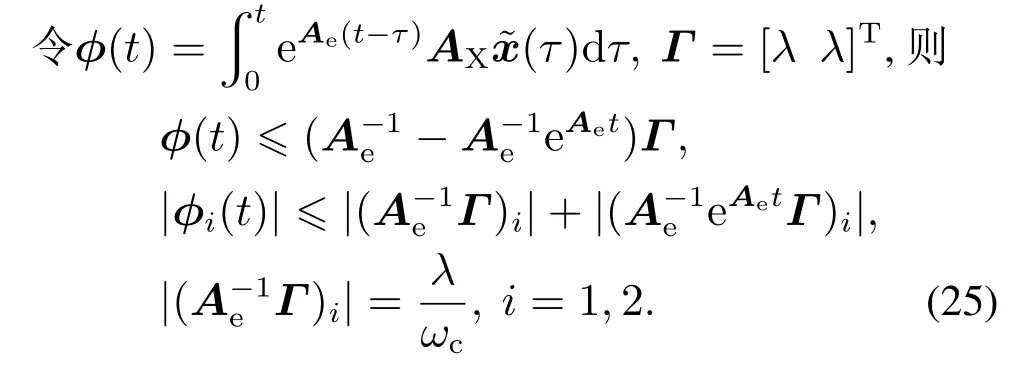
因为Ae为赫尔维兹矩阵[15],则存在一个有限的时间T2,对所有tT2,

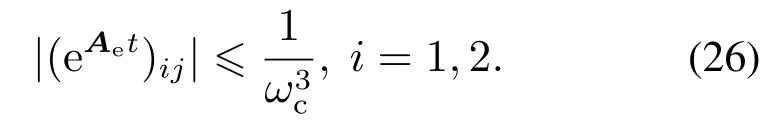
令T=max{T1,T2},对于tT,则

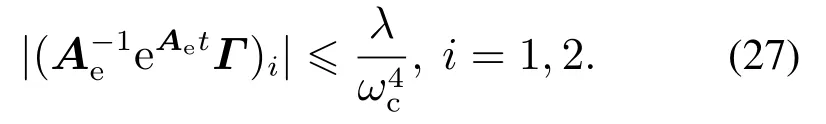
由式(25)(27)可得

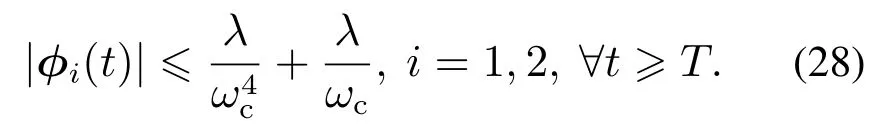
令emax(0)=|[eeec(0)]1|+|[eeec(0)]2|,则

由式(28)–(29)可知,对tT,i=1,2,

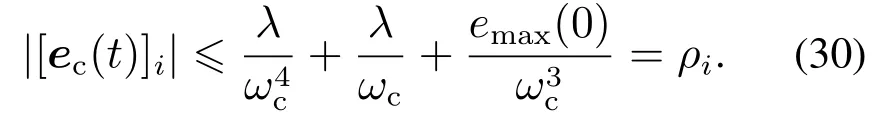
由式(30)可知,速度追踪误差ec是有界的并且随控制器带宽增大而减小,即自抗扰动力学控制系统是稳定的. 证毕.

由上面分析可知,WMR的控制系统原理如图2所示.

图2 WMR的控制系统结构图Fig.2 WMR control system structure diagram

5 仿真

为了验证本文所提出的控制方案的可行性,选择双纽线和圆形两种参考轨迹进行了MATLAB仿真实验.WMR的模型参数:

r=0.05 m,b=0.15 m,mc=3 kg,mw=0.5 kg,

Im=0.00125 kg·m2,Ic=0.0675 kg·m2,

Iw=0.01125 kg·m2.

运动学控制器参数:k1=11.7,k2=11.1,k3=8;自抗扰动力学控制器参数:kp=diag{8,8};线性观测器参数:ω0=40.

1)双扭线轨迹跟踪控制.

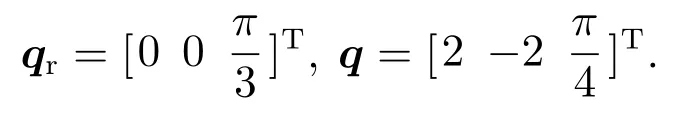
WMR只发生了纵向打滑,驱动轮的角速度扰动分别为ξr=sint+1 rad/s,ξl=0.01t−sin(2t)+2 rad/s.纵向打滑下的WMR轨迹跟踪结果,位姿误差变化及对ξr和ξl的估计值如图3(a)–3(d)所示.

图3 纵向打滑跟踪Fig.3 Tracking under longitudinal sliping

由图3可以看出,WMR能够在纵向打滑条件下跟踪参考轨迹;WMR位姿误差在较短的时间内收敛;线性扩张观测器能够实时地,准确地观测纵向打滑时WMR驱动轮的角速度扰动ξr和ξl.

为进一步验证本文控制器在滑动与打滑情况下的性能,让WMR3∼5 s发生侧向滑动,侧向滑动扰动µ=1 m/s.侧向滑动下的WMR轨迹跟踪结果,位姿误差变化及对集总扰动d的估计值如图4(a)–4(d)所示.

图4 侧向滑动跟踪Fig.4 Tracking under lateral sliding

由图4可以看出,WMR仍能在侧向滑动下跟踪参考轨迹;WMR位姿误差在刚开始迅速地收敛并稳定,当发生侧向滑动时,虽然位姿误差发生了较小波动,但是在本文控制器作用下又迅速地收敛并稳定;线性扩张观测器也能实时地,准确地观测侧向滑动时存在有限个不可导点的集总扰动d.

2)圆形轨迹跟踪控制.

圆形轨迹:xr=5 cos(0.2t),yr=5 sin(0.2t),WMR的初始参考位姿和实际位姿分别qr=为了对所提出控制器鲁棒性做进一步研究,假设轮式移动机器人的未知动力学输入扰动服从正态分布函数:在运行t=8 s时负载发生了缓慢变化:mc=3.3 kg.WMR既发生纵向滑动又发生了侧向滑动,情况如下:

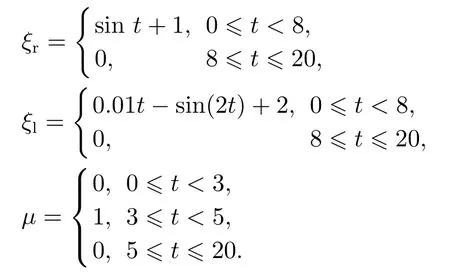
本文采用文中算法和反步法设计运动学控制器与积分滑模控制器结合算法(backstepping kinematic control integral sliding mode control,BKCISMC)进行了仿真对比.BKCISMC算法中运动学控制器与文中算法参数相同,积分滑模控制器中的比例增益,滑模增益大小:Lp=diag{8,8},LD=diag{7,7}.轨迹跟踪对比结果如图5所示.

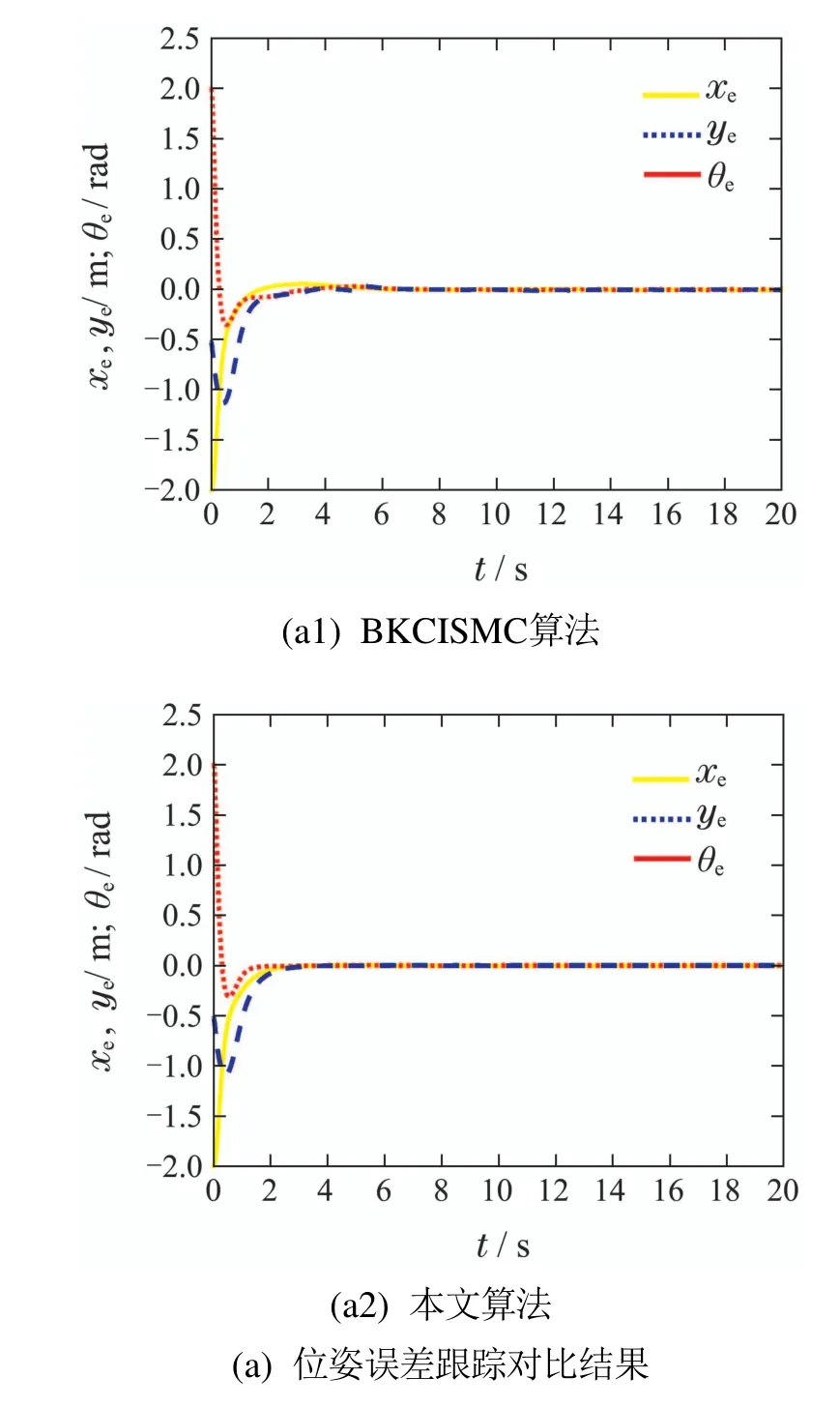
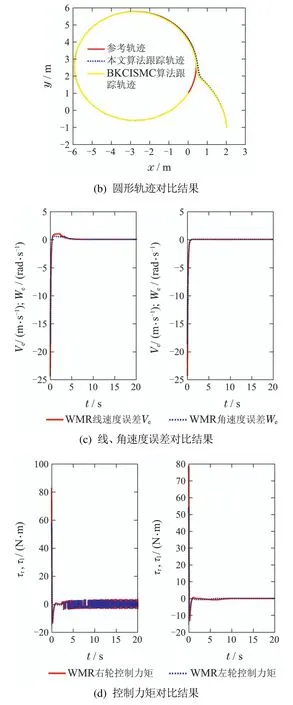
图5 轨迹跟踪对比Fig.5 Trajectory tracking comparison

文中算法比BKCISMC算法收敛速度更快图5(a)BKCISMC算法中,经5 s后位姿误差收敛到一个很小的区间内,并保持该区间内;而本文算法中,经3 s后位姿误差收敛到一个很小的区间内,并保持该区间内.图5(c)BKCISMC算法中,约4∼5 s后达到速度误差曲线拐点;而本文算法中,经1 s左右速度误差曲线拐点.

文中算法和BKCISMC算法都具有较好的鲁棒性,但是BKCISMC算法鲁棒性越强输入抖动越剧烈.当WMR受到滑动与打滑,WMR模型不确定性变化量和未知输入扰动的影响时,而它们的控制参数不变的情况下,从图5(a)–5(c)中可以看出位姿和速度跟踪误差收敛过程中仅发生了少许的变化.由图5(d)可知,本文算法的控制力矩输入不存在BKCISMC算法的控制力矩输入的抖动现象.

本文算法对滑动与打滑下集的总扰动d的估计值如图6.

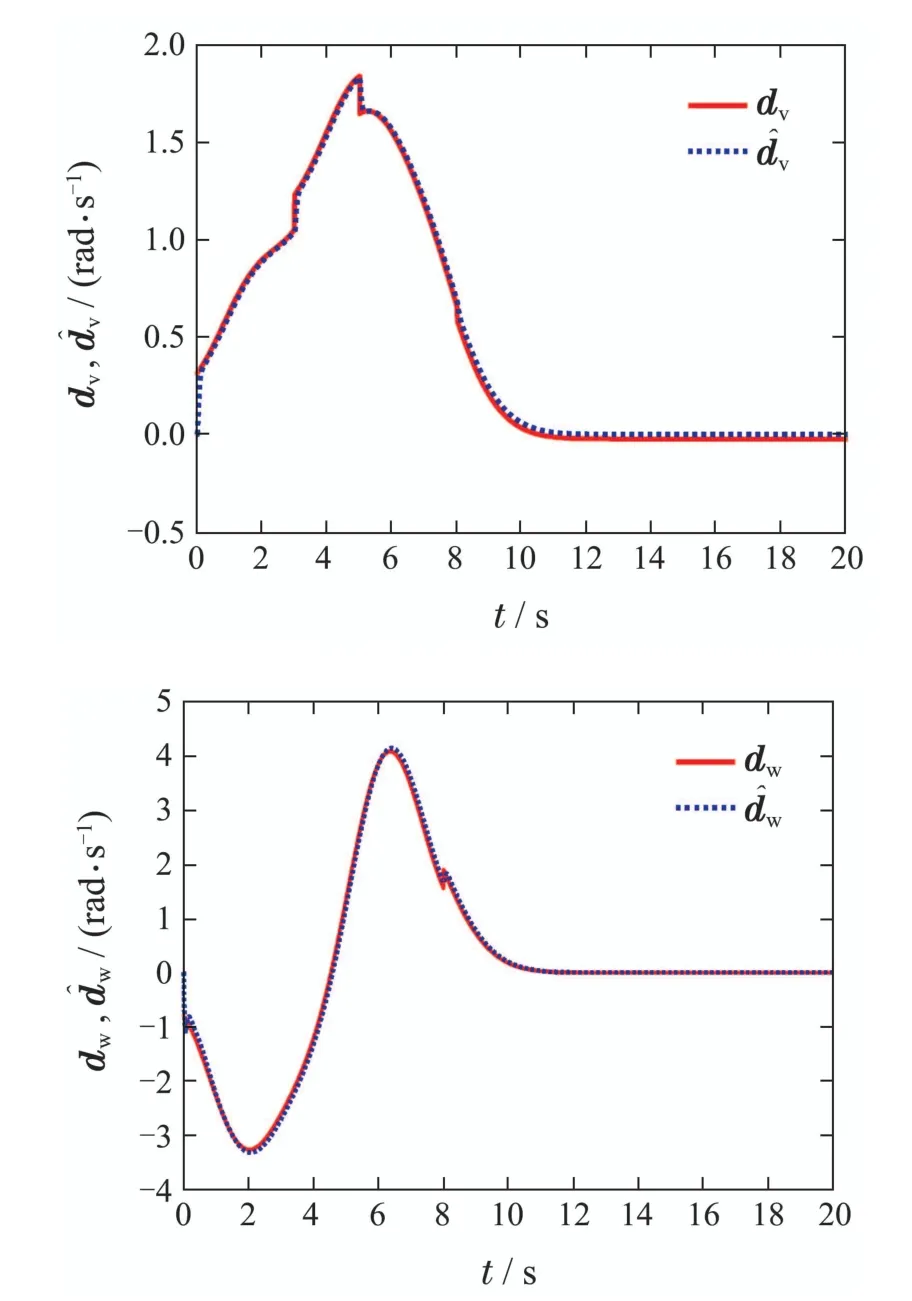
图6 滑动与打滑下集总扰动d的估计Fig.6 Estimation of lumped disturbance d under sliding and slipping

图6可以看出d估计值能十分接近其实际值,表明线性扩张观测器的收敛误差较小,对扰动的观测精度较高.

6 结论

针对滑动与打滑下的轮式移动机器人,本文基于自抗扰思想提出了含有集总扰动补偿的动力学控制器.由于滑动与打滑下的集总扰动是未知的,本文通过线性扩张观测器对集总扰动进行实时估计,并对动力学控制器进行前馈补偿,提高了控制器的精度和鲁棒性.最后仿真结果表明该控制器实现了轮式移动机器人在滑动与打滑条件下对参考轨迹的快速跟踪.即使轮式移动机器人在跟踪中存在着输入扰动和参数变化,本文的控制器仍具有良好的跟踪控制性能.

下一步的工作:搭建硬件实验平台,验证本文提出的控制器方案.考虑到机器人在实际实验情况下更为复杂,本文给出了自抗扰动力学控制器在实际应用中的两点建议:

1)通过减小线性扩张观测器的初始误差,可以提高轨迹跟踪的精度;

2)控制器带宽越大,动力学系统稳定性越好,不宜超出信号采样频率.根据实际情况,选择适当的控制器带宽,观测器带宽为控制器带宽3∼5倍.