一种基于无源性理论的模糊Hopfield神经网络学习律设计方法
2020-04-11婧柏建军薛安克
王 婧柏建军薛安克
(1.莱芜职业技术学院机械与汽车工程系,山东莱芜 271100;2.浙江省物联感知与信息融合技术重点实验室,浙江杭州 310018;3.杭州电子科技大学信息与控制研究所,浙江杭州 310018)
1 引言
模糊神经网络由于集合了神经网络与模糊系统的优点,得到了广泛的关注,并已成功应用到了非线性辨识、优化控制等领域[1–5].对于动态神经网络而言,系统的稳定性是网络能够正常工作的前提.然而,在实际中由于不可避免的会存在时间延迟现象,系统稳定性会变差,甚至会变得不稳定.因此,众多学者对具有时延的模糊神经网络系统的稳定性进行研究并取得了大量的成果[6–11].
另一方面,利用无源性理论,只需要研究系统的输入及输出特征即可进行系统的稳定性分析[12],因此,有许多研究者尝试利用无源性理论设计出使神经网络满足某些特性的权重矩阵的学习律.Yu等[9]对一类动态神经网络设计了基于无源性的学习律,并在此基础上对一类不同时间尺度的神经网络设计了无源的权重矩阵学习律[10].Ahn[11]将无源性理论引入到模糊Hopfield神经网络稳定性分析中,设计了一种保证系统输入到输出无源的权重矩阵学习律,并在该学习律基础上附加一定的条件可使系统满足输入到状态稳定.然而,文献[11]只对定常时滞情况进行了研究,对于时变时滞的情况目前还没有人研究.
本文针对具有时变时滞的模糊神经网络系统稳定性问题进行研究.首先,基于无源性理论,设计了一种权重矩阵学习律,并通过构造模糊Lyapunov函数,证明了该学习律可保证系统是无源的.然后,基于该学习律,证明了系统是从输入到状态稳定的.最后,通过一个仿真例子验证了本文方法的有效性.
2 问题描述
考虑如下模糊神经网络模型[13–14]:
规则i如果x1(t)是是那么
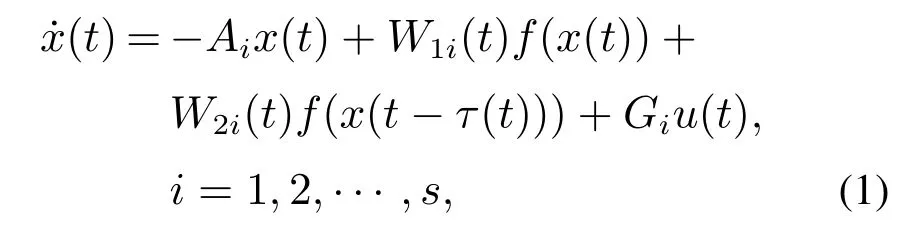
其中:i ∈表示第i条模糊规则;s ∈表示模糊规则个数;表示基于前提变量xj的论域;βij ∈{1,2,···,sj}标识前提变量xj属于论域上的第βij个模糊子集;sj是基于前提变量xj的论域上模糊子集个数;x(t)=[x1(t)x2(t)···xn(t)]T是神经元状态向量;u(t)=[u1(t)u2(t)···um(t)]T∈是 外部输入向量;τ(t)表示系统时变时滞,满足0τ(t)τM;ϕ(t)(−τMt0)表示系统状态初始值;Ai=diag{ai1,ai2,···,ain}(aij>0,j=1,2,···,n)是自反馈矩阵;W1i(t)表示神经网络内部联系权重矩阵;W2i(t)∈表示时滞联系权重矩阵;f(x(·))=[f1(x1(·))f2(x2(·))···fn(xn(·))]T∈表示神经元激励函数,通常是满足利普希茨条件的非线性函数;Gi ∈是已知常数矩阵,反映外部输入对神经元状态的影响程度.在不影响理解的前提下,本文用xt来代表x(t),ut来代表u(t).
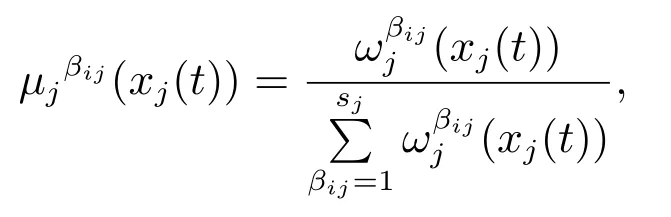
则规则i标准化后的隶属度函数为
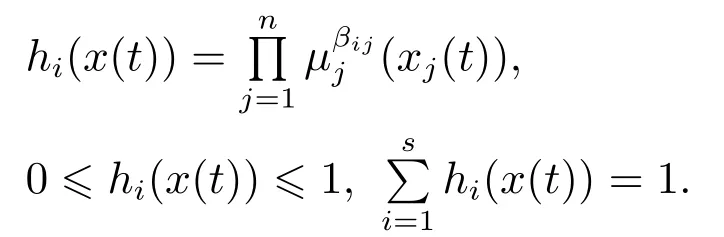
运用标准模糊推理方法进行处理,再进行去模糊化,得到的全局模糊神经网络模型可表示为
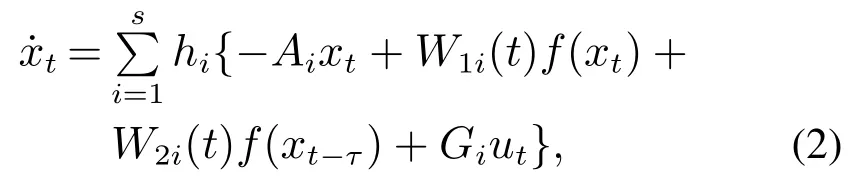
hi为hi(x(t))的简写,τ为τ(t)的简写.
以下为本文中比较重要的几个定义和引理.考虑如下的系统:
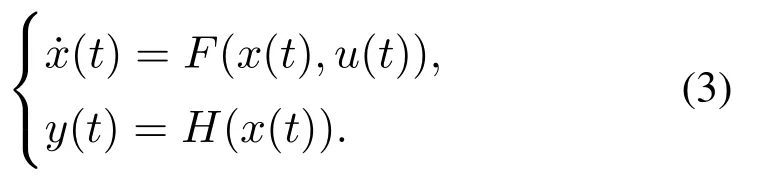
定义1[12]如果存在一个非负常数δ和半正定函数Ω(·)0满足
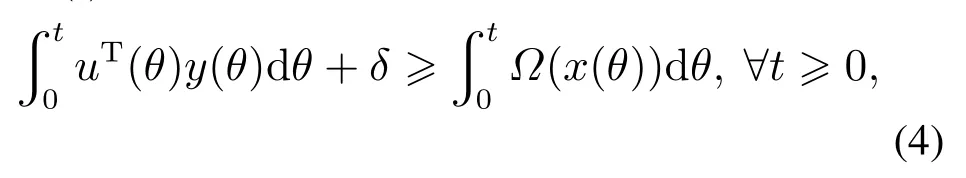
则称系统从输入u(t)到输出y(t)是无源的.
引理1[15]连续函数V(·):对于任意x(t)∈如果存在K∞函数α和β使得
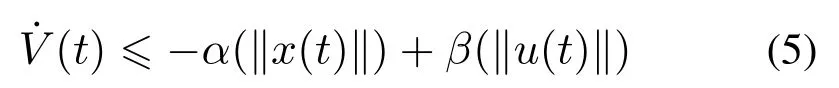
成立,则称系统是输入到状态稳定的.
引理2[11]给定适当维数矩阵或向量U和V,对于任意正实数α,不等式
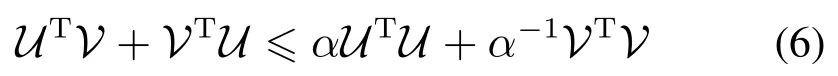
总是成立的.
3 主要结论
本节基于模糊Lyapunov函数,对如式(1)所描述的T–S模糊时滞神经网络系统设计了系统输入到输出无源的权重矩阵学习律,并证明了在该学习律下,系统是输入到状态稳定的.
定理1给定对称矩阵S >0,如果存在式(12)所定义的对称矩阵Pi >0(i=1,2,···,s)使得线性矩阵不等式(7)和(9)成立,且权重矩阵W1i(t),W2i(t)(i=1,2,···,s)分别遵循式(9)和式(10)的学习律,则系统(2)是从外部输入到输出无源的.输出y(t)∈如式(11)所示.

证考虑如下Lyapunov函数:
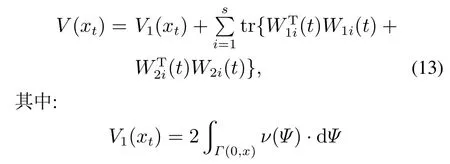
是沿路径Γ(0,x)的积分函数,ν(xt)=对V(xt)沿着系统(2)的状态运动轨迹对时间t求导得
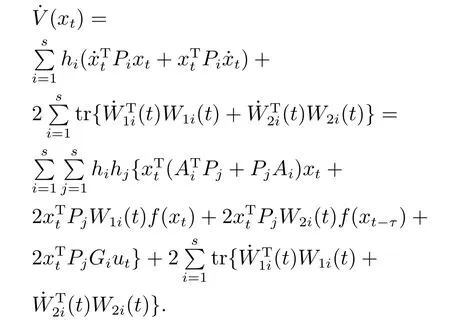

如果权重矩阵W1i(t)和W2i(t)分别满足式(9)和式(10),则有
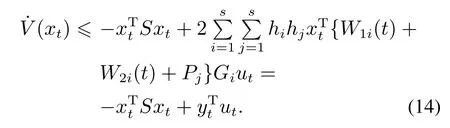
对上式两端从0到t作积分,可以得到
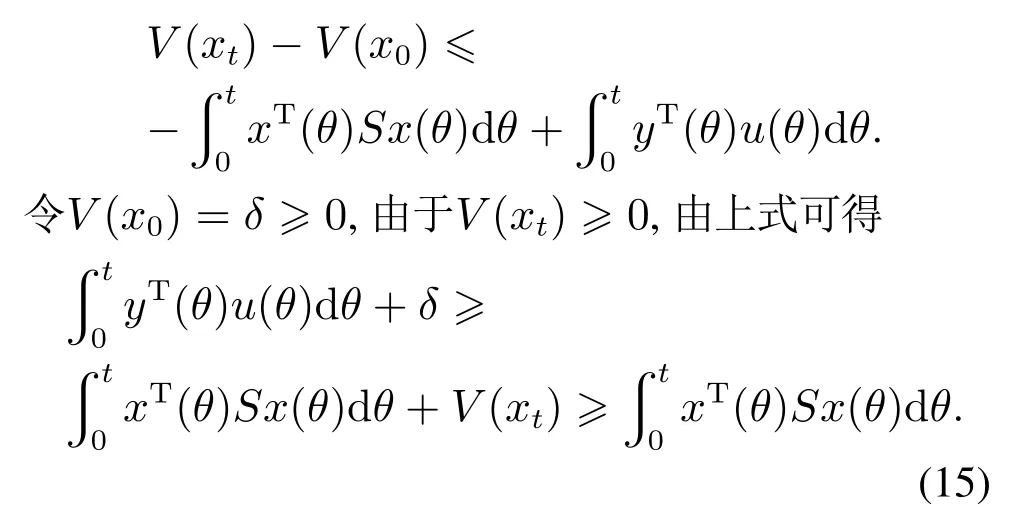
根据定义1可得,系统从外部输入到输出是无源的.定理1得证. 证毕.
以下定理证明了在上述学习律的条件下,系统是输入到状态稳定的.
定理2在条件(7)和(9)满足的前提下,权重矩阵学习律(9)和(10)使得系统(2)是从输入到状态稳定的.
证根据引理2可知
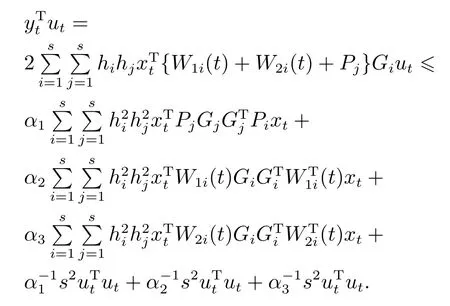
由式(14)可得
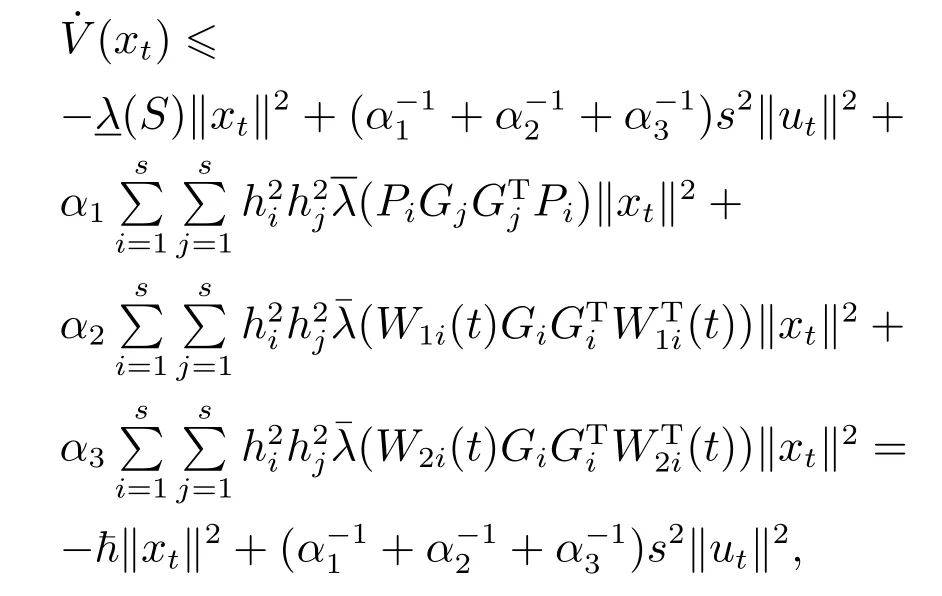
其中
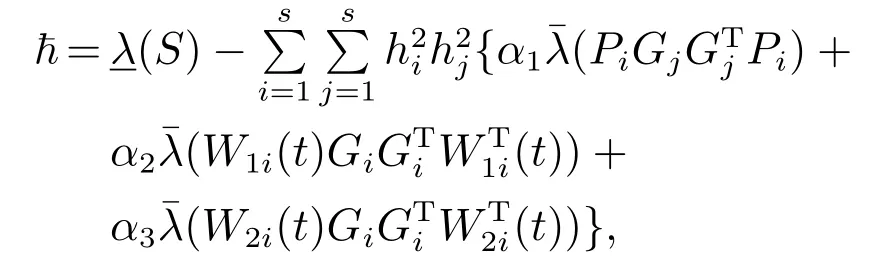
其中:α1,α2,α3为任意大于0的正数,表示最大特征值,表示最小特征值.不难看出,如果S存在,总能够找到任意的α1,α2,α3使得>0.根据引理1,系统(2)是从输入到状态稳定的.
定理2得证. 证毕.
4 仿真实例
在这节中,将通过数值仿真来验证本文所提方法的有效性.
例1考虑以下模糊系统:
规则1 如果x1(t)是接近“0”的,那么
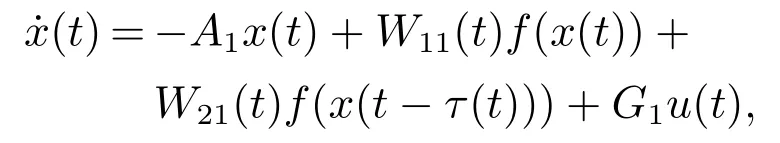
规则2 如果x1(t)是接近“1”或“−1”的,那么
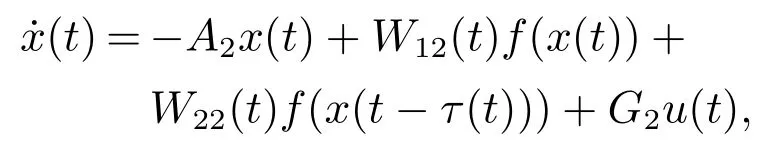
其中相应参数为
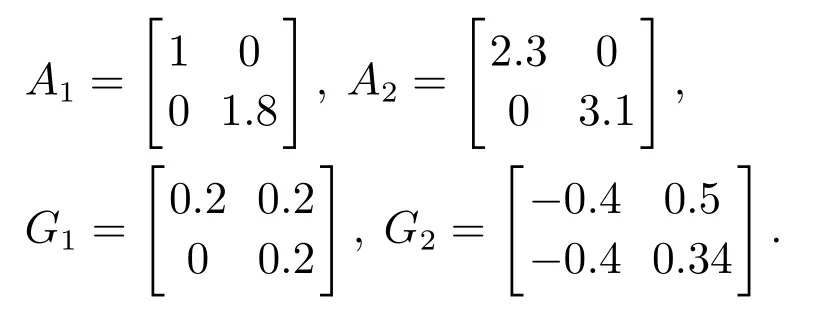
隶属度函数定义如下:

W21(t),W12(t),W22(t)有类似定义,τ(t)=0.4+0.4 cost,则τM=0.8,u(t)=[0.2 sint0.2 cost]T,ϕ(t)≡[0.5−0.4]T(−τMt0),各个权重矩阵在t=0时刻的初始值为
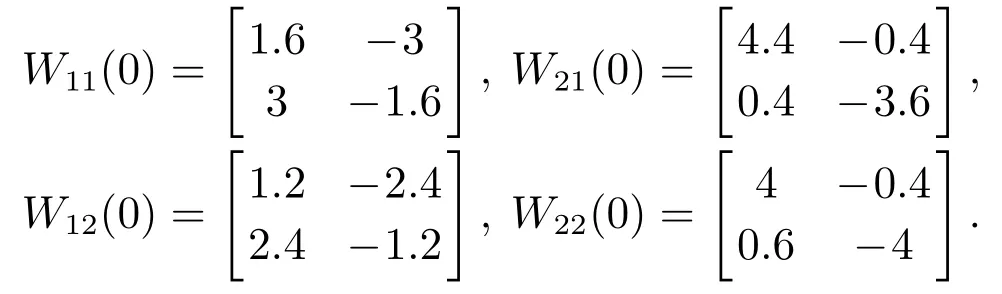
本文在仿真时发现,当Pi(i=1,···,s)较大时,系统轨迹震荡较大.为了避免系统剧烈的震荡,在求解LMIs(7)–(9)时加入以下条件以求得尽可能小的Pi值.
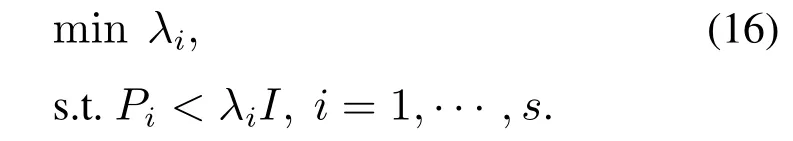
取S=运用MATLAB中LMI工具箱对式(7)–(9)及式(16)求解,可得
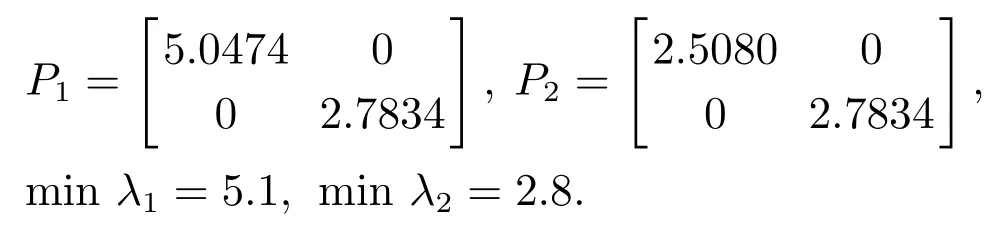
系统状态轨迹图如图1所示.权重矩阵随时间变化如图2–5所示.由图可知,运用本文所提的方法,系统是输入到状态稳定的.

图1 系统状态轨迹图Fig.1 System state trajectories
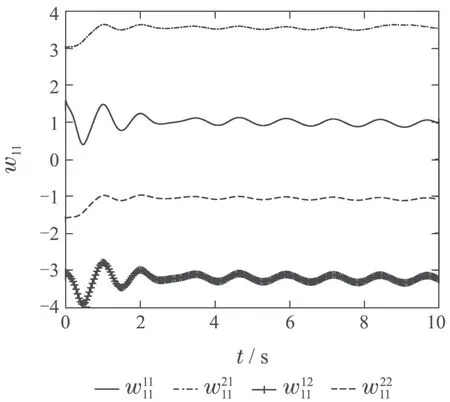
图2 W11(t)更新过程Fig.2 W11(t)update process
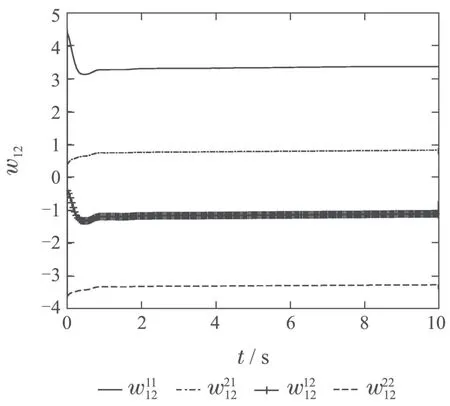
图3 W12(t)更新过程Fig.3 W12(t)update process
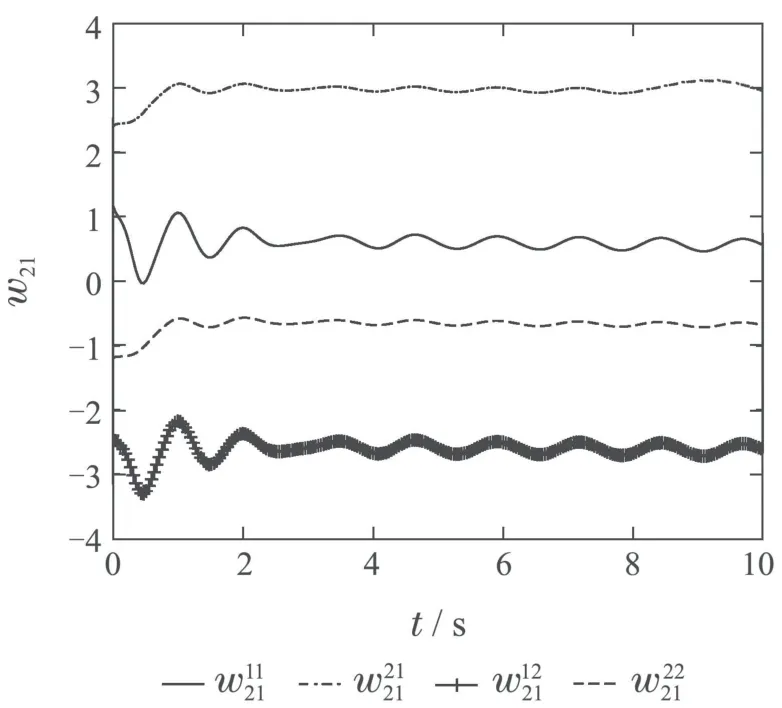
图4 W21(t)更新过程Fig.4 W21(t)update process
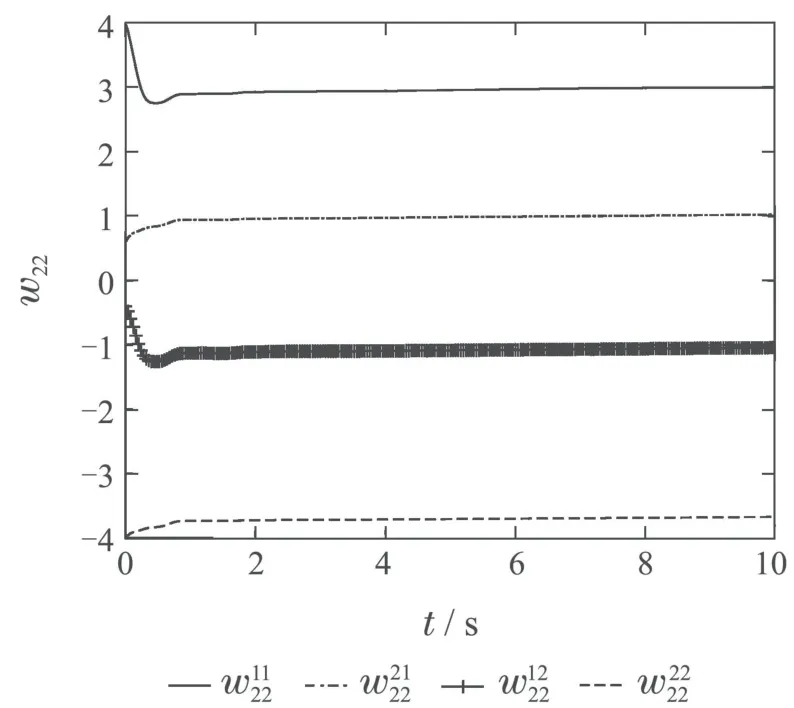
图5 W22(t)更新过程Fig.5 W22(t)update process
文献[11]基于公共Lypunov 的方法设计了模糊Hopfield神经网络的一种权值学习律.令本文中的P1=P2=···=Ps=P,则本文中的结论将退化为文[11]中的结论.利用LMI工具箱可得如下解:

系统状态轨迹图的对比如图6–7所示,不难看出,采用本文给出的学习律,系统的状态震荡比文[11]要小一些.
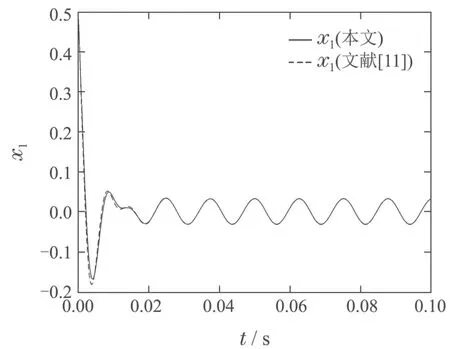
图6 x1对比图Fig.6 x1comparison
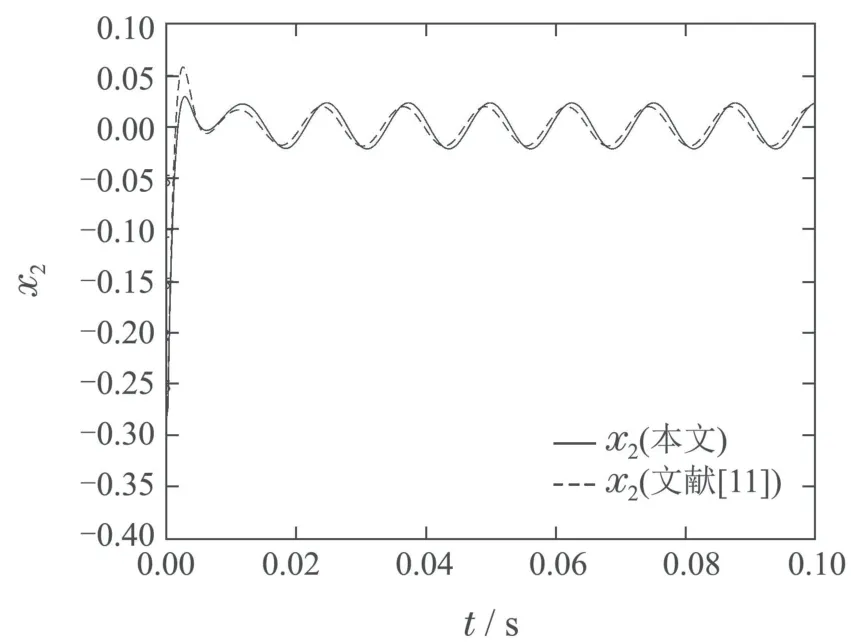
图7 x2对比图Fig.7 x2comparison
5 结论
本文对一类带有时变时滞的模糊神经网络系统的稳定性问题进行研究,基于无源性理论,给出了一种新的权重矩阵学习律,通过构造模糊Lyapunov函数证明了系统是输入到输出无源的,并在此基础上证明了系统是输入到状态稳定的.最后,通过数值仿真,验证了本文所提方法的有效性.
