面向不完备混合数据的矩阵增量知识维护方法研究

黄倩倩，李天瑞，杨 新，王国强，胡 节

1(西南交通大学 计算机科学与技术学院，成都 611756)2(西南交通大学 人工智能研究院，成都 611756)

1 引 言

1982年，波兰学者Pawlak在经典集合论的基础之上提出了粗糙集理论(Rough Set theory)[1，2].此后，该理论逐渐成为一种定量分析处理不精确、不一致和不完整信息与知识的有效数学工具.相较于模糊集和概率论等其他不确定性理论，粗糙集最大的优势在于其不需要任何邻域的先验知识，就能有效地刻画和分析不确定性问题.近30年来，粗糙集理论和方法已被广泛应用于机器学习与知识发现、数据挖掘、模式识别和图像处理等多个领域[3-7].

经典粗糙集模型通过一个等价关系(满足自反性、对称性和传递性)仅适用于处理名义型数据.这大大限制了粗糙集的适用范围.大数据环境下信息的全面感知，使得所获得的数据不再局限于某个单一的数据类型，其中名义型和数值型类型共存于的混合数据是最为普遍的现象.为了运用粗糙集理论处理混合数据，众多学者开展了一系列的工作研究粗糙集的各种拓展模型.针对数值型数据，最为常见的做法就是将数值型数据进行离散化处理[8，9]，这就使得某些重要信息在转化过程中丢失.因此，Lin等通过介绍了邻域系统的概念，提出了邻域粗糙集模型[10].Li等提出了基于邻域的决策粗糙集模型用来处理包含噪声的数值型数据[11].随后，Hu等通过引入异构欧式重叠距离函数来刻画同时具有名义属性和数值属性的对象之间的关系，提出了一种基于δ-邻域关系的邻域粗糙集模型[12].Chen等将偏序关系引入具有名义型属性和数值型属性的混合有序决策系统中，介绍了优势邻域粗糙集模型，并给出了面向混合数据的并行属性约简算法[13].近些年来，邻域粗糙集模型已经吸引了众多学者的注意并被广泛应用于多个领域[14-17].

考虑到现实环境中数据采集过程中设备故障、存储介质损坏、传输媒体堵塞和人为遗漏等因素，使得所收集的数据常常包含缺失值，即信息系统是不完备的.因此，如何高效地利用粗糙集理论和方法处理具有缺失值的信息系统已然成为当前知识发现领域中的一个研究热点[18-25].在对于具有缺失名义型数据和数值型数据的混合信息系统的研究过程中，Jing等通过定义了新的距离函数，并结合概率的方法，提出了一种基于容差关系的变精度容差邻域粗糙集模型[26]；Zhao等基于邻域容差关系提出了一种扩展的粗糙集模型，并介绍了混合特征选择方法[27]；与此同时，姚晟等提出了一种拓的不完备邻域粗糙集模型，并构造了一种基于邻域混合熵的不完备邻域粗糙集属性约简算法[28]；黄恒秋等通过引入一种新的不确定距离度量函数，提出了基于联系度距离函数的双邻域粗糙集模型[29].此外，钱文彬等基于一种新的完备邻域容差关系，通过改进不可区分类的损失函数区间值的获取方法，构建面向不完备混合信息系统的三支决策模型[30].

基于以上的研究工作，我们发现现今的不完备混合信息系统中缺失值的含义仅仅局限于某一种语义解释，并不适合处理“不关心值”和“丢失值”共存的不完备混合信息系统.因此，本文将定义两种新的邻域关系，即邻域特征关系和量化邻域特征关系，并基于这两种关系构建拓展的邻域粗糙集模型，从而有效地处理不完备混合信息系统.此外，利用相关的矩阵和运算，介绍粗糙邻域近似知识的矩阵计算方法.最后，当不完备混合信息系统中属性随着时间发生变化时，提出基于矩阵的增量知识维护机理和方法，这对丰富动态知识更新和知识获取理论有着重要的意义.

2 相关知识

2.1 不完备信息系统

传统粗糙集理论中，设四元组S=(U,A,V,f)是一个信息系统，其中，U={u1，u2，…，un}和A={a1，a2，…，al}分别表示非空有限的对象集合和属性集合;V=∪a∈AVa为所有属性值的集合，Va表示属性a的值域;f:U×A→V为一个信息函数，即:对于任意u∈U和a∈A有f(u，a)∈Va.特别地，若A=C∪D，其中C和D分别为条件属性集和决策属性集，那么信息系统称之为决策表.

定义1[1].给定一个信息系统S，对于任意子集Q⊆C，论域上关于Q的不可区分关系定义为：

RQ={(u，v)∈U2|∀a∈Q，f(u，a)=f(v，a)}

(1)

显然，不可区分关系RQ满足自反性，对称性和传递性，因此是一个等价关系.若存在a∈C和u∈U使得f(u，a)=*或f(u，a)=?，那么信息系统S被称为不完备信息系统，其中“*” 和 “?” 分别表示 “不关心值” 和 “丢失值”.等价关系因其自身的局限性，并不能有效的处理不完备信息系统.因此，Grzymala-Busse提出了特征关系[23]，其可被视为容差关系[18]和相似关系[20]的一种泛化表现形式.

定义2[23].设S为不完备信息系统，对于任意子集Q⊆C，论域上关于Q的特征关系定义为：

KQ={(u，v)∈U2|∀a∈Q，f(u，a)=?∨(f(u，a)=

f(v，a)∨f(u，a)=*∨f(v，a)=*)}

(2)

由上述定义可知，特征关系KQ仅仅满足自反性，不一定满足对称性和传递性.对于任意一个对象u∈U，令KQ(u)表示u基于特征关系KQ的特征类，即KQ(u)={v∈U|(u，v)∈KQ}.

定义3[23].设S为不完备信息系统，∀X⊆U，Q⊆C.则X基于特征关系KQ的上、下近似集分别定义为：

(3)

2.2 邻域粗糙集

通过从拓扑空间中引入邻域概念，Hu等提出了一个邻域关系处理名义属性和数值属性共存的混合信息系统[12].给定一个信息系统S和一个阈值δ，∀Q⊆C.对于任意一个对象u∈U，δQ(u)表示u关于Q的邻域，即：

δQ(u)={v∈U|ΔQ(u，v)≤δ}

(4)

其中，Δ是一个距离函数(满足正则性，对称性和三角不等性).目前，Minkowski距离，作为一个重要的度量函数，已被广泛应用于机器学习和模式识别领域，其定义如下：

(5)

当p=1时，称为Manhattan距离；当p=2时，称为Euclidean距离；当p=时，称为Chebychev距离.

定义4[12].设S为一个信息系统，对任意子集Q=QC∪QS⊆C，其中QC和QS分别是名义型属性集和数值型属性集，论域上关于Q的邻域关系定义为：

NQ={(u，v)∈U2|ΔQC(u，v)=0∧ΔQS(u，v)≤δ}

(6)

显然，邻域关系仅满足自反性和对称性，不一定满足传递性.因此，对于任意对象子集X⊆U，X基于邻域关系NQ的上、下近似集定义为：

(7)

2.3 不完备混合信息系统

定义5.设S=(U，A，V，f)是不完备混合信息系统，其中：

1)U={u1，u2，…，un}是非空有限的对象集合，称为论域；

2)A=AC∪AS(AC∩AS=∅)是非空有限的属性集合，AC和AS分别为名义型属性集和数值型属性集；

3)V=∪a∈AVa，Va表示属性a的值域；

4)f：U×A→V为一个信息函数，使得∀a∈A，u∈U有f(u，a)∈Va；

5)存在某个属性a∈A，使得f(u，a)=*或f(u，a)=?.

表1 一个不完备混合决策系统
Table 1 An incomplete hybrid decision system

Ua1a2a3a4du1210.52.0Nu2110.71.8Yu3∗00.51.5Yu41?0.92.1Nu510?1.9Yu62∗0.2∗N

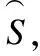
3 不完备混合信息系统中邻域粗糙集模型

接下来，将介绍两种新的邻域关系(邻域特征关系和量化邻域容忍关系)来处理本文所提出的不完备混合信息系统.

3.1 邻域特征关系

定义6.设S是一个不完备混合信息系统，对任意属性子集Q=QC∪QS⊆A，论域上关于Q的邻域特征关系的定义为：

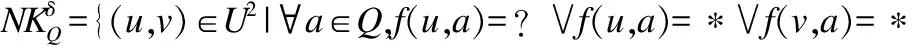
(8)

其中，δ为一个给定的阈值.

(9)

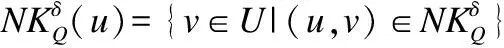
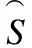
(10)

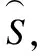
证明：

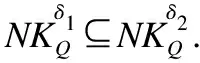
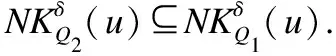
同理可证其余情况.

粗糙集理论中，近似分类精度是一个非常重要的评价指标，用于描述近似分类的不确定性度量.

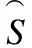
(11)

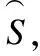
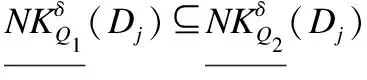
同理可证其余情况.

3.2 量化邻域特征关系

受到数据驱动数据挖掘思想的启发，Wang等提出数据驱动量化容忍关系处理由名义型数据组成的不完备信息系统[31].显然，这种关系并不适合用来处理本文介绍的不完备混合信息系统.因此，基于数据驱动的思想，针对名义型数据和数值型数据，我们引入两个新的度量函数，从而提出一个新的邻域关系.

定义10.设S是一个不完备混合信息系统，A=AC∪AS.令ρC：U2×AC→和ρS：U2×AS→分别是关于AC和AS的两个度量函数，具体定义如下：

(12)

和：

(13)

其中，λ1和λ1是阈值，且0≤λ1，λ2≤1.

表2 相关符号说明
Table 2 Description of related symbols

符号含 义a∈AC一个名义型属性b∈AS一个数值型属性Via(1≤i≤m1)关于属性a的第i个已知属性值Vjb(1≤j≤m2)关于属性b的第j个已知属性值Ha属性a下所有属性值为已知值的对象集合Hb属性b下所有属性值为已知值的对象集合sia集合{u∈U|f(u,a)=Via}的基数njb集合{u∈U|u∈Hb→|f(u,b)-Vjb|≤δ}的基数

定义10中所涉及的相关符号的具体含义可见表2.注意，∀a∈AC，∀b∈AS，函数ρC和ρS具有如下性质：

1.满足正则性；

2.不一定满足对称性，如ρC(u1，u4，a2)≠ρC(u4，u1，a2)；

3.不一定满足三角不等性，如令λ1=0.5，有ρC(u1，u6，a2)=ρC(u6，u4，a2)=0和ρC(u1，u4，a2)=，则ρC(u1，u4，a2)>ρC(u1，u6，a2)+ρC(u6，u4，a2).

因此，ρC和ρS被称为伪度量函数.

定义11.设S是一个不完备混合信息系统，对任意属性子集Q=QC∪QS⊆A，论域上关于Q的量化邻域特征关系的定义为:

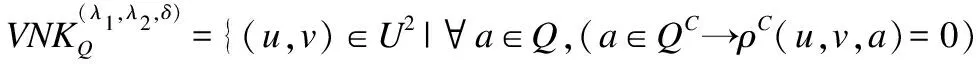
(14)

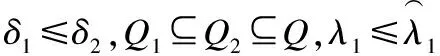
证明：证明过程与性质1的证明相似，故省略.

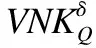
(15)

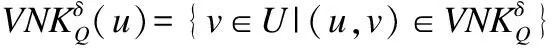
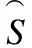
(16)

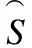
(17)

3.2 邻域特征关系和量化邻域特征关系之间的关系

基于上述两种新的邻域关系的定义，我们可以得到以下定理.

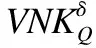
证明：

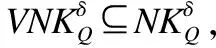
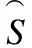
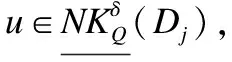
例2.表1给出了一个不完备混合决策系统，令δ=0.3和λ1=λ2=0.5.首先，基于决策属性D，可得U/D={D1，D2}，D1={u1，u4，u6}和D2={u2，u3，u5}.其次，根据定义6有:

则可得关于D1和D2的一对近似集：

由定义8可得:

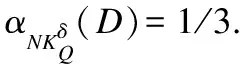
4 不完备混合信息系统中基于矩阵的近似集计算方法

通过引入决策矩阵、关系矩阵和相关的诱导矩阵，我们将介绍不完备混合信息系统中计算近似集的矩阵方法.

定义15.设U={u1，u2，…，un}为所有对象形成的集合，∀X⊆U，则称为X的特征向量，其中:

(18)

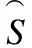
(19)

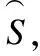
1)DM=[G(D1)，G(D2)，…，G(Dm)]；

证明：根据定义15和定义16，易知结论成立，故此省略证明过程.

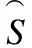
(20)

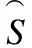
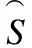
ΩQ=ΛQ·(MQ·DM)

(21)

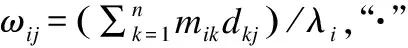
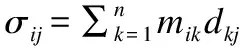
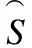
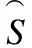
(22)

⟹φi>0

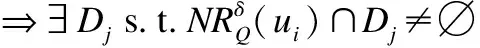
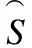
(23)

基于以上对不完备混合信息系统中基于矩阵运算的近似集构造方法的讨论和分析，我们设计了一种计算近似集的静态算法，即算法1.

算法1.不完备混合信息决策系统中基于矩阵的近似集静态计算算法.

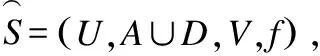
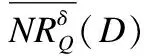
Step 1.fori= 1 ton/*构造决策矩阵DM的元素*/

forj=1 tom

if (ui∈Dj) then

dij=1；

else

dij=0；

end for

end for

Step 2.fori= 1 ton/*构建矩阵MQ和ΛQ*/

λi=0；

forj=1 ton

mij=1；

λi=λi+mij；

else

mij=0；

end for

end for

Step 3.fori= 1 ton

φi=0；

forj=1 tomdo

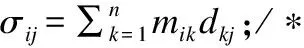
ωij=σij/λi；/*计算中间矩阵ΩQ*/

φi=max(φi，ωij)；/*计算基本向量ΦQ*/

end for

end for

ori= 1 ton

if (φi>0) then

if(φi==1)then

end for

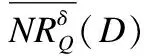
例3.由表1所示，可知D1={u1，u4，u6}，D2={u2，u3，u5}，根据定义16有：

基于定义18，有：

因此，根据推论2可计算D1和D2的上、下近似集为：

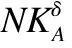
根据定理2，可知:

5 属性集变化时不完备混合信息系统中基于矩阵的近似集增量更新方法

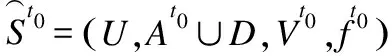
5.1 属性集增加的情形

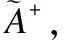
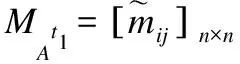
(24)

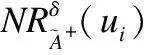
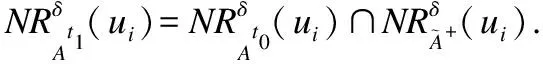
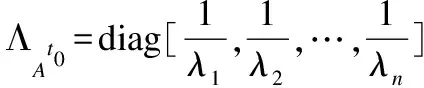
(25)

其中，“⊕”表示异或运算.

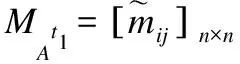
(26)

根据上述已给出的相关理论分析，我们设计了增加属性集时基于矩阵的近似集增量更新算法，即算法2.

算法2.不完备混合决策系统中属性动态增加时基于矩阵的近似集增量更新算法.

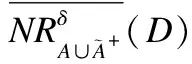
forj= 1 ton

if (mij==1) then

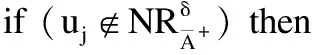
mij=0；

λi=λi-1；

fork=1 tom

σik=σik-dik；

end for

else

mij=1；

end for

end for

Step 2.fori= 1 ton

φi=0；

forj= 1 tomdo

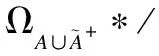
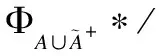
end for

end for

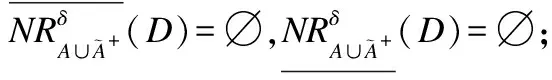
fori= 1 ton

if(φi>0) then

if(φi==1) then

end for

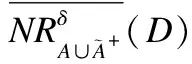
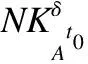
根据推论2，计算D1和D2的近似集为:

表3 属性增加时不完备混合决策系统
Table 3 Incomplete hybrid decision system
with adding attribute

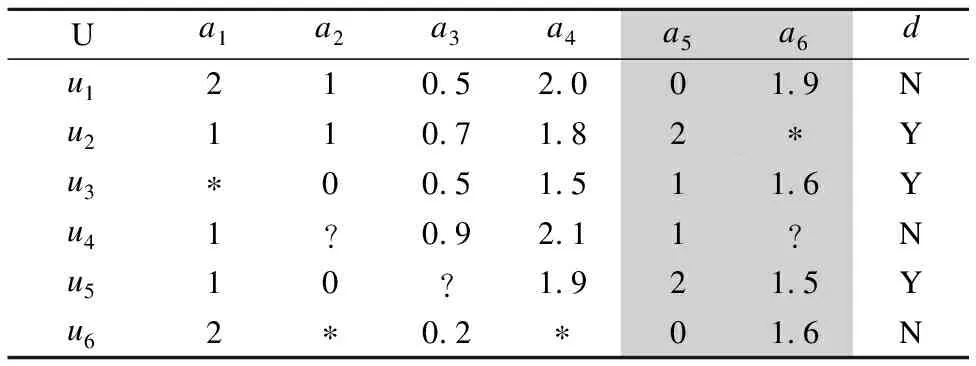
Ua1a2a3a4a5a6du1210.52.001.9Nu2110.71.82∗Yu3∗00.51.511.6Yu41?0.92.11?Nu510?1.921.5Yu62∗0.2∗01.6N

5.2 属性集删除的情形

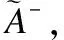
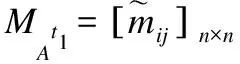
(27)

证明：证明过程与定理3的证明过程类似，故略.

(28)

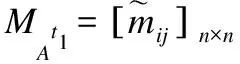
(29)

根据上述已给出的相关理论分析，我们设计了删除属性集时基于矩阵的近似集增量更新算法，即算法3.

算法3.不完备混合决策系统中属性动态删除时基于矩阵的近似集增量更新算法.

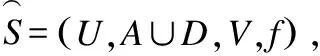
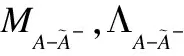
forj= 1 ton

if (mij==0) then

mij=1；

λi=λi+1；

fork=1 tom

σik=σik+dik；

end for

else

mij=0；

end for

end for

Step 2.fori= 1 ton

φi=0；

forj= 1 tomdo

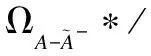
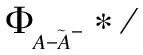
end for

end for

fori= 1 ton

if (φi>0) then

if (φi==1) then

end for

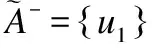
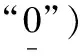
基于推论7，由关系矩阵诱导的对角矩阵被更新为：

再结合推论8和推论9，中间矩阵被更新为：

由推论2，可计算D1和D2的上、下近似集：

表4 属性删除时不完备混合决策系统
Table 4 Incomplete hybrid decision system
with deleting attributes

Ua2a3a4du110.52.0Nu210.71.8Yu300.51.5Yu4?0.92.1Nu50?1.9Yu6∗0.2∗N

6 结 论

本文以具有缺失名义型数据和数值型数据的不完备混合信息系统为研究对象，通过整合邻域关系和特征关系的特点，提出了邻域特征关系.与此同时，通过引入数据驱动数据挖掘的思想，进一步推广了邻域特征关系，定义了量化邻域特征关系.基于这两种关系介绍了两种拓展邻域粗糙集模型，并研究了其相关性质，丰富了邻域粗糙集理论框架.此外，通过引入决策矩阵、关系矩阵等相关矩阵，介绍了基于矩阵的粗糙邻域近似知识的计算方法.

随着信息技术的快速发展，实际环境中所收集的数据总是呈现出动态性变化，如何利用已有的结果高效、及时地获取知识已然成为亟待解决的问题.因此，针对不完备混合信息系统中属性集的增加和删除，提出了基于矩阵的增量知识维护机制，并通过具体的实例展现了所提出方法的有效性.在未来的工作中，利用UCI数据集测试增量更新方法的性能，以及通过运用云计算等并行技术来提高不完备混合信息系统中动态知识获取方法的效率将是我们研究的重点.