一种面向混合属性数据的邻域粒离群点检测

李 毅，胡建成

(成都信息工程大学 应用数学学院，成都 610225)

1 引 言

离群点检测是数据挖掘的重要研究方向之一，其目的是找出数据集中行为与其他对象很不相同的对象[1].离群点检测有很多应用，如入侵检测、信用卡诈骗和医学诊断等[2].因此，对离群点检测的研究是非常有必要的.

近几十年来，离群点检测的研究非常普遍，提出了许多离群点检测方法.现有的离群点检测方法主要包括极值分析、概率统计模型、线性模型、基于邻近性的模型、信息理论模型和高维离群点检测[2].其中，基于邻近性的模型主要包括三种方法：1)基于聚类的方法[3]；2)基于距离的方法[4，5]；3)基于密度的方法[6].然而，大多数基于距离的算法都是利用欧氏距离来设计的.在实际应用中，欧氏距离可能不是检测分类和混合属性数据离群值的最佳方法.

粗糙集理论(Rough Set Theory，RST)是由Pawlak在1982年提出的[7]，并得到了许多学者地不断改进.它为不充分和不完备分类属性数据的特征选择、分类规则学习和离群点检测等提供了形式化的框架.如前所述，大多数基于距离的方法都使用欧氏距离来计算两个数据对象之间的距离.然而，分类属性值之间并没有固有的距离度量，因此不能有效地处理包含分类属性的数据.此外，经过分析发现大多数离群点检测方法基本上都是用确定性的方式来表示和处理数据，没有考虑数据集的不确定性和不完备性.然而，现实生活中采集的数据集中存在大量的不确定性和不完备性数据.基于这些原因，提出了多种基于粗糙集的检测方法[8-12].例如，Chen等人以粗糙集为基本框架提出了一种基于粒计算(Granular Computing，GrC)的检测方法[8].该方法基于等价关系和等价类建立数学模型，其检测模型只适用于分类属性而不是数值属性数据集.这些检测模型在处理数值属性数据时，需要离散化处理，从而提高数据处理所用时间，并伴随着明显的信息丢失，因此影响检测的准确性.此外，为处理数值和混合属性数据，Hu等人提出了一种邻域粗糙集模型，并在此基础上提出了特征选择算法[13].邻域粗糙集是一种强大的数据挖掘工具，用于数值和混合属性特征选择、分类和不确定性推理等[13，14].然而，近年来邻域粗糙集模型中混合属性离群点检测的报道较少[15-18].

基于这些讨论，本文在邻域粗糙集的基础上，构造了一种基于邻域粒的混合属性离群点检测方法.首先，该方法优选混合邻域距离度量和统计值的邻域半径以构建邻域信息系统.其次，定义粒离群程度和离群因子来分别表征邻域粒和对象的离群性，并设计了相关的基于邻域粒的离群点检测(Neighborhood Granule-based Outlier Detection，NGOD)算法.对比实验结果表明，该方法比现有的离群检测方法具有更好的适应性和有效性.它可以应用于三种数据，包括分类、数值和混合属性数据.

2 预备知识

在本节中，将介绍邻域粗糙集[13]中的一些基本概念.

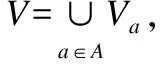
定义 1[13].给定任意的xi∈U和B⊆C，特征空间B中xi的邻域δB(xi)定义为：

δB(xi)={xj|xj∈U,ΔB(xi,xj)≤ε}

(1)

其中，ε是邻域半径，ΔB(xi,xj)是一个关联于B的距离函数.对∀xi,xj,xk∈U,ΔB(xi,xj)满足：

1)ΔB(xi，xj)≥0⟺xi=xj，ΔB(xi，xj)=0；

2)ΔB(xi，xj)=ΔB(xj，xi)；

3)ΔB(xi，xk)≤ΔB(xi，xj)+ΔB(xj，xk).

模式识别中有多种距离函数.如闵可夫斯基距离(包括曼哈顿距离、欧式距离和切比雪夫距离)、混合欧式重叠度量和值差异度量等[19].例如，关于C的混合欧式重叠度量(Heterogeneous Euclidean Overlap Metric，HEOM)函数定义为：

(2)

其中：

其中ωcj是属性cj的权重，maxcj和mincj分别表示属性cj的最大值和最小值.

δB(xi)是以对象xi为中心的邻域粒，邻域大小取决于阈值ε，如果ε取较大值，则更多的对象落在xi的邻域内.

通过以上讨论，可以看到影响邻域的主要因素有两个：一个是所使用距离函数，另一个是阈值ε.第一个决定了邻域的形状，而阈值ε控制着邻域粒的大小.此外，还可以看到，如果让ε=0，邻域粒退化为等价类.在这种情况下，相同邻域粒中的样本是等价的，邻域粗糙集模型退化为Pawlak粗糙集.因此，邻域粗糙集是Pawlak粗糙集的自然推广.

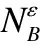
显然，邻域关系是一类相似关系，它满足自反和对称的性质.邻域关系将对象汇集到一起，以距离表示相似性或不可分辨性，同一邻域粒内的样本彼此接近.

邻域粒族{δB(xi)|xi∈U}形成了一个基本粒系，它覆盖了论域，而不是将论域划分开来.我们有：

1)∀xi∈U;δ(xi)∉∅;

3 基于邻域粒的混合属性离群点检测

在本节中，首先建立了相关的检测系统，其次构建了离群点检测模型，最后设计了相应的检测算法.

3.1 检测系统

在本小节中，构建了一个用于离群点检测的邻域信息系统，主要包括归一化预处理、邻域距离度量的选取和邻域半径的标准设置.

邻域粗糙集中的数据处理通常存在大小和维数的差异.为了获得准确的数据处理结果，在数据处理前对原始的数值属性数据进行归一化处理.本文具体采用以下公式形式的最小-最大归一化方法：

(3)

显然，归一化后，这些数值属性的属性值范围为[0，1].

为了有效地处理数值和混合属性数据集，本文重新定义HEOM度量如下.

定义 2.对任意x，y∈U，x与y关联于B的混合欧式重叠度量定义为：

(4)

其中：

现实生活中的大多数数据都是混合的.从以上定义可以看出，HEOM不仅可以处理数值数据，还可以同时处理数值和分类属性组合的混合数据.因此，本文采用HEOM度量作为邻域距离度量.

数据对象的邻域获取涉及到邻域半径，邻域半径通常由专家根据经验确定[13，15].例如，如果采用文献[15]中邻域半径的设置方法，所涉及的参数将与属性数m相同.显然，它是主观的和随机的，这导致了算法对参数选择的敏感性.此外，降低算法对专家指定参数的敏感性是提高算法精度的客观依据.因此，对象x相对于属性cj的邻域半径设为[16]：

(5)

1https：//github.com/BElloney/Outlier-detection

其中std(cj)表示数值属性值的标准差，λ是半径调整的给定参数.

3.2 检测模型

为了计算粒之间的距离，文献[8]定义了重叠距离度量.同理，为了能有效处理数值和混合属性数据，在邻域粗糙集的邻域重叠度量(Neighborhood Overlap Metric，NOM)定义如下.

定义 3.给定一个信息系统IS.对x，y∈U，对象x与y之间的邻域重叠度量定义为：

NOM(x，y)=|{cj∈C|y∉δ{cj}(x)}|

(6)

定义 4.对ngi，ngj∈NGB，邻域粒ngi与ngj的距离定义为：

(7)

对于任何对象xi∈U，大多数当前离群点检测方法仅给出xi的二进制分类，即xi是或不是离群点[6].但是，在许多情况下，为xi指定一个离群因子更有意义.在下文中，定义了两个概念：“粒离群度(GOD)”和“基于邻域粒的离群因子(NGOF)”，其中前者量化给定邻域粒的离群特性，后者表示给定的对象离群特性.

定义 5.对ngi∈NGB，ngi的邻域粒离群度为：

(8)

定义 6.对于任何对象xi∈U，xi的基于邻域粒的离群因子定义为：

(9)

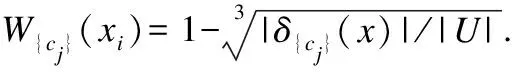
权重函数W{cj}符合这样的观点，即离群点检测总是涉及数据集中的少数对象，并且这些对象更可能是离群点.从公式(9)中可以看出，权重越高，基于邻域粒的离群因子越大，因此，对于∀xi∈U和cj∈C，如果邻域粒δ{cj}(xi)的基数小于其他邻域粒的基数，那么将xi视为属于U中的少数对象，并为xi赋予高权重.如果xi的离群因子越高，那么xi越可能是离群点.

定义 7.设μ是一个给定的阈值，对任意xi∈U，如果NGOF(xi)>μ，则把xi称为基于邻域粒的离群点.

3.3 检测算法

算法1.基于邻域粒的离群点检测算法(NGOD)

输入：信息系统IS=(U，C，V，f)，阈值μ

输出：离群点集(Outlier Set，OS)

1.OS←∅

2.对任意x，y∈U，计算NOM(x，y)

3.forj←1tomdo

4. 计算邻域粒族{δ{cj}(xi)|xi∈U}

5. 构建NG{cj}={ng1，ng2，…，ngk}

6.endfor

7.forj←1tomdo

8.fori←1tokdo

9.forr←1tokdo

10. 计算M(ngi，ngr)

11.endfor

12.endfor

13.endfor

14.fori←1tondo

15.forj←1tomdo

16. 计算GOD(δ{cj}(xi))

17. 计算W{cj}(x)

18.endfor

19. 计算NGOF(xi)

20.ifNGOF(xi)>μthen

21.OS←OS∪{xi}

22.endif

23.endfor

24.returnOS

算法1通过 “for”循环的获得离群点集，步骤(2)的频度为n×n，步骤(3)-步骤(6)的频度为m，步骤(4)的频度为n×n，步骤(7)-步骤(13)的频度为m，步骤(8)-步骤(12)的频度为k，步骤(9)-步骤(11)的频度为k，步骤(14)-步骤(23)的频度为n，步骤(15)-步骤(18)的频度为m.从而，算法1总的频度为n×n+m×n×n+m×k×k+m×n.因此，在最坏的情况下，算法1的时间复杂度为O(mn2)，空间复杂度为O(mn).

4 数据实验

在本节中，为了评估NGOD算法的有效性，选取了三个数据集(包括数值、分类和混合属性)进行实验[21].为了形成一个非常不平衡的分布，本文使用文献[3，8]中的实验技术对数据集进行预处理，最后的数据预处理和描述如表1所示1.在三个数据集上，本文比较了NGOD算法与GrC、FindCBLOF、LOF、DIS和KNN算法的性能.如表2所示，描述了六种比较算法及其优缺点.

4.1 实验设置

在实验中，对于GrC算法，使用重叠距离量度来计算两个粒之间的距离，对于Cr数据集，GrC算法需要的参数d为|C|/4，另外两个数据集的实验结果参考文献[8].本文对三个数据集重复LOF和KNN算法，分别计算其参数MinPts和K在1～n范围内的最优参数.对于LOF算法，Cr，Ly和Wi数据集的最优参数MinPts分别设置为：197、36和15.对于KNN算法，Cr、Ly和Wi数据集的最优参数K分别设置为：33、27和39.对于Cr数据集，FindCBLOF算法所需的三个参数α、β和s分别设置为90%、5和5，而对于Ly和Wi数据集的实验结果参考文献[3].此外，对于所有基于粗糙集的方法，Ly和Wi数据集中的所有属性值均被认为是分类类型[3，8].

表1 最终数据的预处理和描述
Table 1 Final data preprocessing and description

数据集缩写预处理对象数数值属性分类属性离群点数正常点数Credit ApprovalCr忽略有一个或多个缺失值的37个对象,然后从剩余的653个对象中删除271 “+”个对象,类“+”被看作离群点.3826925357LymphographyLy类“1”和“4”被看作离群点.1483156142Wisconsin Breast CancerWi删除202个“malignant”对象和14个“benign”对象,“malignant”类被看作离群点.4839039444

表2 六种比较算法的优缺点
Table 2 Advantages and disadvantages of six comparison algorithms

算法(参考文献)策略优 点缺 点NGOD(本文)基于邻域粒的最优的混合距离度量和合理的半径设置,邻域粒的不确定性,适用于分类、数值和混合属性数据.需要计算更多的邻域关系,只考虑单个属性的信息.GrC(文献[7])基于粒计算的粒化能力强,适用于分类属性数据.数值数据需离散化预处理,不适用于数值属性数据.FindCBLOF(文献[3])基于聚类的与经典聚类相结合,适用于分类属性数据.检测效果差,不适用于数值属性数据.LOF(文献[5])基于密度的适用于数值属性数据.不适用于分类属性数据.DIS(文献[4])基于距离的简单且适用于数值属性数据.不适用于分类属性数据.KNN(文献[20])K-近邻适用于数值属性数据.不适用于分类属性数据.

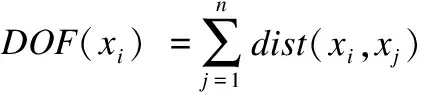
4.2 实验评估

对于所有的算法，通过Aggarwal和Yu引入的评估方法来评估它们的性能[5].它主要包括“顶比率(对象数)”和“属于离群点的个数(覆盖率)”.首先，六种离群点检测算法被用来计算每个对象的离群因子.然后，所有对象通过离群因子升序排列，令OStopk(U)表示U中排序前k个对象的集合，OStrue(U)表示在U中真实离群点的集合.所以，对于每个算法，对象数等于|OStopk(U)|，属于离群点的个数等于|OStopk(U)∩OStrue(U)|.而顶比率(Top Ratio，TR)和覆盖率(Coverage Ratio，CR)计算如下：

(10)

(11)

显然，当TR(k)一定时，CR(k)越大，算法的性能越好.使用这个方法，NGOD算法的参数仅需λ.

4.3 实验结果分析

三个数据集的所有数据都分别被导入信息系统ISCr，ISLy和ISWi.则有：|UCr|=382，OStrue(UCr)=25;|ULy|=148，OStrue(ULy)=6;|UWi|=382，OStrue(UWi)=39.对于NGOD算法，ISCr，ISLy和ISWi的参数分别设为λCi=0.8，λLy=0.2，λWi=1.4.实验结果如表3～表5所示.

表3ISCr中的对比实验结果
Table 3 Comparative experimental results inISCr

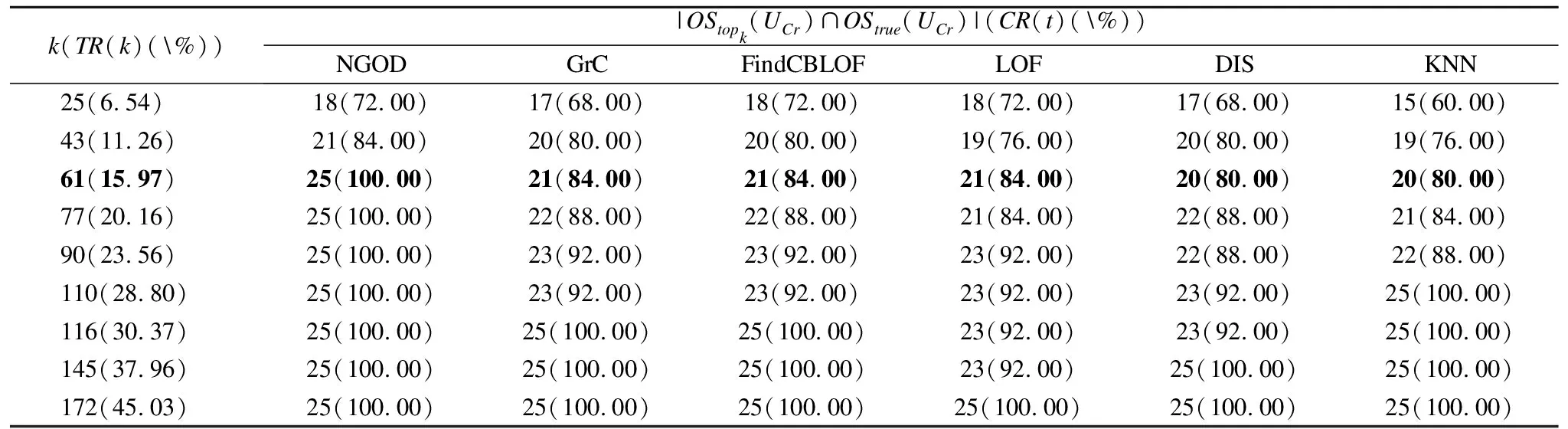
k(TR(k)(\%))|OStopk(UCr)∩OStrue(UCr)|(CR(t)(\%))NGODGrCFindCBLOFLOFDISKNN25(6.54)18(72.00)17(68.00)18(72.00)18(72.00)17(68.00)15(60.00)43(11.26)21(84.00)20(80.00)20(80.00)19(76.00)20(80.00)19(76.00)61(15.97)25(100.00)21(84.00)21(84.00)21(84.00)20(80.00)20(80.00)77(20.16)25(100.00)22(88.00)22(88.00)21(84.00)22(88.00)21(84.00)90(23.56)25(100.00)23(92.00)23(92.00)23(92.00)22(88.00)22(88.00)110(28.80)25(100.00)23(92.00)23(92.00)23(92.00)23(92.00)25(100.00)116(30.37)25(100.00)25(100.00)25(100.00)23(92.00)23(92.00)25(100.00)145(37.96)25(100.00)25(100.00)25(100.00)23(92.00)25(100.00)25(100.00)172(45.03)25(100.00)25(100.00)25(100.00)25(100.00)25(100.00)25(100.00)

由表3可见，对于信息系统ISCr，NGOD算法明显要好于其他算法.例如，当k=61时，NGOD算法能检测出全部真实离群点，其覆盖率为100.00%.然而，对于GrC、FindCBLOF、LOF、DIS和KNN算法，其覆盖率分别为84.00%、84.00%、84.00%、80.00%和80.00%，比NGOD算法低.更多的是Cr数据集为混合属性数据.因此，我们可以得到NGOD算法适用于混合属性数据.

表4ISLy中的对比实验结果
Table 4 Comparative experimental results inISLy

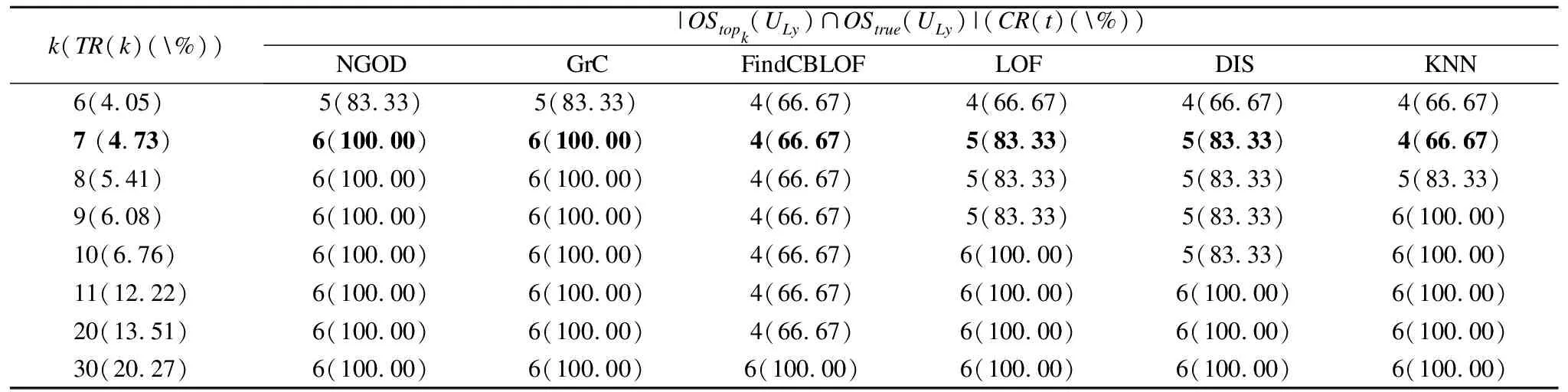
k(TR(k)(\%))|OStopk(ULy)∩OStrue(ULy)|(CR(t)(\%))NGODGrCFindCBLOFLOFDISKNN6(4.05)5(83.33)5(83.33)4(66.67)4(66.67)4(66.67)4(66.67)7 (4.73)6(100.00)6(100.00)4(66.67)5(83.33)5(83.33)4(66.67)8(5.41)6(100.00)6(100.00)4(66.67)5(83.33)5(83.33)5(83.33)9(6.08)6(100.00)6(100.00)4(66.67)5(83.33)5(83.33)6(100.00)10(6.76)6(100.00)6(100.00)4(66.67)6(100.00)5(83.33)6(100.00)11(12.22)6(100.00)6(100.00)4(66.67)6(100.00)6(100.00)6(100.00)20(13.51)6(100.00)6(100.00)4(66.67)6(100.00)6(100.00)6(100.00)30(20.27)6(100.00)6(100.00)6(100.00)6(100.00)6(100.00)6(100.00)

表5ISWi中的对比实验结果
Table 5 Comparative experimental results inISWi

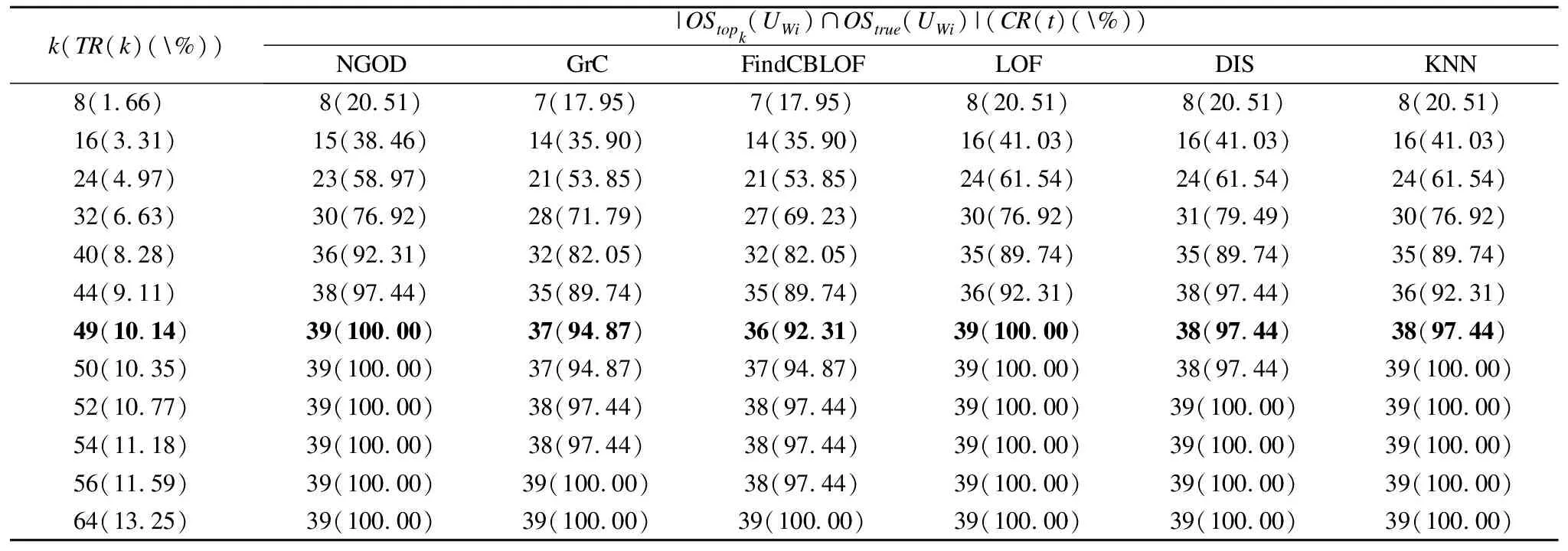
k(TR(k)(\%))|OStopk(UWi)∩OStrue(UWi)|(CR(t)(\%))NGODGrCFindCBLOFLOFDISKNN8(1.66)8(20.51)7(17.95)7(17.95)8(20.51)8(20.51)8(20.51)16(3.31)15(38.46)14(35.90)14(35.90)16(41.03)16(41.03)16(41.03)24(4.97)23(58.97)21(53.85)21(53.85)24(61.54)24(61.54)24(61.54)32(6.63)30(76.92)28(71.79)27(69.23)30(76.92)31(79.49)30(76.92)40(8.28)36(92.31)32(82.05)32(82.05)35(89.74)35(89.74)35(89.74)44(9.11)38(97.44)35(89.74)35(89.74)36(92.31)38(97.44)36(92.31)49(10.14)39(100.00)37(94.87)36(92.31)39(100.00)38(97.44)38(97.44)50(10.35)39(100.00)37(94.87)37(94.87)39(100.00)38(97.44)39(100.00)52(10.77)39(100.00)38(97.44)38(97.44)39(100.00)39(100.00)39(100.00)54(11.18)39(100.00)38(97.44)38(97.44)39(100.00)39(100.00)39(100.00)56(11.59)39(100.00)39(100.00)38(97.44)39(100.00)39(100.00)39(100.00)64(13.25)39(100.00)39(100.00)39(100.00)39(100.00)39(100.00)39(100.00)

对于表4和表5，可以做同样的分析，当k分别为7和49时，得到NGOD算法同样优于或等于其它算法的结论.Ly数据集的属性大多数为符号属性，而Wi数据集的属性为数值型属性.因此，NGOD算法也适用于符号属性和数值属性数据.

5 结 论

本文在邻域粗糙集的框架下提出了一种基于邻域粒的离群点检测，并给出了相应的检测算法，该算法充分利用邻域粗糙集能处理多种数据类型的特性，可以在不确定数据中挖掘出多样属性类型的离群点.最后，通过数据实验对比分析，所提的算法是有效的，能适用于数值、分类和混合属性数据.在未来的研究工作中，还可以采用其他粗糙集模型来构建离群点检测方法，如模糊粗糙集、优势粗糙集等.