NO TEARS算法在XSS攻击检测中的应用研究

孙宝丹，王培超，周 鋆

1(国防科技大学 信息系统工程重点实验室，长沙 410072)2(中国人民解放军31104部队，南京 210018)

1 引 言

XSS(Cross-Site Scripting)全称跨站脚本，是一种常见的Web应用漏洞.XSS攻击属于用于客户端的被动式攻击方式，所以危害性容易被忽视.攻击者在Web页面里插入恶意脚本代码，当用户浏览该页时，嵌入Web页面里的恶意脚本代码就会被执行，从而达到恶意攻击用户的目的[13].XSS漏洞可以分为三类：Stored XSS漏洞、Non-persistent XSS漏洞以及DOM-Based XSS漏洞[13].XSS漏洞会给企业带来巨大的经济损失，利用XSS攻击，攻击者可以获取用户隐私、盗取用户身份Cookie、劫持用户的浏览器等，会给用户带来严重的生活困扰.目前虽然已经有一些检测XSS攻击的方法，但是这些方法的效果有限.因此，如何高效检测XSS攻击仍然是一个需要深入研究的问题，本文将机器学习方法与XSS攻击检测相结合，实现了对XSS攻击的有效检测.

利用机器学习方法进行XSS检测目前已有一定的应用，其中包括：Gupta MK[1]等人将XSS漏洞检测转换为基于预测模型的分类问题，并提出了一种基于文本挖掘和模式匹配的新方法；Khan Nayeem[2]等提出了一种将一组有监督和无监督分类器作为在客户端使用的拦截器来检测恶意脚本的方法；Sunder NS[3]等提出了一种先进的XSS预测方法，引入新的评分系统对浏览器中的内容确定特权级别和漏洞级别，同时使用机器学习算法存储，分类和分析在浏览器中运行的Java脚本.

GuoXiaobing[4]等利用机器学习算法构建了优化模型，减小了攻击媒体库的大小，提高了XSS漏洞检测的效率；RathoreShailendra[5]等人用多种分类器区分网页是否受到XSS攻击；Angelo Eduardo Nunan[6]提出了从Web文档内容和URL中提取特征，并使用机器学习技术在网页上进行XSS自动分类；Xi Xiao[7]等介绍了一种对基于编码的注入攻击进行检测的方法，该攻击方式比一般注入攻击更加隐蔽，其中的JavaScript代码以人类不可读的形式编码，文中使用机器学习的分类算法来确定应用程序是否遭受代码注入攻击.贝叶斯网络作为一种解释性很强的机器学习模型，也可以很好应用到XSS检测中，目前有Zhou Yun[8]等使用集成贝叶斯网络的方法进行XSS攻击检测，但在模型结构获取时采用的是传统的贝叶斯网络结构学习算法.

本文中使用的NO TEARS算法[9]区别于以往的贝叶斯网络学习算法，不需要深入了解图论的相关知识，将本来复杂的结构学习算法转化为较为容易求解的数值优化问题.与基于局部启发式的结构学习算法不同，NO TEARS能够找到全局最优的有向无环图结构，利用更优的模型对XSS攻击进行检测，从而可以在检测中达到更高的准确率.算法中主要通过定义一个新的无环性的描述方法，将非凸组合约束项转化为容易求解梯度值的平滑函数，只涉及一些基本的矩阵运算，求解容易，工程化难度较低.

本文利用NO TEARS算法获取的贝叶斯网络作为分类器，对XSS攻击载荷(Payload)进行检测，其主要贡献有：1)将NO TEARS算法应用到XSS攻击检测领域，验证了NO TEARS算法在实际应用过程中的有效性；2)使用机器学习方法实现了对XSS攻击进行自动检测；3)本文中设计算法模型与其他模型相比取得了较高的准确率.

本文的创新点主要如下：1)本文使用的结构学习算法能够寻找全局最优的贝叶斯网络结构；2)首次将这种算法应用到网络安全领域关注的重要问题—XSS攻击检测，并取得很好的实验结果，具有一定的参考及应用价值.

2 XSS检测问题描述

要将NO TEARS算法应用到XSS检测中，首先要获取XSS攻击的特征，这里涉及对XSS攻击载荷的特征提取[8].根据XSS攻击的特点，本文从以下几个方面选取特征：1)输入长度；2)XSS攻击载荷常见的敏感关键词和敏感字符；3)跳转链接对应的协议(protocol)出现的次数.经过筛选，本文将一条记录用30个特征进行表示，这些特征从1开始编号到30，同时节点31代表标签，表示当前记录是否为XSS攻击，具体特征如表1所示.

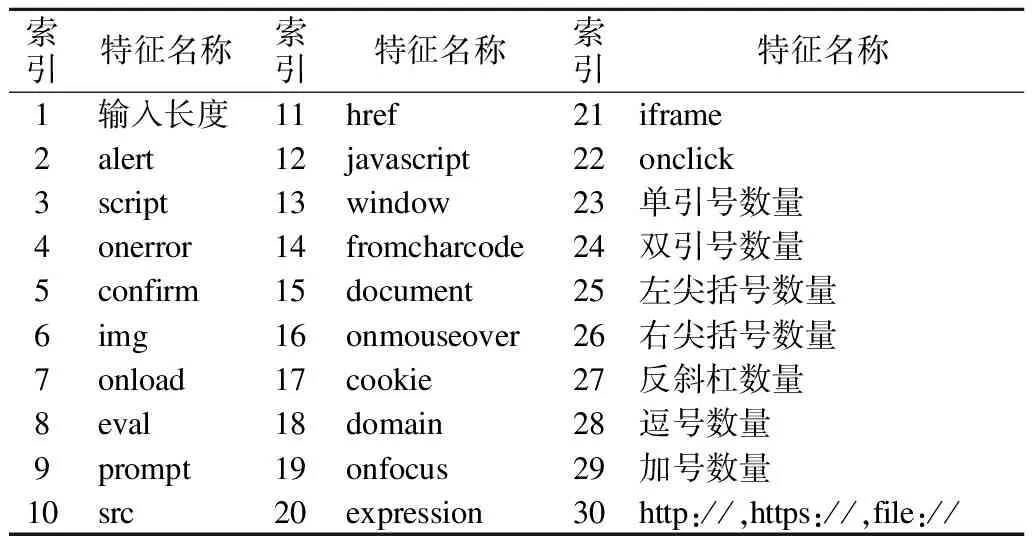
表1 XSS攻击特征Table 1 Features of XSS attack

攻击特征获取之后，便可以建模对XSS攻击进行检测，如图1所示.这里在将数据输入到分类器之前，首先要对数据进行预处理.攻击者对用户发动XSS攻击时，会将XSS payload进行隐藏，诸如使用大小写变换或编码转换等，因此需要对数据进行相关解码，解码依照如下顺序：变小写、URL解码、HTML解码、JavaScript解码、Unicode解码、URL二次解码.数据完成解码之后，对于每一条记录，可以获取相应特征的值，特征已经在上一节列出.最后把处理后的数据输入到贝叶斯网络结构学习算法中，通过结构学习获取更优的贝叶斯网络模型，并基于此对样本进行检测，输出相应的分类标签.

3 贝叶斯网络结构学习

前文提到过，有向无环图的结构学习是一个NP难的问题，现有的结构学习算法都不能有效实现无环约束.这是由于无环约束是组合约束，同时它的计算规模随节点数呈超指数增加.另外，即便能够得到相对满足约束条件的有向无环图，它也不一定适合一般目的的优化.目前的结构学习算法依赖于不同的局部启发式算法，这种方法虽然能够降低计算规模，但是不能得到全局最优的结构.现有的算法大致有分支-切割法、动态规划法、A*搜索法、贪心算法、坐标下降法等[10].与这些算法不同，本文应用的算法采用完全不同的求解方法，将原本的结构优化问题，转化成数学优化问题进行求解.值得注意的是，这里得到的解是针对当前数据得到的全局最优的贝叶斯网络结构，相比传统启发式算法有了很大的提升.同时这里使用的算法不要求研究人员具有很深的图论基础，从而具有广泛的研究和应用价值.

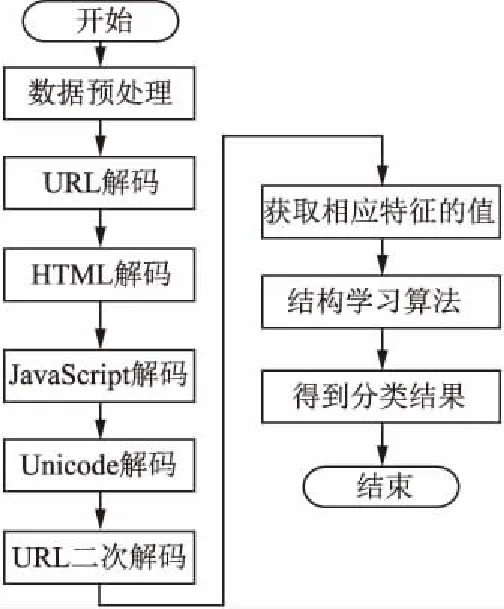
图1 XSS检测过程Fig.1 Process of XSS attack detection

3.1 贝叶斯网络结构的数学表示

本文中使用的算法是一种新的描述贝叶斯网络的方法，通过求解一个带有平滑约束的优化问题，从而找到最优的有向无环图.具体地，对于任意给定数据集W=(wij)∈d×d，令A(W)∈{0，1}d×d是一个表示有向图的二元邻接矩阵，那么有如下描述：[A(W)]ij=1⟺wij≠0，反之则相反.同时D⊂{0，1}d×d表示二元矩阵B的子集，其中B是无环图的邻接矩阵，那么贝叶斯结构优化问题转换成如下的非凸形式：

(1)

其中Q是与数据有关的损失函数，X∈n×d是数据矩阵，h是一个平滑函数，h：d×d→只有当A(W)∈D时，h(W)=0.那么上述基于图论表示的贝叶斯网络的结构，就转化成这样一个非凸优化的问题，可以根据数学优化的工具进行求解.但是在正式求解前，需要将上式中的无环约束进行进一步的刻画，用数学方法表示出来，才能便于后续优化问题的求解.

3.2 无环约束的表示方法

这一部分主要介绍一种新的无环约束的表示方法，这里使用了矩阵指数的概念，便于后续优化问题的求解.矩阵指数是所有方块阵都能定义的一类函数，类似于指数函数.在表示方法上将指数函数的变量用方块矩阵代替，具体定义方式如下：

(2)

值得注意的是这里，B为n×n的实数或复数矩阵，那么就有这样的定理：

定义1.当且仅当trexp(B)=d时，B∈{0，1}d×d是有向无环图的邻接矩阵.

证明：当且仅当(Bk)ii=0对所有的k≥1和所有i都成立时，B表示在有向图中不存在环路，那么就有：

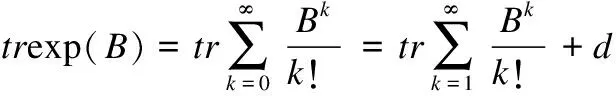
(3)

鉴于上述定理中使用的方块矩阵B，且B同时也是个二元矩阵，不能普遍适用于一般数据，因此接下来应该找到一种可以将B替换成任意权重矩阵W的方法，这里使用的是矩阵的Hadamard乘积，定义为：

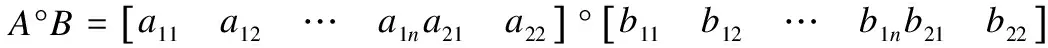
(4)

其中A，B∈m×n且A={aij}，B={bij}，均为m×n的矩阵.经过如上的变换，对于给定任意权重矩阵W∈d×d，无环约束就可以表示为：

h(W)=trexp(W°W)-d=0

(5)

h(W)的梯度值为：

h(W)=[exp(W°W)]T°2W

(6)

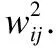
4 NO TEARS算法

4.1 无环约束优化问题

之前已经给出过贝叶斯网络的数学表达方式，并对其中的无环约束进行了数学变换，得到最终需要进行优化的数学表达式：

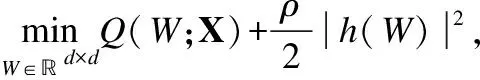
(7)

这里引入了一个二次惩罚项ρ>0表示惩罚违反约束h(W)=0，那么上式就可以使用增广拉格朗日法进行求解，带有对偶变量α的增广拉格朗日方法可以写作：

(8)

它的对偶形式为：

(9)

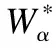
(10)

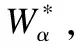
(11)

这里的步长ρ的大小是比较增广问题和初始约束问题得来的，这两个表达式的梯度分别如下所示：

▽Q(W；X)+[α+ρh(W)]▽h(W)=0

(12)

▽Q(W；X)+α▽h(W)=0

(13)

4.2 算法流程及后处理过程

根据上述无约束优化问题的求解过程，最终可以得到本文中使用的新的贝叶斯网络结构学习算法的总体流程如表2所示.需要注意的是在上文指出了对于无环约束的表示方法为h(W)=0，但在算法中设置的优化准确率ε>0，且是一个非常接近于0的值.这样带来一个问题，虽然最终的结果是一个非常接近有向无环图的网络，但仍然无法保证得到的是满足约束条件的有向无环图.因此这里引入一个后处理的过程：定义B(ω)=I(W>ω)，且找到满足定义的最小阈值ω*>0，就能够得到有向无环图，这里I(·)是指示函数.

表2 增广拉格朗日方法Table 2 Augmented lagrangian algorithm

5 实验结果与分析

5.1 实验设置

XSS Payload 的训练集从GitHub 上获取而来，其具有151658 条记录，包含16151 条黑样本(XSS Payload)和135507条正常URL[8].测试集包含了从GitHub和各大安全博客论坛上收集的Payload，共有10000条记录，包含6503条正常样本和3497条黑样本.实验中使用Python集成环境Anaconda3，Python版本为3.6，同时应用NO TEARS相应的Python算法包.为了验证本文中使用的结构学习算法的效果，这里设置对比实验，即将本文中使用的算法与目前效果较好的基于局部搜索和评分函数的结构学习算法(Tabu Search)[11]、Greedy Hill Climbing[12]算法使用相同的训练集和测试集进行实验，并比较它们分类的准确性.本文设置的另一组对比实验为：将本文使用的NO TEARS算法与现有的其他分类算法—朴素贝叶斯分类器(Naïve Bayes，NB)、逻辑回归(Logistics Regression，LR)、决策树(Decision Tree，DT)和随机森林(Random Forest，RF)算法——进行比较.两组实验均设定训练样本数取训练集中数据的55%、60%、65%、70%，并取上述不同分类算法的准确率.

5.2 实验结果及分析

从表3中可以看出，本文中使用的NO TEARS算法的准确率普遍在98.35%以上，比Tabu Search和Greedy Hill Climbing算法都要高，这是因为NO TEARS算法求解出来的是贝叶斯网络的全局最优结构，因此分类的结果更加准确.随着表格中训练样本数的增加，算法的分类准确率也在不断增大，当样本数达到训练集的70%时，即使用105461条数据进行训练时，准确率可以达到98.56%，远超传统的结构学习算法，显示出了优越的性能.

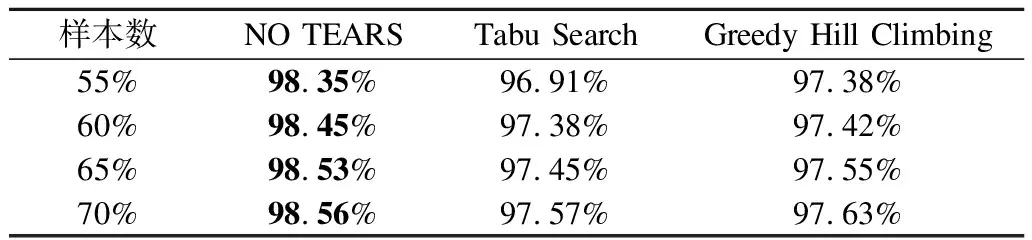
表3 不同贝叶斯结构学习算法的准确率比较Table 3 Accuracy of different BN structure learning algorithms

本文中采用的NO TEARS算法与传统的基于评分和局部搜索的算法不同，是一个能够找到全局最优解的算法.基于评分和局部搜索的贝叶斯网络结构学习算法，虽然能够有效减少解空间的规模，但是并不能保证找到全局最优的网络结构.而NO TEARS算法能够找到全局最优的网络结构，构建的贝叶斯网络分类器结构更优，其准确率故而要高于一般的结构学习算法.

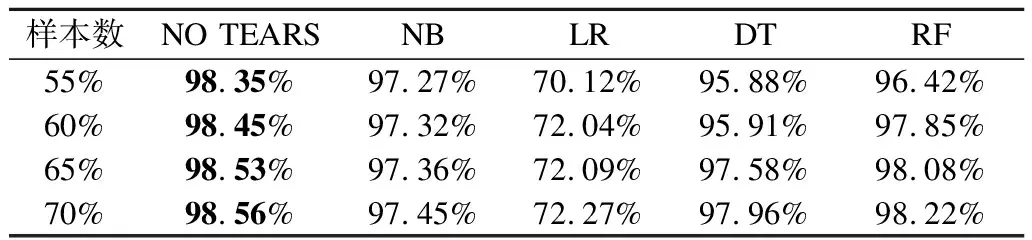
表4 不同分类器算法的准确率比较Table 4 Accuracy of different classifier algorithms

从表4中可以看出，本文中使用的NO TEARS算法的效果均优于表中其他算法.同时，逻辑回归在这些算法中分类准确率最低，在70%左右，而其余算法的准确率均在95%以上，分类效果相对其他算法较差.

6 结 论

网络空间安全如今日益受到关注，Web安全是其中的重要方面，本文选择应用层常见漏洞XSS，引入了机器学习中的贝叶斯网络的结构学习算法，用于检测XSS攻击载荷是否存在.贝叶斯网络目前在多领域均具有广泛应用，其结构学习算法较为复杂，是一个NP难的问题.尽管目前在贝叶斯网络的结构学习方面取得了进步，其仍然受到多方面条件的制约.本文中使用的NO TEARS算法，不同于一般的结构学习算法，能够找到全局最优的结构，因此大大增加了分类准确率.本文首先介绍了对XSS攻击及其类别，然后介绍了机器学习和贝叶斯网络在XSS检测领域的相关研究以及文中使用的NO TEARS算法.接着，本文给出了XSS检测问题的描述，在将原始数据输入到分类器之前，首先要对数据进行预处理，文中对数据共进行5种预处理方式，将处理之后的数据依据特征进行相应值的提取并将提取值输入算法，经过算法学习之后就可以得到用于判断的分类器.然后本文具体描述了使用的全局优化算法，给出了其原理、公式以及算法流程.最后本文对使用的算法进行了实验，实验结果表明利用传统贝叶斯结构学习算法得到的网络进行分类最高可达97.63%的准确率，而NO TEARS算法能够达到98.56%的准确率，优于传统的结构学习算法和其他经典分类算法，更加有效地实现了对于XSS攻击载荷的检测.