融合用户偏好和物品相似度的概率矩阵分解推荐算法

王 运，倪 静

(上海理工大学 管理学院，上海 200093)

1 引 言

近年来，随着互联网的迅猛发展，人们面临的信息量呈指数级增长，个性化推荐算法在人们的日常生活中拥有越来越重要的地位.传统的推荐算法主要有协同过滤推荐算法[1]、基于内容的推荐算法[2]、基于图模型的推荐算法[3]等，这些推荐算法利用用户与物品数据取得了一定的推荐效果，如文献[4]利用用户及物品数据计算用户的偏好模型，在计算出用户之间的偏好相似度后进行协同过滤推荐；文献[5]将用户与物品之间的关系进行图形化描述，通过计算目标用户与物品之间连边的相关性大小进行推荐；文献[6]通过用户之间的社交关系数据计算用户之间的相似度值，进而根据所得用户相似度值进行推荐.但是这些推荐算法也面临着许多问题，如用户数据稀疏性问题.当推荐系统中出现新用户时更为显著，由于用户数据的稀疏性，计算所得用户相似度值不够准确或者根本无法计算出新用户与其他用户之间的相似度，最终导致算法的评分预测准确性有所降低.

同时，在2006年的Netflix竞赛中，有人将矩阵分解技术应用到用户电影评分矩阵中，并且提升了评分预测的准确性[7].从此关于矩阵分解的推荐算法研究在不断增多，如考虑到用户评分习惯的不同，有专家学者提出了BiasSVD算法，通过在矩阵分解中融入用户或者物品的偏置因素提高了评分预测准确性[8]；由于用户的隐私反馈也会对推荐算法产生影响，文献[9]将基于领域的推荐算法和BiasSVD进行融合，提出了SVD++；文献[10]提出概率矩阵分解模型，在矩阵分解的过程中融入概率论相关知识，具有较好的可解释性和评分预测准确性.

基于上述研究成果，本文提出了融合用户偏好和物品相似度的概率矩阵分解推荐算法UPIS-PMF(Probability Matrix Factorization Recommendation Algorithm Combining User Preferences and Item Similarity)，该算法在概率矩阵分解技术处理用户物品评分矩阵的同时融入了用户偏好信息及物品信息，通过用户信息及物品信息计算用户相似度矩阵及物品相似度矩阵，从而更好的预测出用户特征矩阵及物品特征矩阵，最终提高评分预测的准确性.Movielens数据集中的实验表明该算法有效的缓解了用户数据稀疏性问题，在评分预测准确性方面相比传统推荐算法有一定的提升.

2 相关工作

由上文可知，传统推荐算法在应用的过程中经常面临数据稀疏的缺点，而矩阵分解技术可以缓解数据稀疏性问题，并提高评分预测的准确性.矩阵分解技术主要分为SVD矩阵分解(Sigular Value Decomposition)、概率矩阵分解PMF(Probability Matrix Factorization)和非负矩阵分解NMF(Non-negative Matrix Factorization).在概率矩阵分解模型中融入用户信息可以提高分解后用户特征矩阵的准确度，如文献[11]将用户社交信息融入概率矩阵分解模型中，通过用户社交信息可以计算出用户的社交相似度，并且能够提高矩阵分解后用户特征矩阵的准确度，进而提高评分预测准确性；文献[12]通过整合社交网络中的用户信任关系得到用户信任矩阵，将用户信任矩阵融入概率矩阵分解模型中提高了矩阵分解的准确度和评分预测准确性.

通常而言，计算用户相似度不仅可以利用社交信息或者信任信息，根据用户的偏好信息也可以计算出相应的用户相似度值，如文献[13]正是利用用户评分数据及物品数据计算出用户的偏好信息，再根据用户偏好信息计算用户之间的相似度值，最后根据用户相似度进行协同过滤推荐，并通过实验证明了这种方法很有效.所以，当用户数据中不包含社交及信任等信息时，可以根据用户偏好寻找用户之间的关系并将其融入概率矩阵分解模型中，以提高分解后用户特征矩阵的准确度.另一方面，物品信息通常包括物品标签数据及物品流行度数据等，根据这些数据可以计算出物品之间的相似度值，将物品相似度矩阵融入概率矩阵分解模型中也会提高物品特征矩阵的准确度.

因此，本文利用概率矩阵分解技术在处理用户物品评分矩阵时的优势，同时寻找用户之间的关系和物品之间的关系，将用户相似度矩阵和物品相似度矩阵共同融入概率矩阵分解模型，可以从用户及物品两个角度提高对应特征矩阵的准确度，最终提高评分预测的准确性.

3 概率矩阵分解模型

基于概率矩阵分解的推荐算法是在传统基于矩阵分解推荐算法的基础上融合概率论相关知识，从概率的角度出发解释与计算矩阵分解技术，使得算法的可解释性得到了提升，同时评分预测准确性也有所提高.

如表1所示为本文算法所用符号及对应解释.

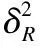
表1 数学符号
Table 1 Mathematical notations

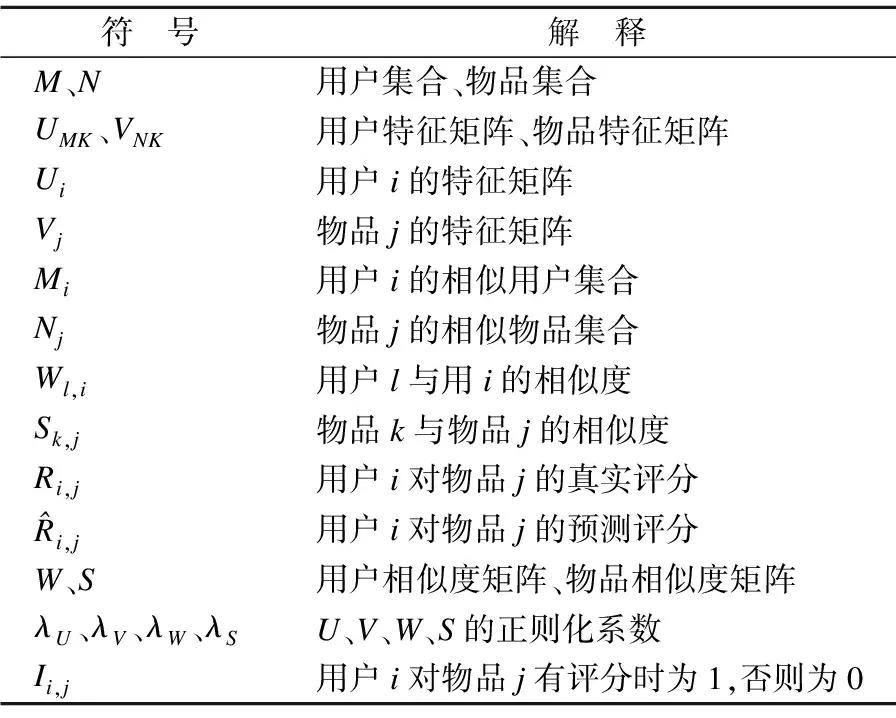
符 号解 释M、N用户集合、物品集合UMK、VNK用户特征矩阵、物品特征矩阵Ui用户i的特征矩阵Vj物品j的特征矩阵Mi用户i的相似用户集合Nj物品j的相似物品集合Wl,i用户l与用i的相似度Sk,j物品k与物品j的相似度Ri,j用户i对物品j的真实评分^Ri,j用户i对物品j的预测评分W、S用户相似度矩阵、物品相似度矩阵λU、λV、λW、λSU、V、W、S的正则化系数Ii,j用户i对物品j有评分时为1,否则为0

(1)

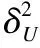
(2)

(3)

由贝叶斯公式可得U与V的概率分布函数如公式(4)所示：

p(U,V|R)∝p(U,V,R)=p(R|U,V)p(U)p(V)

(4)

最大化公式(4)可得公式(5)所示目标函数：

(5)

4 UPIS-PMF算法

4.1 算法原理

根据本文前几节可知，将概率矩阵分解模型应用在推荐系统的用户物品评分矩阵中会有显著的效果，在评分预测准确性方面优于传统推荐算法.同时，对目标矩阵进行矩阵分解会形成用户特征矩阵和物品特征矩阵，如果这两个特征矩阵的值更为准确，最终的评分预测准确性也会相应提高.近几年，有许多专家学者从用户角度出发，如利用用户社交信息，用户信任信息等，通过用户的相关数据计算用户之间的相似度，将相似度矩阵融入概率矩阵分解模型中进而可以提高用户特征矩阵的准确度，另一方面，如果可以找到物品之间的关系，将相应的物品相似度矩阵融入概率矩阵分解模型中，则自然也可以提高物品特征矩阵的准确度.

如图1为UPIS-PMF算法模型示意图.

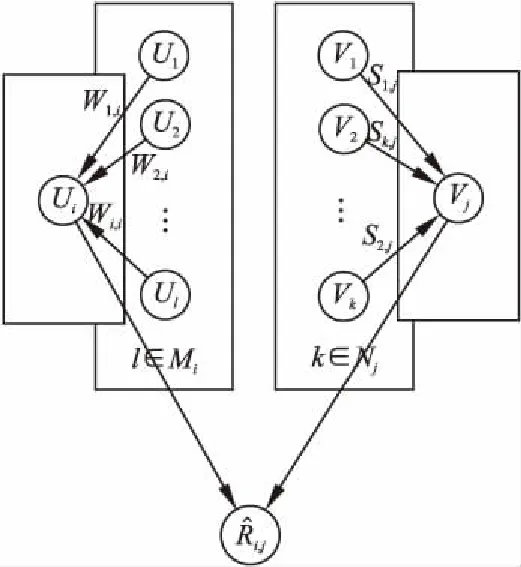
图1 UPIS-PMF算法模型示意图Fig.1 Schematic diagram of UPIS-PMF algorithm model

图1中，用户i的特征向量受到相似用户l∈Mi的影响，物品j的特征向量受到相似物品k∈Nj的影响，在本文的UPIS-PMF算法中，可以利用用户偏好数据计算出用户之间的相似度，利用物品标签关联度和物品流行度数据计算物品之间的相似度，根据修正后的用户向量和物品向量计算出的用户物品评分会更加准确.

4.2 基于用户偏好相似度的用户模型

在推荐系统中，用户对许多物品存在评分行为，而物品通常带有标签属性，根据评分数据及物品标签数据可以计算出用户对标签的评分，即为用户偏好，如果用户对某一标签有多次评分，则取为平均值.

对于用户i与用户l，有公式(6)所示用户偏好相似度计算公式：

(6)

公式(6)中，t∈Ti∩Tl为用户i与用户l的共同标签评分集合，ri,t、rl,t分别为用户i、用户l对标签t的评分，该公式考虑到了用户评分偏好对结果的影响，将标签评分与平均评分的差值作为修正后的评分参与计算，最终计算出的相似度会更为准确.

由于用户的特征受到相似用户的影响，则对于用户i，有公式(7)所示公式：

(7)

将公式(7)以矩阵形式进行描述可转化为公式(8)所述形式：

(8)

(9)

所以，融合用户偏好相似度的用户潜在特征向量的概率分布如公式(10)所示：

(10)

4.3 基于物品相似度的物品模型

在研究推荐算法的道路中，许多专家学者都专注于用户角度，利用用户之间的关系进行推荐或者评分预测，而物品之间也存在一定的关系，将物品关系融入推荐算法也可以提高评分预测准确性.

在推荐系统中，物品通常具有标签关联度数据及物品流行度数据等，标签关联度即为物品与标签之间的关联程度，物品流行度指的是物品流行程度，比如淘宝中物品的点赞数量、豆瓣电影评分等.如果两个物品的标签关联度数据很相似，那么这两个物品的相似度会很高，同时，相似物品的流行程度也会很接近.

令物品j与物品k对标签t的关联度数据分别为realte(j,t)、realte(k,t)，则对于这两个物品有公式(11)所示物品标签相似度计算公式：

(11)

公式(11)中，Tk∩Tj为物品k与物品j的共同标签集合.同时，推荐系统中的物品通常具有流行程度，且流行度可以进行数字量化表示，令物品j与物品k的流行度分别为popj和popk，则物品j与物品k关于流行度的相似度计算公式如公式(12)所示：

(12)

由于两个物品的流行度仅为单独的数字，没有共同部分，所以不能采用类似公式(11)的公式，而是采用公式(12)这种指数函数形式，同时，考虑到两个流行度都很高的物品流行度差值也可能很高，如点赞数都是几十万级别，采用了相对流行的计算方式，将流行度差值的绝对值与最大流行度相除作为指数函数的自变量，使得相似度值计算结果更准确.

利用公式(11)与公式(12)所得相似度值可以计算物品的综合相似度，计算公式如公式(13)所示：

Sk,j=β*sim(k,j)pop*sim(k,j)tag

(13)

公式(13)中，β为参数，用以调整标签相似度与流行度相似度乘积对结果的影响，采用公式(13)而不是传统加权的方式，可以最大限度的保证只有物品的标签数据相似且流行度相似时最终的相似度值才会很高.

同4.2，对于物品Vj，有公式(14)：

(14)

(15)

所以，融合物品相似度的物品潜在特征向量的概率分布如公式(16)所示：

(16)

4.4 UPIS-PMF模型

由4.1、4.2及4.3可知，融合用户偏好相似度矩阵、物品相似度矩阵和概率矩阵分解模型可得如公式(17)所示后验概率公式：

(17)

最大化上述概率时，可得如公式(18)所示目标函数：

(18)

(19)

(20)

对Ui与Vj进行梯度下降法迭代时满足公式(21)及公式(22)：

(21)

(22)

公式(21)与公式(22)中，α为学习速率，用以控制用户特征向量与物品特征向量在每次迭代时取值变化的大小，当迭代结束时即可得到相应用户特征矩阵和物品特征矩阵，也可预测出任何用户对任何物品的评分.

4.5 算法步骤

本文的算法主要分为输入输出两步：

输入：用户物品评分矩阵R、用户和物品特征矩阵的维度K、物品标签属性数据T1、物品标签关联度矩阵T2、物品流行度矩阵P、算法最大迭代次数maxepoch、正则化系数λ、物品相似度调和系数β、用户偏好相似度的正则化系数λW、物品相似度的正则化系数λS、学习速率α，读入总批次num_batches及每批读取数据的数量batch_size.

输出：用户潜在特征矩阵UMK和物品潜在特征矩阵VNK，迭代次数变化时RMSE的变化情况.

具体步骤如下：

Step 1.读入用户物品评分矩阵，并按8：2划分数据集为实验用到的训练集和测试集；

Step 2.利用用户评分数据及物品标签属性数据计算用户之间的偏好相似度，得到用户相似度矩阵W；

Step 3.根据物品标签关联度矩阵和物品流行度矩阵计算物品之间的相似度值，进而得到物品的相似度矩阵S；

Step 4.初始化用户特征矩阵和物品特征矩阵为正态分布；

Step 5.分批读入训练集中的数据，根据公式(18)计算目标函数；

Step 6.根据公式(21)和公式(22)迭代计算用户特征和物品特征，并计算训练集和测试集的RMSE.

5 实验分析

本文的研究主要有两个目的：

1)验证UPIS-PMF算法优于传统推荐算法；

2)验证从物品角度考虑也可以提高概率矩阵分解的评分预测准确性.

5.1 数据集

本文算法所用数据集为Movielens-100k数据集和Tag-genome数据集，这两个数据集都属于Movielens数据集，其中Movielens-100k数据集包含用户物品评分数据，物品标签属性数据等，Tag-genome数据集包含物品标签属性数据，物品标签关联度数据和物品流行度数据等，后者数据集可以对前者进行补充，两者组合即为最终要使用的数据集[14].组合数据集包含信息有943名用户对1682部电影的评分数据、1682部电影的属性数据、1547578条电影标签关联度数据、1372部电影的流行度数据.

第三，帮助宗教界在经济上实现自养。领导宗教界独立自主自办宗教，实现自治、自传，其中很重要的一点就是培养宗教界能够不依赖于西方帝国主义的津贴，在经济上实现自力更生，自我发展。

5.2 评价指标

为了验证本文算法的相对优劣，本文采用均方根误差RMSE(Root Mean Square Error)作为评价指标，RMSE计算方法如公式(23)所示：

(23)

公式(23)中，Γ为测试集，采用均方根误差作为评价指标对算法结果要求更为严格，更能对比出算法的相对优劣.

5.3 参数调整

本文提出了UPIS-PMF算法，该算法包含的参数有用户特征矩阵和物品特征矩阵的维度K、迭代次数maxepoch、正则化系数λ、物品相似度调和系数β、用户相似度的正则化系数λW、物品相似度的正则化系数λS、学习速率α，读入总批次num_batches及每批读取数据总量batch_size.

对于参数K，通常取值很小时就可以取得较好的实验结果，在本文的实验中，选取参数范围为[2,10]，并对比在不同迭代次数下测试集RMSE的变化情况，实验结果如图2所示.

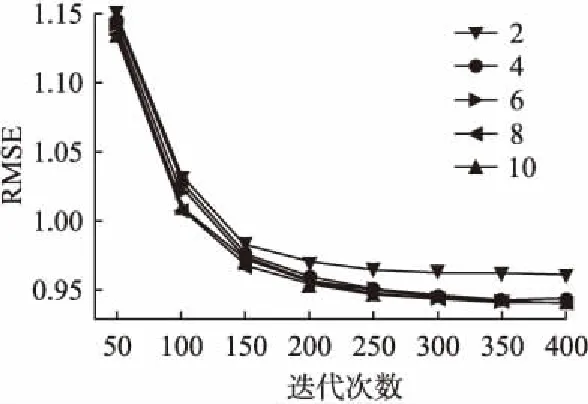
图2 不同参数K及迭代次数对实验结果的影响Fig.2 Effect of different parameter K and iterations on experimental results

由图2可以发现，当参数K取值为2时，算法的结果整体较差，同时，取值为4到10时，算法结果较为接近，因此，合适的参数K应当取值为10.

参数β用以调整物品标签相似度及物品流行度乘积对物品综合相似度的影响程度，取值接近于1，在本文的实验中，选取0.6、0.7、0.8、0.9、1.0五组数据进行实验对比，实验所得结果如图3所示.

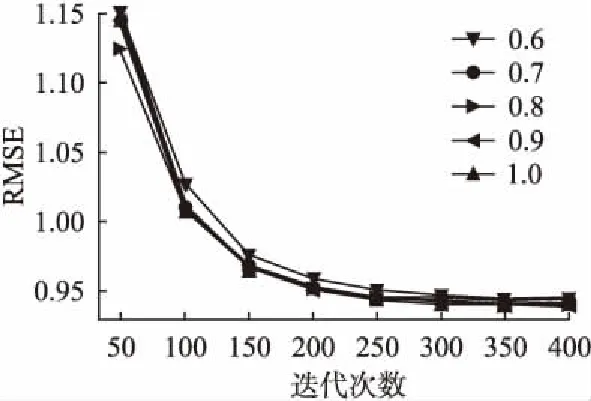
图3 不同参数β及迭代次数对实验结果的影响Fig.3 Effect of different parameter β and iterations onexperimental results

正则化系数用以调整算法性能，防止出现过拟合，结合广大专家学者的已有实验，在本文的实验中，将选取0.001、0.005、0.01，0.05和0.1五组数据进行实验对比，结果如图4所示.

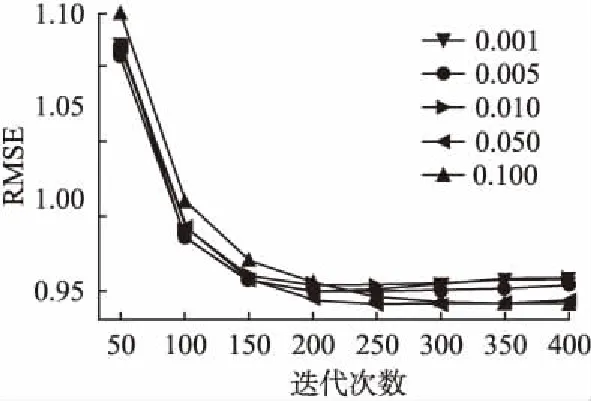
图4 不同参数λ及迭代次数对实验结果的影响Fig.4 Effect of different parameter λ and iterations onexperimental results

由图4可知，UPIS-PMF算法在迭代次数增加时，不同的参数λ均会使算法结果逐渐变优并趋于稳定，当参数值小于0.05时，迭代次数小于200，算法结果较好，但是迭代次数大于200时，参数取值为0.05或0.较好，所以，在本文的算法中取该参数值为0.1.同时，λW与λS对实验的影响与λ类似，为了不失一般性，λW与λS取值也均为0.1.最后，对于学习速率α，该参数不影响实际的算法结果，只影响算法迭代取值的快慢，因此，为了便于对比算法性能，在本文的实验中将取值为1.

5.4 算法对比

经过一系列的实验，UPIS-PMF算法中的参数得到了调整，为了验证对比本文算法的相对优劣，将选取其他几种推荐算法进行对比分析.由于UPIS-PMF属于矩阵分解算法，而且算法的结果与迭代次数有关，因此，将选择同样与迭代次数有关的几种算法，进行对比的算法有FunkSVD矩阵分解推荐算法、概率矩阵分解推荐算法(PMF)、基于用户偏好相似度的概率矩阵分解推荐算法(UP-PMF)和基于物品相似度的概率矩阵分解推荐算法(IS-PMF).实验所得算法对比结果如图5所示.

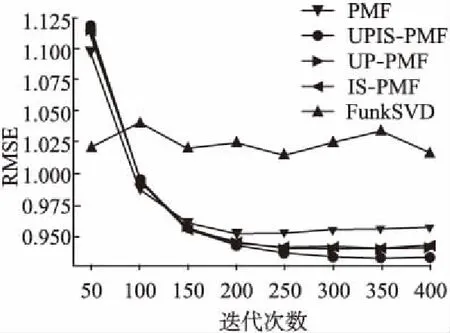
图5 不同迭代次数下的各类算法对比图Fig.5 Comparison of various algorithms underdifferent iteration times

图5展示了UPIS-PMF、UP-PMF、IS-PMF，PMF和FunkSVD五种算法在迭代次数变化时的RMSE变化情况.随着迭代次数的增大，FunkSVD算法整体结果变化较小，而其它四种算法的RMSE值先变小后趋于平缓.当迭代次数小于70时，FunkSVD算法预测准确性优于其它四种推荐算法，当迭代次数大于70时，其它四种算法的预测效果较好，且对于这种四种算法来说，PMF算法的整体结果最差，UPIS-PMF算法和IS-PMF算法整体结果较为接近，且优于PMF算法，一定程度上说明了在概率矩阵分解模型中融入用户相似度或者物品相似度均可以提高预测准确性.最后，对于本文的推荐算法，即UPIS-PMF，算法的预测准确性整体最高.

6 总结和展望

概率矩阵分解推荐算法在评分预测准确性方面优于传统的推荐算法，且广大专家学者从用户角度出发，将用户之间的关系融入概率矩阵分解模型中，组合后的算法提高了评分预测准确性.本文在前人的基础上提出了融合用户偏好和物品相似度的概率矩阵分解推荐算法，通过用户偏好寻找用户之间的相似度关系，利用物品标签关联度数据和物品流行度数据计算物品相似度，将用户相似度矩阵和物品相似度矩阵共同融入概率矩阵分解模型中，Movielens数据集中的实验表明该算法优于传统的推荐算法，同时也说明了从物品角度进行考虑也可以提高评分预测准确性.

最后，在本文算法的计算过程中，由于数据集信息有限，仅通过用户偏好数据计算用户相似度，物品标签关联度数据及物品流行度数据计算物品相似度，计划寻找用户物品信息更多的数据集，利用更多的信息计算对应的相似度，从而使得算法的预测准确性得到更近一步的提升.