一条物理公式的数学变形引发学习进阶

江宁

摘 要：“学习进阶”更注重每一个“阶”度学生在学习“同一内容”时的不同思考方式.本文以“杠杆原理”为例，研讨学生在不同的“阶”度对于此主题产生的不同认知.在“阶”度中通过思考方式的提升，可以促进学生对主题的深度学习，从而使研究更加有利地发展.

关键词：学习进阶，物理公式，杠杆原理，公式变形，简单机械

文章编号：1008-4134（2020）08-0034    中图分类号：G633.7    文献标识码：B

1 关于“学习进阶”在教学中的定义

学习进阶（learning progressions，简称LPs）也称学习进程，是近几年在美国科学教育改革中的一个新兴概念，是对学生在各学段中学习同一主题的概念时所遵循的连贯而典型的学习路径的描述，一般呈现为围绕核心概念而展开的一系列由简单到复杂、相互关联的概念序列[1].

学习进阶包括内容进阶和思维进阶.要构建学习进阶，首先要明确什么是学习中的“阶”，这个“阶”并不只是學习者认知发展的路径，更不只是学习内容的提高，它更代表了学生不同的思考方式，换句话讲，在更高层级的“阶”上的学生并不是比更低层级“阶”上的学生“知道的更多”，而是他们对内容的理解方式方面存在着差异[2].学习进阶正是要求教师从学生的角度去理解“进阶”对于学生进一步学习和发展的意义.

关注学生的进阶，最重要的是关注学生的思考，关注学生在不同阶段对所学的同一内容产生的不同思考方式.由于思维方式的提升，学生可以很方便地进行内容进阶.下面以初中物理“简单机械”中的杠杆原理为核心，来谈谈如何达成学习进阶.

2 思维导图带来的缺失

如图1所示是初中物理“简单机械”一章的概念思维导图，它把简单机械中的关键词与图像、颜色等建立记忆链接，虽然图文并茂，但在学生看来，简单机械的各知识点还是独立的，对于知识点的掌握必须要通过机械的阅读和记忆.  从图1看来，对于知识点的学习过于强调“图像记忆”和“发散联想”，对于抽象思维能力弱的学生，“图像记忆”可以帮助他们提高记忆的效率，但无法加深对知识的理解，因此借助思维导图属于一种肤浅的机械学习.因为物理知识都是有其内在逻辑结构的，由不得胡思乱想，而无序列的“发散联想”具有天马行空、思维难控的特点，所以不适用于物理知识的学习.真正的物理知识的学习，应该注重“理解性记忆”和“条理性思考”，学习的过程中强调的是“理解的深度”而非“记忆的速度”.

3 在思维的循序渐进中促成进阶

根据学生已掌握的概念和认识层次，学习进阶以核心知识点为突破口，建立从简单到复杂的知识序列，逐渐提高学生的思维阶梯，逐一实现从小目标到大目标的过渡，即遵循教育心理学中的循序渐进原则，帮助学生逐级构建物理概念，促进学生思维的逐级提高，从而使学生的科学素养得以逐级的提升.

3.1 建构杠杆模型

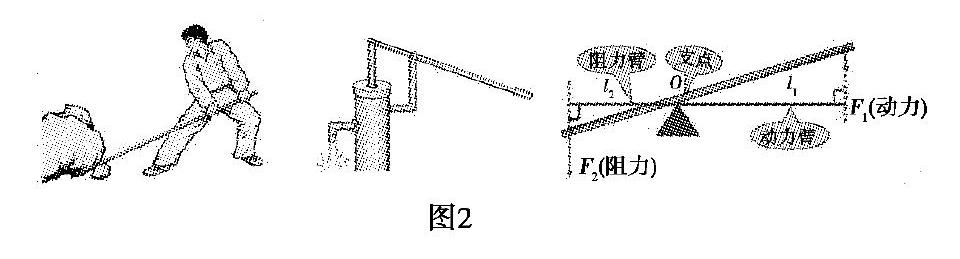
学会建构模型是学习物理的良好开端.如图2所示，在初中物理“简单机械”一章中，通过对典型事例的分析，构建出“杠杆”模型，并定义出杠杆的“五要素”.“杠杆”模型是一种很普通的结构模型，在日常生活中运用非常广泛，教师在教学过程中通过师生列举实例的方式来加强学生对“杠杆”模型的认识，并及时纠正学生对“硬棒”的片面认识，让学生清楚：杠杆的本质是“绕点旋转”.此时，学生的思维建立在如何操作物理模型上，并开始认识虚拟物理量——力臂.

3.2 归纳杠杆原理

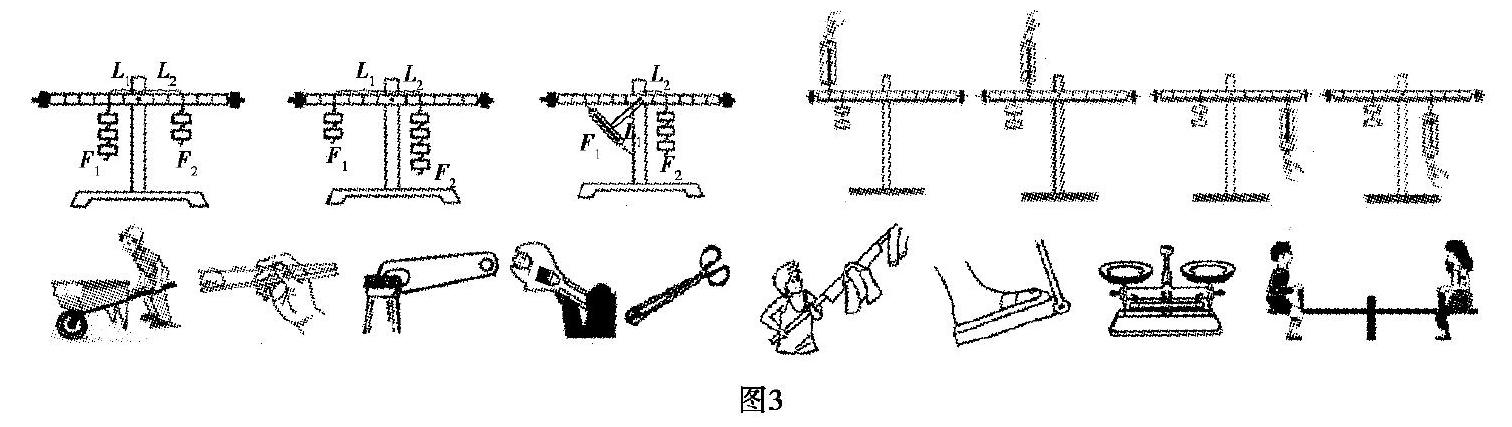
会分析实验数据是研究物理的一种能力.如图3所示，师生通过实验，可归纳出杠杆原理：动力×动力臂=阻力×阻力臂，用数学式表示为F1·L1=F2·L2.式中F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂.从公式可看出，要使杠杆达到平衡，动力臂是阻力臂的几倍，阻力就是动力的几倍.在此基础上定义出三类杠杆：省力杠杆、费力杠杆和等臂杠杆.此时，学生的思维建立在物理模型的计算上，开始向物理模型的实际分类上转变.

3.3 拓展杠杆原理

拓展物理概念是应用物理原理的实际操作.如图4所示，在掌握“绕点旋转”和“变形硬棒”的基础上，推出“定滑轮”和“动滑轮”的定义，即：定滑轮是省力杠杆，动滑轮是动力臂为阻力臂两倍的杠杆，同时可以用“杠杆原理”公式进行计算.根据分析，滑轮的省、费力情况以及省、费距离情况变得清晰可见.以此为契机，轮轴的工作原理也就迎刃而解.  此时，学生的思维建立在物理模型的简单运用上，并有有序发散思维的欲望.如果所有的教学至此就戛然而止，学生对“杠杆原理”的认识就只能局限于受力少的简单机械，思维也只能围绕简单模型展开分析，最终能提高的只是学生的数学计算能力.

3.4 变形物理公式

在杠杆原理公式F1·L1=F2·L2中，如果杠杆受力较多，可按力和力臂乘积的作用效果进行等效合成，得：FALA+FBLB+FCLC=FDLD+FELE+FFLF，即所有使杠杆顺时针转动的力的大小与其对应力臂的乘积之和等于所有使杠杆逆时针转动的力的大小与其对应力臂的乘积的和.如图5所示，杠杆平衡时也就可以运用公式F1L1+F5L5=F2L2+F3L3+F4L4来解题了.此处公式的演绎是学生学习进阶的关键，思维也因此得到拓展，学生对公式的理解并不是靠教师的简单提供，而是学生自身思维不断提升的必然结果.

3.5 提升物理思维

学习进阶的关键是思维升级，在于从更高的思维角度来思考原来的初始问题，从而在达成学习内容进阶的同时，悟出物理原理的本质.

就简单机械而言，现实生活中的杠杆不可能只像理想模型那样受简单的两个力，通过学习的进阶，对于较复杂的机械，也不难让学生分析出其中的物理原理.

如圖6所示为生活中最常见的杆秤，杆秤重心在B点，提纽作为支点在O点，重物通过秤钩作用在A点，秤砣作用在C点，可得：G砣×CO=G秤×BO+G物×AO.

学习进阶后，可以分析如图7所示的差动滑轮的工作原理，这也是杠杆受多力平衡的应用：设物体重力为G，人对链条的拉力为F，轮轴的轮半径与轴半径分别是R和r，绕过动滑轮的两段链条对轮轴的拉力大小都为F′=G2，当多力作用在杠杆上时，可根据公式：F动L动+F′动L′动=F阻L阻，那么FR+F′r= F′R，从而得出F=R-r2RG[3].

围绕杠杆原理，由于公式的变形，学习的内容在此基础上顺利进阶，学生在不同的“阶”度上都有了自己不同的思考方式，“阶”度的提高促成了学生思维层级的发展.

4 在学习的时间与空间的融合中达成学习进阶

学习进阶更加关注的是学生如何思考.从时间上来说，学习进阶一般需要经历一段学生成长历程的研究，在研究过程中，思维结构伴随着逐级升级的“阶”度趋向完善，从空间上来说，正因为“阶”度的提升，学生认识物理世界的起点逐级提高，“前概念”“错误思维”得以及时纠正，对某个知识点的认识从低水平、想当然转变为高认知、所以然.学习时间与学习空间的有效融合将学习的起点和终点连接起来，更有利于学生形成清晰而有条理的思路，不同层次的学生在不同的“阶”度上思维都能有所提高.

支持碎片理论认为：学生的知识来源于一些零散的知识碎片，面对新的物理情境，学生需要将这些碎片知识重组并构.但机械式的知识重构只会诱发学生进行机械记忆，认知思维在此过程中仍然是零散孤立的.而学习进阶是以知识点为核心，把握学生认知中的关键问题，通过逐级思考形成系列的学习轨迹，从而促进学生的认知构建，促使学生对核心概念的认识在较长时间内不断深化.

由于学生认知规律存在个体差异，不同学生对某一核心知识的学习进阶路径可能是不同的[4]，因此，学习进阶要基于学生的生活经验，关注学生的认知发展，为学生的学习设计出一种行之有效和相对理想的路径以达成学习目标，围绕知识点在时间维度上的研讨、在空间维度上的积累，最终促成学生思维能力的提升[5].

参考文献：

[1]刘晟，刘恩山.学习进阶：关注学生认知发展和生活经验[J].教育学报，2012，8（02）：81-87.

[2]ALICIA C.ALONZO，翟小铭.学习进阶：描述学生思维发展的有效方式[J].物理教师，2015，36（11）：73-76.

[3]张巍继. 基于学习进阶理论下西藏小学科学与初中物理衔接问题研究[D].西藏：西藏大学，2019.

[4]李光宇.基于“学习进阶”理论的物理习题教学策略[J].教学月刊·中学版（教学参考），2016（Z2）：31-35.

[5]杨凯. 基于学习进阶的初中物理光学部分微课资源构建[D].江苏：苏州大学，2018.

（收稿日期：2020-01-13）