直观想象的三个层次
2020-04-10李琳
中学课程辅导·高考版 2020年4期
李琳


直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的过程.主要包括:借助空间认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系;构建数学问题的直观模型,探索解决问题的思路.
直观想象是发现和提出数学问题、分析和解决数学问题的重要手段,是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础.在直观想象核心素养的形成过程中,同学们能够进一步发展几何直观和空间想象能力,增强运用图形和空间想象思考问题的意识,提升数形结合的能力,感悟事物的本质,培养创新思维.
层次一、直面感官想象的能力
能够在熟悉的情境中,建立实物的几何图形;能够建立简单图形与实物之间的联系,体会图形与图形、图形与数量的关系.
能够在熟悉的数学情境中,借助图形的性质和变换(平移、对称、旋转)发现数学规律;能够描述简单图形的位置关系和度量关系及其特有性质.
能够通过图形直观认识数学问题;能够用图形描述和表达熟悉的数学问题、启迪解决这些问题的思路,体会数形结合.
能够在日常生活中利用图形直观进行交流.
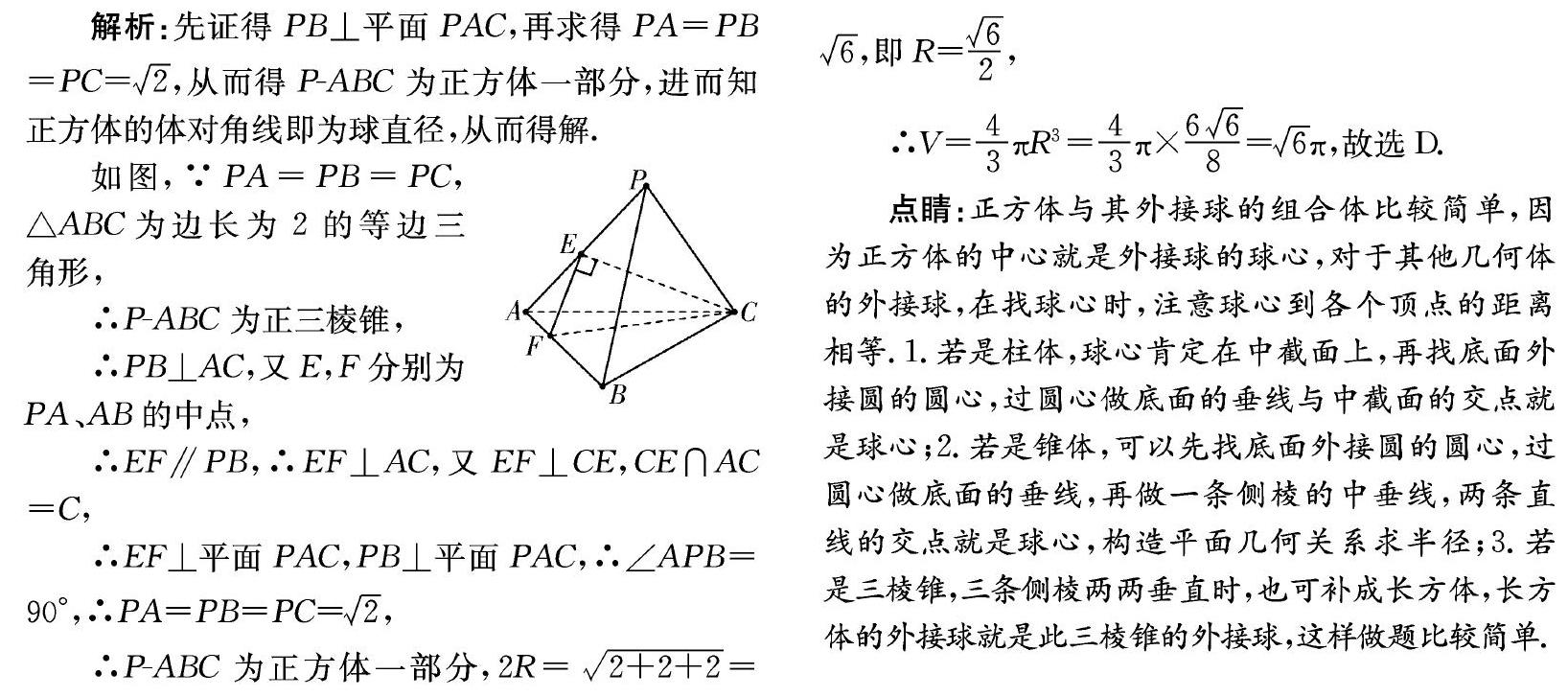
点睛:正方体与其外接球的组合体比较简单,因为正方体的中心就是外接球的球心,对于其他几何体的外接球,在找球心时,注意球心到各個顶点的距离相等.1.若是柱体,球心肯定在中截面上,再找底面外接圆的圆心,过圆心做底面的垂线与中截面的交点就是球心;2.若是锥体,可以先找底面外接圆的圆心,过圆心做底面的垂线,再做一条侧棱的中垂线,两条直线的交点就是球心,构造平面几何关系求半径;3.若是三棱锥,三条侧棱两两垂直时,也可补成长方体,长方体的外接球就是此三棱锥的外接球,这样做题比较简单.
