织物褶皱多尺度灰度共生矩阵分析
2020-04-10石康君王静安高卫东
石康君 王静安 高卫东

摘要: 为建立一套客观、稳定、高效的织物褶皱评价系统,文章提出一种多尺度图像特征提取方法。首先,通过3层小波变换对织物二维图像进行分解,得到其高频系数;对原图及三个尺度下的小波系数分别生成灰度共生矩阵,并对这四个尺度的灰度共生矩阵提取对比度、相关性、角二阶矩、同质性及熵值表征织物褶皱变化;最后通过支持向量机对输入特征进行分类。结果表明,结合小波变换的灰度共生矩阵方法比单独使用灰度共生矩阵分类准确率高,说明多尺度的图像特征能够更加全面地描述织物褶皱变化。
关键词: 织物褶皱;小波变换;灰度共生矩阵;多尺度;支持向量机
中图分类号: TS941.2文献标志码: A文章编号: 10017003(2020)02003506
引用页码: 021107DOI: 10.3969/j.issn.10017003.2020.02.007
Multiscale GLCM analysis of fabric wrinkles
SHI Kangjun, WANG Jingan, GAO Weidong
(Key Laboratory of EcoTextiles, Ministry of Education, Jiangnan University, Wuxi 214122, China)
Abstract: In order to establish an objective, stable and efficient evaluation system of fabric wrinkles, this paper proposes a multiscale image feature extraction method. Firstly, the 2D images of fabrics were decomposed by threelayer wavelet transform to obtain the highfrequency coefficients. The GLCM(graylevel cooccurrence matrix) was respectively generated for the original images and the wavelet coefficients at three scales, and the contrast, correlation, angular secondary moment, homogeneity and entropy of the GLCM of the four scales were extracted to characterize the fabric wrinkle change. Finally, SVM(support vector machine) was applied to classify inputted features. The results show that the GLCM method combined with wavelet transform has higher classification accuracy than the GLCM method alone, indicating that multiscale image features can more comprehensively describe fabric wrinkle changes.
Key words: fabric wrinkle; wavelet transform; GLCM; multiscale; SVM
在紡织与服装行业,织物洗后外观褶皱等级作为评价织物外观性能与抗皱性能的重要指标,其评价方法一直是行业研究的难点。目前,AATCC评价方法是被应用最广的一种方法。但此方法是一种主观评价方法,评价结果依赖于观测者对褶皱的主观感知,没有统一的标准,个体之间的评价结果可能出现较大差异,且人工评价耗时、费力、效率低下,不符合纺织智能制造的发展趋势。
随着计算机技术的发展,许多研究者将计算机视觉应用到织物褶皱评价的研究中。20世纪90年代,XU B等[1]使用扫描仪获取织物表面图像,基于像素信息定义了表面比和阴影比两个变量,以量化表征织物褶皱表面。MORI T等[2]利用二维图像灰度值及其位置信息生成灰度共生矩阵,从中提取特征值量化褶皱,并利用神经网络对特征向量进行训练,取得了较高的分类结果。相比于时域分析,频域分析有着更加显著的优点。CHOI C J等[3]利用2D傅里叶变换,将时域信号转换到频率域,提取局部频率范围的频谱幅值表征织物褶皱程度。
由于使用二维图像的褶皱评价方法是基于图像灰度值及其位置信息进行表征,评价结果易受图像采集环境及织物表面颜色影响。因此,三维图像被应用到织物褶皱评价的研究中。KANG T J等[46]在基于三维图像的织物褶皱客观评价中做了大量工作,他们分别使用激光扫描与立体视觉技术获取了较为精确的AATCC模板表面图像。YANG X B等[78]提出了一种基于光度立体视觉的织物三维外观重建方法。但是获取织物三维图像用时过长,不能达到快速检测的目的,且成本较高,限制了其在工业上的应用。
本文将小波变换与灰度共生矩阵结合对织物二维图像进行分析,在多个尺度提取褶皱特征表征织物褶皱等级。结果表明,相比单一尺度的图像特征,多尺度灰度共生矩阵特征能够更加全面地描述织物褶皱变化。
1图像采集系统
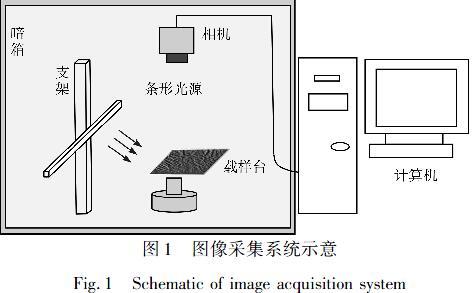
本文在单侧光环境下采集标准模板与织物样本图像。织物图像采集系统主要包括条形光源、CCD相机、暗箱、支架、载样台。图1为图像采集系统示意。
如图1所示,条形光源位于载样台一侧,并与载样台一边平行。由于光源垂直位置高于待测样本,其产生的光线与待测样本形成一定的入射高度角,当光线照射到粗糙样本表面后,经漫反射于不平整的样本表面产生不同的反射光线,表现在图像中则为区域性的明暗变化。且SA1模板表面最粗糙,漫反射更强烈,明暗变化也更加明显。随着褶皱等级的提高,明暗变化逐渐减弱。采集所得六个等级AATCC标准模板图像,如图2所示。
织物褶皱多尺度灰度共生矩阵分析2基于快速小波变换的多尺度图像分析
当对数字图像进行多分辨率分析和处理时,小波变换是一种重要的数学工具,它能够有效、直观地描述图像纹理特征。
2.1小波变换原理
小波变换是在傅里叶变换的基础上发展起来的一种信号的时频分析方法,具有多分辨率分析的特点。二维小波变换是通过高通hθ和低通hφ滤波器与原始信号卷积,把输入信号分解为四个低尺度分量。对于二维信号f(x,y)一次完整的分解过程如图3所示。
f(x,y)hθ(-n)2↓hθ(-m)2↓wDθ(j,m,n)hφ(-m)2↓wVθ(j,m,n)hφ(-n)2↓hθ(-m)2↓wHθ(j,m,n)hφ(-m)2↓wHφ(j,m,n)
图3中,变量j、m、n分别为尺度、水平位移和垂直位移;wφ(j,m,n)为低频系数(近似系数),{wDθ(j,m,n)=H,V,D}分别为水平、垂直和对角线高频系数(细节系数);2↓表示2倍下取样。图3为第一层分解过程,第二层分解则将wφ(j,m,n)作为输入信号执行上述过程。
2.2图像多尺度分析
一副褶皱的织物图像经多层小波变换后,每层信息都被分解为高频分量H(褶皱边缘和噪声)和低频分量L(图像的主体)两部分[9]。高频分量又被分解为水平高频分量HH、垂直高频分量HV和对角线高频分量HD。经过小波变换分解得到的低频分量包含原图像90%以上能量,低频失去的信息由高频捕获[10],继续进入下一层分解。每一层分解仅对低频分量进行。图4(a)是对图像进行三层小波分解的示意,图4(b)为一副褶皱织物图像三层分解结果。图4小波分解示意
Fig.4Schematic of wavelet decomposition由图4可知,每经过一层小波变换后,图像都被分解为4个1/4大小的新图像,即由上级图像与小波基进行内积后,再分别沿图像行和列方向进行2倍间隔抽样而成。因此,可以通过对图像进行多层小波变换,在不同尺度下对织物褶皱特征进行分析。需要注意,图像尺寸随分解层数的增大呈指数减小,分解层数不易过高。由于低频分量包含原图像90%以上能量,与原图非常相似,而高频分量含有的信息较少,且每一层的高频分量都较好地保留了织物的边缘特征,因此本文采用原图和3层小波变换分解所得高频分量进行褶皱特征提取。且通过实验证明,选用haar小波时,灰度共生矩阵特征能够更好地描述褶皱等级变化。
3基于灰度共生矩阵的褶皱特征提取
灰度共生矩阵是描述图像灰度分布及像素相对位置关系的一种图像分析方法,可以反映图像在方向、像素间隔、变化幅度及快慢的综合信息[11]。
3.1图像多尺度灰度共生矩阵求取
由于褶皱是一种纹理信息,灰度共生矩阵是一种常用的分析纹理特征的方法,因此很多研究者將灰度共生矩阵用于织物褶皱的客观评价[2,12]。在早期研究中,研究人员都是在单一尺度下对图像生成灰度共生矩阵,提取褶皱特征。但纹理本身的层次性使其在不同的尺度下呈现出不同特征,单一尺度下的图像特征不能完全反映出纹理的本质特性,因此本文在4个尺度下生成灰度共生矩阵,即原图及三层小波变换分解所得高频小波系数。
灰度共生矩阵是图像的一种二阶统计量。给定一副数字图像I(x,y),其灰度级为L,则灰度共生矩阵G(x,y)为I(x,y)中沿方向θ,间隔为d的两个像素点对(i,j)的统计数目n。G(x,y)的尺寸为L×L,n为灰度共生矩阵在G(i,j)的像素值。
对于一副织物图像,经灰度变换后的灰度级L=256,灰度共生矩阵尺寸为256×256。为减少后续计算量,必须将原始图像的灰度级进行压缩,减小G(x,y)的尺寸。通常,将图像灰度压缩至16级,像素间隔d取1是一个合理的选择[11]。由于褶皱在织物中的分布是随机的、无规则的,沿各个方向均匀分布,因此选择θ=0°、45°、90°、135°四个方向分别生成灰度共生矩阵,提取特征表征织物褶皱等级。
3.2AATCC标准模板褶皱特征提取
由于在织物褶皱客观评价研究中,没有标准的织物数据库用于参考,而AATCC标准模板是被行业普遍认可和信任的参照样本,因此对AATCC标准模板图像按照上述步骤生成灰度共生矩阵,并从中提取描述纹理的特征值。对于一副灰度级为L的图像,典型的纹理特征有以下几种:
1)对比度。
对比度反映了图像的清晰程度和褶皱的变化幅度。对于一副织物图像,表面越皱,对比度越高。
F1=∑Li=1∑Lj=1(i,j)2pij(1)
式中:Pij为灰度共生矩阵在点G(i,j)的概率统计。
2)相关性。
相关性为返回某个像素与其相邻像素间关系的度量,表示图像中纹理的非均匀程度和复杂程度。
F2=∑Li=1∑Lj=1(i-mr)(i-mc)pijσrσc(2)
式中:mr和mc分别为沿灰度共生矩阵G的行和列计算所得均值,σr和σc为行和列标准差。
3)角二阶矩。
角二阶矩是图像灰度分布均匀程度的度量。其值越大,表明织物表面变化缓慢,织物越平整。
F3=∑Li=1∑Lj=1pij(3)
4)同质性。
同质性用于度量灰度共生矩阵元素关于主对角线的集中程度。一副图像的灰度级越丰富,变化越缓慢,其同质值越高。
F4=∑Li=1∑Lj=1pij1+|i-j|(4)
5)熵。
熵值是图像中所具有的信息量的度量,代表了图像的复杂程度,是图像内容随机性的度量。
F5=-∑Li=1∑Lj=1pijlogpij2(5)
一副图像经小波变换分解后每层可以得到3副子图像,分别对应高频水平系数(wHθ)、高频垂直系数(wVθ)和高频对角线系数(wDθ)。经3层小波变换分解后可得到9副子图像。首先对AATCC标准模板原图及其9副子图像在θ=0°、45°、90°、135°四个方向提取的特征求均值,然后再分别对每一层高频系数wHθ、wVθ和wDθ所得特征求均值作为当前尺度的特征值,并将4个尺度的特征值组合,由此每一样本可得到一个20维的特征向量。表1列出了AATCC标准模板原图及小波变换分解所得2个尺度的小波系数特征提取结果。
3.3织物褶皱特征提取
由于AATCC标准模板是塑料制品,表面周期性纹理信息弱,而织物是经纬纱按照一定规律交织组成,具有较强的周期性。因此,通过AATCC模板确定的灰度共生矩阵特征在真实织物上的有效性是一个值得讨论的问题。为验证上述特征在真实织物上的有效性,对6个等级的345块织物图像根据上述步骤提取褶皱特征,并绘制箱型分布图。图5随机展示了部分特征值统计结果。由图5可知,在不同尺度下,织物特征值随等级变化具有一定的分布梯度。
4基于支持向量機的褶皱评价
20世纪90年代,Vapnik提出的统计学习理论[1314]在模式识别领域得到广泛应用,支持向量机在此理论基础上采用结构风险最小化准则设计机器学习模型,较好地解决了小样本、非线性、高维数的分类问题。
4.1支持向量机模型优化
使用支持向量机对织物褶皱等级进行分类预测时,主要考虑原始数据的缩放比例,核函数的类型选择,惩罚参数c,核函数宽度g的选取。由于经典支持向量机是为了解决2分类问题设计的,而织物褶皱等级评定是一个6分类问题,因此本文采用Libsvm[15]软件包来解决织物褶皱的分类问题。
由表1可知,图像在不同尺度下的特征差值很大,为避免较大范围内的数值属性影响较小范围内的数值属性,在分类前,将特征值归一化。Libsvm软件包常用的核函数有4种,分别是线性核、多项式核、RBF核及Sigmoid核。为保证取得最好的分类结果,分别选择上述4种核函数对织物样本进行训练和测试,通过比较分类结果选择合适的核函数。为了更好地提高支持向量机性能,需调节相关参数。对于多项式核、RBF核及Sigmoid核,主要调节惩罚参数c和核函数参数g,对于线性核函数主要调节参数c。通常最佳(c,g)值的选择通过交叉验证和网格搜索来确定。在交叉验证前,粗略确定(c,g)值的搜索范围,并根据网格搜索等高线图调整其范围。本文采用五折交叉验证寻找最佳(c,g),首先将训练集平均分成5组,得到5组子集,每个子集分别做一次验证集,其余4组子集作为训练集,由此得到5个模型。按这5个模型验证集的平均分类准确率作为最终交叉验证的准确率,使用交叉验证准确率最高的(c,g)组合优化支持向量机。
4.2褶皱等级评价
为验证多尺度灰度共生矩阵特征及支持向量机在织物褶皱等级评价中的应用效果,对345块(65%作为训练样本、35%作为测试样本)已知褶皱等级的白色织物样本进行特征提取,并使用支持向量机进行分类预测。采用网格搜索寻找最佳(c,g),以RBF核函数的参数优化为例,搜索结果如图6所示。
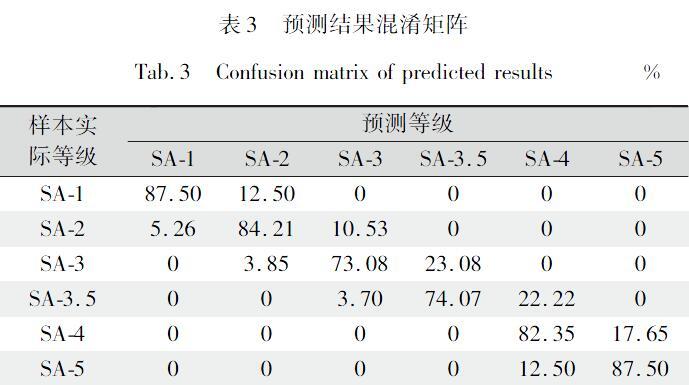
由图6可知,当(c,g)=(2 724.077)时,交叉验证的准确率最高。以此(c,g)值组合优化支持向量机模型,对测试样本进行分类预测。并分别使用线性核、多项式核、Sigmoid核重复上述参数寻优过程,不同核函数支持向量机分类结果如表2所示。由表2可知,核函数类型对最终分类结果影响较大,在本文使用算法中,当核函数类型为RBF核时支持向量机分类结果最好,测试样本准确率可达80.17%。
表3展示了采用RBF核的支持向量机分类结果。由表3可知,错分类样本主要集中在SA3和SA3.5之间,这主要由两种不同褶皱类型的外观差异造成的。由图2可知,SA3的褶皱锐利且密度高,而SA3.5的褶皱具有更大的尺寸和更加平缓的变化,这为褶皱评价带来了一定困难。
4.3分类方法对比
为验证本文提出的方法在织物褶皱客观评价中的优越性,基于相同的样本集将本方法的执行结果与文献[1618]使用方法及单一尺度的灰度共生矩阵方法进行对比,结果如表4所示。由表4可知,本文提出的方法分类准确率显著高于其他方法,说明多尺度的图像特征能够更加全面地描述织物褶皱变化。
5结论
针对单一尺度灰度共生矩阵方法描述织物褶皱特征的不足,本文通过小波变换对图像进行分解,得到多个尺度下的图像,并在不同尺度下对高频小波系数进行灰度共生矩阵分析,提取特征值,比较全面地描述了褶皱特征随织物等级的变化。通过优化的支持向量机模型对345块织物样本进行分类预测,证明了本方法在织物褶皱客观评价中的应用价值。
由于单测光采集环境的限制,本文采用方法并不适用于多色织物的褶皱评价,且SA3与SA3.5之间的外观差异为织物褶皱评价带来了一定困难,因此在接下来的研究中将对上述问题进行深入分析。
参考文献:
[1]XU B, REED J A. Instrumental evaluation of fabric wrinkle recovery [J]. Journal of the Textile Institute, 1995, 86(1): 129135.
[2]MORI T, KOMIYAMA J. Evaluating wrinkled fabrics with image analysis and neural networks [J]. Textile Research Journal, 2002, 72(5): 417422.
[3]CHOI C J, KIM H J, JIN Y C, et al. Objective wrinkle evaluation system of fabrics based on 2D FFT [J]. Fibers and Polymers, 2009, 10(2): 260265.
[4]KANG T J, CHO D H, KIM S M. New objective evaluation of fabric smoothness appearance [J]. Textile Research Journal, 2001, 71(5): 446453.
[5]KANG T J, LEE J Y. Objective evaluation of fabric wrinkles and seam puckers using fractal geometry [J]. Textile Research Journal, 2000, 70(6): 469475.
[6]KANG T J, KIM S C, SUL I H, et al. Fabric surface roughness evaluation using waveletfractal method(part I): wrinkle, smoothness and seam pucker [J]. Textile Research Journal, 2005, 75(11): 751760.
[7]YANG X B. A new research of fabric 3D surface shape using photometric stereo [J]. JournalNorthwest Institute of Textile Science and Technology, 2001, 15(1): 2025.
[8]YANG X B, HUANG X B. Evaluating fabric wrinkle degree with a photometric stereo method [J]. Textile Research Journal, 2003, 73(5): 451454.
[9]李艷梅, 仇晓坤, 蒋真真. 缝纫平整度客观评判模型的研究[J]. 丝绸, 2011, 48(4): 2831.
LI Yanmei, QIU Xiaokun, JIANG Zhenzhen. Research on objective evaluating model of seam pucker [J]. Journal of Silk, 2011, 48(4): 2831.
[10]陈燕文. 基于SIFT与小波变换的图像配准融合方法研究[D]. 武汉: 武汉理工大学, 2011.
CHEN Yanwen. Study on Methods of Image Registration Based on SIFT and Image Fusion Based on Wavelet [J]. Wuhan: Wuhan University of Technology, 2011.
[11]高士忠. 基于灰度共生矩阵的织物纹理分析[J]. 计算机工程与设计, 2008, 29(16): 43854388.
GAO Shizhong. Analysis of fabric texture based on GLCM [J]. Computer Engineering and Design, 2008, 29(16): 43854388.
[12]汪黎明, 陈健敏, 王锐, 等. 织物折皱纹理灰度共生矩阵分析[J]. 青岛大学学报(工程技术版), 2003(4): 58.
WANG Liming, CHEN Jianmin, WANG Rui, et al. The analysis of grain of fabric wrinkle by concurrence matrix of gray degree [J]. Journal of QINGDAO University(Engineering & Technology Edition), 2003(4): 58.
[13]VAPNIK V. The Nature of Statistical Learning Theory [M]. New York: Springer Science & Business Media, 2013.
[14]VAPNIK V. An overview of statistical learning theory [J]. IEEE Transactions on Neural Networks, 1999, 10(5): 988999.
[15]CHANG C C, LIN C J. LIBSVM: a library for support vector machines [J]. ACM Transactions on Intelligent Systems and Technology(TIST), 2011, 2(3): 27.
[16]ABRIL H C, VALENCIA E, MILLN M S. Objective assessment of wrinkled fabrics by optical and digital image processing [C]. AIP: AIP Conference Proceedings, 2008, 992(1): 10451050.
[17]ABRIL H C, MILLAN M S, VALENCIA E. Influence of the wrinkle perception with distance in the objective evaluation of fabric smoothness [J]. Journal of Optics A: Pure and Applied Optics, 2008, 10(10): 104030.
[18]SUN J, YAO M, XU B, et al. Fabric wrinkle characterization and classification using modified wavelet coefficients and supportvectormachine classifiers [J]. Textile Research Journal, 2011, 81(9): 902913.
收稿日期: 20190529; 修回日期: 20191210
基金项目: 国家重点研发计划项目(2017YFB0309200);中央高校基本科研业务费专项资金项目(JUSRP51907A);江苏省研究生科研创新项目(KYCX19_1878)
作者简介: 石康君(1993),男,硕士研究生,研究方向为基于图像处理的纺织智能检测。通信作者:高卫东,教授,gaowd3@163.com。
