基于应变监测的升降舵壁板变形重构方法

冯荻，梁冰，刘坤，姜昕彤，贾振元，刘巍

（大连理工大学 机械工程学院，辽宁 大连116024）

0 引言

随着航空航天领域技术的不断发展，应用需求不断提高，新一代的航空航天器需要执行更为复杂多样的任务，其机动性和安全可靠性要求也更高。升降舵作为航空航天器实现功能、提高性能的重要部件，必须确保其在在位装配时的装配精度与结构强度。因此，升降舵壁板结构在装配过程中的实时变形监测对于航空航天器的整体结构稳定与安全有着十分重要的意义。

目前，应用于升降舵壁板几何形状的传感和测量方法主要包括视觉测量方法、激光扫描方法、应变片测量法和三坐标测量方法等［1-4］。这些方法适用于升降舵壁板线下定检时的型面重构，而对于升降舵壁板在线装配时的变形实时监测存在局限性，主要问题集中于在线装配过程中受到各种干扰因素影响以及工装在线工作时存在对升降舵壁板大面积遮挡的情况，从而导致传统测量手段测量速度慢、效率低、稳定性差、相对精度低甚至不能测量，不能应用于升降舵壁板在线装配时的变形实时监测。因此，现有的方法无法应用，需要发展新型的传感与测量技术来解决升降舵壁板在线装配时结构变形的实时监测问题［5-7］。

与传统的应变片等测量方式对比，光纤光栅传感技术有着显著的优势，主要包括：①光纤传感器结构简单、体积小、重量轻、重复性好，较传统传感器更便于布置，且响应时间更短，稳定性更强；②相较于传统测量方式，光纤光栅传感器具有非传导性，对被测介质影响小，又具有抗腐蚀、抗电磁干扰的特点，更加适合于在升降舵装配的复杂工况中使用，可布置在升降舵壁板结构表面，灵敏快速地测量升降舵壁板的变形参数；③轻巧柔软，可以在一根光纤中写入多个光栅，构成传感阵列，与波分复用和时分复用系统相结合，实现升降舵壁板在线装配变形实时监测数据的高速率和大容量的传输［8］；④测量信息采用波长编码，抗干扰能力更强，且具有更高的分辨力，对升降舵壁板变形的高精度重构十分有利。

随着升降舵结构变形监测研究更加深入，光纤光栅形状传感研究更加广泛，基于光纤光栅传感器传递的结构型面应变信息来进行结构变形重构算法的研究逐渐成为该领域的核心研究内容之一。在国外，Davis M.A.等人［9］搭建了应用波分复用技术的光纤光栅传感网络，以悬臂梁结构作为被测目标，利用瑞利-里兹法则对光纤光栅传感得到的应变数据进行优化分析，较为精确地预测了简单悬臂梁的形态；Tessler等人［10］基于应变信息测量结合最小二乘变分方程求解得出被测构件应变场和位移场之间的转换函数，整理出了逆向有限元法；Foss等人［11］根据结构应变振型与位移振型之间存在的对应关系，推导出位移-应变转换矩阵，建立了基于模态转换的结构变形重构算法；Ko等人［12］从梁理论出发，以构件表面的应变信息为基础，提出了Ko位移理论，研究了多种结构的变形监测重构问题。在国内，祝连庆等人［13］以光纤光栅传感技术为基础，研究了基于被测点曲率的曲面重建算法，对变形机翼进行监测与重构；郭蒙等人［14］基于天线阵列单元面板表面的应变信息，推导出天线阵列弯曲的挠度函数，完成了对天线阵列单元的变形监测；王寅等人［15］基于Ko位移理论，对柔性无人机翼梁进行简化，实现了对翼梁变形的监测。

虽然，现有的对航空航天器结构变形的监测与重构方法研究较为丰富，但仅限于单个结构线下强度测试或飞行状态下变形监测，并没有对构件在位装配过程中变形的监测与重构的研究。针对这一问题，本文以光纤布拉格光栅应变传感器为测量手段，采用最小应变误差优化方法对传统变形重构算法进行优化，得到高精度的变形重构算法，对升降舵壁板在线装配时多工况变形监测与重构进行研究，结合有限元仿真分析计算的结果，验证了变形重构算法的精度与稳定性。

1 传感原理及重构算法

1.1 光纤布拉格光栅传感原理

选用光纤布拉格光栅传感器作为应变监测的测量手段。光纤布拉格光栅是在单模光纤的纤芯内对其折射率进行周期性调制形成的传感器件。其基本原理为光纤布拉格光栅的中心波长与纤芯有效折射率、光栅周期之间的关系。基于以上光纤布拉格光栅传感原理结合光纤解调仪对中心波长漂移量的解调，即可实时获取相应测点的应变。

1.2 变形重构算法

飞机升降舵壁板结构变形重构问题，可近似于承受弯曲载荷的梁结构变形，根据欧拉-伯努利经典梁理论，并基于离散的思想，将梁结构作为连续体做离散化处理［12］，在梁长度方向将梁分为一个个微小单元，每个小单元的应变应为线性分布，设梁总长度为l，分为n个单元，每个单元长度为Δl（＝xi-xi-1＝l／n），第i段单元的首节点的长度方向坐标为xi-1，末节点的长度方向坐标为xi，首末节点对应应变分别为εi-1与εi，通过线性插值即得到

对于一个微小单元，也即在xi-1＜x＜xi范围内，单元中的斜率tanθ（x）为

式中：v为横截面上中性轴至梁表面之间的距离。

将式（1）代入式（2）可得到在xi位置的斜率，即为

在xi-1≤x≤xi范围内的位移y（x），由斜率的积分与在xi-1位置的位移两部分组成，即为

将式（1）代入式（4）可得到在xi位置的位移yi，即为

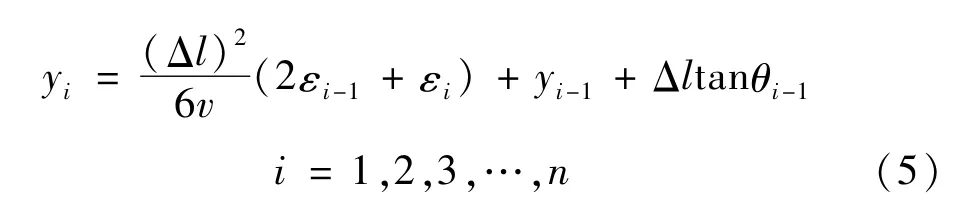
实际工程中，由于构件横截面上中性轴至其表面之间的距离v难以精确测定，因而需要对重构方程（5）进行优化［16］。被测构件在发生变形后，其上下表面对应测点的应变变化几何关系由图1（a）所示，可以等效为图1（b）所示的应变变化几何关系，相应的构件横截面上中性轴至其表面之间的距离v与构件厚度h之间的关系可由上述等效的应变变化几何关系推导得

式中：εt为被测构件上表面测点应变；εb为被测构件下表面测点应变（与上表面测点位置对应）。

图1 构件厚度h与构件中性轴至其表面距离v的关系

将式（6）代入式（3）与式（5）中，即可得到优化后的构件变形重构方程。

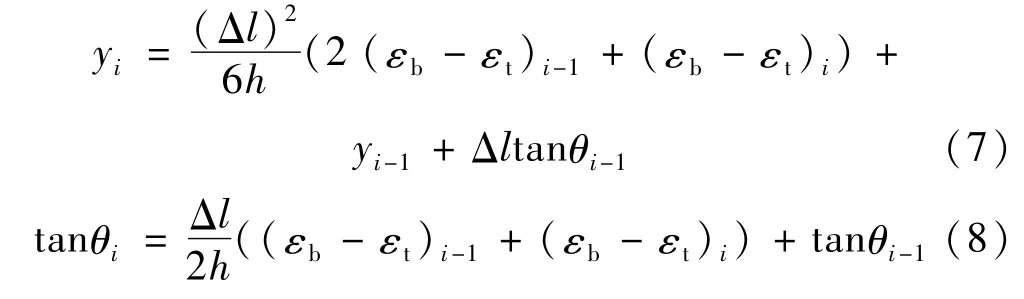
式中：i＝1，2，3，…，n。

对于一端固定、一端自由的构件，边界斜率tanθ0＝0，边界变形位移量y0＝0；对于两端固支的构件，则为y0＝tanθ0＝0，yn＝tanθn＝0；对于一端固定、一端简支的构件，固定端有y0＝tanθ0＝0，简支端则有yn＝0，tanθn≠0。

根据构件不同的固定方式，边界条件已经能够确定，但式中依然存在未知量。将i＝1代入式（7）与式（8）中，除已 知量外，还有 未 知量（εb-εt）0与（εb-εt）1，（εb-εt）1显然可以通过测点的应变传感器测量，然而由于应变传感器本身存在一定体积，实际中难以紧贴构件固定端端部布置传感器，传感器并不能直接测量构件端部测量值（εb-εt）0，现有解决方法是通过其它测点的测量值进行多项式拟合，拟合出构件端部应变（εb-εt）0，但该方法拟合精度差，由于构件的变形重构方程具有误差累积的特点，获得的端部应变（εb-εt）0精度差，直接导致位移重构精度下降。为获取高精度构件端部应变（εb-εt）0，对构件进行有限元仿真分析，得到各个测点的仿真分析应变真值，结合传感器测得的应变测量值，得到最小应变误差优化函数。

式中：ei-1为各个测点应变的误差；（εb-εt）i-1为各个测点仿真分析应变真值；为各个测点的应变测量值；为端部应变优化拟合值。在对最小应变误差优化函数求极小值后，即可求出相应的端部应变优化拟合值，将作为构件端部应变测量值代回式（7）与（8），并根据不同情况，选择不同的边界条件代入式中，即可重构出被测构件形面上多点变形位移值。

2 实验装置与策略

本文针对飞机升降舵壁板结构在位装配过程中的变形问题，展开基于位移重构算法及其优化算法的研究，重构结果与有限元分析结果进行了对比。

实验装置是基于飞机升降舵壁板结构的在线装配变形重构系统，如图2所示。飞机升降舵壁板材料为6061-T6铝，基本尺寸参数如下：长311.32 mm，宽200.01 mm，厚3.12 mm。

图2 飞机结构的在线装配变形重构系统

根据飞机升降舵壁板结构的基本参数及其工作情况，在构件正反两面对称布置了15对光纤光栅应变传感器，传感器间距及具体位置如图3所示。传感器中心波长分布在1510～1590 nm范围内，以5个传感器为一组，串联为一条测量线，两两传感器的中心波长差值均大于5 nm，满足识别要求。以1～5号传感器形成的测量线为例，其中心波长分别为1524.971，1538.762，1555.132，1565.116，1550.051 nm，传感器中心波长的信号图如图4所示。

图3 光纤光栅应变传感器布置图

图4 光纤光栅应变传感器中心波长信号图

实验方法具体流程为：将模拟飞机升降舵壁板的构件按照装配时的固定方式，固定在精密光学平台上，采用多组精度为F1的高精度砝码对构件进行加载，以模拟升降舵壁板在装配过程中的多种工况，将光纤光栅应变传感器分为3大组，串联接入到MOI公司的应变解调仪的6个通道中，解调仪共有16个通道，测量波长范围为1500～1600 nm，误差为1 pm，重复性在1 Hz时为0.05 pm，应变解调仪与电脑服务器连接，并将解调后的应变数据传输到电脑服务器中，电脑服务器利用位移重构算法对数据进行处理，同时根据结构的工作情况进行有限元仿真分析，最终将位移重构结果与有限元仿真结果进行对比分析。

3 升降舵壁板模拟件变形重构

飞机升降舵壁板模拟结构在位装配变形重构实验，主要模拟了分别在人工在线装配与机器自动装配两大重点装配过程中的受力变形情况。实验分为4大组，每一大组下设3组测量线，每一组测量线包含10支光纤光栅应变传感器，分别对称布置在构件的两个表面，以求完整重构出模拟件的位移变形情况。图5所示为重构实验中构件受力情况，图5（a）单点侧边1 kg加载与图5（b）单点中点10 kg加载模拟了人工在线装配过程升降舵壁板的受力变形情况，图5（c）多点侧边5 kg加载与图5（d）多点前端1 kg加载模拟了机器自动装配过程升降舵壁板的受力变形情况。

图5 模拟升降舵壁板多工况变形重构

根据以上受力变形情况，对模拟飞机升降舵壁板的构件进行有限元仿真分析，有限元模型采用ABAQUS建立，通过静力分析计算得到构件的应变和形变分别如图6和图7所示。

模拟飞机升降舵壁板构件的上下表面有对应的3组测量线，对于不同的受力情况，均对3组测量线进行位移变形重构，重构方式分别采用对端部应变进行多项式拟合的传统位移变形重构方法，对端部应变进行样条插值拟合的方法以及本文提出的基于应变误差最小化端部应变优化手段的位移变形重构方法，以上3种方法均与有限元分析得到的位移值进行对比，相应应变测量点处的位移重构点与仿真点也进行了对照，对比曲线如图8～11所示，分别展示了4种加载情况中的一条测量线的变形重构情况。

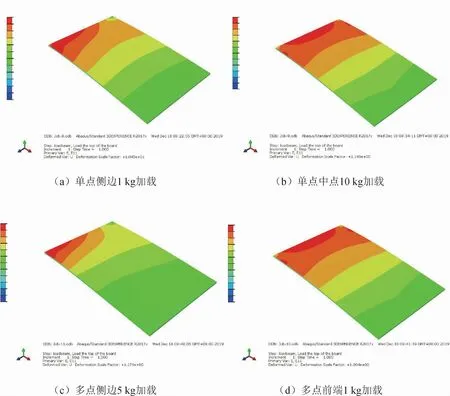
图6 模拟升降舵壁板多工况变形应变云图

图7 模拟升降舵壁板多工况变形位移云图

图8 构件单点侧边1 kg加载变形重构

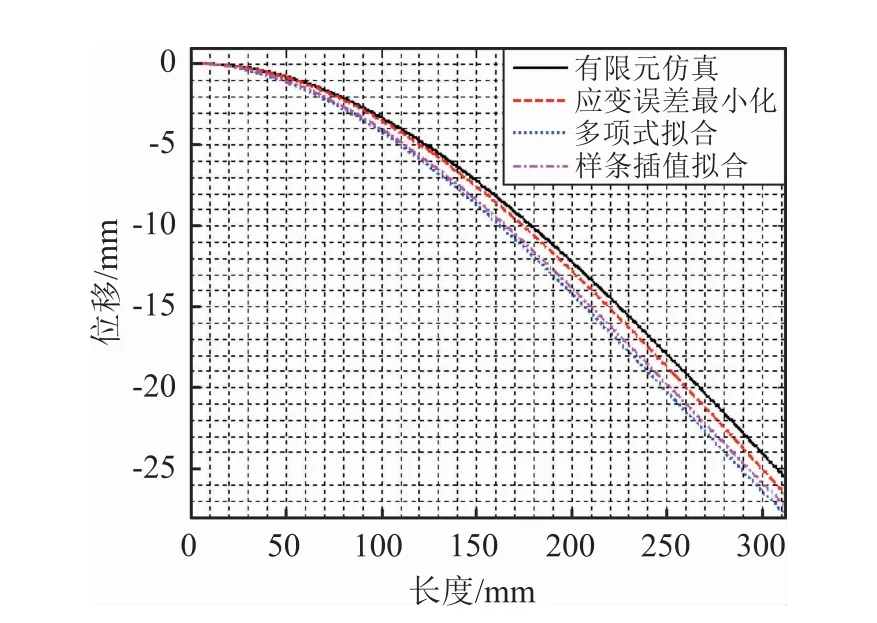
图9 构件单点中点10 kg加载变形重构

图10 构件多点侧边5 kg加载变形重构

图11 构件多点前端1 kg加载变形重构

从图线中可以明显看出，采用应变误差最小化的端部应变优化手段的位移变形重构方法的重构精度明显高于其它两种。对于单点侧边1 kg加载，单点重构误差低于5.6%，在位移变形为2.979 mm的最大变形状态下，最大位移变形重构误差值为0.1003 mm；对于单点中点10 kg加载，单点重构误差低于5.5%，在位移变形为25.95 mm的最大变形状态下，最大位移变形重构误差值为0.9126 mm；对于多点侧边5 kg加载，单点重构误差低于5.6%，在位移变形为26.41 mm的最大变形状态下，最大位移变形重构误差值为0.5693 mm；对于多点前端1 kg加载，单点重构误差低于5.0%，在位移变形为7.697 mm的最大变形状态下，最大位移变形重构误差值为0.2749 mm。

根据以上重构误差数据，基于应变误差最小化的端部应变优化的位移变形重构方法的重构精度满足飞机升降舵壁板结构在位装配过程中的位移变形的实时监测及重构要求。

4 结论

针对航空航天领域中飞机升降舵壁板结构在位装配过程中的实时变形监测的需求，本文基于传统的位移重构方式，对其结构根部应变的求取方法进行了改进，采取了一种应变误差最小化的根部应变优化求取方式，通过多种实际工况下的模拟构件实验和有限元仿真分析对比了该方式与传统拟合方式的位移重构精度，验证了该方式在飞机升降舵壁板结构在位装配过程中的位移变形重构的精确度和稳定性，整体位移点重构误差均低于5.6%，有90%的重构点的重构误差低于4%。接下来的工作将对航空航天器的更多重要零部件及其对应装配工装的在位实时变形监测进行深入的研究，以对航空航天器的高精度装配提供重要技术保障。