基于概率鲁棒的水轮机调速系统鲁棒性评估
2020-04-10刘长良王梓齐
刘长良, 曹 威, 王梓齐
(1.华北电力大学新能源电力系统国家重点实验室, 北京 102206; 2.华北电力大学控制与计算机工程学院, 保定 071003)
水轮机调速系统是涉及多学科领域的不确定系统,因此在设计控制策略时,必须保证其有着良好的鲁棒性,才能保证实际运行时系统的性能[1]。鲁棒控制在近年来得到了广泛的应用。文献[2]选择滑动模式控制对注入电网的有功/无功功率进行鲁棒控制;文献[3]应用鲁棒控制,提高了机械臂控制系统的控制系统及鲁棒性。但是如何对控制系统鲁棒性评估成为了控制界研究的重点。基于最坏情况的鲁棒性评估算法随着系统阶次的提高,计算量会大大增加,使问题求解变得极其困难[4]。
为解决这一问题,文献[5]提出了概率鲁棒的方法,用蒙特卡洛仿真来模拟系统的不确定性,通过计算性能指标的可接受概率来评价其鲁棒性。但是这种方法不能在任意性能水平下给出系统的可接受概率。针对这一问题,文献[6-7]分别使用累计频率曲线和样本标准差作为量化指标,给出了系统在任意性能水平下的可接受概率,完成了系统鲁棒性的定量评估。然而目前概率鲁棒的方法大多用来分析飞行器控制系统,并没有运用到水轮机调速系统分析中。与其他控制系统不同的是,水轮机的“水锤现象”严重影响了水轮机调速控制系统的控制品质。除此之外,水轮机机械传动机构存在明显的惯性特性,使控制系统易出现震荡和超调。
针对传统方法不能定量评价控制律鲁棒性的问题,分析水轮机调速系统的特点,以紧水滩水力发电厂为研究对象,分别设计PID 控制器和模糊内模控制器,应用概率鲁棒的方法,综合使用几种性能指标的可接受概率和统计量作为评价指标,完成两种控制器鲁棒性的定量评估,以期填补模糊内模控制和概率鲁棒分析方法在水轮机调速系统应用的空白。
1 水轮机调速系统
1.1 水轮机模型
一种能够反映引水管的水锤效应、水头和流量波动等对水轮机输出功率的影响的水轮机传递函数模型为[8]
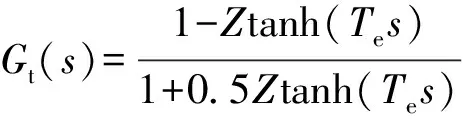
(1)

(2)
Z=Tw/Te
(3)
式中:Z为引水管阻抗;Te为水压波动时间;Tw为水流惯性时间。
若式(2)中的无穷乘积项为1,即
tanh(Tes)=Tes
(4)
则可以得到刚性水体水轮机模型;若n≥1时,可以得到弹性水体水轮机模型,在工程实践中一般取n=1。图1为弹性水体和刚性水体水轮机模型的阶跃响应曲线。
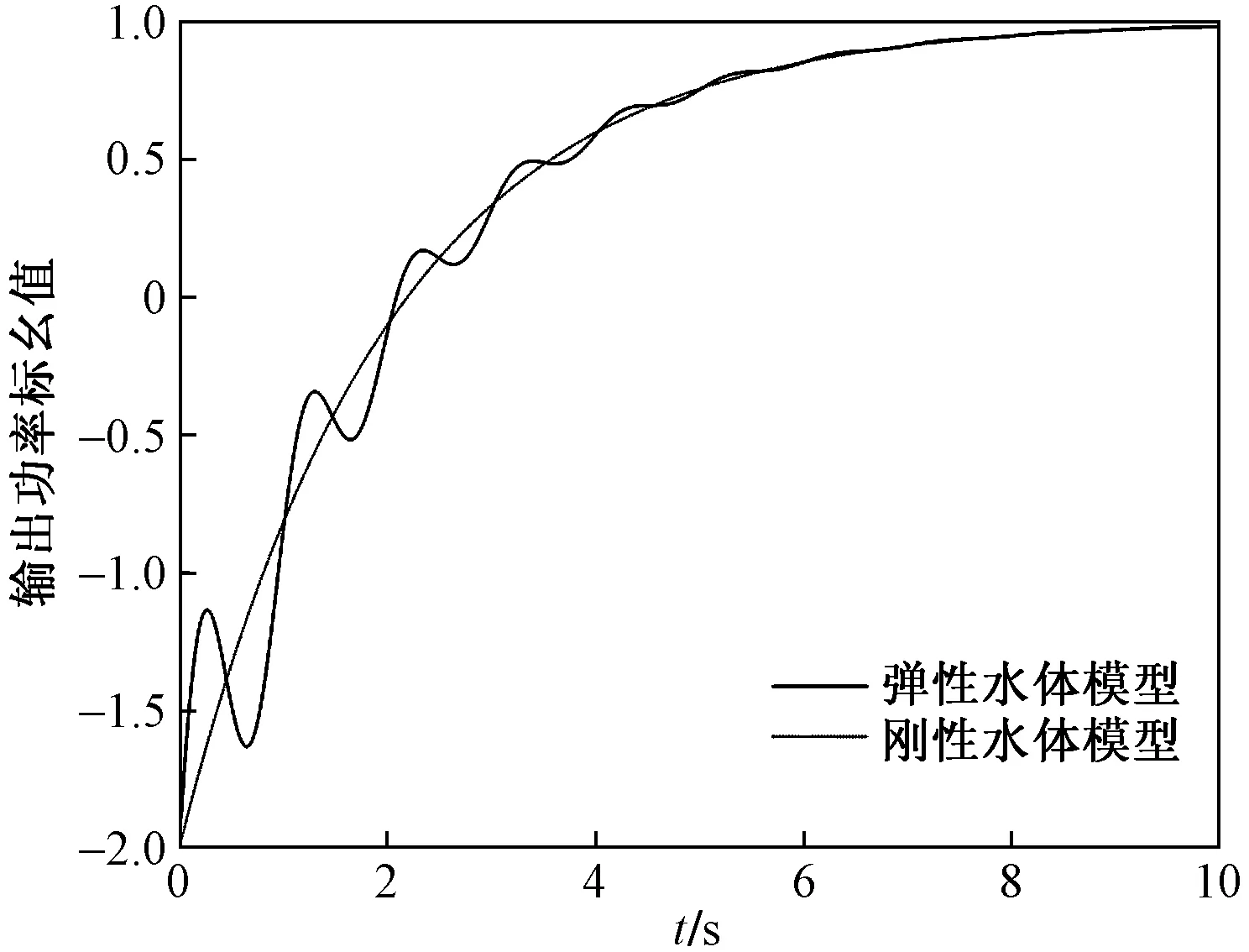
图1 刚性水体和弹性水体水轮机的阶跃响应曲线Fig.1 Step response curve of hydraulic turbine in rigid water body and elastic water body
由图1可以看出,刚性水体水轮机阶跃响应曲线是单调增加的。但是实际上,由于引水管内的水惯性作用,此时水轮机入口水头会变小,导致输出功率突然减小,即水锤作用。水锤作用会导致水轮机的输出功率经过震荡后才逐渐稳定在设定值上。当使用弹性水体水轮机模型时,能较为准确地体现水锤作用对输出功率的影响。因此,取n=1来模拟“水锤现象”对模型的影响。
1.2 液压伺服系统模型及发电机模型
水轮机调速系统水门的液压伺服系统的传递函数模型为
Gs(s)=1/[(T1s+1)(T2s+1)]
(5)
式(5)中:T1为水门伺服电机系统的时间常数;T2为液压机构的时间常数。
水轮机调速系统中与水轮机连接的同步发电机的传递函数模型为
Gp(s)=1/(Hs+D)
(6)
式(6)中:H为发电机传动惯量时间系数;D为阻尼系数。
1.3 水轮机调速系统模型
以紧水滩水力发电厂水轮机调速系统为模型。紧水滩水力发电厂发电机总装机容量6×50 MW,单管引水系统,混流式水轮机。根据运行数据,通过参数辨识得到水轮机调速系统G(s)的标称参数为:Te=0.5,Tw=4,T1=0.5,T2=0.02,H=10,D=1[9]。由式(1)、式(4)、式(5)所构成的水轮机调速系统G(s)如图2所示。

u(s)为控制器的输出,Δo(s)为水门开度变化量,ΔP(s)为水轮机输出功率变化量,Δw(s)为发电机转速变化量图2 水轮机调速系统模型Fig.2 Hydraulic turbine governor system model
2 控制策略
2.1 PID控制
PID控制作为一种成熟的控制策略,具有原理简单、调整方便等优点。PID控制器的传递函数为

(7)
式(7)中:δp、Ti、Td分别为比例带、积分时间和微分时间。PID参数整定方法有临界震荡法、Z-N法等。现使用临界震荡法,根据1.2节中G(s)的标称参数整定PID参数,得到临界比例带δk和临界周期Tk,根据表1中的经验公式,得到控制器的传递函数如式(8)所示。

表1 临界振荡法参数整定经验公式Table 1 Empirical formula for parameter tuning of critical oscillation method

(8)
2.2 模糊内模控制
内模控制(internal model control, IMC)是一种基于过程模型的控制策略,具有易设计、鲁棒性强等优点[10]。但是内模控制的可调参数少,在复杂的不确定控制系统中性能较差。
模糊内模控制(fuzzy internal model control, FIMC) 通过模糊逻辑推理对内模控制中滤波器参数进行在线调整,解决了失配情况下系统控制品质变坏的问题[11]。采用将内模控制与Mamdani二维模糊控制相结合的控制策略,以根据误差e和误差变化率de作为Mamdani二维模糊控制器的输入变量,计算内模控制器中低通滤波器的增益修正值Δk,实现在线修正。控制结构如图3所示。
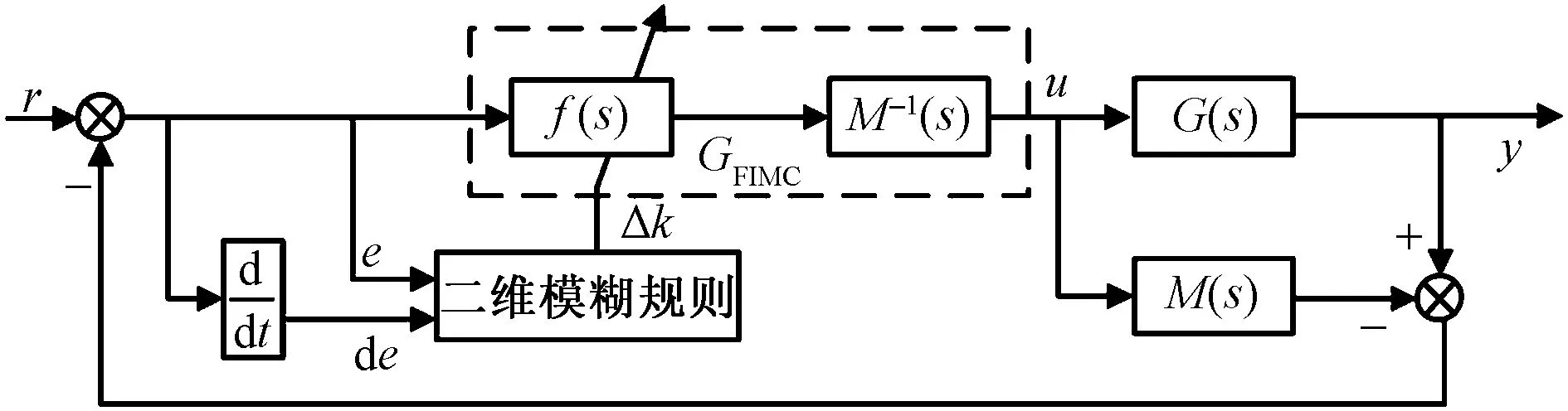
图3 水轮机调速系统模糊内模控制Fig.3 Fuzzy internal model control of hydraulic turbine governor system
图3中,M(s)为过程模型;G(s)为水轮机模型;M-1(s)为M(s)中最小相位部分的逆;f(s)是低通滤波器,传递函数如式(9)所示,其中λ=13,增益k=1+Δk;Δk为滤波器增益的修正值,取值范围为[-0.8,0.8];经过二维模糊规则修正过Δk的f(s)与M-1(s)构成了模糊内模控制器GFIMC。
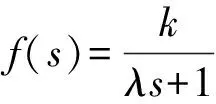
(9)
模糊规则建立的依据是:低通滤波器的增益k数值越大,响应越快,但是模型越容易失配,鲁棒性越差,越容易引起系统震荡。当误差e较大时,为了尽快减小误差,增益k应当较大;当误差e较小并且误差变化率较大时(即系统有出现超调的趋势时),为防止系统出现超调现象并缩短过渡时间,增益k应当取适中的值;当误差e较小并且误差变化率较小时(即系统缓慢趋近于设定值时),增益k应当取较小的值。
将输入e和de的语言论域都设定为{NB,NS,Z,PS,PB},依次代表{负大,负小,零,正小,正大};定义Δk的语言论域为{NVB,NB,NM,NS,Z,PS,PM,PB,PVB},代表{极小,小,较小,偏小,零,偏大,较大,大,极大}。二维模糊控制器所采用的模糊规则如表2所示。
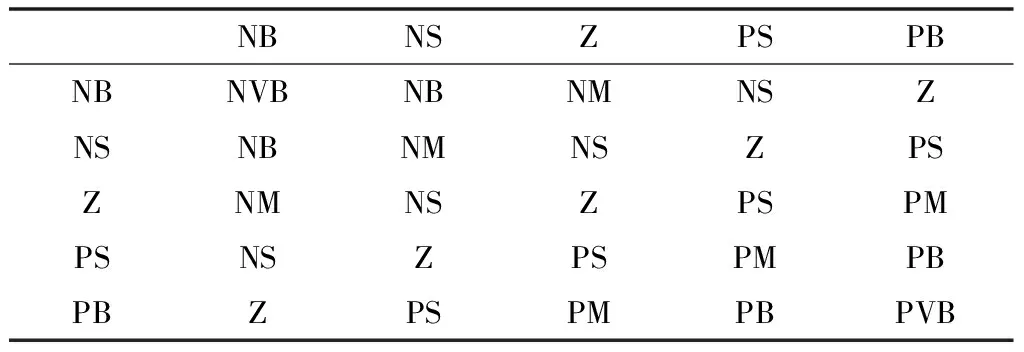
表2 模糊规则Table 2 Fuzzy rules
3 系统鲁棒性评估
3.1 概率鲁棒
蒙特卡洛是以概率统计为基础的模拟计算方法,将数学、物理、工程等领域的问题与相应的概率模型联系,进行抽样试验,进而求出所需要的统计值作为所求解的近似值[12]。
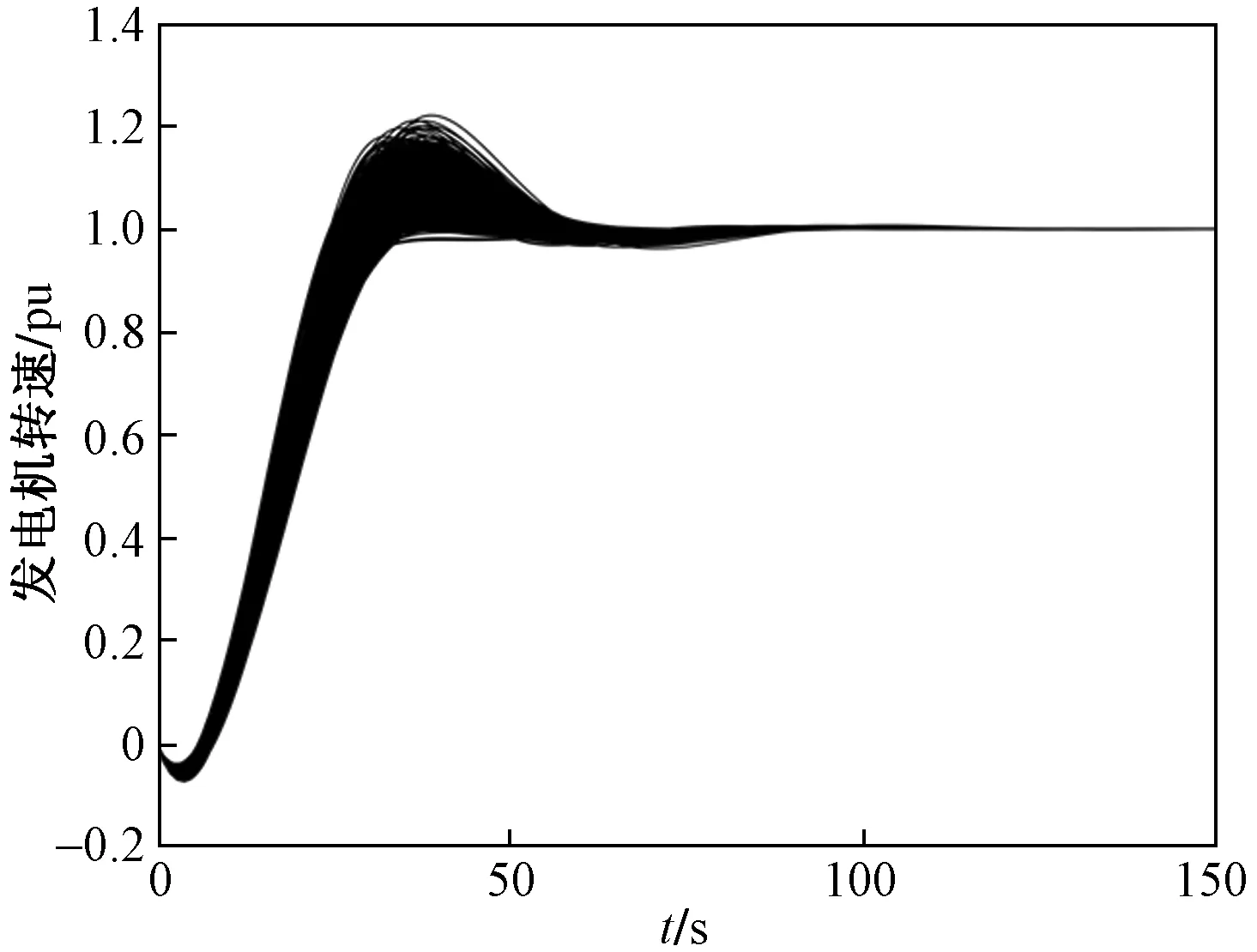
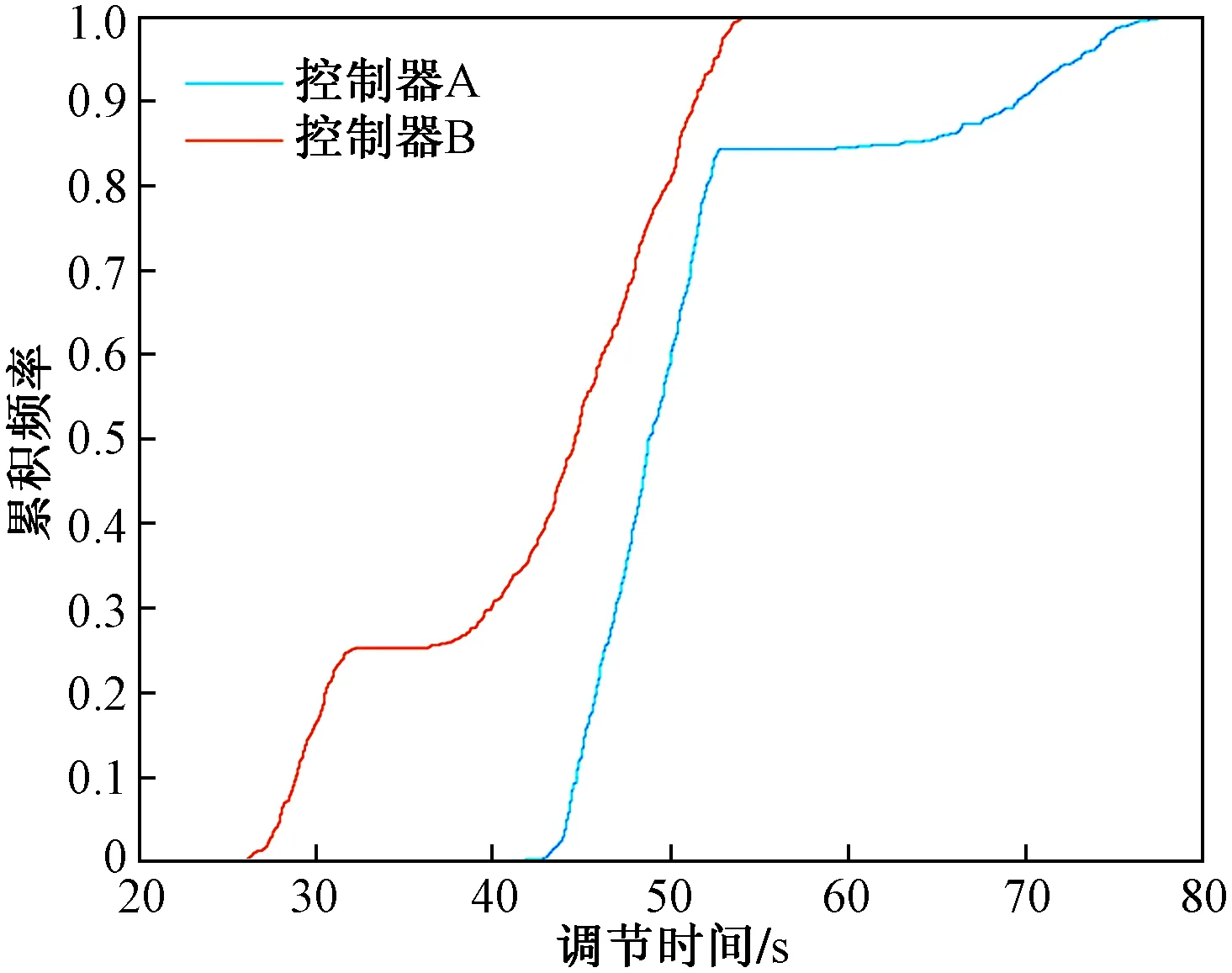
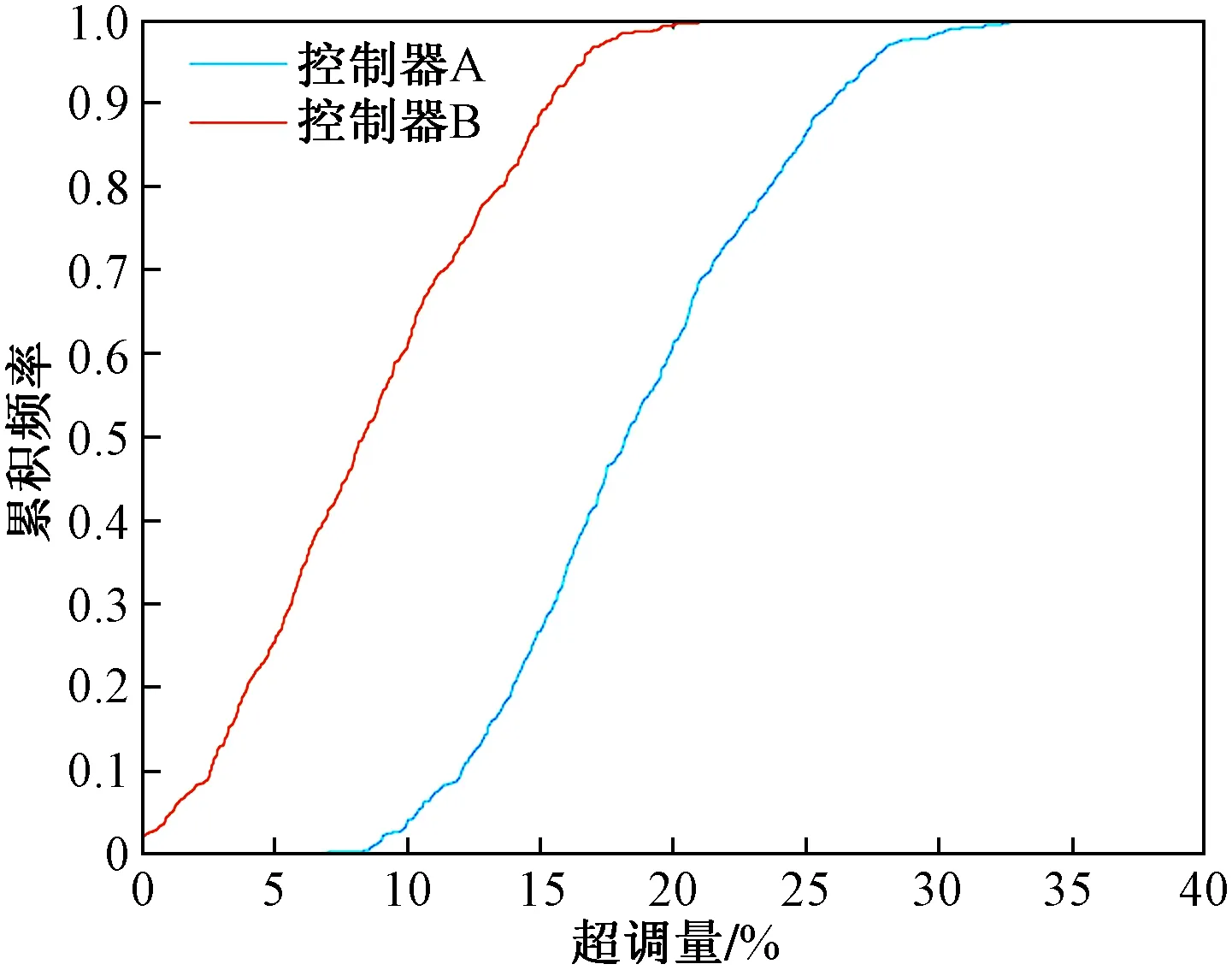
以一个闭环单入单出控制系统为例:设G(q)为系统的被控对象,q=[q1,q2,…,qn]为被控对象G(q)的n维随机参数向量且在给定的参数域中有界;随机参数向量q的概率密度函数为f(q);控制系统的性能指标为J(q);对于性能水平j,J(q) 累计频率曲线是将频率直方图的部分分段频率进行逐段积累,从而得到大于或小于某数值的概率。通过绘制性能指标J(q)的累计频率曲线,可以在给定的性能水平j下,得到累计频率曲线上某点的性能可接受概率。通过比较不同控制系统在相同性能水平下的性能可接受概率,从而衡量控制系统鲁棒性的优劣。 概率鲁棒分析的主要方法是:使用蒙特卡洛方法依照概率密度函数f(q)对参数向量q进行N次抽样;仿真生成N组系统性能指标J(q)的值;绘制J(q)的累积频率曲线并计算统计量;给定系统的性能水平j,对应累积频率曲线上的某点即为性能可接受概率P=P[J(q) 对给定的精度χ和置信水平δ,此时能够保证: (10) 成立的抽样次数N需要满足以下条件: (11) 实际应用中,概率鲁棒分析的步骤如下[13-14]: (1) 构建被评价系统的仿真模型,包括控制系统的被控对象、控制器等。 (2) 确定被控对象的随机参数向量q及其概率密度函数f(q),选择参与鲁棒性评价的系统性能指标J(q)。 (3) 确定精度χ和置信水平δ的值,通过式(9)计算抽样次数的最小值Nmin从而进一步确定抽样次数N。 (4) 对被评价系统进行N次蒙特卡洛抽样仿真,得到N组系统性能指标J(q)的值,绘制J(q)的累计频率曲线并计算样本均值μ和样本标准差S。 (5)确定性能水平j,根据J(q)的累计频率曲线计算对应性能水平j下性能可接受概率的估计值,通过性能可接受概率的估计值及样本均值μ、样本标准差S对控制系统的鲁棒性进行综合地评价。 为了评价PID控制和模糊内模控制两种控制策略在水轮机调速系统上的鲁棒性,应用概率鲁棒方法对系统进行仿真:模型的实际参数在标称参数附近以均匀分布发生±15%的摄动,选择调节时间ts和超调量σ作为评价系统鲁棒性的性能指标;取精度χ=0.01,置信水平δ=0.01,通过式(11)计算得到抽样次数的最小值Nmin=459,取抽样次数N=600。将使用PID控制的水轮机调速系统称为控制系统A;将使用模糊内模控制的系统称为控制系统B。表3为水轮机调速系统模型参数及参数摄动范围。 对控制系统A及控制系统B分别进行蒙特卡洛抽样仿真,得到水轮机调速系统控制系统A和控制系统B的阶跃响应曲线簇,分别如图4、图5所示。 表3 水轮机调速系统模型参数及参数摄动范围Table 3 Model parameters and parameter perturbation range of turbine governing system 图4 控制系统A阶跃响应曲线簇Fig.4 Control system A step response curve cluster 图5 控制系统B阶跃响应曲线簇Fig.5 Control system B step response curve cluster 通过图4和图5中的阶跃响应曲线簇可以直接看出,在标称参数发生±15%摄动的情况下,控制器A和控制器B都能保证控制系统的稳定性且控制器B的动态性优于控制器A。但仅通过曲线簇只能定性的比较控制系统的鲁棒性,无法给出一个定量的评估结果。因此,这里通过比较不同控制系统的在相同性能水平下的性能可接受概率来定量评估。系统A和系统B的稳定时间和超调量的累积频率曲线分别如图6、图7所示。 图6 调节时间累积频率曲线Fig.6 Cumulative frequency curve of settling time 从图6和图7可以看出,对于调节时间和超调量而言,控制器B的累积频率曲线整体在控制器A的左侧且横轴跨度也小于控制器A,表示其鲁棒性要优于控制器A。另外,采用累积频率曲线对系统的鲁棒性指标分别进行评价,相比阶跃响应曲线簇而言更加细致且直观。表4为应用概率鲁棒的方法对控制器A和控制器B的鲁棒性进行定量对比。其中,控制系统的性能指标选择调节时间ts和超调量σ;选择特定性能水平下的可接受概率、样本均值和样本标准差作为定量对比的指标。 由表4中可以看出,在相同可接受概率下,控制器B在调节时间、超调量、均值和标准差指标上都明显优于控制器A,说明控制器B的鲁棒性要优于控制器A。除此之外,通过可接受概率和性能指标的统计量,可实现定量比较不同控制系统鲁棒性的目的,验证了本文研究内容的可靠性。 图7 超调量的累积频率曲线Fig.7 Cumulative frequency curve of overshoot 表4 鲁棒性对比数据Table 4 Robustness comparison data 采用了基于概率鲁棒的控制律鲁棒性评估方法,通过累计频率曲线得到系统在任意性能水平下的可接受概率,结合系统性能指标可以对不同控制律的鲁棒性进行定量的评价。以紧水滩水力发电厂水轮机调速系统为研究对象,所做工作如下:①设计了PID控制器和模糊内模控制器;②应用概率鲁棒的方法对两种控制器的鲁棒性进行定量评估。得到如下结论。 (1)从控制品质角度可以看出,模糊内模控制器有着更好的鲁棒性;与基于概率鲁棒法的定量评估结果相一致。 (2)验证了概率鲁棒在控制律鲁棒性定量评估方面的有效性。 (3)对水轮机调速系统设计了模糊内模控制器,填补了模糊内模控制在水轮机调速器控制领域应用的空白。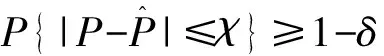

3.2 概率鲁棒分析的基本步骤
4 仿真实验



5 结论
