空心阴极热特性优化研究

1. 电子科技大学 资源与环境学院信息地学研究中心，成都 600731 2. 上海空间推进研究所，上海 201112

空心阴极是一种为离子、霍尔推力器提供电子以触发气体电离或羽流中和的装置。空心阴极的正常工作伴随着发射体温度的维持，使得整个阴极处于一种热平衡状态。这种热平衡的特性主要受限于阴极结构尺寸、材料物性等因素，而阴极整体的温度对于阴极运行的安全性、发射体工作寿命以及能耗情况有着重要影响，尤其对于高功率阴极，阴极能效是影响整个推力器工作性能的关键。空心阴极的热特性问题一直是阴极设计的关键因素。

空心阴极热特性研究始于2000年以后，最初，研究人员将重点放在阴极发射体，发现发射体的温度分布并不均匀，而是存在100～200 K左右的温度差[1-2]。此外，发射体温度与气体流率的变化有关，随流率从小增大会呈现先降低后升高的趋势[3-5]，这是阴极在不同工作模式下的热负荷变化所致。接着，Ira K[2,6]对阴极建立热仿真模型，揭示发射体的能量平衡特性，以离子和电子轰击的热流密度作为传热作用的输入条件，为整个阴极的温度分布计算提供数值方法，但该算法需先设定发射体温度，无法做到真正意义的流场与热场耦合计算。2015年以后，研究重点逐渐转向一些非传统的空心阴极：六硼化镧的无加热器阴极的发射体工作温度会低于理查森的理论预估值，Alexander推测这可能与发射体表面的化学作用或肖特基效应有关[7]；此外，一种新型发射体材料C12A7的空心阴极[8]，由于其发射体逸出功较低(0.6 eV)，可以令发射体的工作温度维持在较低的数值(400℃左右)，但这种发射体在长期工作中会出现热负荷过载的情况；而对于100 A量级的空心阴极，阴极管、发射体以及触持极都受到等离子体的撞击作用，会面临更高的热负荷威胁[9]，同时，研究人员还发现，工作下的空心阴极发射体将面临更严峻的工作寿命问题，阴极各个位置的温度升高将更为显著，这给阴极热设计带来了更高的难度。综上，关于空心阴极结构与材料对热分布特性的研究鲜有报道，这对阴极的热优化设计带来一定阻碍，然而，由于阴极热设计涉及结构尺寸、组件材料等因素的控制，使得试验研究方法的时间与经济成本较高。本文将针对阴极的热特性优化问题进行数值方法上的研究。

在传统空心阴极的热仿真中，有学者以试验测得温度作为热仿真计算中的第一类边界条件来进行空心阴极整体结构的温度分布计算[10-11]。在阴极的结构优化问题上，采用试验结果作为输入条件会降低结论的通用性以及增加研究成本。为此，本文采用单元粒子/蒙特卡洛碰撞(PIC/MCC)算法对等离子体流场进行计算(设定初始的发射体温度)，以获得阴极热计算的输入条件，再结合导热与热辐射计算模型获得空心阴极稳态工作时的热计算结果。在此基础上，考察阴极不同结构、不同组件材料对内部温度分布以及热耗散特性的影响规律。

1 数值模型

阴极在正常放电时，发射体会处于热电子发射状态，维持在一定工作温度下。在这个过程中，发射体会在几种热流密度的共同作用下维持热平衡[11]。

qi+qe+qj+qcon+qrad=0

(1)

式中：qi为由正离子轰击发射体表面所产生的正热流密度；qe为由电子轰击发射体表面所产生的正热流密度；qj为发射体发射电子所产生的负热流密度；qcon+qrad为发射体通过导热和热辐射所产生的负热流密度。需要说明的是，发射体的加热热流应包括发射体、小孔区等表面，而本文仅考虑来自发射体表面的热流，一方面由于发射体的面积远大于小孔，另一方面，离子返流的主要路径都回归于发射体表面。

本数值模型的计算思路为：1)设定发射体初始温度T0，以此作为发射体电子发射数率的初始条件；2)基于中性气体来流数率和电子发射数率，计算阴极发射体的等离子体流场分布，获得离子、电子对发射体壁面热流密度(qi+qe+qj)分布；3)以式(1)反推出qcon+qrad的数值，以此计算阴极温度场分布，获得发射体温度的新数值T0′，更新T0；4)重复至步骤1)，循环迭代计算，直至收敛。

1.1 等离子体流场计算

采用PIC/MCC混合算法对等离子体流场进行计算：PIC算法主要为实现粒子运动过程、网格内的粒子对节点分配的计算；MCC算法主要为判断粒子之间的碰撞类型，包括弹性碰撞、电荷交换碰撞、电离碰撞和中和碰撞等，具体参考文献[12]。

以中性气体来流参数和发射体电子发射参数作为输入条件，可计算整个发射区域的等离子体流场进行碰撞和运动。接着，可获得各粒子对发射体壁面的热流密度：

(2)

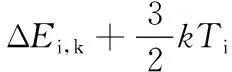
每个单元面网格内由电子轰击所产生的热流密度qe为：

(3)

式中：Ne为Δτ时间内电子撞击该表面网格的数量。这里，Ne和Ni是利用计算代码对逃逸发射体边界的电子和离子进行统计而得到的参数。

每个单元面网格内由电子发射所产生的负热流密度qj为：

(4)

式中：A0和D为常数；T0为发射体的工作温度；φ0为发射体表面逸出功，该参数根据发射体材料及表面处理的不同，大约在1.5～2.5eV之间[15]；k为玻尔兹曼常数，取1.38×10-23J/K;E为鞘层内的平均电场强度。值得说明的是，每个发射电子一般具备4kT0～12kT0的逃逸动能[13]，约为1eV，故qj恰好与发射电流密度J(A/m2)在数值上相等，该公式为考虑肖特基效应的理查森发射电流公式[14]。

1.2 温度分布计算

据前文，当qi+qe+qj的计算结果输出时，可通过式(1)得到qcon+qrad的值，从而为阴极整体温度场的计算提供第二类边界条件，同时，将环境温度(验证模型时取300 K，预估计算时取4 K)作为第一类边界条件，在上述两个边界条件下可对阴极进行温度分布的计算，计算所使用的网格划分情况如图1所示。

图1 阴极热计算的网格划分Fig.1 Mesh generation of the thermal computation in a hollow cathode

在进行表面之间辐射换热计算时，通常采用常规的四次方定律，但该方法在表面数量较多时不具备较高的计算精度和效率，为此本文引入辐射传递系数[16]。与角系数类似，辐射传递系数也是表征表面几何结构、表面间位置关系的系数。该系数反应表面A所辐射出去的能量，经过多次反射达到表面B和直接到达表面B时被吸收的能量占表面A所辐射的总能量的比例。由此，以蒙特卡洛方法结合Fortran语言编写程序代码来计算辐射传递系数。第x表面第y个单元网格对第m表面第n个单元网格的辐射传递系数可表示为：

(5)

式中：n(x,y)→(m,n)为由第x表面第y单元发射的光线经过多个表面多次反射而被第m表面第n单元吸收的光线数量；n(x,y)为第x表面第y单元所发射出的总光线数量。

第m表面第n个单元网格所吸收的净辐射热流密度为：

(6)

式中：εm为第m个表面的表面发射率；Qm,n表示第m表面第n单元网格所吸收总热辐射能量，即

(7)

1.3 计算收敛判断

以温度分布计算结果来更新发射体电子发射参数，以等离子体流场计算结果来更新qcon+qrad的值。以此进行反复迭代计算，直到当前发射体表面温度与上一次计算的残差小于0.1 K，可认为当前工况计算收敛。在给定放电电压(阳极电压)与气体来流的情况下，计算所得放电电流未必和实际参数一致，因此，为调整放电电流与实际工况一致，需要稍微调整气体来流大小，直至放电电流与真实值之间误差小于5%时，可认为当前算例计算收敛，并输出温度分布的最终计算结果。需要说明的是，在本文的计算中，当阴极处于点状模式时，计算所使用的气体流率与实际流率不会超过1 mL/min，当阴极处于羽状模式时，气体流率的计算输入值与实际值不超过0.4 mL/min。

1.4 验证试验

图2 阴极放电试验系统Fig.2 System diagram of high-current cathode discharge test

为了验证本文模型与计算代码的准确性，在真空舱中开展空心阴极的放电试验，试验系统见图2。整个试验在长1.0 m、直径0.6 m的真空舱内进行，为获得较高的真空度，以机械泵、分子泵和低温泵联合抽真空。在阴极正常工作时，真空度可以达到10-3Pa以下，保证了试验所需的高真空环境。采用k型镍铬镍硅热电偶(测温上限：1 350 ℃)对阴极外表面4个测点进行测温，采用光学温度计通过真空舱可视窗口对阴极顶进行测温，试验工况见表1，其中工况a在计算中所采用的流率值为8.6 mL/min，工况b为8.5 mL/min，工况c为8.8 mL/min。

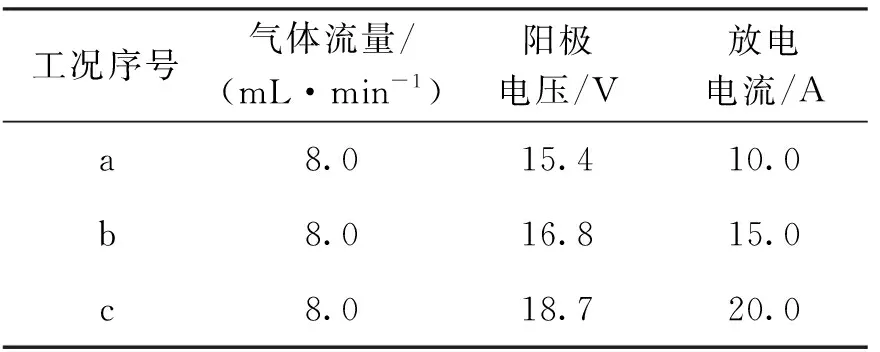
表1 阴极放电试验工况

在表1所述的3个工况下，对阴极表面4个测点(从左向右编号为1、2、3、4，见图2)以及阴极顶进行测温，并以测量结果与同工况下的计算结果进行对比，如表2所示。

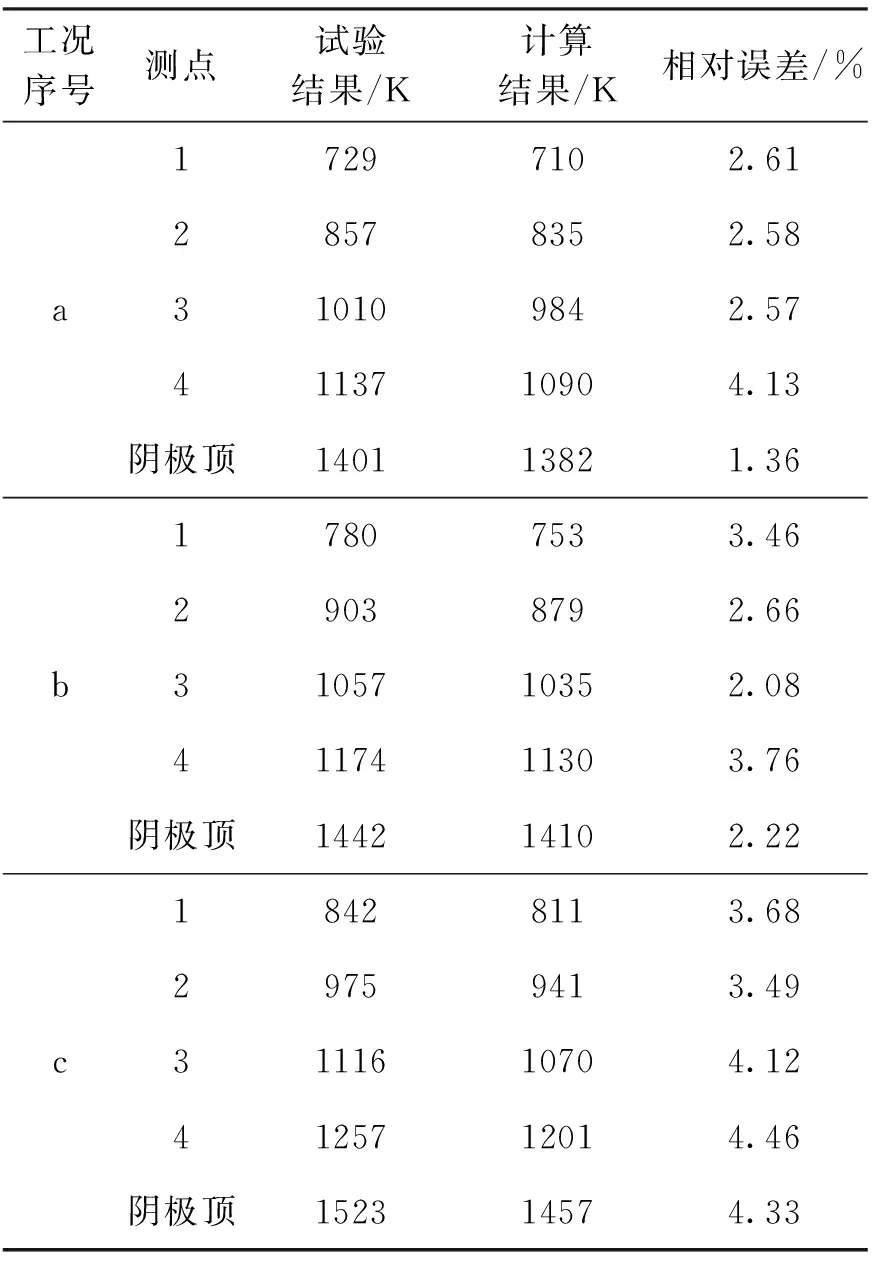
表2 试验结果与计算结果对比

表2的结果对比表明：1)最大计算误差在4.46%，平均误差为3.15%，可认为本文模型与计算代码基本可信；2)随着放电电流升高，计算结果的准确性逐渐下降(工况c的计算平均误差明显要高于工况a)，原因为经过简化的模型无法将高电流下阴极内部的放电、传热过程精确描述，同时忽略各个焊点处的电阻与热阻也会带来一定误差，并且上述两种误差在温度升高时会更加显著。

2 计算结果分析

对阴极整体温度分布的计算目的有两点：1)获得不同结构、材料阴极的内部温度分布的特点；2)揭示不同结构、材料对阴极热耗散的影响规律。为此，将阴极的结构、材料分为4个影响因素，分别讨论每个因素对阴极温度分布的影响规律。本节采用的阴极结构如图3所示，该结构与验证试验所用阴极结构有很大差别。放电电流设置为10 A，阳极电压为20 V，要维持放电电流不变，发射体温度几乎恒定。

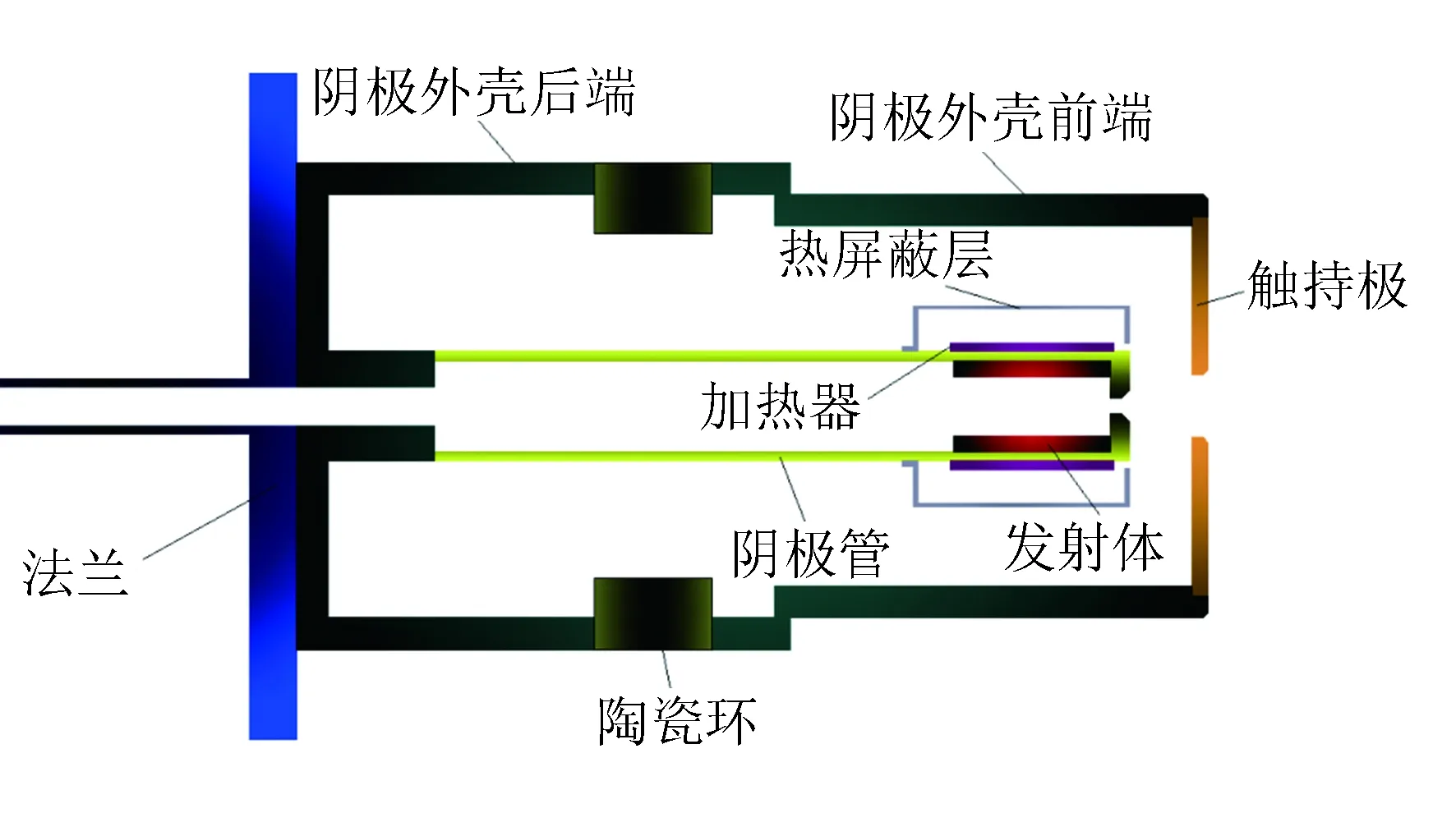
图3 阴极结构示意Fig.3 Schematic diagram of cathode

2.1 阴极长度

为研究阴极整体长度对温度分布以及热耗散的影响，在不改变阴极其他组件结构的情况下，单独增加陶瓷环右端的阴极管与外壳前端的长度，分别对阴极整体长度为l=12 cm到l=17 cm(步长为1 cm)的6组算例进行计算，计算结果见图4和图5。

图4结果表明，当阴极整体长度增加时，阴极前端组件温度有微小下降趋势，而阴极后端组件温度下降较为明显。原因为:从传热角度来说，当阴极长度增加时，阴极前端组件主要受到来自发射体区域的热辐射影响，该区域的传热过程几乎不受影响；而阴极后端组件会受到来自前端导热与热辐射的双重影响，进而主要导致阴极管导热热阻增加、外壳散热面积增大，这两者都会导致后端温度下降。

图5表明，在阴极长度从12 cm到17 cm的变化中，阴极整体热耗散功率呈现出先减小后增大的趋势。该现象的机理较为复杂，当阴极长度增加时，会同时增加阴极外表面辐射能力和阴极内部的导热热阻，但是，前者有助于热耗散，而后者会阻碍热耗散。在阴极长度较短时，增加阴极长度对内部导热热阻的影响要大于对外表面辐射能力的影响，于是出现热耗散暂时降低的情况；而在阴极长度较长时，情况刚好相反。值得注意的是，上述的热耗散功率极值点并非仅在本文阴极工况中存在，只要阴极的结构依然属于典型空心阴极的范畴，那么从机理上来说，这样的极值点必然会存在，不同的是，阴极各组件结构或材料变化会影响该极值点的位置。因此，在空心阴极的优化设计中，应充分考虑该极值点，以提高能效。

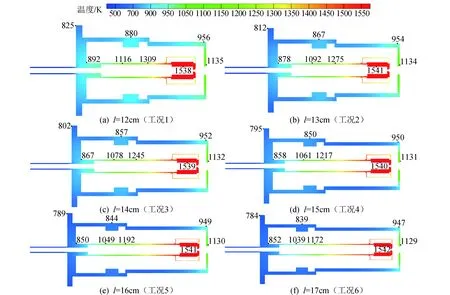
图4 不同长度阴极的温度分布云图Fig.4 Contours of temperature distribution for different-length cathodes

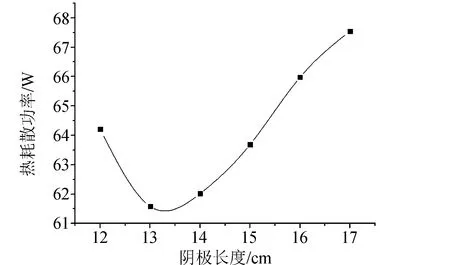
图5 不同长度阴极对应的热耗散功率Fig.5 Thermal consumption power of different-length cathodes

2.2 热屏蔽层结构

为研究不同热屏蔽层(简称热屏，下同)结构对阴极温度分布以及热耗散的影响，将阴极热屏划分为单层(工况1)、双层(工况7)、3层(工况8)、4层(工况9)以及半封闭(工况10)结构进行计算，计算结果如图6和表3所示，各热屏之间是严格非接触结构。

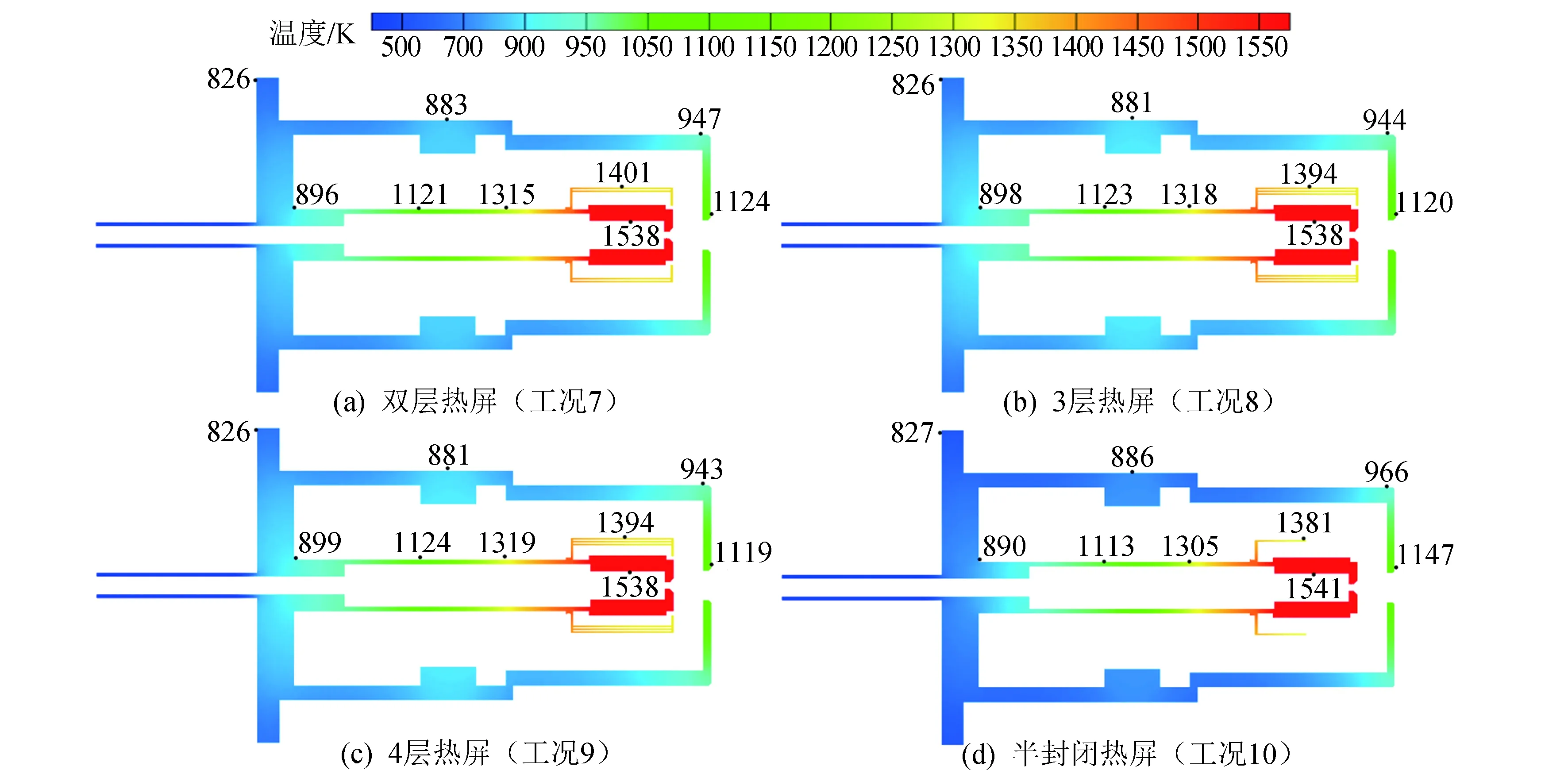
图6 不同热屏结构阴极的温度分布云图Fig.6 Contours of temperature distribution of cathode for different-structure heat shields

通过图4(a)、图6(a)(b)(c)对比表明，当热屏层数增加时，整个阴极前端的组件温度下降，后端的整体温度略有上升。原因为：当热屏层数增加时，热屏的保温作用增加，使热屏表面温度下降，进而使其表面辐射换热能力下降，对阴极前端的热量供给降低。但是，发射体的热量通过前端热辐射的散热途径受到阻碍时，却在后端通过导热途径散热时得到了增强，因此，阴极后端的阴极管、法兰的温度均有不同程度的升高。图4(a)与图6(d)对比表明，当热屏结构改为半封闭结构时，阴极前端组件温度升高，而后端的组件温度下降，与热屏层数增加时的结果刚好形成相反趋势。这表明发射体通过热辐射传递给阴极前端组件的热量增加，而对后端传递的热量减少。

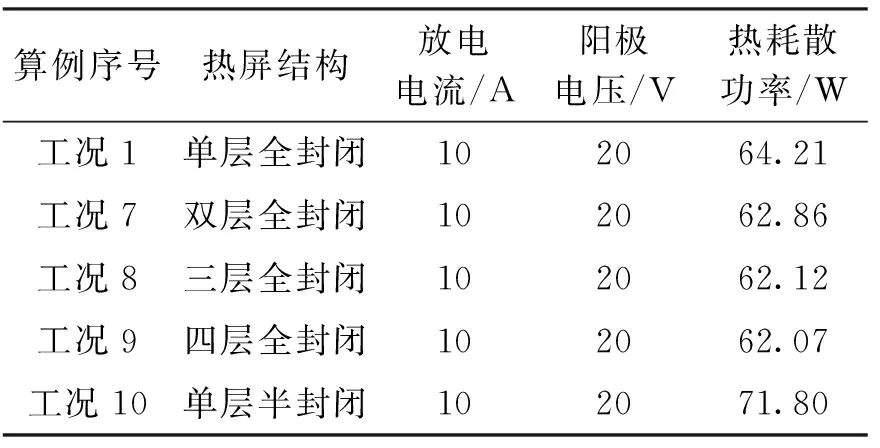
表3 不同热屏结构阴极的热耗散数据

表3结果说明，尽管在热屏结构改变的同时，阴极内部传热过程会发生此消彼长的变化，但是，随着热屏结构由单层半封闭到单层全封闭，再到四层全封闭的改变过程中，阴极整体热耗散在逐渐降低，这说明热屏层数增加、封闭程度提高都有助于保温作用的提高，尤其当半封闭结构变为全封闭时，热耗散功率降低了7.6 W左右。但值得注意的是，随着热屏层数的增加，热耗散功率呈现了一种减速降低的趋势，这意味着热屏层数增加所带来的保温作用在逐渐降低，在优化设计时应考虑到该趋势，并适当增减热屏层数。

2.3 外壳表面处理方式

阴极外壳的表面状况对阴极向外环境的辐射换热有直接影响。以常用材料瓷封合金4J34[17]为例，对采用不同表面处理的阴极外壳工况进行热仿真计算，具体包括未处理表面(工况1)、光滑表面(工况11)以及严重氧化表面(工况12)，计算结果见图7和表4。

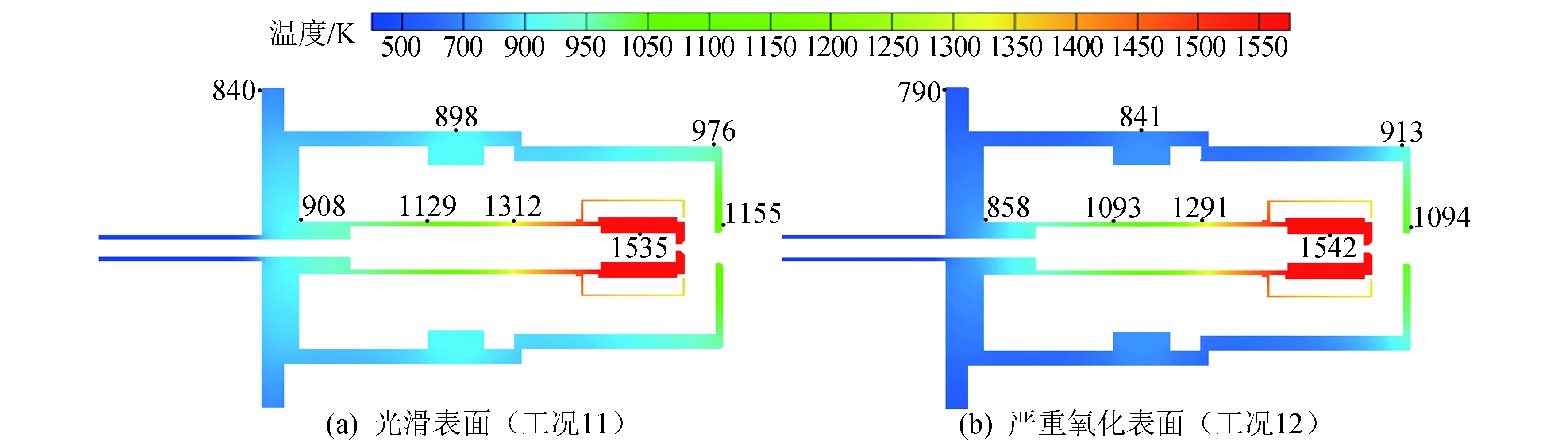
图7 不同外壳表面处理阴极的温度分布云图Fig.7 Contours of temperature distribution of cathode with different surface treatment on its shell

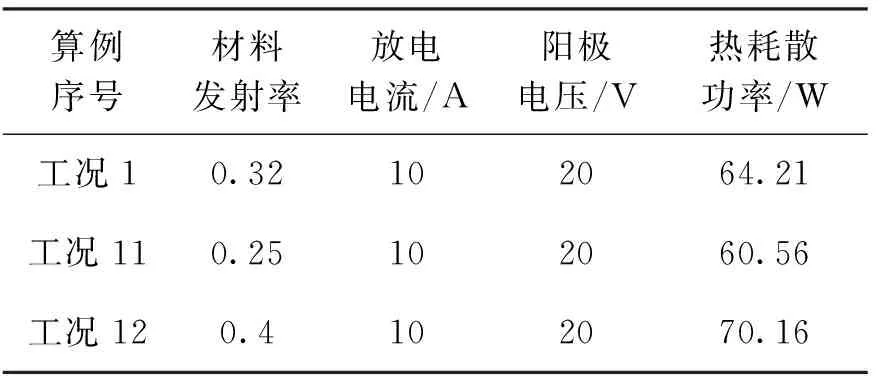
表4 不同外壳表面处理阴极的热耗散数据

计算结果表明：在3种表面状况中，工况11各组件温度最高，工况1次之，工况12最低(见图7与图4(a))；工况12的热耗散最高，工况1次之，工况11最低(见表4)。原因为：材料表面发射率的降低可以削弱表面热辐射散热，但当表面热流密度降低时，表面温度就会随之升高。需要说明的是，表面温度升高会提高辐射换热功率，而表面发射率的降低会降低辐射换热功率，但两者的共同作用最终会使辐射换热功率降低，这说明发射率是主要诱因，揭示出外壳表面处理方式对阴极传热过程的影响特点。

2.4 阴极管材料

阴极管材料通常选用耐高温的金属材料，如钼(工况1所选材料)、铌、钛的合金等[17-18]。同样地，在图8和表5中，分别给出阴极管为铌和钛的计算结果。

通过工况1、工况13与工况14的对比，工况1中除发射体外的各组件温度最高(见图8与图4(a))，工况13次之，工况14最低；并且，工况1的热耗散功率最高，工况13次之，工况14最低(见表5)。导致该结果的原因与3种材料的热导率有关。工况14中阴极管热阻最高，工况13次之，工况1最低，因而工况14中发射体对其它组件的热传导阻力最大，工况13次之，工况1最低。因此，工况14中其他组件获得发射体传递出的热量最低，所以温度与热耗散相对较低，工况13与工况1同理。通过上述分析，可引申出一个更具普遍意义的推论：如果阴极中任何一个组件使用较低的热导率材料时，都可以增加阴极某局部的传热热阻，导致整体温度以及热耗散的降低。

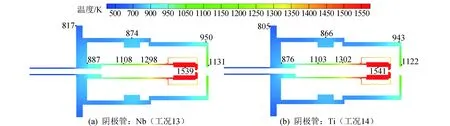
图8 不同阴极管材料阴极的温度分布云图Fig.8 Contours of temperature distribution of cathode with different cathode tube materials

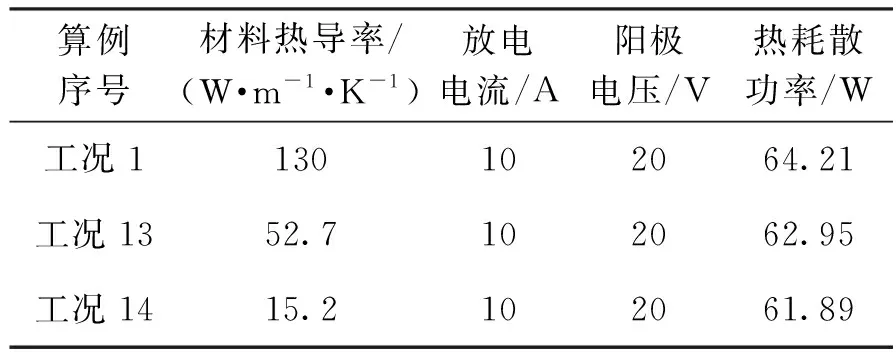
表5 不同阴极管材料阴极的热耗散数据

根据外壳表面处理方式与阴极管材料的分析，若使热耗散功率降低，可采用光滑表面的阴极外壳或热导率较低的阴极管，但两者有所不同：1)外壳表面处理方式对阴极热耗散的影响比阴极管材料要显著，外壳表面处理后热耗散功率变化幅度在7%左右(见表4)；2)外壳表面处理方式在降低热耗散功率的同时却升高了阴极整体温度，这对阴极内部某些连接处会带来较高的热应力，是一种负面效应，而阴极管材料则相反。在设计选材时，应充分考虑上述情况。

需要说明的是，阴极热耗散功率确实占阴极整体放电功率较高的比例，但对于阴极的总放电功率来说，除了热耗散，还包括电子对阳极壁面的能量沉积、光能、中性气体的动能增量以及各壁面削蚀所消耗的能量等，因此，优化阴极放电性能的主要方法都集中在如何降低无用功耗方面。

3 结束语

本文采用等离子体流场计算数据与温度场计算数据互为输入条件，进行反复迭代的算法，对空心阴极整体的温度分布以及热耗散功率进行了数值计算，获得不同阴极结构、不同材料对阴极温度分布以及热耗散的影响规律，主要结论如下：

1)随着阴极整体长度由小增大，阴极除发射体外的组件温度均有不同程度降低，但热耗散功率会呈现出先减小后增大的趋势，期间一定存在极小值点；

2)当阴极热屏层数增多时，阴极温度分布呈现前端降低、后端升高的趋势，而热耗散功率呈现出减速下降趋势，当热屏变为半封闭结构时，阴极整体热耗散功率升高11.8%；

3)当阴极外壳选用发射率较低的材料时，除发射体外的各组件温度均有升高，而热耗散功率下降，当阴极组件选用热导率较低的材料时，除发射体外的各组件温度以及总热耗散功率均会降低。