基于SPH方法的球形贮箱液体晃动动力学分析

马骏骁1，马亮，魏承，*，胡月，赵阳

1. 中国空间技术研究院 通信卫星事业部，北京 100094 2. 哈尔滨工业大学 航天工程与力学系，哈尔滨 150001

随着航天器的持续飞行，贮箱内的燃料也在不断消耗，理想情况为贮箱内燃料含量由充满状态至耗尽状态。不同的燃料含量意味着液体质量的不同，从而导致液体由于晃动对贮箱产生的力和压强的不同。贮箱内液体燃料的含量总是处于变化之中，不同含量的液体燃料产生的晃动行为会具有怎样的差别，需要进行对比分析。光滑粒子流体动力学方法(SPH方法)自1977年由Lucy[1]和Gingold[2]首次提出。基于SPH方法的流体动力学问题研究经历了逐步完善的过程：Monaghan[3]于1994年首次将SPH方法引入流体动力学问题的求解，随后多位学者基于此方法对钝体绕流[4]、剪切流动[5]、溃坝[6]等问题进行了仿真分析。同时，SPH方法在计算精度[7]、计算稳定性[8]及边界处理[9]等方面经过不断的改进和修正，使其成为一种解决流体动力学问题的成熟建模方法。

液体晃动问题主要具有三类研究方案：理论研究、数值研究、试验研究。理论研究中，最为常用的方法为等效模型方法，但等效模型不足以准确地捕捉自由表面的形状，使其无法描述晃动液体的实际几何形状。数值研究以计算流体动力学(CFD)为主，但无论哪种CFD方法，都无法对大幅液体晃动进行准确描述，尤其当液体发生破碎等强非线性现象。试验研究多用于验证建模方法的准确性或对比分析防晃结构的优劣，但试验方法成本太高，且受多种试验因素制约，对部分试验条件难以模拟，因此无法大规模应用。由此对于液体晃动问题，无网格的SPH方法得到了快速的发展与应用。刘富[10]基于SPH方法对飞机油箱进行晃动分析，并提出晃动抑制方案。朱小松[11]则将并行计算引入SPH方法，试图提升仿真效率。张凯凯[12]建立液体晃动试验平台以验证SPH数值模型的正确性，在此基础上对机翼油箱的防晃结构进行优化设计。章恒[13]针对流固耦合问题，采用SPH方法通过改进流动模拟算法及耦合处理算法，对常见场景进行模拟仿真，验证了算法的正确性。杜林霏[14]通过改进传统SPH方法中压强、边界等方面的处理方法，同时给出SPH模型的晃动力、力矩计算方法，对二维半圆形贮箱的晃动问题进行仿真分析。聂霄[15]通过并行计算理论分析了不可压缩流(ISPH)的晃动现象。李清[16]则分别采用了理论方法、SPH方法、试验方法对贮箱晃动稳定性进行了分析。上述分析均缺乏对三维球形贮箱的仿真研究，而这正是本文的重点研究内容。

本文针对航天器球形贮箱内的液体晃动问题，采用SPH方法进行建模仿真，建立不同仿真需求的航天器球形贮箱模型。通过记录贮箱受力情况及设置测量点压强情况，对不同仿真参数进行影响分析，并最终得到相应规律，从而为航天器球形贮箱的设计提供技术依据。

1 基于SPH方法的流体动力学建模

1.1 SPH方法近似原理

SPH方法的核心近似原理包括核近似、粒子近似，如图1所示，图中k和h表示光滑因子和光滑长度。核近似的目标是通过构造适合的光滑函数(核函数)，近似等效替代狄拉克函数，从而将任意函数表示为积分形式。粒子近似的过程就是将积分计算离散为求和计算的过程，光滑半径控制求和范围。通过上述两步近似，任意函数及其导数即可在SPH理论框架内由结构更简单、求导更方便的核函数进行计算求解。

图1 SPH方法核心近似原理Fig.1 The core principle of approximate SPH method

(1)核近似

核近似是SPH方法近似过程的第一步，利用狄拉克函数的性质，将任意函数表示为积分形式。设任意函数f(x)，x为空间位置向量，该函数可表示为一种含有狄拉克函数的积分形式：

(1)

式中：x′为定义域内某一空间位置向量，Ω为体积分域，δ(x-x′)为狄拉克函数，δ函数定义为：

(2)

由于δ函数“虽连续但不可导”，构造一种光滑函数(核函数)W(x-x′,h)替代δ函数，如图1(a)所示。将核函数代替式(1)中的δ函数，则任意函数f(x)表示为：

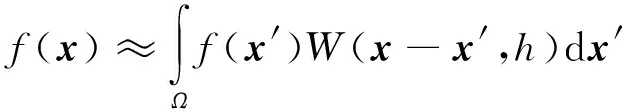
(3)

式(3)中方程为约等，这是由于核函数不能完全等价于狄拉克函数，可以通过泰勒展开证明采用核函数替代的任意函数积分表达式具有二阶精度。

·[f(x′)W(x-x′,h)]dx′-

(4)

采用散度定理，对式(4)中第一项进行积分变换，将体积分变为面积分，可以得到：

(5)

式中:n是面域S的单位法向量。当核函数支持域处于问题域内部时，面积分项为零,可以得到：

(6)

当核函数支持域与问题域存在重叠时，面积分项不为零，由此引发SPH方法的边界问题。

(2)粒子近似

粒子近似是SPH方法近似过程的第二步，粒子近似的核心就是离散化，将积分运算离散为求和运算。式(3)通过粒子近似可推导为：

(7)

式中：j为粒子i支持域内的任一粒子;mj为粒子j的质量;ρj为粒子j的密度;j=1,2,…,N,N为粒子i支持域内粒子总数，如图1(b)所示。因此，粒子i处的函数值可最终表达为：

(8)

式中：Wij=W(xi-xj,h)。式(6)也可通过粒子近似推导为：

W(x-xj,h)

(9)

粒子i处的函数空间导数值可最终表达为：

iWij

(10)

SPH方法实际是将对任意函数的运算转化为对核函数的运算，由于核函数结构简单,易于求导，从而达到了简化运算的效果。

1.2 N-S方程求解

流体属于连续介质，因此需遵守连续介质方程组，即Navier-Stokes方程组。N-S方程组包括：

1)连续性方程,

(11)

2)动量方程,

(12)

式中：t为时间；v为速度向量；ρ为密度；σ为应力张量；α和β均代表三个坐标轴方向。上述方程未体现外力及能量交换的情况，但并不影响后续SPH方法的应用。对N-S方程组分别进行SPH离散近似，将方程等式右侧的偏微分项转换为核函数的偏微分，从而得到SPH形式的离散化N-S方程组。

(1)连续性方程

应用式(10)对方程(11)等式右侧的速度偏微分项进行SPH离散近似，可以得到：

(13)

由于单位空间导数存在如下表达形式：

W(x-x′,h)dx′=

(14)

经整理计算，可以得到SPH离散近似后的连续性方程：

(15)

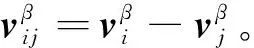
(16)

方程(16)为最常用的SPH离散化连续性方程。从方程的结构可以看出，流体密度的时间变化率与粒子质量、粒子间的相对速度有关，同时也与核函数的偏导数有关。

(2)动量方程

应用式(10)对方程(12)等式右侧的应力张量偏微分项进行SPH离散近似，可以得到：

(17)

由式(14)可知存在以下恒等式：

(18)

将式(18)与式(17)相加，则得到经SPH离散近似后的动量方程：

(19)

经整理后最终可以得到：

(20)

方程(19)与方程(20)均为常用的SPH离散化动量方程。从方程的结构可以看出，流体速度的时间变化率与粒子质量、粒子密度、粒子应力张量均有关，同时也与核函数的偏导数有关。

1.3 SPH方程相关计算

采用SPH方法通过离散近似得到了连续性方程、动量方程、能量方程的离散形式，为得到最终的计算结果，相关的计算问题需要得到进一步解决：核函数的构造与选择、应力张量的分解与计算、边界问题的处理等问题。

(1)核函数

核函数是SPH方法的核心概念，准确地构造满足条件的核函数是SPH方法不断发展的核心驱动力。本文采用B样条核函数[17]。核函数的支持域由光滑长度h及光滑因子κ决定，支持域半径为κh。B样条核函数表达式：

W(R,h)=αd×

(21)

式中：αd=1/4πh3。

(2)应力张量

对于离散化连续性方程，核函数表达式确定后即可进行求解计算。但对于离散化动量方程，还需解决应力张量的计算问题。应力张量一般代表流体介质的本构方程，由压强项及粘度项组成，目前主流的计算方案是通过状态方程及人工粘度对其进行计算求解。以动量方程(19)为例，可将应力张量分解，得到如下形式的动量方程：

(22)

式中：pi,pj分别表示粒子i,j处的压强；Πij代表粒子i,j间的人工粘度。

(3)边界处理

为解决边界问题，SPH方法引入虚粒子，这种类型的粒子一般位于问题域边界之外，主要用于解决距问题域边界一个支持域半径长度内发生截断的流体粒子的边界问题。

图2描述了SPH方法中的几种粒子类型及其相对位置关系。其中，粒子3，8代表边界粒子；粒子4，7代表发生截断的流体粒子；粒子5，6代表未发生截断的流体粒子；空心粒子(粒子1，2，9，10)代表虚粒子。粒子5，6距问题域边界不小于kh，粒子4，7距问题域边界小于kh，虚粒子位于问题域边界以外。虚粒子一般不具有物理参数且不带入SPH方程中进行计算，部分特殊虚粒子即使具有物理参数且代入SPH方程，下一仿真时刻虚粒子也不会按照计算结果移动，而是根据初始设置保持固定或按照一定规律运动。

不同边界问题处理方案的主要差别在于设置具有不同作用的虚粒子。

图2 支持域与问题域截断导致边界问题Fig.2 Boundary problem caused by the overlap of support domain and computainal domain

图3所示为动态粒子边界。在此边界问题解决方案中，虚粒子被设置为多层动态粒子，虚粒子位于问题域边界及边界外的区域，虚粒子厚度与支持域半径相关。动态粒子边界的特殊性在于动态粒子与流体粒子共同代入SPH方程，用于场变量的离散近似计算，从而提高边界处的SPH计算精度。但动态粒子在每时间步长下的计算结果不代入下一时间步长，而是按照仿真设置保持静止或按照一定规律运动，这也使得动态粒子边界适合用于含有复杂边界或运动边界的流体仿真问题。

图3 动态粒子边界Fig.3 Dynamic particle boundary

后续仿真任务涉及球形贮箱，并会在贮箱内设置不同类型的防晃挡板，因此本文选择动态粒子边界[18]作为边界问题解决方案。

1.4 贮箱受力计算

液体晃动现象同样对贮箱产生力的作用，进而影响携带贮箱的火箭、卫星等航天器的动力学行为。因此，需同样监测贮箱的受力情况，设置一定的防晃措施，减小贮箱受力。建模仿真过程中，需要计算贮箱受力，贮箱结构由离散的边界粒子等效，计算贮箱受力实际上是计算边界粒子所受合力。边界粒子作为虚粒子会被代入流体粒子的动量方程中进行计算，反过来同样可以将流体粒子代入边界粒子的动量方程进行计算，方程表达为：

(23)

式中：下标b和f分别代表边界粒子量和流体粒子量。上式得到一个边界粒子的数值加速度值，将所有边界粒子的加速度与自身质量相乘再求和，即可得到贮箱的受力F：

(24)

2 仿真试验结果与分析

2.1 模型建立

(1)液体体积

本文采用的球形贮箱半径设置为r=0.125 m，贮箱设置为刚体。由于液体体积的变化会改变液体对贮箱的作用力，针对仿真需求设计如图4所示的5种含有不同体积液体的球形贮箱模型。5种模型的贮箱运动模式设置为正弦运动，速度曲线方程为vy=0.12πcos(3πt)，且保持不变。定义液面高度h为贮箱内液面至贮箱底部的距离，通过设置不同的液面高度值实现不同的液体体积。液面高度分别设置为h=0.05 m,0.075 m,0.1 m,0.125 m,0.15 m，如图4(a)～(e)所示，图中数值单位为m。

(2)挡板设置

贮箱内的液体晃动现象需要受到抑制，是否设置挡板及挡板的安装位置变化均会改变液体对贮箱的作用力，针对仿真需求设计如图5所示的一种不含挡板及4种含有不同安装位置挡板的球形贮箱模型。挡板同样设置为刚体，且位于xoz平面。以上5种模型的贮箱运动模式设置为正弦运动，速度曲线方程为vy=0.12πcos(3πt)。液面高度设置为h=0.1 m，且均保持不变。定义挡板高度hb为挡板上边至下边的距离，挡板位置hp为挡板下边至贮箱底部的距离。挡板高度设置为hb=0.05 m，且保持不变。挡板位置分别设置为hp=0 m,0.025 m,0.05 m,0.075 m，如图5(a)～(e)所示，图中数值单位为m。

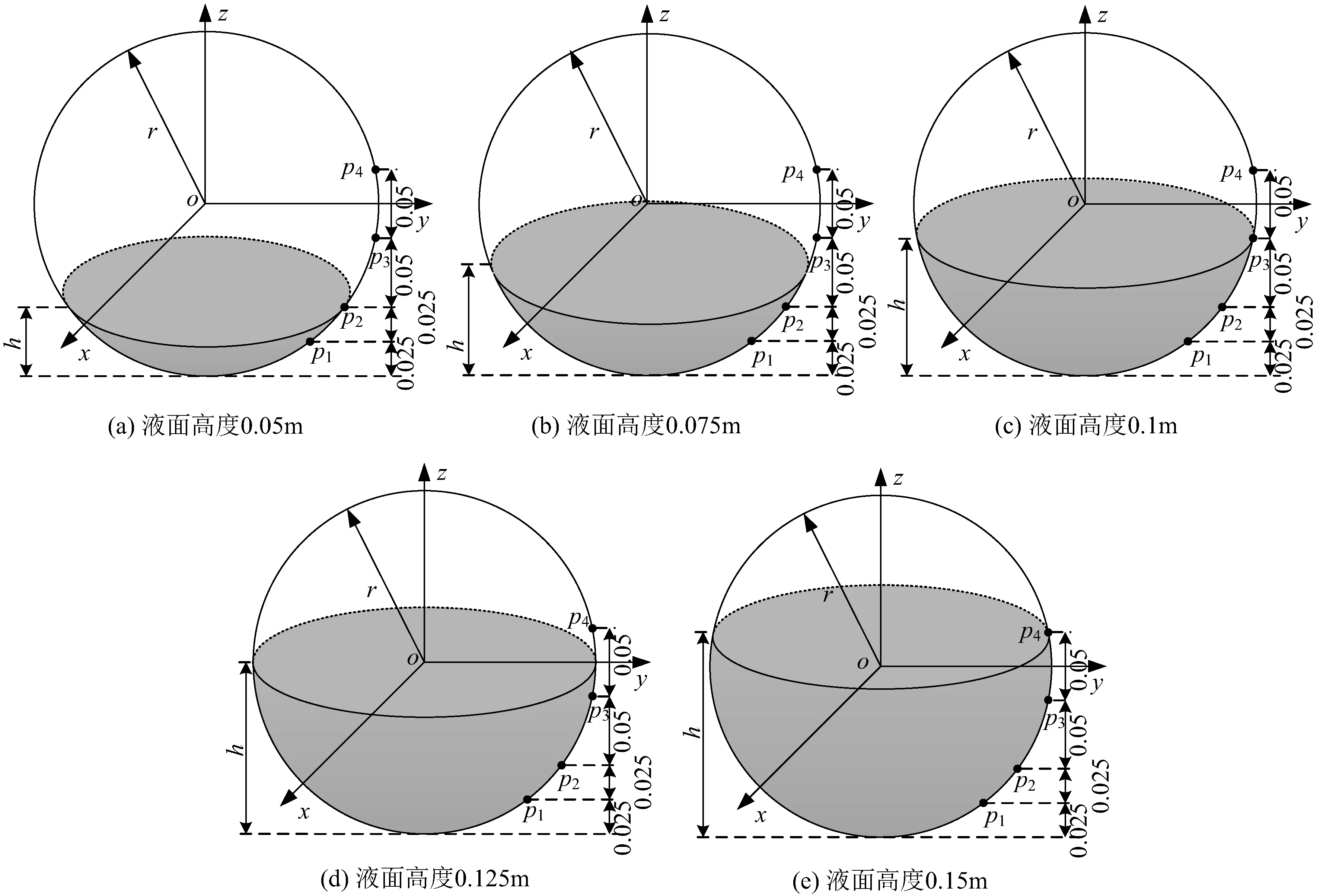
图4 不同液体体积贮箱模型Fig.4 Tank models of different liquid volume

图5 不同挡板设置贮箱模型Fig.5 Tank models of different baffle positions

2.2 仿真结果分析

本文主要分析球形贮箱的受力情况及局部压强情况。由于贮箱运动仅发生y轴方向，液体在yoz平面的晃动行为明显，因此主要分析贮箱y,z两轴方向的受力情况。贮箱内设置4个测量点，均位于yoz平面。测量点在高度范围需分布均匀且涵盖贮箱重点受压区域，因此测量点按照图4(a)～(e)及图5(a)～(e)中所示位置进行设置，各仿真工况的粒子数及仿真时间如表1所示。

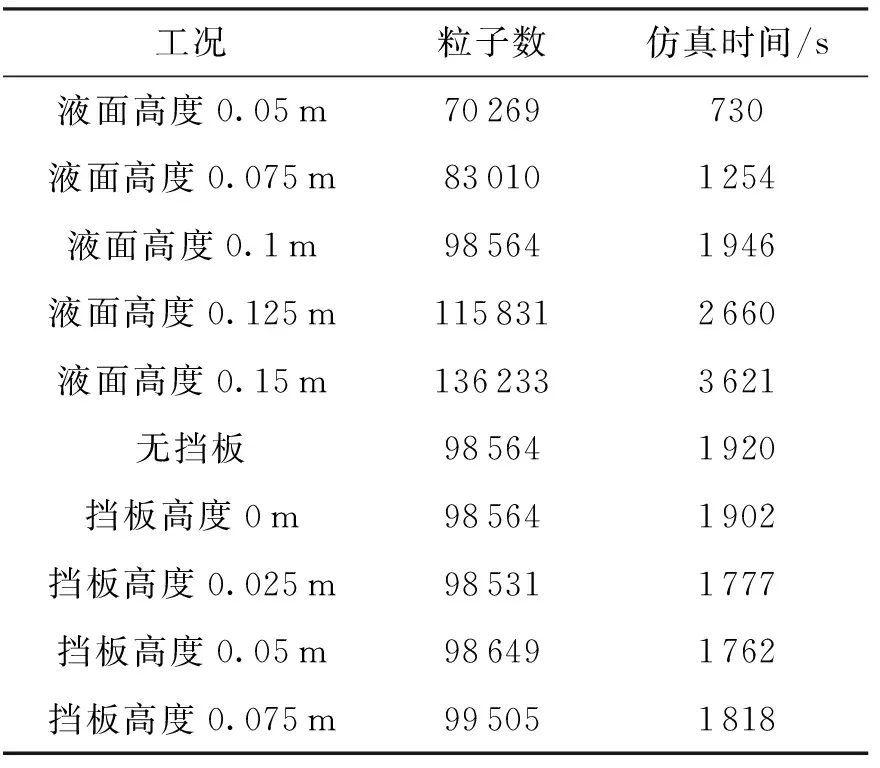
表1 粒子数及仿真时间

(1)液体体积

测量点p1处压强情况如图6(a)所示。液体体积越大(液面高度越高)，压强越大，当h=0.05 m时，该测量点处存在周期性不受压时段。对于5种不同液面高度，压强曲线基本表现为“双波峰”形态。测量点p2处压强情况如图6(b)所示。5种不同液面高度工况在该测量点处压强值排序与测量点p1处压强值排序相同，当h=0.05 m,0.075 m时，该测量点处存在周期性不受压时段。随着液面高度的降低，压强曲线逐渐由“前波峰”加“后平台”形态过度为“单波峰”形态。测量点p3处压强情况如图6(c)所示。5种不同液面高度工况在该测量点处压强值排序与测量点p1,p2处压强值排序相同，当h=0.05 m,0.075 m,0.1 m,0.125 m时，该测量点处存在周期性不受压时段。对于5种不同液面高度，压强曲线基本表现为“单波峰”形态。测量点p4处压强情况如图6(d)所示。5种不同液面高度工况在该测量点处压强值排序与测量点p1,p2,p3处压强值排序相同，且全部存在周期性不受压时段。对于5种不同液面高度，压强曲线同样表现为“单波峰”形态。

贮箱y轴方向受力情况如图7(a)所示。5种不同液面高度工况均存在受力方向周期性改变现象(力值为正表示力方向沿y轴正向，力值为负表示力方向沿y轴负向)。随着液面高度的增加，y轴方向受力增大。5种不同液面高度工况y轴正负方向受力峰值均基本相同，受力曲线均表现为周期性均匀变化，无力震荡情况。

图6 不同液体体积测量点压强Fig.6 Pressure of measuring point of different liquid volume

续图6Fig.6 Continued

贮箱z轴方向受力情况如图7(b)所示。不存在受力方向改变情况，受力方向保持为z轴负向。随着液面高度的增加，z轴方向受力增大。5种不同液面高度工况受力曲线均表现为周期性均匀变化，无力震荡情况。

通过对不同液面高度工况下贮箱受力及压强情况仿真结果的描述可以作出如下分析：5种不同液面高度工况的根本区别在于液体的质量不同，液面高度越高，液体质量越大。而正是这个原因，导致了贮箱受力及压强表现出仿真结果展示的规律和现象。不同测点位置的压强区别与贮箱在y,z两轴受力方向上的不同则体现出与正弦、阶跃运动模式下的仿真结果相同的规律。不同液体体积晃动情况如图8所示。

(2)挡板设置

测量点p1处压强情况如图9(a)所示。无挡板工况压强最大，hp=0.05 m工况压强最小，其他3种工况压强值由大到小依次为：hp=0 m，hp=0.025 m，hp=0.075 m。当hp=0.075 m时，压强曲线表现为“前波峰”加“后平台”形态；当hp=0.05 m时，压强曲线表现为“单波峰”形态；另3种工况下压强曲线表现为“双波峰”形态。测量点p2处压强情况如图9(b)所示。hp=0 m工况压强最大，hp=0.05 m工况压强最小，其他3种工况压强值由大到小依次为：hp=0.025 m，无挡板，hp=0.075 m。当hp=0 m及hp=0.025 m时，压强曲线表现为“双波峰”形态；当hp=0.05 m时，压强曲线表现为“单波峰”形态；另2种工况下压强曲线表现为“前波峰”加“后平台”形态。测量点p3处压强情况如图9(c)所示。5种不同挡板设置在该测量点处压强值排序与测量点p1处压强值排序相同，压强曲线全部表现为“单波峰”形态，且全部存在周期性不受压时段。测量点p4处压强情况如图9(d)所示。5种不同挡板设置在该测量点处压强值排序与测量点p1,p3处压强值排序相同。hp=0.05 m及hp=0.075 m两工况在该测量点处仿真全程不受压，另三种工况压强曲线均表现为“单波峰”形态。

图7 不同液体体积贮箱受力Fig.7 Tank force of different liquid volume

图8 不同液体体积晃动情况Fig.8 Sloshing state of different liquid volume

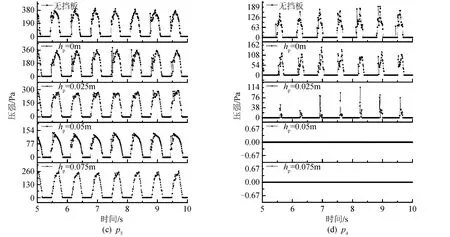
图9 不同挡板设置测量点压强Fig.9 Pressure of measuring point of different baffle position

贮箱y轴方向受力情况如图10(a)所示。5种不同挡板设置均存在受力方向周期性改变现象(力值为正表示力方向沿y轴正向，力值为负表示力方向沿y轴负向)。无挡板工况受力最大，hp=0.05 m工况受力最小，其他3种工况受力值由大到小依次为：hp=0 m，hp=0.025 m，hp=0.075 m。5种不同挡板设置y轴正负方向受力峰值均基本相同，受力曲线均表现为周期性均匀变化，无力震荡情况。贮箱z轴方向受力情况如图10(b)所示。不存在受力方向改变情况，受力方向保持为z轴负向。5种不同挡板设置在z轴方向受力值排序与在y轴方向受力值排序相同。5种不同挡板设置受力曲线均表现为周期性均匀变化，无力震荡情况。

通过对不同挡板设置工况下贮箱受力及压强情况仿真结果的描述可以作出如下分析：设置挡板的目的在于抑制晃动，4种含有挡板的工况基本起到了抑制晃动的效果。在测量点p2处，hp=0 m及hp=0.025 m工况的压强都略大于无挡板工况，与期望效果正相反。这种增强晃动的现象仅发生于该测量点处的压强情况，说明是一种特例，而原因在于挡板的存在会改变液体的流动方式，致使贮箱部分区域受到的压强增大。抑制效果最好的工况为hp=0.05 m，这与参数设置存在一定关系，液面高度设置为h=0.1 m，挡板高度设置为hb=0.05 m，所以当挡板位置设置为hp=0.05 m时，贮箱内液体被分割为两个相对独立的空间，液体在其间不能自由流动，从而获得了最好的抑制效果，导致了贮箱受力及压强表现出仿真结果展示的规律和现象。不同测点位置的压强区别与贮箱在y,z两轴受力方向上的不同则体现出与正弦、阶跃运动模式下的仿真结果相同的规律。不同挡板晃动情况如图11所示。

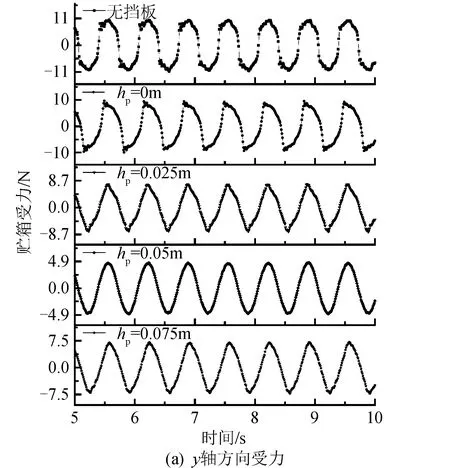
图10 不同挡板设置贮箱受力Fig.10 Tank force of different baffle position

图11 不同挡板晃动情况Fig.11 Sloshing state of different baffle position

3 结束语

由于晃动问题发生于航天器球形贮箱，贮箱的特殊形状使得液体极易发生强非线性晃动，传统网格类计算流体动力学方法及等效模型方法均无法描述这一现象,因此本文采用无网格类的SPH方法进行建模分析。首先掌握SPH方法的核近似、粒子近似原理，然后将该原理应用于流体介质控制方程(N-S方程)，得到离散近似的连续性方程、动量方程。在此基础上，通过选取核函数、拆分应力张量、处理边界问题、确定邻域粒子搜索方案等过程，最终建立基于SPH方法的流体动力学模型。通过对航天器球形贮箱不断变化的燃料含量及防晃挡板的设置方式等方面的分析与讨论，分别进行不同燃料液体体积及不同挡板安装位置仿真分析。记录仿真数据，分析贮箱受力及局部压强，仿真结果表明：运动加速度越大、变化越突然，贮箱受力及压强均越大、越易发生震荡。液体体积越大，贮箱受力及压强均越大。针对本文所建立的球形贮箱模型，设置挡板均会抑制液体的晃动行为，但在hp=0.05 m工况下，抑制效果最好。