最小数据丢失量的地月中继卫星任务调度研究
2020-04-10
1. 上海交通大学 区域光纤通信网与新型光通信系统国家重点实验室,上海 200240 2. 上海卫星工程研究所,上海 200240
全球新一轮的月球探索正在拉开序幕,探月范围正在逐步由月球正面向背面和两极拓展,探月活动也日趋复杂[1-4]。由于月球的自转周期和公转周期相同,地球地面站无法与月球背面直接通信,而借助地月中继卫星的中继通信方式可以解决这个问题,并满足面向月球的全时域、全空域覆盖的通信要求[3]。
地月中继卫星是指为月球表面的探测器、着陆器、环月卫星等提供数据中继和测控服务的通信卫星。地月中继卫星任务调度是指地面任务管理中心根据用户提出的服务申请,合理地分配地月中继卫星资源及执行时间,以尽可能地满足用户服务需求,提高地月中继卫星资源的利用率。随着人类对月球的探测不断深入[5],未来十几年各国发射的月面探测器也将不断增多。地月中继卫星数据传输未来也将呈现大容量、多用户以及多任务的特点。但是地月中继卫星的资源是极其有限的,如何利用有限的地月中继卫星资源,完成更多的任务并获得更好的收益将显得越来越重要。
近年来,近地的中继卫星任务调度问题已经有很多人研究[6-9]。Rojanasoonthon等[10]采用并行机调度理论研究了美国TDRSS系统调度问题,考虑了任务的优先级,建立了混合整数规划模型,以最大化任务完成数量为目标,采用贪婪随机搜索算法对其求解。文献[11]考虑到了数据中继卫星激光和微波混合链路系统的资源和任务的约束,建立了混合链路资源调度模型,以最大化完成任务优先级之和为目标,提出了一种基于改进的遗传算法。文献[12]提出了中继卫星日常任务的调度模型,也是以最大化完成任务优先级之和为目标,采用人工蜂群算法求解。文献[13]针对中继卫星任务的动态性,以最大化完成任务优先级之和以及最小化任务重调度数量为目标提出了一种两阶段任务调度算法。
上述基于近地中继卫星的任务调度研究通常都是以最大化完成任务数量和最大完成任务优先级之和作为其优化目标,一般考虑任务的优先级、用户卫星与中继卫星的可见时间窗口约束以及卫星天线资源的约束。这些研究对于数传任务很少考虑用户的存储限制,数传任务在规定截止时间内传输完成,一般就认为任务完成。但是在现实情况下,用户由于与地月中继卫星不可见或者中继卫星资源被占用等原因,产生的数据不能马上进行传输,需要放入存储器中等待一定时间。在等待与中继卫星进行数据传输的时间内,用户也将不断产生数据,新产生的数据也将会放入存储器中,等待传输。那么如果用户的剩余存储容量不足以支撑用户的下一次任务所需存储容量,那么下一次任务数据将丢失(或者新产生的数据覆盖原来的旧数据,还未传输的旧数据丢失)。而在月球探测过程中的数据和图像是非常珍贵的,在完成任务收集到数据时,期望这些数据能尽可能多的传输到地面,尽可能减少数据的丢失量。
地月中继卫星的任务包括实时性任务(如遥控遥测类任务)和延迟容忍类任务(如数传类任务)。本文针对地月中继卫星的延迟容忍类任务,即数传任务展开研究,研究目标是尽可能使数传任务的数据丢失量最小,从而提高地月中继卫星资源的利用率。
1 地月中继卫星任务调度模型
1.1 问题描述
地月中继系统如图1所示,地月中继系统由地月中继卫星、用户和地面站3部分组成。未来地月中继卫星将有以下几类用户:环月卫星、月球探测车、着陆器、月表栖息地、宇航员等。未来地月中继卫星系统中传输的任务将包括遥控、遥测、数传、话音、视频、导航等类型[3],其中只有数传任务是延迟容忍类业务,其余为实时性任务。本文的研究问题是如何合理的安排这些数传任务的执行时间,减少数据的丢失,提高中继卫星的资源利用率。
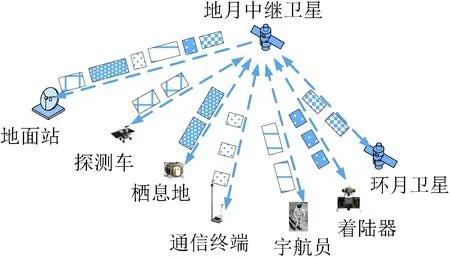
图1 地月中继系统模型Fig.1 Model of Earth-Moon relay system
随着探月的深入,月球上的用户数将会不断增多,任务将会随之增多。但是地月中继卫星在同一时间能服务的用户数量是有限的,并不能满足所有用户的要求。所以本文的目的是在满足地月中继卫星任务调度约束的前提下,找到一种合适地月中继卫星资源调度策略,使得数传任务的数据丢失量最小。
为了简化研究问题,假设:
1)由于实时性任务的优先级相对于数传任务的优先级较高,所以在本文中对于数传任务的研究是在实时任务调度完成之后,所用的时间窗是地月中继卫星的剩余时间窗口资源。
2)所有数传任务的任务开始时间是已知的,是静态的任务调度研究。静态业务是指任务提前可预知,在任务开始之前有足够的时间进行任务规划,可以采用耗时较长的搜索算法来寻求优化解。数传任务的结束时间是仿真结束时间,任务在仿真结束时间之前回传即可,存储溢出就算任务调度失败。
3)不考虑数据采集阶段的消耗时间。假设数据在数传任务开始时存储到用户中。数传任务执行结束后,会释放数传任务的存储空间。
4)不考虑中继卫星从一个用户切换到另一个用户所需要的时间。
地月中继卫星任务调度的约束包括以下几点。
(1)地月中继卫星用户属性约束
地月中继卫星用户属性约束包括可见时间窗约束和用户存储约束。
可见时间窗约束:用户与地月中继卫星并非时时可见,只有当他们位于彼此可见的范围内,才能建立通信链路,所以任务的执行时间必须在中继卫星与用户的可见时间窗口内。
用户存储约束:针对于数传任务来说,用户的剩余存储容量必须大于任务所需存储量,任务才能正常执行,否则直接判定任务调度失败。用户的剩余存储容量对于每一个任务来说可能都是不一样的,需要根据这个任务之前开始的任务的调度状态来确定。
(2)任务属性约束
用户提交任务申请时,会提交任务的优先级、任务的持续时间、任务最早开始时间以及任务最晚结束时间。对于数据传输类任务除了上述要求外,还需要知道任务的数据量大小,及用户的剩余存储量。
进行任务调度时必须考虑以下内容:1)任务的执行时间必须在任务的有效时间内;2)任务一次传输完成,不考虑任务拆分;3)对于新产生的数据传输类任务要考虑用户剩余存储容量是否超出任务的数据量。若任务的数据量超出用户的剩余存储容量,则该任务数据被丢弃。
(3)中继卫星资源约束
地月中继卫星资源在本文中指地月中继卫星数目以及一颗地月中继卫星在同一时刻能连接的用户数量。
1.2 符号说明
数学模型中出现的相关符号说明如下。
U:用户集合,用户数目为Nu。
Tu:用户u的任务集,任务总数是Nt。
qi:任务i的数据量大小,i∈Tu。
[tsi,tei]:任务i的有效时间,tsi为任务i的最早开始时间,tei为任务i的最晚截止时间。
di:任务i的持续时间,i∈Tu。
Si:用户u在将要开始执行任务i时的剩余存储容量。
M:地月中继卫星的链路集合,数量为Nm。
Vj:表示链路j的数据传输速率,所以任务i在链路j的持续时间di=qi/Vj。
Wij:任务i在链路j上的时间窗口集合,时间窗口数量为Nw。
Wsij(k):任务i在链路j上的第k个时间窗口的开始时间。
Weij(k):任务i在链路j上的第k个时间窗口的结束时间。
yij(k):表示任务i在链路j上的第k个时间窗口上的调度情况,yij(k)∈{0,1},yij(k)=0,则表示任务i在链路j上的第k个时间窗口上调度成功,反之,则任务失败。
τsij:任务i在链路j的开始执行时间。
τeij:任务i在链路j的执行结束时间。
1.3 数学模型的建立
基于上述的问题描述与分析,地月中继卫星任务调度问题的数学模型如下:
(1)
s.t.
τeij(k)=τsij(k)+di,ifyij(k)=0
(2)
(3)
qi≤Si,ifyij(k)=0
(4)
(5)
(6)
其中,目标函数f表示最小化数据丢失量。约束条件式(2)表示任务的结束时间是任务开始时间和任务持续时间之和。约束条件式(3)表示时间窗口的约束,任务的执行时间必须在可见时间窗口内,而且任务执行时间还必须得在任务有效期限内。约束条件式(4)表示,在开始任务i之前,必须确保用户的剩余存储容量大于任务i的数据量,否则任务i无法执行,这里的用户剩余存储容量是随着任务调度情况不断变化的。约束条件式(5)表示用户在同一时间只能通过一条链路执行任务。约束条件(6)表示地月中继卫星的一条链路在同一时刻只能服务于一个用户。
根据上述地月中继卫星任务调度模型,本文把任务调度转化为任务调度次序的求解。根据任务调度的顺序依次判断任务是否符合式(2)~(6),若是符合则任务调度成功,若是不符合则任务调度失败。所以目标是找到一个合适的调度顺序,使得任务的数据丢失量最小。一颗近地中继卫星的任务调度问题在文献[10]中已经被证明为一个NP-hard问题,所以在任务数量过大时很难在多项式时间求解。而通常求解这类问题会采用启发式算法和智能搜索算法。由于在本文中讨论的是静态业务调度,对于计算时间要求相对较小,所以为了得到更好的调度方案,采用智能搜索算法。
而烟花算法是一种新型的智能搜索算法,目前在很多领域取得比较好的应用。烟花算法通过爆炸的操作实现了局部搜索和全局搜索的平衡,相比于遗传算法,不容易陷入局部最优解,能找到更好的解。所以本文采用了基于离散烟花算法进行地月中继卫星任务调度的算法设计。
2 任务调度算法
2.1 烟花算法概述
烟花算法(Fireworks Algorithm, FWA)是根据烟花爆炸这种现象演变而来的一种群体智能搜索算法,自提出以来在很多领域得到了广泛的应用与研究[14-16]。
烟花算法由4部分组成:爆炸算子、高斯变异算子、映射规则和选择策略。爆炸算子的作用是在烟花周围产生火花,火花的数量和爆炸的振幅都是由爆炸算子决定的。然后通过突变算子产生一些火花。在经过两种算子后,如果新产生的一些火花不在可行解范围内,那么映射规则将这些火花映射到可行解区域内。最后用选择算子从火花中挑选出进入下一代的群体。烟花算法将不断执行上述的过程,直到符合终止条件。
传统的烟花算法是为了实参优化而设计的,其中的爆炸算子和变异算子适合用在较大的空间中搜索,然后通过选择算子决定下一代烟花种群。但是地月中继卫星任务调度问题则是一个组合优化问题,是离散数学问题,所以不能把标准的烟花算法直接应用到求解地月中继卫星任务调度问题中。针对求解地月中继卫星任务调度问题,本文设计了一种求解地月中继卫星任务调度问题的离散烟花算法。该算法包含编码、任务调度算子、爆炸算子、变异算子和选择策略几部分。
2.2 编码
本文的离散烟花算法采用整数编码,一个烟花的位置定义为任务调度顺序的序列X={x1,x2,x3,…,xNtotal},其中xi是0~Ntotal中的一个整数,是任务的序号,其中Ntotal=Nt×Nu,是总任务数量。例如,X={6,3,5,4,1,2}表示首先调度任务列表中的第6个任务,然后调度任务列表中的第3个任务,按顺序依次调度。
2.3 任务调度算子
任务调度算子的功能是通过请求的任务序列X来获得最终的任务调度结果。编码生成调度序列,任务调度算子生成调度计划。这个算子也是适应度计算的基础,根据任务调度结果来计算每一个烟花的适应度。任务调度算子包含以下几部分:用户剩余存储资源计算,任务安排,时间窗口更新。该算子的具体操作如图2所示。该算子根据任务序列X依次调度每一个任务xi,对于每一个任务xi执行下列操作:首先判断该任务是否满足用户的存储约束,若是不满足,则判定任务调度失败。若是满足则遍历时间窗口,找到一个最早可用的时间窗口,若是找到可用时间窗口,任务调度成功并更新中继卫星的时间窗口,若是未找到则判定任务失效。不断重复上述步骤,知道所有任务都调度完成,得到最终调度方案。

图2 任务调度算子流程Fig.2 Task scheduling operator flow chart
下面将具体介绍任务调度算子的各个部分。
(1)用户剩余存储资源计算
每个用户在开始执行每一个数据传输任务之前,会把产生的任务数据存放到用户的存储器上,然后等待传输,在数据产生到数据传输完成之前必须占用用户的存储资源,在传输完成后释放存储空间。所以在任务调度安排之前必须确保用户有剩余的存储空间来存储这个任务的数据,这样才能使数据顺利地下传到地面站。即任务调度必须满足约束公式(4)。
所以在安排任务i的执行时间窗口之前,应该遍历任务i所在用户l产生的所有数传任务。对该用户上的每个任务j(i,j∈Tu,且i≠j),都应进行如下操作:
1)判断任务j开始时间是否在任务i开始之前,若是则继续下面操作。
2)判断任务j是否已经调度完成,若未调度,则跳转到步骤5)。若是调度完成则继续下面操作。
3)判断任务j是否调度失败,若调度成功则继续下面操作。
4)判断任务j的调度完成时间是否在任务i开始之前,若不是则继续下面操作。
5)从用户剩余存储中减去任务j的数据量大小。
最终输出对于任务i的用户剩余存储容量。
(2)任务安排
这一步操作主要遵循约束公式(2)和约束公式(3)。本文按照任务序列X中任务的调度顺序依次安排任务。对于每一个任务的时间安排,本文采取贪婪启发式规则,把每个任务安排到最早可用时间窗口。这样安排是为了更加充分地利用有限的中继卫星资源,使得任务安排更加的紧凑。
这里的可用窗口要满足下列条件:1)时间窗口是指中继卫星的剩余可用时间窗与用户和中继卫星的可见时间窗口的交集;2)而最早可用是指选择一个能够满足任务传输的最早的时间窗口。
(3)时间窗口更新机制
由于地月中继卫星的一条链路在同一时刻只能服务于一个用户,为了满足约束公式(6),本文采用了时间窗口资源删除更新的机制。这里的时间窗口是中继卫星的剩余时间资源,在每次任务成功调度后,把该任务所占用的时间窗口从中继卫星的可用时间窗口中删除。根据上述的任务安排方案,地月中继卫星时间窗的删除只可能是下列3种情形,具体的操作情况如图3所示。

图3 地月中继卫星可用时间窗口删除方法Fig.3 Method for deleting available time window
2.4 爆炸算子
对于烟花X首先按照式(7)计算出火花的个数L。
(7)
式中:L为烟花产生的爆炸火花个数;m为一个常量代表,表示所有烟花产生的爆炸火花的总数;Ymax为N个烟花中适应度最差的值;f(X)为烟花适应度;ε为一个极小的常数,在式中的作用是防止分母为零。
为了防止产生的爆炸火花过多或者过少,通过如下公式来对控制每个烟花爆炸火花的数量:
(8)
式中:a,b为0~1之间的常数,且a 再通过式(7)(8)计算出烟花X的火花个数L,然后按照下面的步骤得到L个火花: 1)随机选取序列X中的两个节点,然后反转这两个节点及其中间部分的序列,得到新的调度序列X′,图4所示为该爆炸算子的操作方法(以编号1~10的10个任务为例)。 图4 爆炸算子操作示意Fig.4 Explosion operator operation 2)计算得到的新的调度序列X′的适应度f(X′),把新序列的适应度与原序列的适应度f(X)进行比较,若f(X′) 对于烟花X,随机选取其中的两位,然后进行位置交换,若交换后的适应度f(X′) 从烟花、爆炸火花、变异火花一起组成候选集,选出N个烟花组成下一代的烟花种群。选择策略基于两个准则:1)采用精英保留策略保留最优烟花的个体;2)采用轮盘赌的方法选择剩余的N-1个烟花,烟花Xj被选择的概率为: (9) 式中:fmax为候选集中适应度最差的值;f(Xj)为烟花Xj的适应度。从式(9)可以看出,适应度越好的烟花,越有可能进入下一代中。 基于离散烟花算法的地月中继卫星任务调度的算法的总体思路如图5所示,这个算法的主要步骤如下: 1)在初始化阶段,输入任务信息,用户信息,中继卫星的可用资源信息等,确定种群规模N、爆炸火花个数Ne、变异火花个数Nm、控制劣解接受的参数θ、最大迭代次数Cmax,随机初始化N个烟花种群,并利用任务调度算子计算每个烟花的适应度。 2)判断迭代是否终止,若是没达到终止条件则进入搜索阶段。 3)通过爆炸算子和变异算子产生火花,计算所有火花的适应度,并和烟花一起放入选择算子中,选择进入下一代的个体。 4)重复步骤2)和3),直到最大迭代次数Cmax,最后输出最终的结果。 图5 基于离散烟花算法的地月中继卫星任务调度算法流程Fig.5 Lunar relay satellite task scheduling algorithm based on discrete fireworks algorithm 本文试验参考鹊桥号中继卫星为月球背面的嫦娥四号与玉兔二号探测器提供中继服务的场景。仿真时间为一天00:00:00-23:59:59,一颗地月中继卫星采用地月拉格朗日L2点的Halo轨道参数,这个中继卫星有3个信道用于数传任务。6个数传任务用户其中2个是环月卫星,其轨道参数如表1所示,另外4个用户是月球背面探测器。用户与地球中继卫星的可见时间窗口由STK导出。本文在MatlabR2016b平台上进行仿真试验。 表1 环月卫星的轨道参数 在仿真试验时,首先对60个实时任务进行调度,然后获得地月中继卫星的剩余可用时间窗。再利用离散烟花算法对数传任务进行调度。 仿真中各参数设定如下:数传任务的开始时间在一天内随机分布,数传任务的结束时间没有进行设置,只要在数据丢失之前回传即可;数传任务的数据量是100~400 Gbit之间的随机值;每条链路的传输速率为100 Mbit/s;任务的传输时间由任务的数据量和信道的传输速率所决定;6个用户的剩余存储空间在200~800 Gbit之间随机选择。 为了验证算法的性能,分别采用本文的算法(DFWA)和遗传算法(Genetic Algorithm,GA)进行仿真验证。遗传算法的种群数量为20,遗传概率为0.8,变异概率为0.1,迭代次数为100次。烟花算法的参数设置如表2所示。 表2 参数设置 在任务数量为42时,两种算法的调度结果甘特图如图6所示。其中彩色部分是数传任务,空白的矩形块是中继卫星在进行数传任务调度时已经被占用的资源。在这种情况下,基于DFWA的算法的任务安排数量为39,数据丢失量为609 Gbit。而遗传算法的任务完成数量为35,数据丢失量为1683 Gbit。可以看出,基于DFWA的算法在求解结果上要优于遗传算法。图7是两个算法在任务数量为42的一次试验的搜索过程,从图中可以看出,基于DFWA的算法的在搜索最优解方面有更好的特性。 图6 任务数量为42时的算法调度结果示意Fig.6 Algorithm scheduling results when the task number is 42 图7 任务数量为42时智能算法的搜索过程Fig.7 The search process of intelligent algorithm when the task number is 42 两个算法的运行时间上,基于离散烟花算法的运行时间要比遗传算法时间长0.25倍。遗传算法的时间复杂度是O[Cmax×(N+Nc+Nm)×K],其中Cmax是迭代次数,N是种群数量,Nc是交叉产生的种群数量,Nm是变异的种群数量,K是适应度计算的时间复杂度。烟花算法的时间复杂度是O[Cmax×(N×L+Nm)×K]。其中Cmax是迭代次数,N是种群数量,L爆炸火花个数,Nm是变异的种群数量,K是适应度计算的时间复杂度。这两个时间复杂度的区别主要在于子代的数量。遗传算法的子代依赖于遗传和变异的概率,相对于烟花算法来说产生的子代数量较少,所以遗传算法的复杂度相对要低一些。但是烟花算法由于其爆炸和变异的特性,在搜索最优解的时候不容易陷入局部最优,所以其求解效果要更好一些,能求得更好的解。所以可以说,基于烟花算法的地月中继卫星任务调度的算法是牺牲了部分的运行时间来得到一个更好的解。由于本文考虑的是静态任务调度,即业务提前一定时间到达。根据NASA 发布的中继卫星系统用户使用手册:中继系统以一周为周期,对业务进行资源分配。所以对于静态业务调度问题来说,算法的运行时间长短影响并不是很大。 为了进一步验证算法的有效性,本文还比较了任务规模数量为30、60、90、120、150的情况。在这些任务规模数量下,分别采用遗传算法和基于离散烟花算法的地月中继卫星任务调度算法进行仿真计算,把算法运行20次,最终结果取平均值。为防止任务属性的不同对算法造成影响,试验时每次任务都是随机产生的。两个算法的运算结果如图8所示。由图8可知,虽然在任务数量比较少的时候两个算法求得的解没有很大差别,这是由于任务数量较少,资源比较充足的原因。但是当任务数量比较多的时候,基于DFWA的算法求解能力总是优于遗传算法。 图8 不同任务规模下的算法对比Fig.8 Comparison of algorithms under different task sizes 本文首次根据地月中继卫星任务调度问题的特点,综合考虑了中继卫星资源约束,任务属性约束和用户的存储约束,以最小化数据丢失量为目标,建立了地月中继卫星任务调度的约束满足模型,并基于该模型提出了一种基于离散烟花算法的地月中继卫星任务调度算法。根据仿真结果可知,相比于遗传算法,该算法能有效减少数据的丢失。日后随着探月的不断发展,任务类型也将趋向于多元化,任务的动态性也将会增加,而且地月中继卫星也将可能会形成一个卫星网络,这将是未来研究的重点。另外,本篇文章为了简化问题做了较多假设,对于地月中继卫星资源调度模型还有很多不足,未来可以根据实际的情况对模型和仿真参数进行更具体的细化和研究。
2.5 变异算子
2.6 选择策略
2.7 算法的总体思路
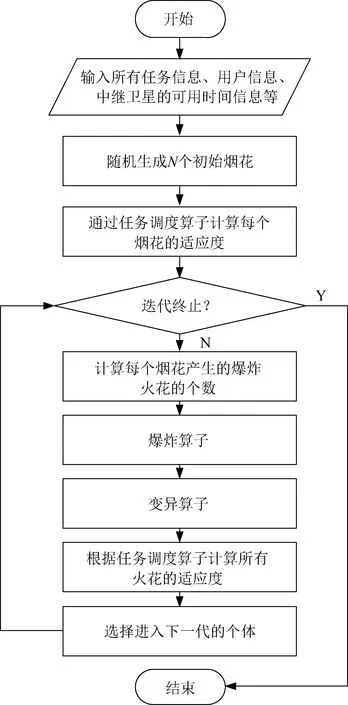
3 仿真结果及分析
3.1 仿真场景

3.2 仿真结果





4 结束语
