一种新型的用于深空高动态微弱信号载波跟踪环
2020-04-10
北京航空航天大学 电子信息工程学院, 北京 100191
由于深空通信的距离远,通信目标运动速度快,接收信号具有极低的载噪比和较高的多普勒动态[1], 载波跟踪是信号接收的重难点问题。传统二阶锁频环辅助三阶锁相环[2](FLL-PLL)环路带宽固定,因此方法在深空通信环境中受到限制。为此现代学者提出两种方法:
1)根据载波跟踪结果实时控制环路滤波器参数,达到变带宽目的[3]。其优点是易于实现,多应用于近距离卫星通信,导航接收机当中。但其本质仍是低信噪高动态的折中选择,无法同时满足二者需求。
2)使用现代滤波方法。区别于传统滤波方法,现代滤波本质上使用数学统计规律对状态量进行某种条件下的最优估计,例如传统卡尔曼滤波(KF)[4]、扩展卡尔曼滤波(EKF)[5],也有少量探讨了无迹卡尔曼滤波(UKF)[6]、容积卡尔曼滤波(CKF)在跟踪环路中的应用。但鲜有学者从众多滤波方法的原理上进行对比分析。
本文从理论上分析了这些方法并在此基础上提出了新型载波环路,通过计算判别结构控制环路输出,同时完成了野值剔除功能。
1 载波跟踪环路结构
设载波跟踪环路中的输入信号为BPSK调制信号:
s(n)=Ab(n)cos (ωinTs+θi)
(1)
式中:A为信号幅度;b(n)为信息比特;Ts为采样间隔;ωi和θi分别为输入信号的中频频率和初始相位。 输入信号与本地数控振荡器(NCO)复现频率相乘后滤除高频分量,经T=NTs时间的相干积分,可得两路正交信号:
(2)
(3)
式中:Δω和Δθ分别为输入信号与NCO的频率、相位差;tk-1为前一积分时刻。
在载波跟踪中使用锁频环是必要的,目的是更快地进行频率牵引,为后续环路尤其是迭代滤波提供有效的状态初值,常用自动频率牵引(AFC)算法[7]。点积Pdot,叉积Pcross的定义如下:
Pdot=I(k-1)I(k)+Q(k-1)Q(k)
(4)
Pcross=I(k-1)Q(k)-Q(k-1)I(k)
(5)
利用四象限反正切函数可得鉴频,鉴相误差:
Δω=arctan 2(Pcross/Pdot)/T
(6)
Δθ=arctan [(Q(k)/I(k)]
(7)
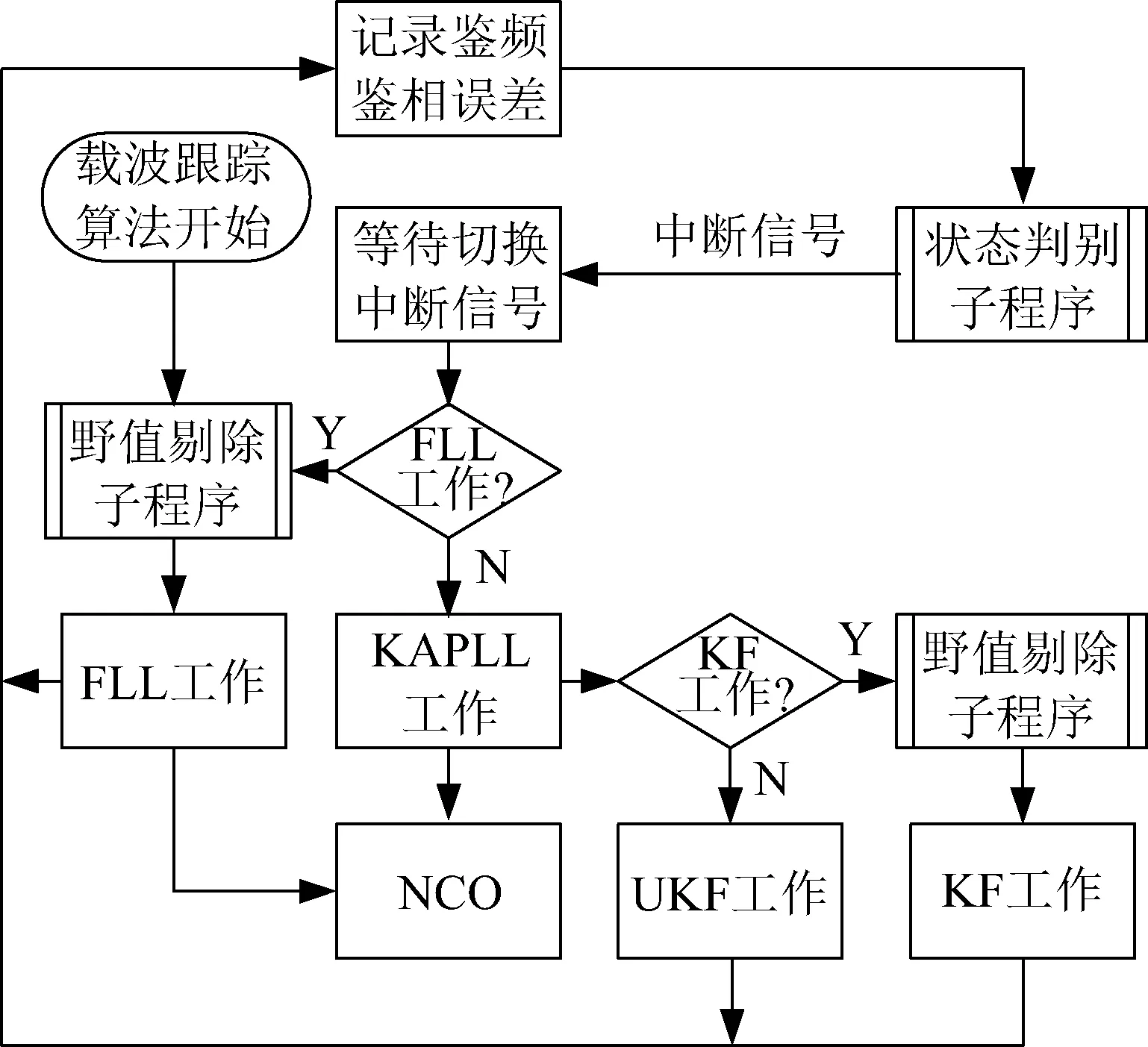
本文提出的新型载波环路如图1所示,在通常的低信噪比高动态环境下,使用强跟踪KF算法进行跟踪,KF算法解决了动态性和跟踪精度的矛盾问题,强跟踪算法在一定程度上修正了算法模型的不准确,增强算法的鲁棒性。而在更低的信噪比下使用非线性滤波即强跟踪UKF算法。FLL为环路提供初牵引。三者的切换由计算判别结构控制,该结构控制着环路输出,使开关平滑,提高了精度,同时在不浪费计算力的情况下剔除野值,加快了环路收敛速度,增强了环路稳定性。

图1 载波跟踪环路结构Fig.1 Carrier tracking loop structure
2 滤波方法的分析与设计
2.1 滤波模型理论分析与选择
载波跟踪环路基本的非线性模型如下:
(8)
式中:xk和zk分别为第k时刻的状态向量和观测向量;h为量测方程;f为状态转移方程;W为高斯状态转移噪声向量,其协方差矩阵为Q;V为高斯观测噪声向量,其协方差为R。
(1)状态模型
显而易见宇航器的完整的非线性运动方程f未知,其概率分布密度也不可预测。因此最大似然估计、EKF、UKF、CKF、粒子滤波(PF)等非线性滤波方法皆无法对未知的非线性状态转移方程使用,为此只能近似化状态方程[8]。设在载波跟踪中的n维载波状态量为:
x=[Δθ,Δθ(1),Δθ(2),…,Δθ(n-1)]T
(9)
式中:Δθ为相位差;Δθ(1)为相位1阶导,即频率差Δω,相位n-1阶导Δθ(n-1)即频率Δω(速度信息)的n-2阶导。在T时间内做泰勒展开并舍弃n-1以后的高阶项有:
(10)
因为舍弃高阶项,最高项Δθ(n-1)无法随时间实时更新,默认Δθ(n-1)前后时刻不变,即:
(11)
式(10) (11)联立,有:
(12)
观察式(12),状态方程模型此时为线性,在两方面引入了误差:一是Δθ的等式舍弃了n-1阶后的高阶项,二是在n-1阶处,k时刻与k-1时刻前后相等。这意味着在极端条件下,如火星的进入下降和着陆(EDL)过程,宇航器运动变化极其剧烈,Δθ不再准确,Δθ(n-1)不能及时更新,有可能使环路发散。这是以有穷列举无穷所导致的必然。现给出如下推论。
推论1:在高信噪比及系统模型、噪声模型准确的情况下,状态量维数n决定了在高动态条件下的载波跟踪能力。图6佐证了这一点。现代滤波使用的一大掣肘即是量测方程固定,即式(12)框架上。
(2)量测模型
载波跟踪中量测方程与环路结构有关,当环路中存在鉴相器时,观测变量只有1维为鉴相结果θerr(T),在T内的平均鉴相结果有:
(13)
观察式(13),此时量测方程为线性。当环路不存在鉴相器时,直接观测I(k),Q(k)。由于Δω近似为0,有:

(14)
为去除数据位b(k)取±1的影响,通常使用平方法或比特翻转法[9],可统一表达为 :
(15)
式中:K1,K2为消除b(k)后的常系数,由于对称性一般二者相等;L1,L2为线性函数,考虑到式(14)的对称性,一般二者相等。此时的量测方程h(x)为非线性。鉴相计算是一种非线性计算(如乘法,反正切法),直接观测避免了鉴相引入的非线性噪声误差,同时较完整地直接地描述了含噪声的非线性量测方程,所以给出下面的推论。
推论2:非线性滤波的使用只针对量测方程的非线性,与状态方程的非线性无关。在相同状态模型、噪声模型下,量测方程的选择影响在低信噪比情况下的载波跟踪能力。
2.2 算法选择与具体设计
考虑到推论1,非线性滤波计算量大,KF方法在工程上已经得到较好的应用,本文在较高信噪比的情况下使用KF。在低信噪比时,考虑到UKF在计算量与准确性上较EKF优越,与UKF相比,CKF在低维时无明显优势,PF计算量巨大且存在粒子退化现象,本文在低信噪比的情况下使用UKF。
使用KF时代入方程(12)(13),在T内有状态转移方程与观测方程:
(16)
(17)

(18)


(19)
式中:n为矩阵维度,本文即4;α为比例缩放因子,决定了 sigma 点到均值的距离,取值范围在(10-4,1);k为第二比例系数,影响二阶以后的高阶矩带来的偏差,本文取0;β与状态先验分布有关,影响协方差精度,在高斯分布下β=2最优。

(20)
(21)
(22)
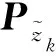
为增强算法鲁棒性,消除线性化状态方程及噪声模型不准确带来的误差,必须引入强跟踪算法(STF)。强跟踪算法的核心思想是利用KF的正交性原理[12],即:
(23)
式中:ηk为新息序列,理想情况下卡尔曼滤波新息序列正交;λk为渐消因子,嵌入一步预测误差协方差矩阵Pk/k-1,从而调整增益矩阵Kk,强迫新息正交[13]。
在KF中有:
(24)
Pk/k-1得到修正:
Pk/k-1=λkAPkAT+Qk-1
(25)
在UKF中有:
(26)
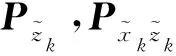
(27)
至此,卡尔曼滤波辅助的锁相环(KAPLL)算法构建完毕。
3 环路的3种工作模式与切换条件
设定FLL工作时为状态A,KF工作时为状态B,UKF工作状态为C。整个环路模式切换如2图所示。

图2 工作模式示意Fig.2 Working mode switching
本文提出的新型环路增加了一个计算判别模块控制3种模式转换,考虑到复杂度与环路锁定速度,该模块内的算法应尽量简单,以求和运算、条件判断为主,尽量避免出现乘法、指数运算及循环。计算判别模块有3大功能:存储,计算,判别。该模块存储FLL的鉴频输出与 KAPLL的鉴相输出。求出FLL与 KAPLL最近L,M个输出均值:
(28)
L是鉴频误差累加个数。
(29)
M是鉴相误差累加个数。本文仿真中,L,M都取20。K小于L,M时,不进行计算与判别。
3.1 工作状态切换
当
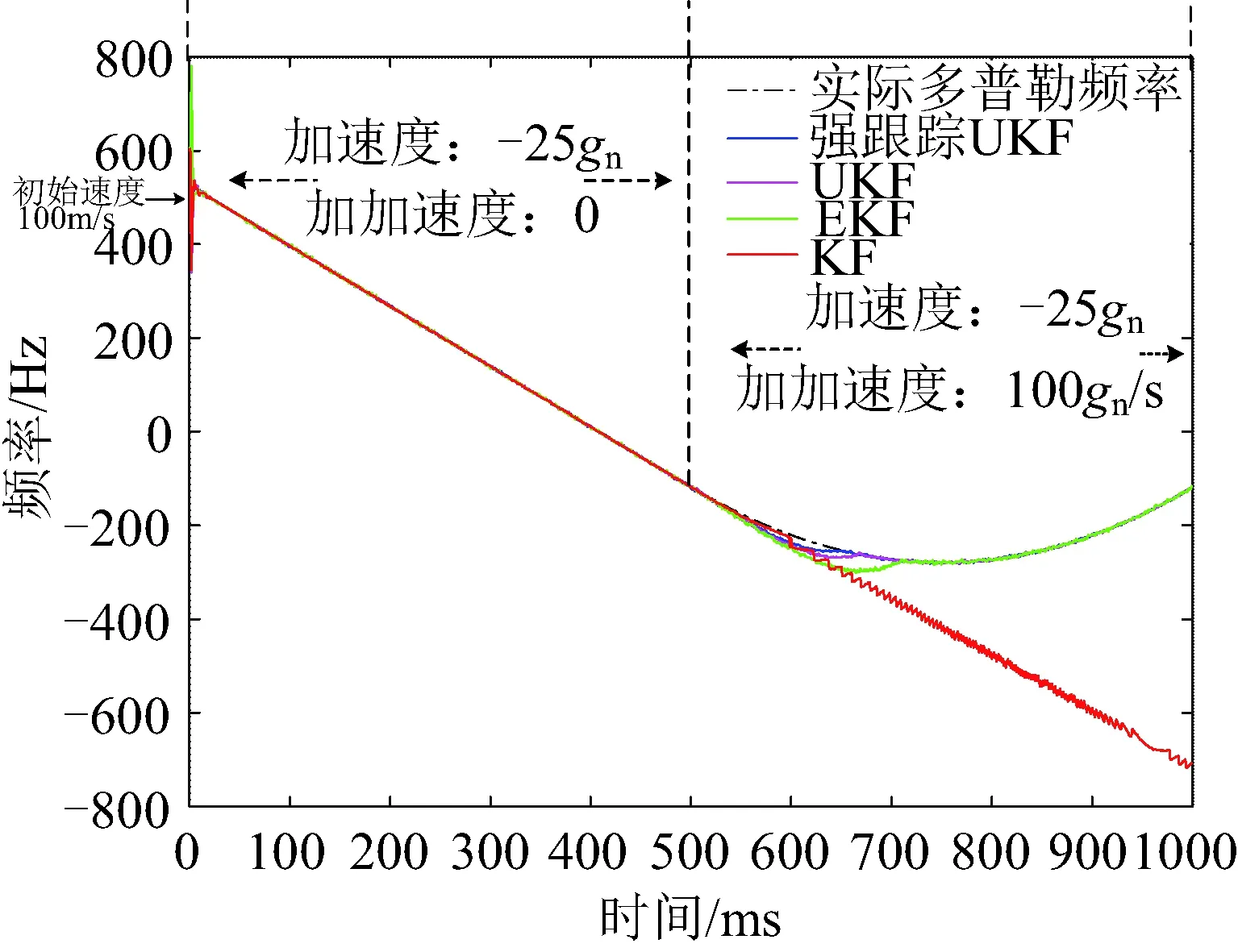
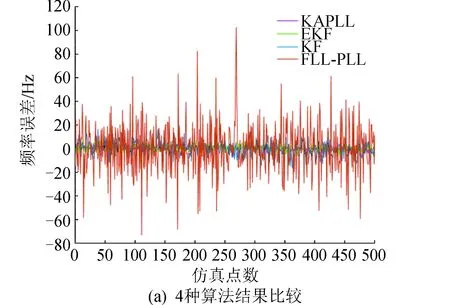
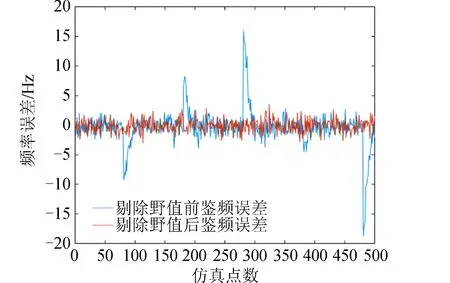
m(k) (30) 且 abs{[a·n(k)-m(k)]/m(k)} (31) 式中:P为阈值;a为NCO的相位-频率转换系数;p本文取20%。式(30) (31)目的是为了消除开关硬切换时的峰值,当m(k)与n(k)控制的NCO本地频率相差较近A向B或C转换。 当 n(k)>Q (32) 说明鉴相误差高于阈值Q,B或C向A切换。 UKF与KF迭代框架相同,都是以协方差矩阵调整增益矩阵的卡尔曼形式,因此B,C之间硬切换平滑,其切换门限由输入信号的载噪比CNR决定。CNR信息是卫星通信中的重要辅助信息,其工程应用成熟,一般在相干积分过程中即可完成估计,常用的方法是方差和方法(VSM)与功率比方法(PRM)[14]。 为了不浪费式(27) (28)的计算结果,可通过添加简单的判别,有效地剔除野值。若鉴频误差Δω(k)突然变得极大,是上一时刻FLL鉴频误差均值m(k-1)的q倍时,即可认定该值为野值,并修正为Δωnew(k),即 Δω(k)>q·m(k-1) (33) Δωnew(k)=m(k-1) (34) 需要注意的是,当上一时刻为修正值Δωnew(k-1)时,当前时刻鉴频误差Δω(k)禁止修正,以防错误蔓延。 野值剔除通常应用于FLL与KF当中,因为UKF中野值与失锁时的值较难区分。剔除野值的好处有两点,一是加快环路锁定速度,二是保证环路的稳定性。 综合前文所讨论计算判别器的功能,图3给出了其主程序算法流程。 图3 主程序算法流程Fig.3 Main program algorithm flow chart 载波频率为GPS的L1,f=1 575.42 MHz,中频频率不影响仿真,设信号中频为1 MHz采样频率为8 MHz,积分时间T为1 ms。传统3阶锁相环环路带宽取47 Hz,信号载噪比很低时取25 dB·Hz,高时取50 dB·Hz。根据美国喷气推进实验室(JPL) 设计的高动态模型[15],初始速度v=100 m/s,加速度为25gn,加加速度为100gn/s,可得多普勒频率,多普勒加速度,多普勒加加速度为: (35) 式中:gn=9.8 m/s2;c=299 792 458 m/s。 传统的3阶锁相环无法跟踪载噪比为25 dB·Hz的高动态模型。在500 ms处突然加入-25gn/s的加加速度。如图4所示,在四维状态模型下,加加速度无法实时精确跟踪,明显观察到KF已然发散,强跟踪UKF能最快回归收敛。 图4 低载噪比高动态信号载波跟踪曲线Fig.4 Low CNR high dynamic signal carrier tracking 为对比在低信噪比时的性能,令输入信号载噪比为25 dB·Hz,排除高动态的影响,跟踪目标只存在恒定速度。其跟踪频率误差如图5所示,图5(b)由图5(a)去除最差方法后得到,更加直观。可以得出,在低载噪比情况下,FLL-PLL明显最差,误差最高,KF次之,KAPLL与EKF明显较好,且KAPLL稍优于EKF。 图5 低载噪比信号载波跟踪误差Fig.5 Low CNR signal carrier tracking error 为对比算法在高动态时的跟踪性能,排除低信噪比的影响,令输入信号载噪比为50 dB·Hz,跟踪目标有加速度与恒定加加速度。其跟踪误差频率如图6所示,图6(b)由图6(a)去除最差方法得到,更加直观。可以得出,传统方法与FLL-PLL算法的鉴频误差随多普勒频移的增大而明显增大,其他3种算法在高载噪比时误差几乎相当,从侧面印证了推论1。 图6 高动态信号载波跟踪误差Fig.6 High dynamic signal carrier tracking error 图7表明了传统开关切换时的频率阶跃现象,以及本新型环路在模式切换上的改进。图8表明了野值的危害以及计算判别结构能够去除野值。 图7 频率阶跃现象的改善Fig.7 Improvement of frequency step phenomenon 图8 野值剔除前后对比Fig.8 Comparison before and after rejection of wild values 分析了滤波算法在跟踪环路中的作用,提出了两个推论,设计了新型载波跟踪环。 1) 算法可实现低载噪比下,满足JPL高动态模型(速度为100 m/s,加速度为25gn,加加速度为100gn/s)的载波跟踪。 2) 无论是低载噪比还是高动态信号,本文提出的FLL-KAPLL算法都明显优于传统方法,与其他新型算法相比亦占有优势。 3) 计算判别结构能够有效地消除开关切换时的频率阶跃现象,同时也能有效的剔除野值。 4) 关于本文提出的两个推论从滤波建模原理出发,对照了仿真结果定性得出的,并没有进行严格的数学推导与数学推论,这是笔者接下来要继续深化研究的方向。3.2 野值剔除
4 仿真校验




5 结束语
