基于球堆叠的月壤蓄热器传热特性数值研究
2020-04-10李蒙蒙胡定华李强
李蒙蒙,胡定华,李强
南京理工大学 能源与动力工程学院,南京 210094
载人深空探索已成为当前空间活动的焦点[1-2],世界各大国正在掀起一股新的深空探索热潮,月球已成为21世纪深空探索的主要目标。然而,在漫长的月夜(350 h),月球表面的温度可以低至-150℃,这给月球探测的能源供应构成了巨大的挑战。
美国Lewis研究中心的Colozza[3]在1991年就对月壤作为蓄热介质的可行性进行了分析,他们认为白天将太阳能储存至月壤,在夜间再转化为电能来为其他设备提供能量是一种较为可行的解决方案。美国波音公司的Tillotson[4]于1992年提出了通过压缩或融化月壤的方式来提高月壤的储热能力的方法,压缩月壤时可在月壤砖块间填充氦气来提高月壤的导热系数。NASA的Balasubramaniam[5]等建立了月壤储热模型,提出了通过月壤蓄热来在夜间为月球车保温的技术。而基于月壤蓄热的太阳能发电技术[6-11]作为一种月球资源原位利用技术是在月壤蓄热基础上的进一步探索,该技术能够在白天通过聚光器将太阳能储存至蓄热器,在夜间通过斯特林热机将热能转化为电能,从而实现在较长月夜持续为探月设备提供能量的目的。目前的研究仅限于月壤蓄热发电的概念和简单的理论计算,而月壤的堆叠形式和尺寸是影响蓄热效果的重要因素,因此针对影响蓄热效果的具体因素和机理还有待进一步的研究。
地面常见的物质堆叠蓄热试验和研究,较多以球堆叠多孔介质换热为对象。杨剑等[12-13]先后通过数值模拟和试验的方法对颗粒堆叠多孔介质的换热特性进行了研究,发现通过合理选择颗粒形状和堆叠方式可以提高综合换热效率。刘宏升等[14]建立了三维球形堆积床的随机结构模型,并使用数值模拟的方法研究了球形堆叠床随机结构内速度场特性和湍流参数的变化规律。Jiang等[15]用数值模拟的方法研究了非烧结的颗粒堆叠多孔介质的对流换热,并使用热平衡模型和非热平衡模型对试验工况进行了模拟,并得到了与试验一致的结论。然而在球堆叠多孔介质换热方面的研究仅有针对地面条件的相关试验,在如何实现针对月壤物性的球堆叠高温蓄热方面以及其传热特性方面还未见报道。
本文针对基于月壤的蓄热器开展数值模拟研究。蓄热介质采用普通月壤压制的球体,球体之间孔隙作为热介质流通的通道,罐体采用登月舱下降级推进系统的燃料罐。由于蓄热温度高且热介质直接和月壤接触,因此考虑使用较为稳定安全的氦气作为热介质[4]。在此基础上,建立了球堆叠多孔介质蓄热模型,模拟了氦气在蓄热器内的流动和传热过程,研究了月壤球的堆叠形式和直径大小对综合蓄热指数的影响,分析了不同堆叠形式对综合蓄热指数的影响机理,以及月壤球的最优直径和进出口压差的关系,从而对后续月壤蓄热器的设计提供理论依据。
1 蓄热模型及数值方法
1.1 几何模型
为降低发射成本,尽量减少航天器携带的载荷质量,在制造蓄热器时可考虑使用登月舱下降级推进系统的燃料罐作为蓄热器的外壳。燃料罐在下降完成之后结束使命,由于其容量大小合适以及保温性能良好,经过简单加工即可作为蓄热器的容器。本文以牵牛星号登月下降系统的燃料罐为研究对象[16]:该下降级具有4个氢气罐、4个氧气罐,罐体的体积见表1,通过不同罐体种类和数量的组合可以满足蓄热器不同容量的需求。本文采用其中2个氢气罐和1个氧气罐来组成蓄热器,罐体尺寸见图1。

表1 燃料罐体积

图1 燃料罐尺寸Fig.1 Fuel tank size
图2为月壤蓄热器和管道的布置示意图,蓄热器内部结构如图3所示。蓄热介质使用月球表层土壤,将月壤加工成直径大小合适的球体,再将其填充到燃料罐内。月昼时氦气被太阳能加热后从蓄热器罐口流入,从而不断加热月壤球,将热量储存在蓄热器中。进入月夜后,蓄热存储的热能可以通过热机转化为电能,或者直接使用来为其他设备提供热控保温功能。

图2 月壤蓄热器模型Fig.2 Thermal energy reservoir model of regolith
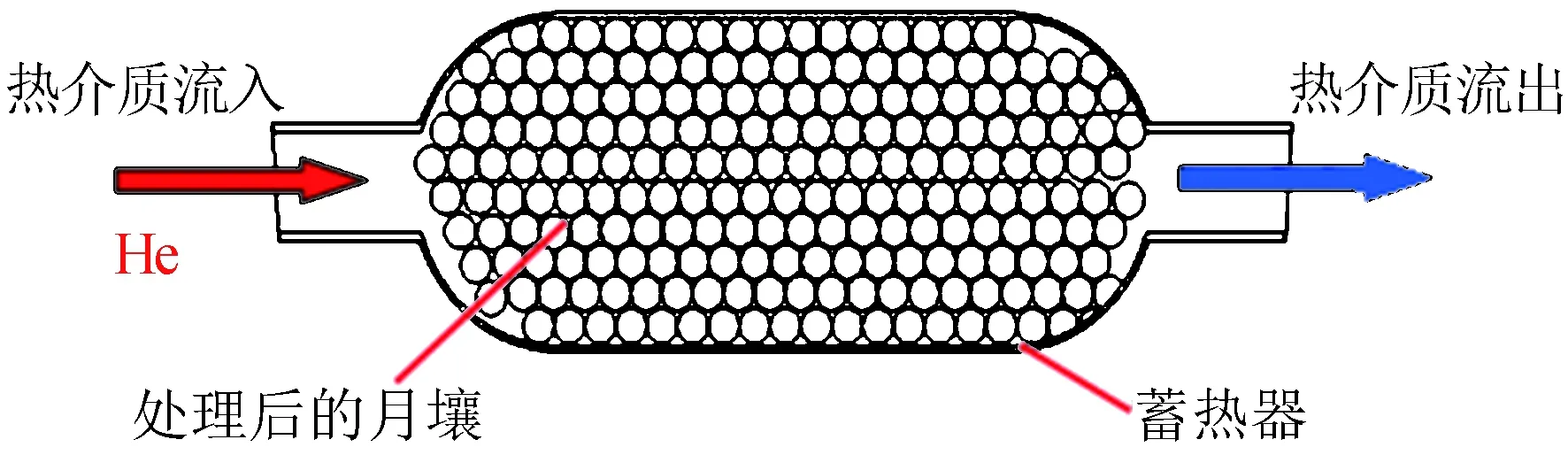
图3 蓄热罐内部示意Fig.3 Internal schematic of thermal energy reservoir tank
1.2 控制方程
如图3所示,加工后的圆球形月壤相对于燃料罐体积很小,堆叠在罐体中形成类似多孔介质结构,将不同的罐体分别填充满后,在罐体内形成多孔状区域。该区域中的流动传热过程可以采用多孔介质的传热流动模型来描述[17]:
(1)动量方程
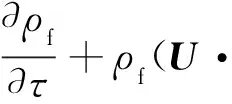
(1)

式中:dp为月壤球直径;P为压力;U为速度矢量;μ为动力学粘性系数;ρf为流体密度;ε为孔隙率;τ为时间。
(2)流体相能量方程
(2)
式中:Cf为流体比热容;hsf为对流换热系数;Ts,Tf分别为固体温度、流体温度;uf为流体速度;λf为流体导热系数。
(3)固体相能量方程
(3)
式中:λs为固体导热系数。
(4)连续方程

(4)
1.3 边界条件
蓄热器的几何结构和管道布置如图2所示,管道入口作为压力入口边界条件,保持进出口压差恒定来模拟泵提供的压力,本文分别模拟了200 Pa、1 000 Pa、5 000 Pa三种压力差。使用氦气作为加热介质,进口温度为1 000 K;蓄热器外围采用辐射隔热罩保温,计算中假定蓄热器外围为绝热状态;同时根据月球表面的最低环境温度,蓄热器的初始温度均设置为150 K。
1.4 月壤参数
在上述能量方程中(式(2)(3)),氦气与月壤球体的对流换热系数hsf的计算使用Kar[18]提出的换热关联式,该关联式适用于球形堆叠模型。
(5)
式中:Re为雷诺数;Pr为普朗特数。
原始月壤质地疏松,孔隙率大约为0.33,导热系数极低,只有0.012 W/(m·K),必须经过加工以提高其导热性能。考虑加压的方法见图4,将月壤在一定压力下压缩成球体,使孔隙率减小到0.1以下。假设孔隙率为0时月壤的导热系数与花岗岩相等(λ=2.46 W/(m·K)),再将孔隙内填充氦气(T=1 000 K时,λ=0.36 W/(m·K))。当氦气的压力足够高,氦气分子的平均自由程小于孔隙时,月壤的导热系数达到最佳[4]。
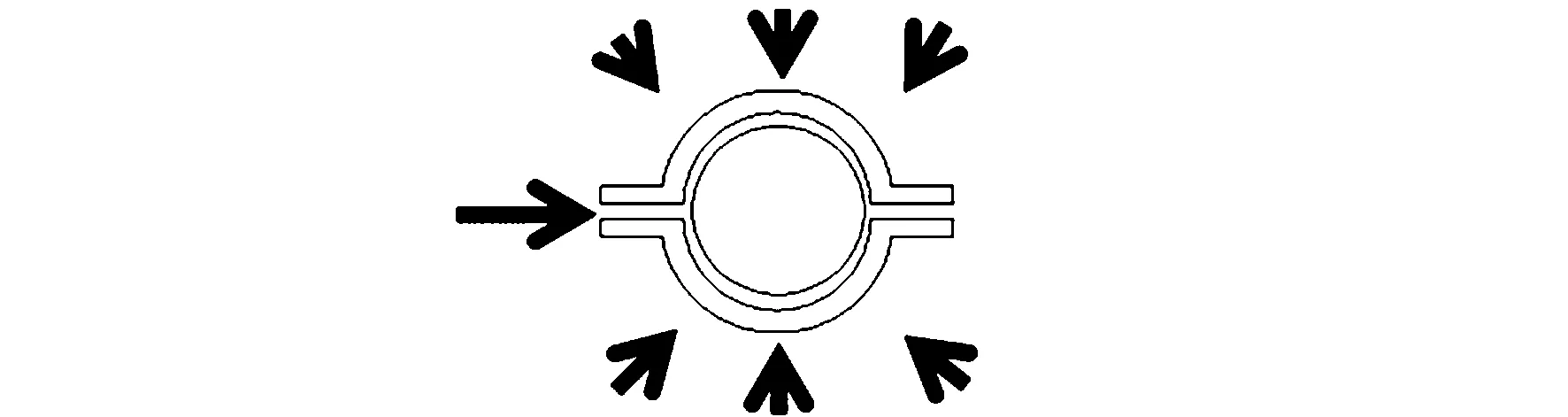
图4 月壤加工示意图Fig.4 Processing schematic of regolith
假设氦气和月壤颗粒之间为串联的传热方式,压缩后的月壤有效导热系数可用下式计算:
(6)
式中:λg为气体导热系数。孔隙率分别为0.33、0.1时串联有效导热系数为0.841 W/(m·K)、1.269 W/(m·K)。
假设氦气和月壤颗粒之间为并联的传热方式,压缩后的月壤有效导热系数可用下式计算:
λ=(1-ε)λs+ελg
(7)
孔隙率分别为0.33、0.1时并联有效导热系数为1.76 W/(m·K)、2.238 W/(m·K)。
根据原始月壤的参数以及压缩的加工方式,并考虑到氦气导热系数在1 000 K时的值比在初始温度150 K时偏大,因此处理后的月壤导热系数保守估计为1 W/(m·K),处理后的月壤参数估计如表2所示。
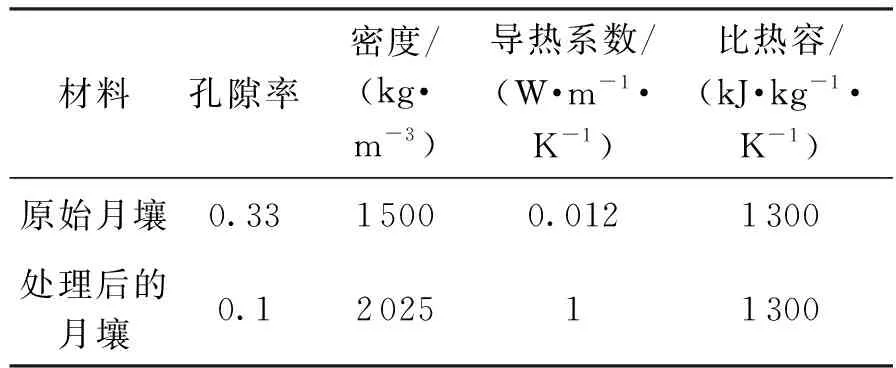
表2 月壤参数表[19]
1.5 数值方法
使用ANSYS中的Fluid Flow进行建模和求解,模型的网格划分如图5所示,采用Fluent的多孔介质模型和k-ε湍流模型。多孔介质模型使用非热平衡模型,使用SIMPLE算法隐式求解。网格独立性验证如表3所示,分别采用84659、122835和167862三种网格数量,可以看到采用122835和167862两种网格时,蓄热器的平均温升计算结果相对误差为0.1%。为了兼顾计算效率和计算精度,后续计算中将采用网格数122835来计算。

图5 网格划分Fig.5 Mesh generation

表3 网格数对蓄热器平均温升的影响
2 模拟结果及讨论
2.1 堆叠方式对蓄热效果的影响
图6给出了两种月壤球体在蓄热器中的堆叠方式示意图:简单立方体均匀堆叠(Simple Cubes,SC)和面中心立方体均匀堆叠(Face Centered Cubes,FCC)。两种堆叠方式的主要区别在于SC堆叠的球体均匀分布在立方体的八个顶点,FCC堆叠的球体分布在立方体的面中心以及八个顶点。由于FCC(ε=0.259)堆叠方式下月壤球体之间更加紧密,使得堆叠后的月球球堆的孔隙率要小于SC(ε=0.467)的堆叠方式。
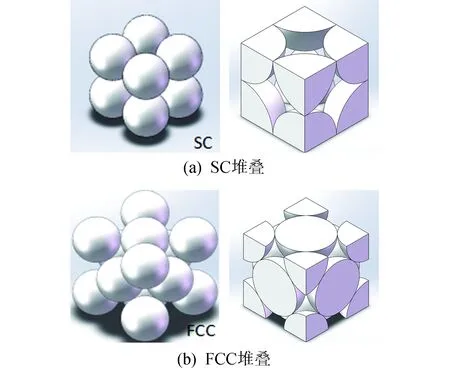
图6 简单立方体均匀堆叠(SC)和面中心立方体均匀堆叠(FCC)Fig.6 Simple cubes and face centered cubes


图7 月壤球直径为1cm时蓄热器温度分布Fig.7 Temperature distribution of thermal energy reservoir with 1 cm regolith ball diameter
图7给出了在SC和FCC两种堆叠方式下蓄热器的中心截面的温度分布,蓄热时间均为20 h,入口氦气压力为1 000 Pa,入口温度为1 000 K。由图可见,当使用1 cm直径月壤球在相同的蓄热时间下,两种堆叠方式的蓄热器出口温度接近初始温度,说明在20 h的蓄热时间下,氦气的热量均几乎被完全吸收。但可以显著看到,图中SC堆叠方式的蓄热器蓄热更快,这是由于SC堆叠阻力更小,在相同压力下SC堆叠球孔隙中的氦气流量更大,平均流量达到2.10 m3/s,因此其蓄热量更高,使得平均温升可达到625 K。而相同压力下FCC堆叠方式的平均流量为1.76 m3/s,导致其平均温升仅为286 K,前者蓄热量(由下式计算)为后者的1.56倍。
Q=ρV(1-ε)ΔT
(8)
式中:Q为蓄热量;ρ为月壤密度;V为蓄热器体积;ΔT为蓄热器的平均温升。
考虑到两者泵功的差异,为了更进一步综合比较两种堆叠方式的蓄热性能,可引入无量纲综合蓄热指数γ0:
(9)
式中:C为月壤比热容;k为常数;m为月壤质量;ΔP为蓄热器进出口压差;QV为体积流量。
由于在相同蓄热时间下,泵功与ΔP·QV成正比,比例系数为常数k,因此γ0代表的意义为单位泵功下蓄热器蓄热量的增加。由于m、C、k均为常数,为方便计算,用γ表示综合蓄热指数。表4给出了平均温升和综合蓄热指数γ的结果。从综合蓄热指数γ来看,SC堆叠方式比FCC堆叠方式高出30.2%,因此 SC堆叠优于FCC堆叠。
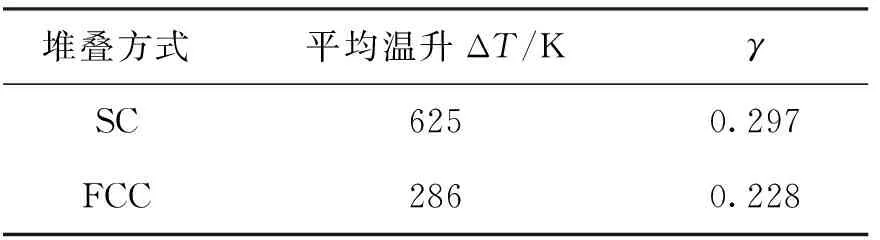
表4 模拟结果
2.2 月壤蓄热球直径对蓄热效果的影响
图8给出了不同进出口压差下(ΔP=200 Pa,1 000 Pa,5 000 Pa)蓄热器的蓄热指数γ与月壤球直径的关系,蓄热时间均为20 h,入口氦气温度为1 000 K,均为SC堆叠方式。由于多孔介质的孔隙率仅和堆叠方式有关,与月壤球的直径无关,所以图中不同直径月壤球堆叠的蓄热器孔隙率均相同(ε=0.476)。从图中可以看到,在相同进出口压差下蓄热器的综合蓄热指数γ随着直径的变化存在先增再减的趋势。这是因为在相同体积的蓄热器中,孔隙率不变,月壤球体直径的大小影响的是界面密度,即单位体积多孔介质与流体的换热面积的大小,也影响惯性阻力和粘性阻力的大小,球直径增大时氦气的流动阻力减小,但换热效果变差,直径减小时则反之。同时从图中还可以发现,每一种进出口压差均存在月壤球直径最优值使得蓄热器蓄热指数最高。200 Pa、1 000 Pa、5 000 Pa三种进出口压差下对应的最佳月壤球直径分别是5 cm、1 cm、0.5 cm。当月壤球直径小于最优直径时,直径的增大致使阻力减小,通过蓄热器的热介质流量更大,蓄热量增加,因此γ值逐渐增大;当月壤球直径大于最优直径时,直径的增大致使换热面积减小,蓄热量减少,因此γ值逐渐减小。

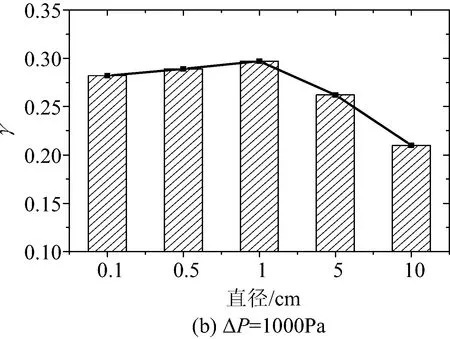

图8 不同进出口压差下综合蓄热指数γ随月壤球体直径的变化Fig.8 Variation of γ with regolith ball diameter under different pressure difference
从图8中还可以发现,月壤球体的最优直径随着进出口压差的变化而发生改变,图9给出了最优直径随压差变化的关系。可以看到,月壤球体的最优直径随着进出口压差增加而非线性地减小。出现上述结果是因为流体的流动阻力随着月壤球直径的减小而增大,但流体与月壤球的换热能力会随着换热面积的增加而增大,在较大的进出口压差下,月壤球直径减小带来换热能力的增加不如阻力增大得快,因此为了减小泵提供的进出口压差,需要适当增大月壤球的直径,以获得最佳的综合蓄热指数γ。
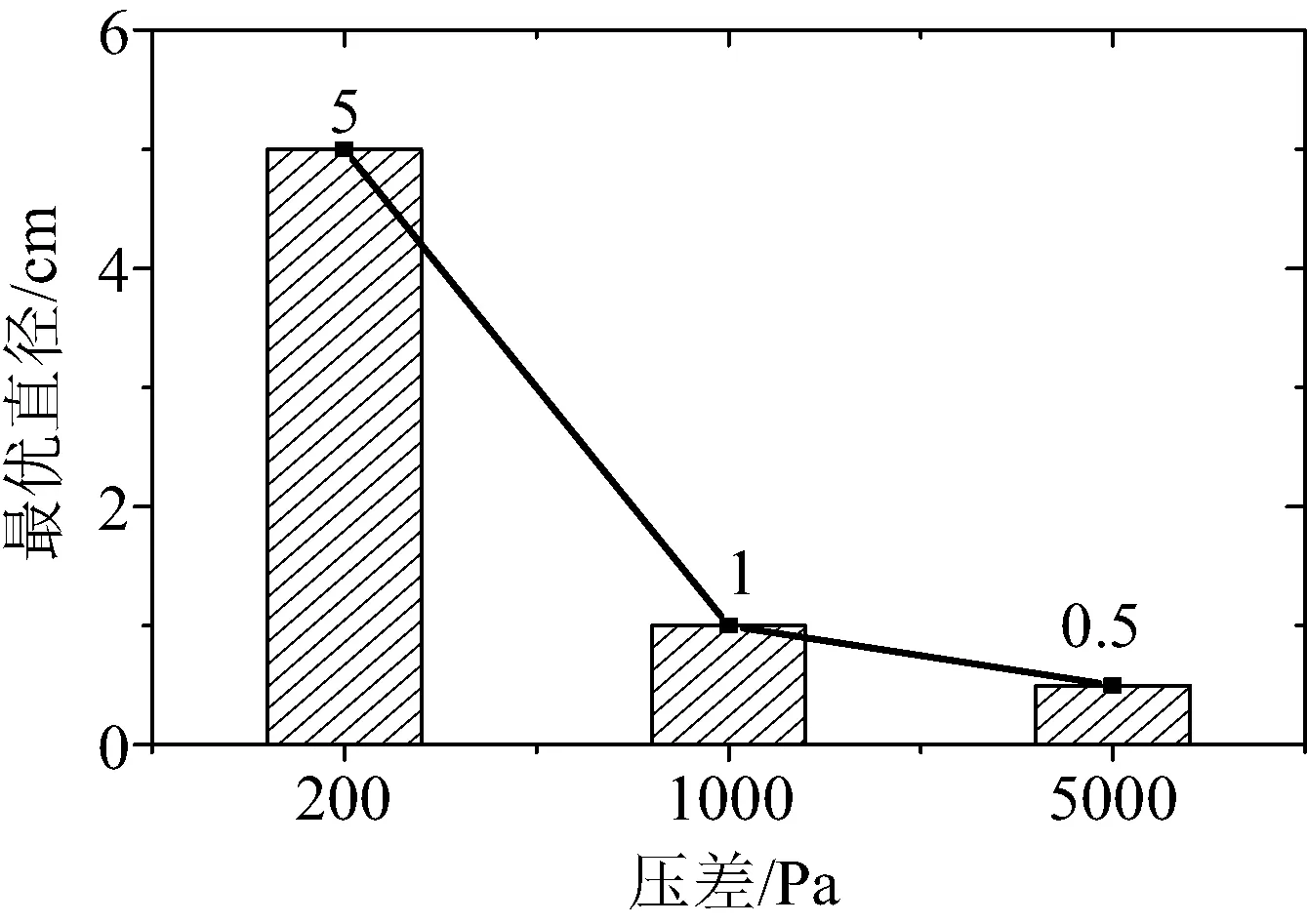
图9 最优直径随压差的变化Fig.9 Variation of optimum diameter with pressure difference
同时从图9中还可以发现,当进出口压差从200 Pa增加到1 000 Pa时,月壤球的最优直径从5 cm减小到1 cm,当进出口压差从1 000 Pa增加到5 000 Pa时,月壤球的最优直径从1 cm减小到0.5 cm。这表明随着进出口压差的增加,最优直径的变化幅度逐渐减小,说明压力增大到5 000 Pa后,直径大小对综合蓄热指数的影响越来越小。
2.3 最优直径下蓄热量随时间的变化
为了进一步分析蓄热器动态蓄热特性,图10给出了蓄热器的平均温度Tav在三种进出口压差(200 Pa,1 000 Pa,5 000 Pa)下随时间的变化,所采用的月壤球的直径分别为对应压差下的最优直径(5 cm,1 cm,0.5 cm),月壤球堆叠方式为SC方式,总蓄热时间20 h,蓄热器初始温度均为150 K。从图中可以看出,三种进出口压差下,蓄热器的平均温度随着时间在开始阶段呈现线性增加趋势,在后期阶段开始变缓。这是因为随着平均温度增加,氦气与月壤球之间的换热温差逐渐减小。同时还可以看到,进出口压差越大,蓄热器蓄热的速度也更快,在蓄热结束时,三种进出口压差的蓄热器平均温度分别为764 K、620 K、604 K,蓄热量分别为2.34×107J、1.79×107J、1.73×107J。很明显看到相同时间下,200~1 000 Pa蓄热量的增加仅为6×105J,而1 000~5 000 Pa时蓄热量的增加较为显著,达到5.5×106J。这是由于在较低进出口压差下,使用对应最优直径的月壤球时进入蓄热器的热介质流量均较小,在增大进出口压差后,进入蓄热器的氦气流量才会明显增加。

图10 蓄热器平均温度随时间的变化Fig.10 Change of average temperature of thermal energy reservoir with time
3 结束语
本文通过数值模拟的方法研究了不同流动压降下,月壤蓄热球堆叠方式、球直径对蓄热器传热过程的影响规律和机理,得到了如下结论:
1)在相同蓄热时间下,当热介质的热量都能被蓄热器充分吸收时,SC堆叠方式的综合蓄热指数高于FCC堆叠方式。
2)月壤蓄热器在相同的蓄热时间和进出口压差下,根据综合蓄热指数γ来看,月壤球直径存在最优值,不同的进出口压差对应的最优值也不同。
3)由于随着进出口压差的减小,最优直径增大,因此为了减小泵提供的压差,应该适当增加月壤球的直径。
4)蓄热器使用更大的最优直径的月壤球蓄热时,蓄热速度更慢,对应的进出口压差更小。
