综合能源背景下风电叶片雷击防护安全研究
2020-04-09李新凯刘蔚张廷军王佩明赵健孙曼杰
李新凯,刘蔚,张廷军,王佩明,赵健,孙曼杰
(中国华电科工集团有限公司,北京 100070)
0 引言
雷击是影响风电机组安全运行的主要因素之一。风电机组的本体结构高耸突出,且常位于旷野或山区地带,是地面上容易受到雷电直击的大型金属性结构体[1]。同时,由于风电机组叶片叶尖的对地高度随机组单机容量的增大而不断增加,风电机组在空间引雷的效果明显增强。这导致大容量机组的雷击损坏事故率进一步上升[2]。欧美以及日本等国的运行数据表明[3],风力发电机组所遭受的绝大多数雷击的雷击点位于机组的叶片[4]。巨大的雷电流通常由风力发电机组的叶片注入机组,并常在叶片的内部或表面形成电弧。现代风电机组的叶片都是由复合材料,如玻璃纤维增强复合材料(俗称玻璃钢),制成的大型中空结构体。这些复合材料耐受高温的性能较差,因此电弧会造成叶片的严重损坏。据统计,由雷击引起的风电机组叶片损坏的年故障率约5%。大容量风电机组叶片的雷击防护已成为制约风电机组运行可靠性水平提升的瓶颈问题之一。
目前,风电机组叶片的防护设计主要依据国际电工委员会IEC在2002年颁布的风力发电机组防雷推荐标准IEC/TR 61400-24[5]进行。但依据IEC/TR 61400-24设计的风电机组雷电接闪防护系统存在失效率高的问题。这是因为IEC/TR 61400-24仅给出了一般性和经验性的设计原则,未充分考虑风力发电机组雷击过程上行先导产生机理和上、下行先导接闪机理,因此无法给出定量化的设计条款和具体的实施细则。
对雷击过程的机理研究最早可以追溯到1760年富兰克林发明了避雷针[6]。雷击过程的机理研究需以雷击模拟实验获得的雷击过程为基础。近年来,由于高电压实验手段不断建立和完善,雷击过程的机理研究取得了长足进展。特别是20世纪60—70年代,高压长空气间隙放电实验极大地推动了人类对雷击现象和雷击过程的认识。在此基础上,雷击过程的某个阶段(如上行先导的起始和发展)也已经被证明可以通过雷击模拟实验利用冲击高压发生器产生的双指数冲击电压波制造空气放电来模拟[7-14]。
通过对国内外风电机组雷击接闪过程及机理研究现状以及叶片接闪系统研究现状的全面分析,可以得出目前的研究还存在不足[15-16]。需要在明确风力发电机雷击接闪机理的前提下研究新型雷击接闪防护系统。
基于雷击接闪机理,本团队提出了一种在叶片外表面敷设导体的方案[17],用于屏蔽下引线起始上行先导,从而达到保护叶片本体的目的。本文基于上述研究成果,采用计算流体力学(CFD)方法研究了外敷导体直径对风力机专用翼型DU93-W-210翼型气动性能的影响规律。
1 几何模型及数值方法
1.1 几何模型
数值计算对象为DU93-W-210翼型,相对厚度21.0%,尾缘厚度0.5%。计算几何模型如图1所示。
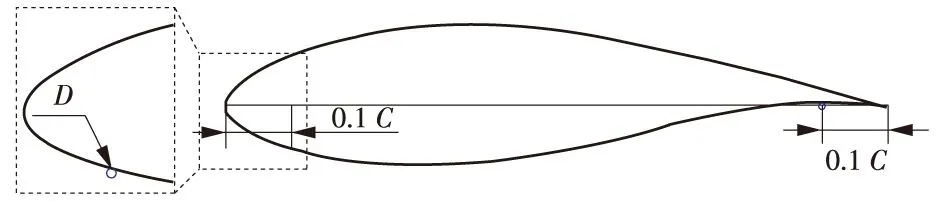
图1 计算几何模型
外置导体布置于翼型压力面(迎风面);导体距前缘、尾缘为0.1C(C为翼型弦长,C=1 m)。
导体直径用D表示,分别研究了D为2,3,4,5,6,7,8,9,10 mm时对翼型气动特性的影响。
1.2 数值方法
计算网格:采用ICEM(网格划分软件)进行全域结构网格划分,对翼型尾缘及下游部分进行网格加密处理,计算翼型为2D网格,翼型周向布置380个网格,径向布置357个网格,第1层网格高度0.001 mm,保证y+<1(y+是壁面第1层网格高度的1/3与当地流体黏度长度的比值)。计算网格如图2所示。
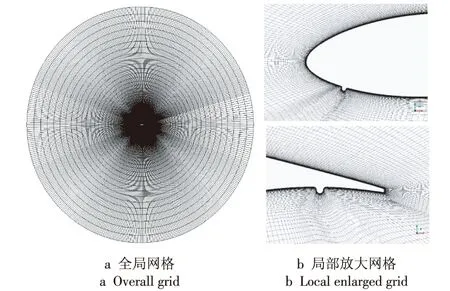
图2 计算网格
边界条件:计算域为30C。采用速度进口、压力出口边界条件,叶片表面及外置导体设置为无滑移壁面。边界条件设置如图3所示。
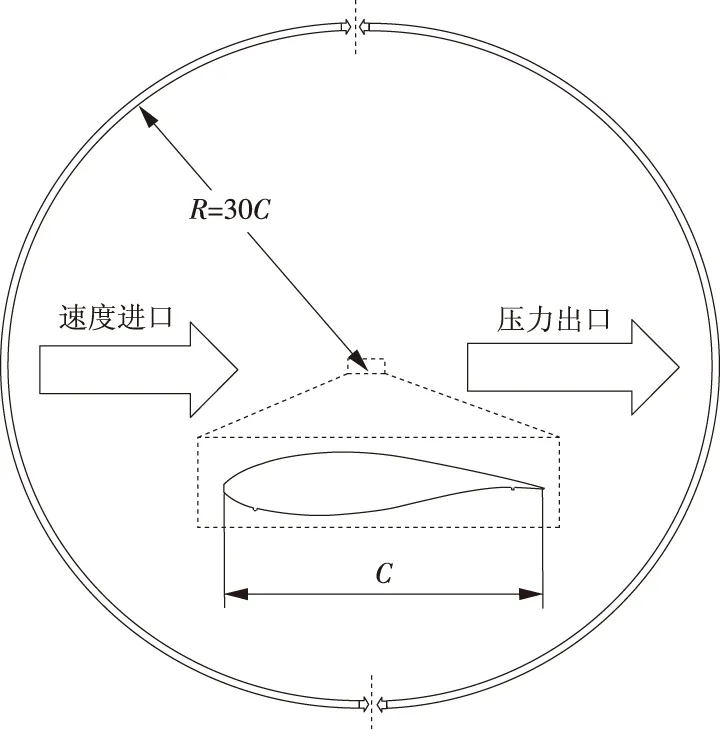
图3 计算边界条件
求解设置:基于Fluent求解器,SA(Spalart Allmaras)湍流模型,二阶精度;计算攻角:0°,4°,8°,12°,16°,20°;计算雷诺数:Re=1×107。
2 计算结果分析
2.1 数值方法验证
以未加外置导体的洁净翼型为例进行数值方法验证,风洞实验在华北电力大学风洞实验台完成,由于风洞实验数据雷诺数为1×106,所以验证时,计算雷诺数也为1×106。图4为DU93-W-210翼型气动特性,图4中:α为翼型攻角,(°);Cl为升力系数,无量纲值;Cd为阻力系数,无量纲值。从图4中可以看出,在翼型最大升力系数处(8°攻角),计算值与实验值差别较大。在其余攻角时,无论是升力系数还是阻力系数与实验值差别较小,从而验证了数值方法的可靠性。
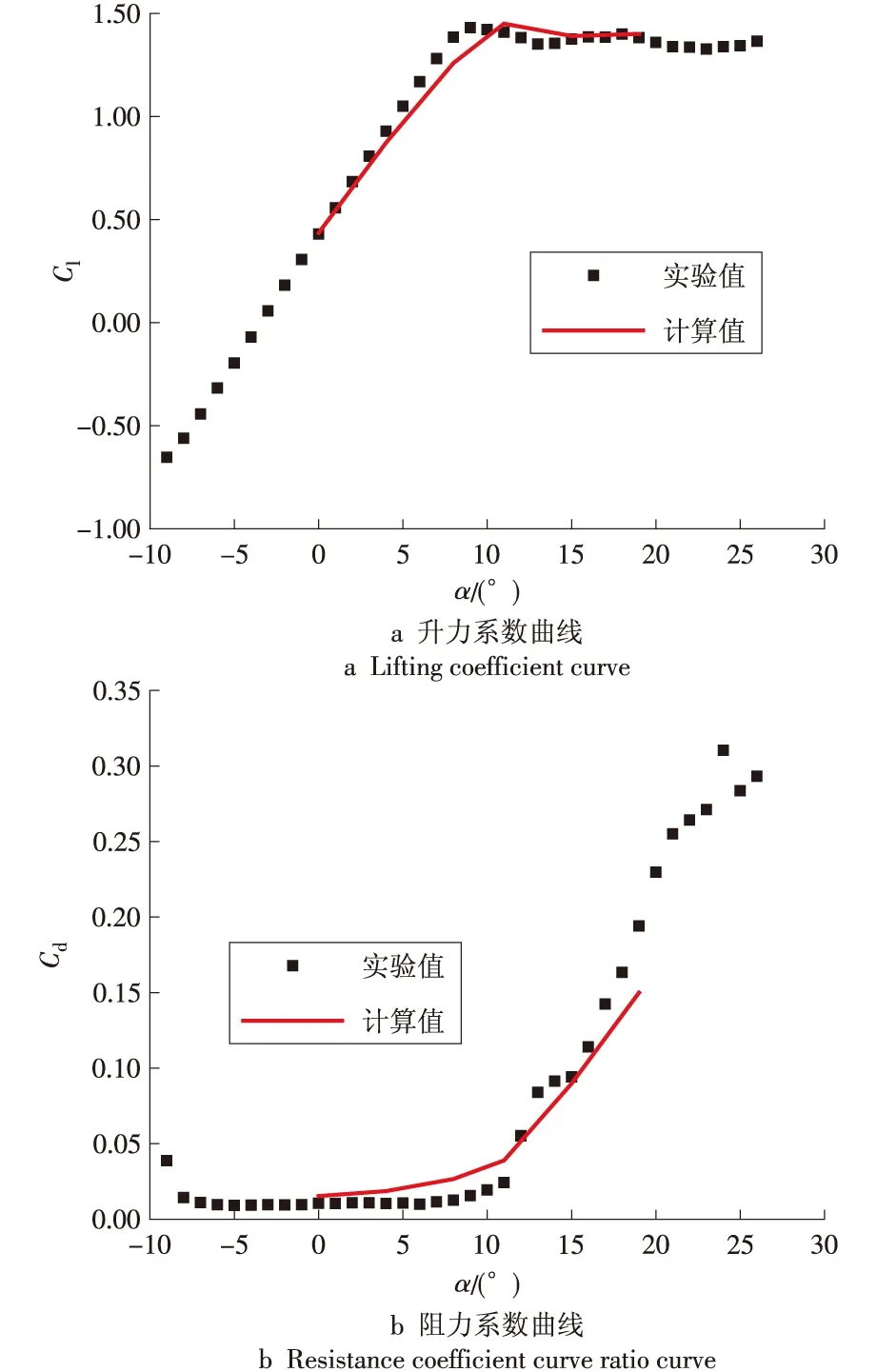
图4 DU93-W-210翼型气动特性
2.2 结果分析
图5翼型气动特性随攻角的变化规律,图例中:“无导体”表示未敷导体翼型;2 mm,3 mm等表示翼型外敷导体直径。由图5可见,当翼型雷诺数为1×107,无导体翼型失速攻角约16°时,最大升力系数可达1.90左右。当翼型外敷导体后,在翼型升力系数的线性段,升力系数的绝对值差别较小,只有在20°攻角时差别较大。阻力系数在0°,20°攻角时差别较大,其余攻角时阻力系数绝对值差别不大。升阻比基本随导体直径线性降低,最大升阻比对应的攻角为4°。当D=10 mm,在攻角等于20°时,翼型升力系数下降,阻力系数增加,升阻比降低;当D=2~9 mm,在攻角等于20°时,升力系数增加,阻力系数变化较小。
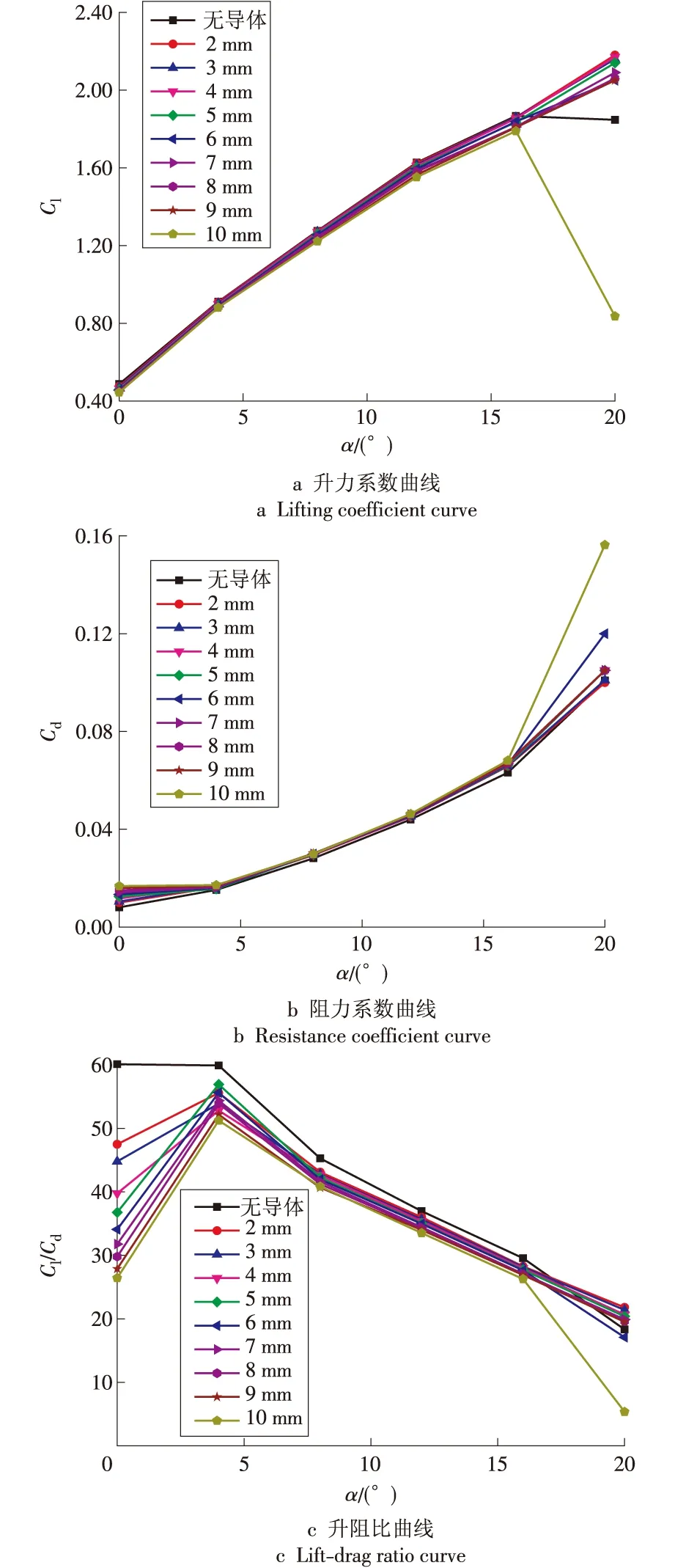
图5 翼型气动特性随攻角的变化规律
图6为翼型气动特性随导体直径的变化规律。图中,横坐标为不同导体直径,纵坐标分别为升力系数、阻力系数、升阻比。由图6可见,随着导体直径D的增加,翼型升力系数总体上呈下降趋势,阻力系数呈上升趋势,升阻比下降;翼型升力系数、升阻比基本与导体直径呈线性变化趋势;0°攻角时,升力系数变化趋势与其余攻角相差不大,阻力系数增加斜率变大,升阻比下降斜率最大。
图7是不同导体直径的翼型气动特性较洁净翼型的变化率。横坐标是导体直径,纵坐标是变化率。由图可见,0°攻角时,带导体翼型升力系数下降最多,当导体直径为10 mm时,升力系数最多下降10%左右。4°~16°攻角时升力系数下降相差不多,升力系数平均下降了3%左右。20°攻角时,除了D=10 mm时,其余导体直径对应的升力系数较洁净翼型有所增加,究其原因是因为此时洁净翼型已经失速,而带导体翼型类似于转捩带作用,一定程度上抑制了翼型失速。对于阻力系数,当翼型攻角为0°时,带导体翼型阻力系数增加最大,斜率也最大。除了20°攻角,其余攻角时阻力系数变化斜率基本一致,阻力系数增加的平均值在7%左右。对于升阻比,除了20°攻角,其余攻角带导体翼型升阻比均有所下降。0°攻角时,升阻比下降斜率最大,最大升阻比在D=10 mm时,下降约56%。4°~16°攻角时升阻比平均下降7%左右。

图7 不同导体直径的翼型气动特性较洁净翼型的变化率
图8为不同导体直径的翼型截面速度云图。由图可见,导体对翼型绕流场的影响主要集中在导体下游速度场。随着导体直径的增加,导体下游的低速区范围逐渐扩大。
图9为4°攻角时,不同导体直径的翼型表面压力系数分布(图中,横坐标为当地位置x与翼型弦长C之比;纵坐标Cp为翼型表面压力系数)。导体对翼型一周压力系数的影响主要集中在导体上、下游。由于导体存在,在导体上游翼型表面压力变高,导体下游翼型表面压力变低。这是由于外置导体,在翼型压力面导体下游产生了不同程度的分离旋涡,旋涡尺度大小与导体直径成正比;在翼型压力系数曲线上,导体前由于流体集聚,压力增加,导体下游形成的涡核为低压区。不同导体高度之间的压差变化也较小。

图8 不同导体直径的翼型截面速度云图
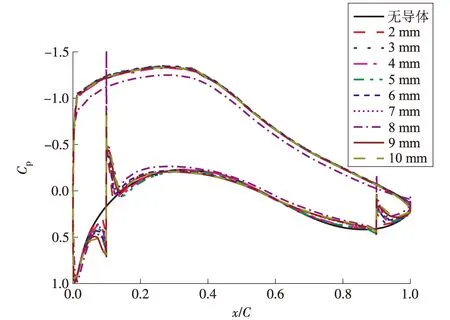
图9 4°攻角时不同导体直径翼型表面压力系数分布
3 结束语
针对目前大型风电机组叶片雷击损伤事故率高,叶片现有雷击防护系统失效率高等问题,本文提出了叶片外敷导体防雷方案,研究了外敷导体直径对风力机专用翼型气动性能的影响规律,得出以下结论:
(1)随着导体直径D的增加,翼型升力系数总体上呈下降趋势,阻力系数呈上升趋势,升阻比下降;翼型升力系数、升阻比基本与导体直径呈线性变化趋势;0°攻角时,升力系数变化趋势与其余攻角时相差不大,阻力系数增加斜率变大,升阻比下降斜率最大。
(2)0°攻角时,带导体翼型升力系数下降最多,当导体直径为10 mm时,升力系数最多下降约10%。4°~16°攻角时升力系数下降相差不大,升力系数平均下降约3%。20°攻角时,除了D=10 mm时,其余导体直径对应的升力系数较洁净翼型有所增加。对于阻力系数,当翼型攻角为0°时,带导体翼型的阻力系数增加最大,增加斜率也最大。除了20°攻角,其余攻角对应的阻力系数变化斜率基本一致,阻力系数增加的平均值在7%左右。对于升阻比,除了20°攻角,其余攻角对应的带导体翼型的升阻比均有所下降。0°攻角时,升阻比下降斜率最大,最大升阻比在D=10 mm时,下降约56%;4°~16°攻角对应的升阻比平均下降约7%。
(3)导体对翼型绕流场的影响主要集中在导体下游速度场。随着导体直径的增加,导体下游的低速区范围逐渐扩大。
