极大Smith符号图的Smith群和临界群
2020-04-09,
,
(湖南师范大学 数学系,湖南 长沙 410081)
1 研究背景
随着临界群在物理、经济等不同领域的广泛应用,近些年来,越来越多的学者开始对连通图的临界群和Smith群进行研究,并发现临界群和Smith群是连通图的精细不变量。目前,对于连通图的临界群和Smith群已有较多研究成果,比如莫比乌斯阶梯图Mn[1]、Peisert图[2]、迭代锥[3]、Kneser图[4]、门槛图[5]、Dihedral图[6]、圈的平方[7]、等多种类型图的临界群。除此之外,对于临界群上的代数性质也有相关研究,比如临界群的秩[10]。
一个图G的点集和边集分别由V(G)和E(G)表示,一个符号图Г=(G,σ)由一个无符号图G=(V,E)和一个符号函数σ:E(G)→{+1,-1}组成,如果σ(e)=+1,那么边e是正的,如果σ(e)=-1,那么边e是负的。
设连通符号图Г有n个顶点,那么图Г的邻接矩阵是n×n阶的对称矩阵A(Г),其中aii=0,i∈{1,2,…,n};aij=+1,i,j∈{1,2,…,n},当且仅当顶点vi和顶点vj之间连正边;aij=-1,i,j∈{1,2,…,n},当且仅当顶点vi和顶点vj之间连负边。连通符号图Г的Laplacian矩阵定义如下:L(Г)=D(Г)-A(Г),其中D(Г)=diag(d1,d2,…,dn)是连通符号图Г的度矩阵。
将连通符号图Г的邻接矩阵A(Г)看作Zn→Zn的群同态,余核cokerA(Г)=Zn/(A(Г)Zn)称为Г的Smith群。类似地,将连通符号图Г的Laplacian矩阵L(T)看作Zn→Zn的群同态,它的余核cokerL(Г)=Zn/(L(Г)Zn)是Г的临界群。
根据连通符号图的Smith群和临界群的定义可知,对其邻接矩阵和Laplacian矩阵分别作行列整变换,可以得到其Smith群和临界群的代数结构。除此之外,课题组还可以通过找Smith群和临界群的生成元及其阶数的方法来得到其代数结构。
特征值在[-2,2]的符号图叫做Smith符号图[11],由T2n、S14和S16的子图构成。在本文中课题组完全确定了极大Smith符号图T2n的临界群和Smith群的代数结构。其中符号图T2n、S14和S16分别与图1a,1b和1c所示的符号图转换等价图,图1b和图1c中的实线和虚线分别表示两个顶点之间连正边和负边。

图1 符号图的转换等价图Fig.1 Transformation equivalence graph of signed graph
S14和S16是有限连通符号图,它们的Smith群和临界群较易得到。S14的Smith群和临界群分别是和;S16的Smith群和临界群为和。
2 T2n的Smith群和临界群
由图1可以写出T2n的邻接矩阵,其中A(Cn)是圈Cn的邻接矩阵,。
因为A(T2n)2=4I,所以T2n的Smith群的初等因子是4的素因数的幂,故可设又因为,所以有

其中rank2(A(T2n))是A(T2n)在二元域中的秩。
定理 1
证明1)当n≡1 mod 2时,
①当n≡1 mod 4时,令
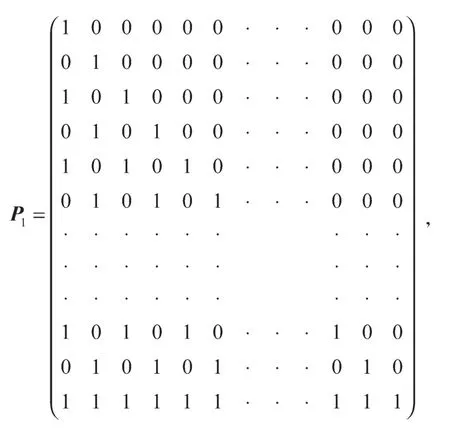

②当n≡3 mod 4时,令

2)当n≡0 mod 2时,
①当n≡2 mod 4时,令

②当n≡0 mod 4时,令


综上所述有
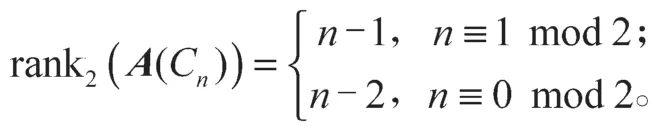
定理2
证明令,则,
即
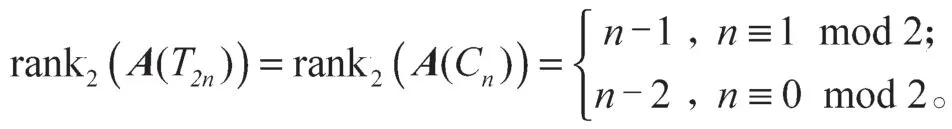
定理3T2n的Smith群的代数结构为

证明1)n≡1 mod 2时,rank2(A(T2n))=n-1,则
2)n≡0 mod 2时,rank2(A(T2n))=n-2,则
综上所述,T2n的Smith群的代数结构为

T2n的Laplacian矩阵为
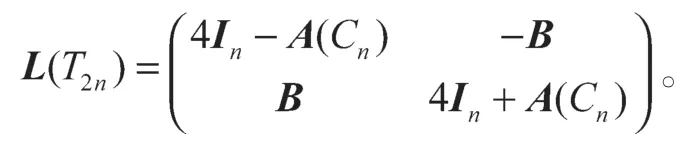
定理 4T2k的临界群的代数结构为

证明因为A(T2n)2=4I,所以A(T2n)的特征值只可能为±2,且A(T2n)的迹为0,所以特征值+2和-2的重数均为n。又因为L(T2n)=4I-A(T2n),所以L(T2n)的特征值为2和6,其重数均为n,所以有detL(T2n)= 2n×6n=12n=4n×3n。由A(T2n)2=4I可以得知(L(T2n)-8I)L(T2n)=12I。从而T2n的临界群的初等因子为2,22,3,且可设,其中
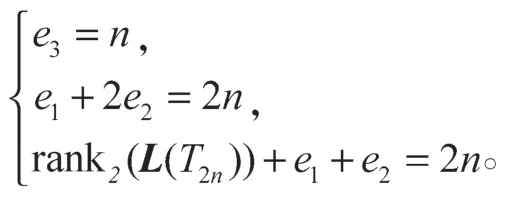
由定理2可知
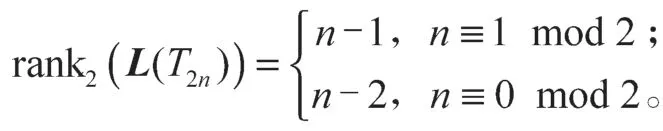
当n≡1 mod 2时,可得

从而有

当n≡0 mod 2时,可得从而有
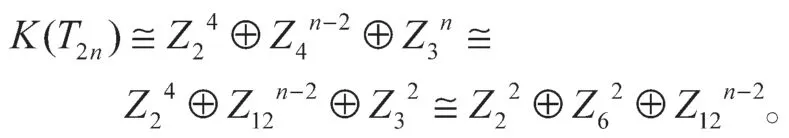
3 结语
本文从临界群和Smith群的角度,运用初等变换分别得到了T2n的Smith群和临界群。如果将T2n推广到一般符号图,则暂时无法用矩阵的初等变换解决。因此,得到任意一个符号图的临界群和Smith群结构是一个十分吸引人和值得深入研究的课题。
