图上算术结构的电阻距离矩阵

，，

（湖南师范大学 数学系，湖南 长沙 410081）

1 背景知识

对于一个简单图G=(V,E)，若列向量对，则称(d,r)为图G的算术结构，如果满足：

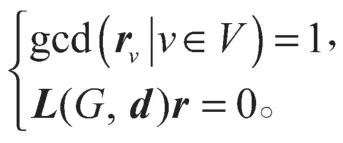
注意：列向量d和r的所有分量都是正整数，且d和r相互确定。(G,d,r)叫做算术图，L(G，d)是其算术结构的拉普拉斯矩阵。任何图G都有拉普拉斯算术结构，即(d,r)=(degG,1)，d=degG表示图G的度向量，r=1为全是1的列向量。

令矩阵BT表示矩阵B的转置，A是一个m×n的矩阵，n×m的矩阵G被称为是A的广义逆，如果满足AGA=A。

一个n×m的矩阵G被称为是A的Moore-Penrose逆，如果满足以下条件：

i）AGA=A；

ii）GAG=G；

iii）(AG)T=AG；

iv）(GA)T=GA。

我们用A+表示A的Moore-Penrose逆。

图的算术结构的概念，是D.J.Lorenzini[1]研究代数几何中退化曲线时出现交矩阵而引入，更多可参见文献[2]中的几何观点。其后，关于算术结构的研究，吸引了很多学者，如在文献[1]证明了简单连通图上的算术结构个数是有限的；文献[3]研究了路和圈上的算术结构个数的精确值等。

图距离的研究在图论中是非常重要的内容之一[4-9]。电阻距离是图的距离，在图的随机游动、网络连通性、物理学等各个领域都有研究，如文献[4]和文献[5]。本文在R.B.Bapat的文献[6]和[7]的研究基础上，将一般连通图G上的电阻距离和电阻距离矩阵扩展到算术图上。首先，利用算术结构的拉普拉斯矩阵定义一个算术结构的电阻距离ρ(i,j)，再用图的算术结构的电阻距离ρ(i,j)表示矩阵中位置元素(i,j)，得到其算术结构的电阻距离矩阵H，并最终求出它的逆矩阵。

2 算术结构的电阻距离

首先，回顾一下经典距离满足的公理：

令G是一个顶点集为V(G)={1,2,…,n}的连通图，且令d∶V(G)×V(G)→R，如果d表示两个顶点之间的一个度量，那么d应该满足如下条件：

i）对于所有的i、j有d(i,j)≥0，当且仅当i=j时等号成立；

ii）d(i,j)=d(j,i)；

iii）d(i,j)+d(j,k)≥d(i,k)。

接下来定义一个n×1向量rij，对于i，j∈{1,2,…,n}且i≠j，第i项为，第j项为，其余项为0。

在定义算术结构的电阻距离之前，先证明一个关于L(G,d)广义逆的结论。

引理1令G是一个连通图，V(G)={1,2,…,n},L(G,d)是G的算术结构的拉普拉斯矩阵，令i，j∈{1,2,…,n}且i≠j。若M1、M2是L(G,d)的任意两个广义逆，则。

证明对于L(G,d)的任意两个广义逆矩阵M1、M2有

L(G,d)M1L(G,d)=L(G,d)M2L(G,d)=L(G,d)。由rijTrij=0，可知rij在L(G,d)列空间中。所以存在一个列向量z，使得rij=L(G,d)z。

所以有

故恒有

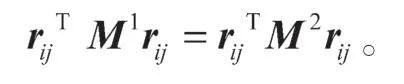
由引理1证明可知：对于L(G,d)的任意一个广义逆H而言，rijTHrij是不变的。

下面给出了i、j之间的算术结构的电阻距离：

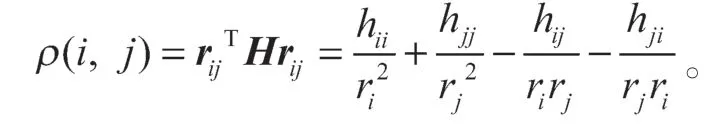
式中，H为L(G,d)的任意一个广义逆。

若i=j，ρ(i,j)=0。

若H是L(G,d)的一个对称广义逆，有

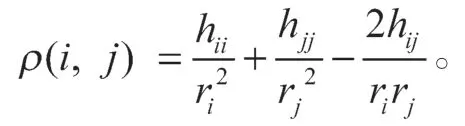
特别地，令H=L(G,d)+，有

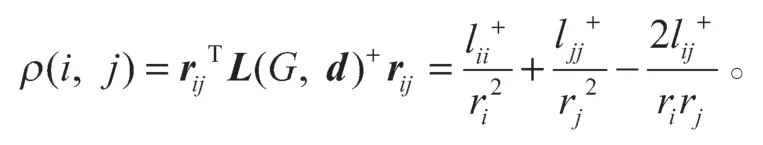
下面证明定义的算术结构的电阻距离也满足经典距离的3个条件。在证明满足条件之前，先证明一个有用的结论。

令A是一个n×n阶矩阵，可被分块成如下形式：

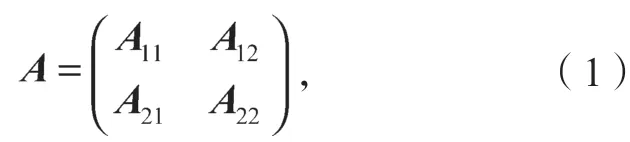
式中A11、A22为方阵。

若A11是非奇异的，那么矩阵A22-A21A11-1A12为A11在矩阵A中的Schur补。同理，如果A22是非奇异的，那么矩阵A11-A12A22-1A21为A22在矩阵A中的Schur补。

引理2设G是一个有n个顶点的连通图，并设L(G,d)是G的算术结构的拉普拉斯矩阵，若B为L(G,d)的一个任意的真主子阵，则B-1为一个元素非负的矩阵。

证明令B是L(G,d)的一个k×k主子阵，其中1≤k≤n-1，由于det(B)＞0，则B是非奇异的。下面通过对k用归纳法来证明。

当k≤2时，显然成立。

假设对于阶数小于k的主子阵，该结论成立，接下来只需证明B的所有k阶余子式均非负即可。

B的一个对角线元素的代数余子式为L(G,d)的主子阵的行列式，且均为正。下面证明B的(1,2)-位置元素的代数余子式为非负的，其余的代数余子式证明方法与此类似。

则

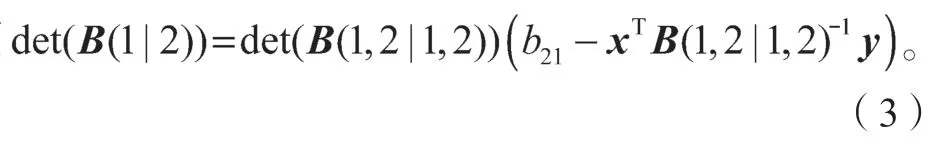
故B的(1，2)-位置元素代数余子式为非负的。

下面证明算术结构的电阻距离满足经典距离的3个公理。

定理1上面定义的电阻距离ρ仍满足经典距离的3个公理。

证明若n≤2，这些性质很容易证明。下面假设n≥3。

令L(G,d)是G的算术结构的拉普拉斯矩阵，L(G,d)+是L(G,d)的Moore-Penrose逆。

由于L(G,d)是对称的，则L(G,d)+也是对称的。此外，L(G,d)是半正定的，则L(G,d)+=L(G,d)+L(G,d)·L(G,d)+也是半正定的。因此有ρ(i,j)≥0。

由L(G,d)=L(G,d)L(G,d)+L(G,d)和L(G,d)+=L(G,d)+L(G,d)L(G,d)+，有

又由rank(L(G,d))=n-1，可得rank(L(G,d)+)=n-1。

又因为L(G,d)+的任意2×2阶主子式皆为正，即对于任意的i≠j，有。

再由算术平均-几何平均不等式可知：

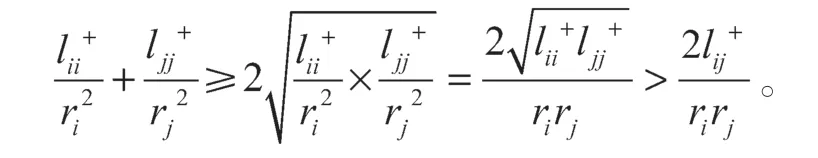
由于rij=-rji，故很容易得到ρ(i,j)=ρ(j,i)，满足条件 ii）。

对于L(G,d)的任意一个广义逆L'，下证

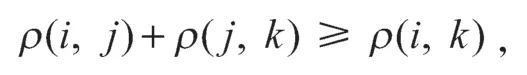
即证：

在L(G,d)中，用0去替换第j行j列元素，并用B-1去替换L(G,d)(j|j)，令得到的矩阵为L'，易证

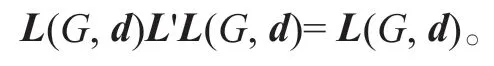
所以L'为L(G,d)的一个广义逆，因此有。

又由于B-1≥0，所以。

3 算术结构的电阻距离矩阵

前面已经给出了算术结构的电阻距离，本节将给出算术结构的电阻距离矩阵的表达式及其逆矩阵的公式。

首先定义算术结构的电阻距离矩阵H。

定义 1令G是一个顶点集为V(G)={1,2,…,n}的连通图，H=(ρij)为算术结构的电阻距离矩阵，其中。

下面介绍一些符号。令L(G,d)是G的算术结构的拉普拉斯矩阵，C=rrT，α=rTr，其中r=(r1,r2,…,rn)T。

由于算术结构的拉普拉斯矩阵的性质与拉普拉斯矩阵相似，利用算术结构的特征向量很容易得到这个矩阵是非奇异的。

令

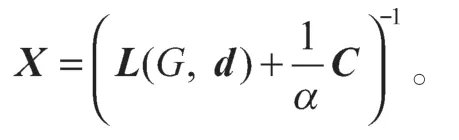
命题 1设(d,r)为连通图G的算术结构，L(G,d)为算术结构的拉普拉斯矩阵，则

证明由

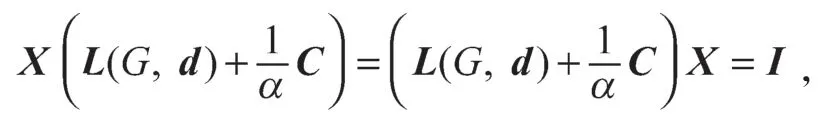
可得Xr=r，

所以有

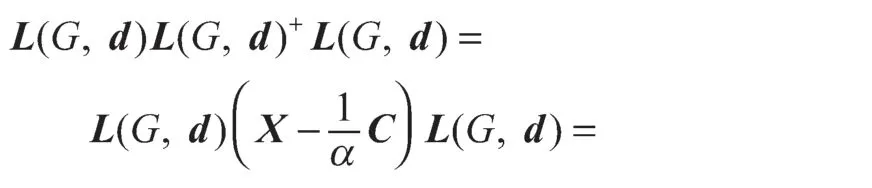
令P=diag(r1,r2,…,rn)，1是一个全为1的列向量，J=1×1T，，由上面的符号，可以得到H的矩阵表达式。

引理3。

证明由于，故的(i,j)-元素为

引理4。

证明由和，可得：

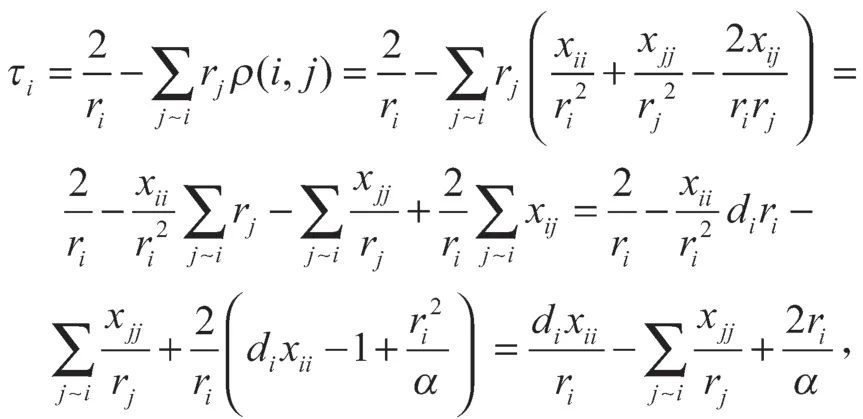
引理5。

证明由前面的证明可知：

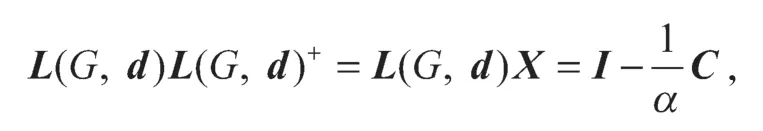
由PJ=P11T=r1T，故

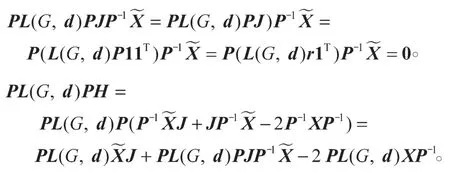
所以有

容易得到

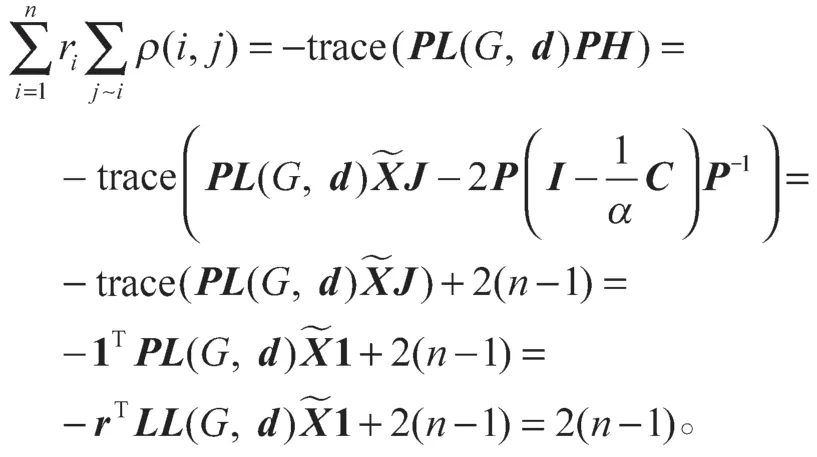
推论1rTτ=2。

证明利用前面的结论可以得到：

故rTτ=2。

由前面的定理和证明得到了下面H逆矩阵的表达式。

定理2

证明由前面的证明，有

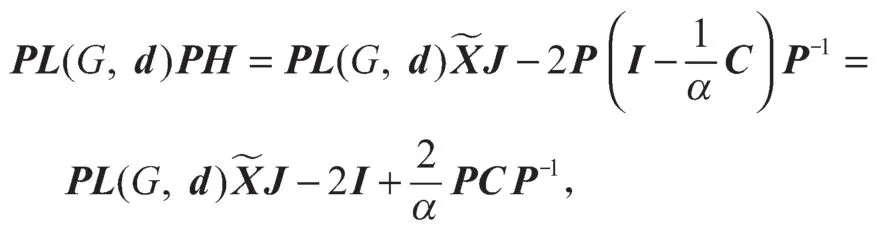
所以

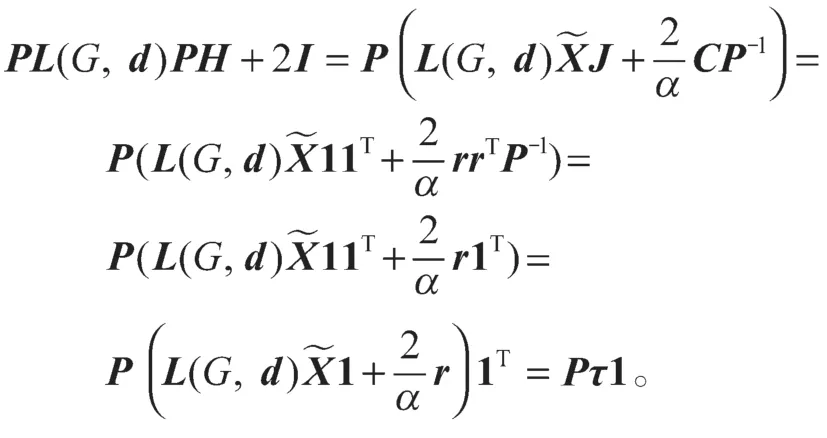
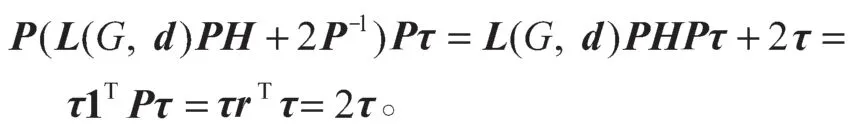
所以有L(G,d)PHPτ=0，又由L(G,d)r=0，则一定存在标量b，使得PHPτ=br。

又由τTPHPτ=bτTr=2b，得

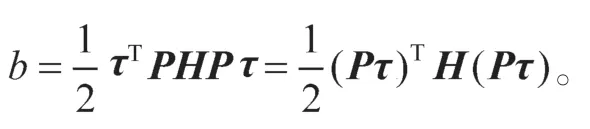
所以有

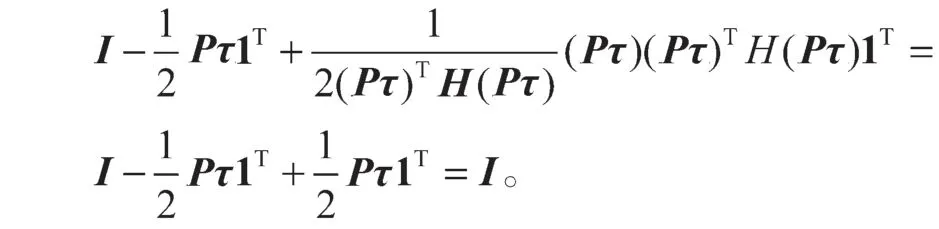
故有

4 结语

本文将一般连通图G上的电阻距离和电阻距离矩阵扩展到算术图上。先通过利用算术结构的拉普拉斯矩阵的广义逆定义一个电阻距离ρ(i,j)，之后定义了算术结构的电阻距离矩阵并得到了一些关系式，最后讨论了算术结构的电阻距离矩阵的逆和算术结构的拉普拉斯矩阵之间的关系。