基于解耦算法的化学非平衡流并行数值模拟

田壮壮，王光学,2，张怀宝，张 帆

(1. 中山大学物理学院，广州 510006；2. 国防科技大学空天科学学院，长沙 410073；3. 中山大学航空航天学院，广州 510006)

0 引言

解耦算法又称为时间分裂算法或算子分裂法[1]。在此类方法的计算中，半离散化得到的常微分方程组被分解为刚性和非刚性两部分，而后进行独立求解。刘君等[2-3]构造了一种化学非平衡流解耦算法，这种算法将化学非平衡流的内能中与温度无关的能量，即有效零点能或化学焓分离出来，添加到化学反应源项中。进而引入等效比热比，构造了在形式上与量热完全气体完全相同的能量与压力的关系式，并用等效比热比计算等效声速。进行时间分裂后，物理问题被分解成流动(非刚性)和化学反应(刚性)两部分，流动控制方程的求解与量热完全气体的求解方法完全相同，而且流动方程与化学反应方程都具有明确的物理意义。

利用这一解耦算法，刘君[3]对冲压加速器中的化学非平衡流进行了数值模拟。其中，流场空间离散采用ENO格式[4]，化学反应采用梯形公式计算；并分别采用7组分8反应的氢气/空气反应机理和13组分32反应的甲烷/空气反应机理描述化学反应过程；随后又采用19组分65反应甲烷/空气反应机理进行了模拟[5]。基于同样的解耦方法，在国内首先对钝头体激波诱导振荡燃烧现象进行了数值模拟，得到了准确的非定常振荡燃烧现象[6]；在化学动力学模型对氢气/空气超声速燃烧模拟的影响方面进行了研究[7]。应用上述解耦算法，孙明波等[8]采用5阶WENO格式[9]进行空间离散，对钝头体激波诱导振荡燃烧进行了模拟。

通过采用上述的解耦算法，化学非平衡流求解器对流动控制方程(非刚性)和化学反应源项(刚性)分别采用合适的方法求解，流动方程求解不受化学反应时间尺度的影响，从而在保证计算精度的前提下提高了计算效率；但是在复杂问题的数值计算中，化学反应源项的存在导致整体计算量显著大于量热完全气体数值模拟的计算量。本文对化学非平衡流解耦算法的非结构网格有限体积法求解器进行MPI并行化，以便为更复杂的化学反应流动数值模拟提供工具。

1 控制方程和解耦算法

本文计算中求解的微分形式二维轴对称欧拉方程可以写为

(1)

其中

式中，Q表示守恒变量，S和Qf表示反应源项和轴对称方程源项；E和F分别表示x和y两个方向的对流通量；σi表示第i个组分的化学反应速率。此外，u和v分别为x和y方向的速度，p为压力，ρ为混合气体的总密度，ρi为第i个组分的密度。单位质量总能是

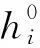
财务会计与管理会计有着紧密的联系，工作中也存在相似性，推动转型并不是对财务会计进行否定，而是将财务会计以及管理会计的优点进行融合。在保证企业会计信息公开、透明的同时，为企业战略的制定提供强有力的科学依据。因此应当对使用的财务资料格式进行适当的设计和调整。

引言中介绍的解耦算法定义等效内能为

(2)

进而可将能量方程改写为

(3)

基于同样的关系，还可以定义等效比热比

(4)

最终将控制方程改写为

(5)

其中

基于时间分裂法，可以将上述基于等效内能的控制方程分裂为流动方程和化学反应方程

(6)

(7)

对上述两个方程分别进行求解，并且依据Strang分裂格式

Q′,n+1=Lc(Δt/2)Lf(Δt)Lc(Δt/2)Q′,n

(8)

的顺序进行计算。其中，Lc和Lf分别为化学反应算子和流动算子，n表示第n个时间步。如引言所述，流动算子可以是量热完全气体流动求解中采用的各类2阶时间精度离散方法(显式[4]或隐式[8])，而化学反应算子可以采用各类刚性常微分方程组求解算法。两类算子通过式(8)所示的顺序进行计算，可以确保化学非平衡流求解的整体二阶时间精度。

2 并行计算

在数值模拟中，区域分解法是一种常用的并行算法。其基本思想是：将整个计算区域分成N个子域并相应地分配给N个计算进程，每个进程计算各自子域的流场；计算时各个进程之间进行必要的数据通信。为提高区域分解法的效率，需要尽量使各个进程的负载均衡，并减少进程间的通信。本文使用常用的METIS分区软件来实现区域分解，获得大小均衡的计算子域，从而保证分区间的负载均衡；同时，要使分区间的连接尽可能简单，从而减少分区间的通信。

图1给出了网格分区的一个例子。方形区域内的三角形网格被分为A、B两个分区，如图1(a)所示。初始分区A、B中没有重合的单元。由于使用空间2阶格式进行计算，在计算一个单元的通量时，需要用到直接相邻单元的物理量及其梯度；而计算直接相邻单元的物理量梯度时需要第二层相邻单元的物理量。这里称两层相邻单元为计算分区的“外部单元”，称分区原有单元为“内部单元”，分别如图1(b)、(c)所示。其中，标记为1的是直接相邻单元，标记为2的是第二层相邻单元。为了减少计算过程中的通信次数，需要存储外部单元的物理量。因此，各个进程存储的子域网格是分区内部单元和外部单元的总和，分别如图1(d)、(e)所示。

(a)初始分区

(b)A分区的外部单元

(c)B分区的外部单元

(d)最终的A分区

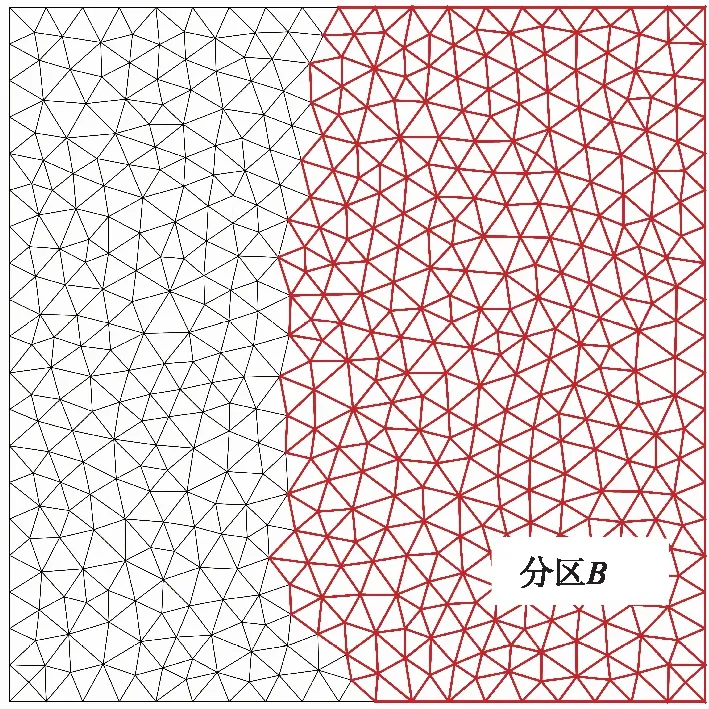
(e)最终的B分区图1 网格分区示例Fig.1 Schematic of grid partitioning

从图1中容易看出，对于多个计算分区，一个分区的外部单元必定是另一个分区的内部单元，而一个分区的内部单元可能对应着多个分区的外部单元。计算中，在每一步时间推进后，外部单元上的物理量需要从所对应的内部单元获得，以保证不同子网格间流场物理量的一致性。因此，在进行网格分区时，需要建立所有分区间的内部单元和外部单元的映射关系。

各个进程都额外存储了外部单元网格，因此，不同子域网格间是相互交错重叠的，各个子网格的网格数之和大于原始网格数。由此易知，即使排除负载不均衡和进程间通信的影响，也难以达到理想的并行加速比。

在化学非平衡流的计算中，化学反应源项求解的计算量往往显著大于流动求解的计算量。尤其是当化学反应机理趋于复杂时，化学反应源项计算量在总计算量中的比例也随之进一步增大。化学反应源项的求解仅依赖于离散网格单元内的物理量，特别是在2阶精度有限体积法的框架下，源项仅依赖于单元内变量的平均值/格心值。因此，一个时间步内化学反应源项的求解不需要进行进程/分区间通信，从而能够提高并行计算效率。

3 数值算例

为了验证化学非平衡流并行计算程序的准确性，本文以Lehr[10]于1972年进行的激波诱导氢气/空气周期性振荡燃烧实验为依据，对计算程序进行考核。在弹道靶实验中观察到：随着弹丸飞行速度的增加，激波诱导燃烧逐渐失稳，出现周期性振荡燃烧现象；进一步增大弹丸飞行速度，激波诱导燃烧的流场又趋于稳定。实验中得到了不同飞行条件下的纹影图像和不稳定燃烧的振荡频率。本文选取Ma=4.48条件下振荡燃烧现象进行测试。

3.1 计算模型

图2 计算网格示意图Fig.2 Schematic of computation grid

实验中弹丸头部直径D=15mm，本文计算中采用轴对称模型，边界条件设置如图2所示，计算网格为500×400，网格最小尺度Δ=4.5×10-6m。超声速入口边界面元给定来流参数；由于该算例中黏性影响微弱，故弹丸表面采用滑移壁面边界条件；下游出口采用超声速出流边界，来流参数如表1所示。计算选取修正的Jachimowski[11]9组分19反应机理来描述H2/Air反应过程，其中N2作为第三体影响化学反应进程。计算采用4步Rung-Kutta方法进行时间离散，CFL数取0.6。

表1 激波诱导燃烧来流参数

3.2 数值模拟结果

图3给出了激波诱导周期性振荡燃烧的实验纹影图。可以看出，弹丸前端存在光滑的脱体激波。由于弹丸飞行马赫数略低于来流参数条件下CJ爆速，混合气体经过激波压缩后增温增压，在下游发生周期性振荡燃烧，从图3中看出，燃烧阵面呈现出规则的波纹状，在燃烧阵面和激波间存在着未燃混合气体。

图3 周期性振荡燃烧实验纹影图Fig.3 Experiment schlieren of periodic oscillating combustion

采用3.1节参数进行数值模拟，得到了驻点流线上(即对称边界)密度随时间变化曲线，如图4所示。可以看出，激波和燃烧阵面呈现出显著的周期性振荡，来流沿驻点流线通过激波后增温增压，化学反应速率增大，在诱导区内经过诱导时间后释放能量，进而发生化学反应，形成燃烧阵面。弹丸前激波到燃烧阵面间的距离即为诱导区宽度，诱导区范围由激波后的诱导时间决定，驻点流线上弹丸头激波强度接近正激波，诱导时间最短，因此驻点线上诱导区宽度最小。振荡燃烧过程中，随机扰动产生一道压缩波，由于正激波后为亚声速区域，因此该压缩波向上游传播至头激波，增强了激波强度，同时形成向下游传播的弱反射声波和一道接触间断。随着激波强度的增强，波后温度升高，诱导距离缩短，燃烧阵面靠近头激波，此时化学反应速率增大，能量释放速率的短暂增大又会产生新的向上游传播的压缩波，流场进入新一周期的振荡燃烧。此外，由于燃烧阵面的位置前移，由头激波向下游传播的接触间断到达原始燃烧阵面时，无可燃气体支持化学反应放热，因此形成了向上游传播的膨胀波，膨胀波到达激波阵面时与激波相互作用降低了激波强度，减缓了波后放热速率，诱导区宽度重新增加，燃烧阵面向下游运动，恢复至初始位置。综上所述，振荡燃烧的根本原因在于压缩波和膨胀波对激波及燃烧阵面的周期性影响。

图4 驻点线上密度随时间变化曲线Fig.4 Temporal variation of density along stagnation line

图5显示了流场及H2O2组分的密度分布。可以看出，燃烧阵面存在于激波下游，并未与激波耦合，因此无法形成稳定爆轰结构。在化学反应过程中，燃烧阵面不再保持光滑，呈现周期性振荡。图6记录了驻点处压力随时间变化曲线，提取30μs～45μs时间段内数据进行傅里叶变换，得到了周期性振荡频率为417kHz，与实验数据[10]425kHz和文献计算结果[12]431kHz符合较好，证明在并行计算条件下求解器具有良好的计算精度。

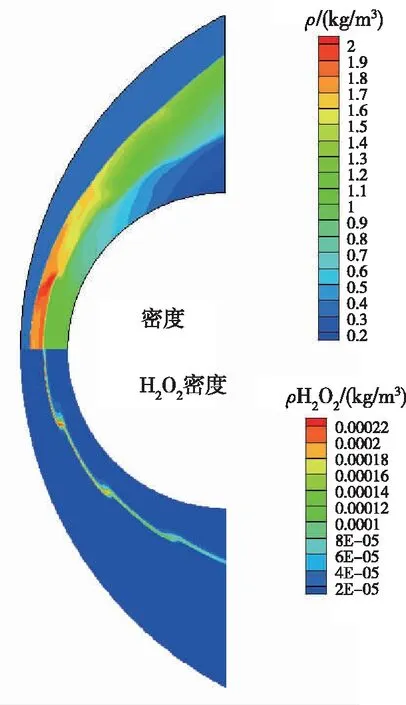
图5 振荡燃烧密度分布云图Fig.5 Density contour of periodic oscillating combustion

图6 驻点压力随时间变化曲线Fig.6 Temporal variation of the pressure at stagnation point

3.3 计算效率分析

本文的计算是在44核、主频2.2GHz、内存128GB配置的惠普Z840工作站上完成，分别进行了串行、14核、16核和32核并行计算。

图7和表2为4种计算条件下CPU计算时间对比。可以看出，随着核心个数的增加，所占用CPU时间也相应增大，主要是因为核心数的增加引起不同进程间通信时间增大。进一步对比了流动算子和化学反应算子所占CPU时间，如图7中虚线所示。可知不同进程间通信时间的增大主要体现在流动算子的求解，而化学反应的求解受进程数量的影响较小。这一结果也支撑了前文中的观点：由于不需要进行进程/分区间通信，化学反应源项的并行求解易于实现较高的效率。

(a)总计算时间

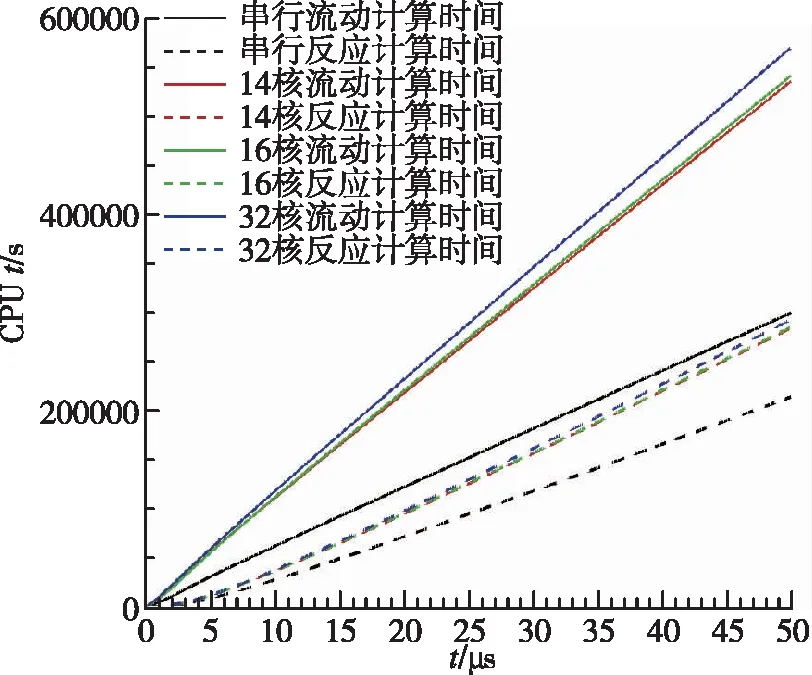
(b)流动与反应计算时间图7 周期性振荡燃烧算例CPU计算时间对比Fig.7 Comparison of the CPU time for the periodic oscillating combustion

图8和表3为3种并行计算条件下墙上时间对比。随着并行核心个数的增加，墙上时间显著减小，大大缩短了计算周期。特别是采用32核并行计算的墙上时间相对于16核并行计算的墙上时间降低了46%；而3个并行计算算例的加速比接近线性。并行计算程序与串行程序相比并未实现线性加速，这是由于并行化程序的总墙上时间中包括了(串行程序不需要的)网格分区在内的一系列功能，因此这也是程序进一步优化的重要内容。

表2 CPU计算时间对比

图8 周期性振荡燃烧算例墙上时间对比Fig.8 Comparison of the Wall time for the periodic oscillating combustion

表3 墙上时间对比

Tab.3 Comparison of the Wall time for the periodicoscillating combustion

算例墙上时间 串行14核16核32核t/s516282704536234533635

4 结论

本文介绍了作者所在研究团队在化学非平衡流数值模拟领域的研究工作。其中所采用的数值算法是目前较为先进的化学非平衡流解耦算法，能够有效地改善数值计算刚性的问题，并且已经得到多种工程问题的验证；基于该化学非平衡流求解器实现了MPI并行计算，并且基于经典算例进行了测试。结果表明，该求解器具有良好的计算精度和计算效率。后续进一步将该求解器应用于高超声速飞行器工程中，拓展其GPU并行计算的能力，实现超大规模的化学非平衡流模拟和研究。