求解物流配送同时取送货低碳选址—路径问题的量子超启发式算法

冷龙龙，赵燕伟+，蒋海青，张春苗,2，王 舜

(1.浙江工业大学 机械工程学院，浙江 杭州 310014；2.嘉兴职业技术学院 机电与汽车分院，浙江 嘉兴 314036)

0 引言

选址—路径问题(Location-Routing Problem, LRP)是供应链管理和物流系统规划中一个重要的组合优化问题，该问题处理的好坏直接影响物流配送成本、效率和客户满意度。低碳物流是考虑碳排放因素的行车路线规划和仓库选址的集合。近些年来，路径规划和选址分配问题的优化对经济、社会和环境起着重大作用。因此，本文对考虑环境因素的LRP构建数学模型，旨在减少燃料消耗以及二氧化碳等温室气体的排放量。

仓库选址分配问题(Location-Allocation Problem, LAP)和车辆路径问题(Vehicle-Routing Problem, VRP)是构成LRP的两个关键问题，两者在物流配送系统中相互影响、相互依赖和相互制约。LRP由Watson-Gandy等于1973年首次提出，目前已成为运筹管理与物流优化领域的研究热点，例如：物品回收，食品派送以及危险有毒物品配送等[1-4]。根据应用的领域，LRP衍生出许多变体，比如基本的容量约束的LRP(Capacitated LRP, CLRP)[5-6]，时间窗LRP(LRP with Time Windows, LRPTW)[7]，取送货LRP(LRP with Simultaneous Pickup and Delivery, LRPSPD)[8-9]等。然而，已有大部分LRP变型属于经典LRP范畴，即大多衍生体都以物流配送成本、客户满意度等作为优先优化的目标，并不考虑道路货物运输过程中造成的环境问题，即污染问题。鉴于此，许多研究人员致力于降低道路运输过程中的副产品——碳排放，以达到节能减排的目的，由此便形成了污染环境问题(Pollution-Routing Problem, PRP)[10]。在以往对PRP的研究中，分析燃油消耗在碳排放的重要性，往往采用将车辆燃油消耗线性转化为碳排放量，通过优化燃油消耗达到降低碳排放的目的，与此同时提出了几种模型来探讨车辆燃油消耗及其最小化，即及时燃油消耗模型(Instantaneous Fuel Consumption Model, IFCM)[11]、运行模式燃油消耗(Four-mode elemental Fuel Consumption Model, FFCM)[12]、运行速度燃油消耗模型(Running Speed fuel Consumption Model, RSCM)[11]、综合模态排放模型(Comprehensive Modal Emission Model, CMEM)[13]、排放与能量消耗模型(Methodology for calculating Transportation Emissions and Energy consumption, MEET)[14]以及道路运输燃油消耗模型(Computer Program to calculate Emissions from Road Transportation model, COPERT)[15]。以上模型分析了影响车辆燃油消耗的因素，包括汽车参数，道路状况，自然因素以及驾驶员水平与习惯等，然而能够实时准确获取以上因素是十分困难且没有必要的[16]。Xiao等[17]提出一种理想状态下的燃油消耗速率模型(Fuel Consumption Rate, FCR)，即仅考虑了距离和负载对燃油消耗的影响，大大简化了模型的复杂度并提供了一种燃油消耗的参照。然而，以上7种模型仅适用于PRP问题或低碳VRP问题，并未讨论仓库对碳排放的影响。Cagri等[18]提出了适用于LRP问题的CMEM(CMEM-LRP)模型,研究了选址问题和车型构成对碳排放的影响，并用自适应大邻域搜索算法求解。作者将燃油消耗成本转化为CLRP中的路径成本，通过优化物流配送成本从而达到降低碳排放的目的。张春苗等[16]将FCR模型应用于低碳选址—路径问题(Low-Carbon Location-Routing Problem, LCLRP)，验证了FCR模型在节能减排上的有效性。本文设计了混合量子进化算法(Quantum Evolutionary Algorithm, QEA)，探讨配送中心碳排放对车辆碳排放和配送成本的影响。然而，据笔者所知，目前LCLRPSPD未获得任何研究人员的关注。

LCLRPSPD为NP-hard问题，目前尚未有任何启发式算法(包括超启发式算法)和精确算法求解LCLRPSPD。本文采用量子超启发式算法求解LCLRPSPD，将基于滑动窗口的量子旋转门机制(Quantum Strategies Based Sliding Windows, QSSW)作为高层学习策略用于搜索LLH构成的空间，并监测LLHs最近历史性能而非全局历史性能，SW采取先进先出(First-In-First-Out, FIFO)机制排除不相关的算子早期性能并记录近期的LLHs的性能信息。从仿真实验结果验证了基于QSSW策略求解LCLRPSPD比QS(Quantum Strategies)性能和效率更优。

本文的主要贡献与创新如下：①构造了能够保证解的可行性的编码方式与LLHs，避免了使用解的修复技术；②提出一种快速简单易行的适应度评价方法，避免了适应度的额外计算；③首次将滑动窗口结合量子旋转门更新策略，以实时准确的监控底层算子的近期性能；④建立了一种集成式的三维指数LCLRPSPD模型；⑤首次将超启发式算法用于求解LCLRPSPD。

1 LCLRPSPD 模型

LCLRPSPD可以定义为在一个有M个候选仓库、N位客户和K辆可用配送车辆的完全定向网络中，每个客户均有配货和集货需求，车辆从仓库出发，依次服务一系列客户，同时满足客户的配集货需求后返回起始仓库。求解的问题为在配送过程产生的碳排放量最小的情形下，确定最佳的仓库位置和数量及行车路线。在此，问题的目标包括仓库的固定碳排放和车辆行驶过程造成的碳排放量。

本文参考文献[8，10]，借鉴CLRPSPD和LCLRP的数学模型，给出LCLRPSPD需满足的约束条件：①每个客户节点只能被一个仓库与车辆服务一次；②车辆必须返回起始仓库；③每两节点间弧段上的车辆的负载不能超过额定容量；④仓库的负载不能超过其额定容量；⑤不考虑陆续不定发车情况等等。模型中出现的符号变量含义如表1所示。

表1 参数符号含义

LCLRPSPD数学模型如下：

(1)

(2)

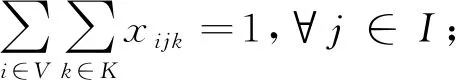
(3)

(4)

xijk=0,∀k∈K,i,j∈J；

(5)

(6)

(7)

(8)

(9)

zij≤yj,∀j∈J,i∈I；

(10)

(11)

(12)

(13)

(14)

(15)

(16)

0≤Qijk≤CV,∀i,j∈V,k∈K。

(17)

其中：式(1)为目标函数或适应度，表示仓库的固定碳排放与车辆运输过程中产生的碳排放的总和；式(2)为FCR模型；式(3)表示客户只能被车辆服务一次；式(4)保证一条路线只能由一辆车服务；式(5)保证仓库之间不能存在任何线路；式(6)表示车辆进出平衡约束；式(7)避免路线中的支路，S为车辆k服务路线的客户集合；式(8)保证每个客户必须由某个仓库服务且只能被其服务一次；式(9)～式(12)表示启用的仓库必须服务客户；式(13)为仓库负载约束；式(14)表示车辆从仓库出发时的负载量，式(15)表示车辆返程时的负载量；式(16)保证车辆在任意弧段上的负载进出平衡等式；式(17)为车辆负载约束。

2 超启发式算法设计

超启发式算法(Hyper-Heuristics, HH)是由Cowling等[19]于2000年提出的一种新型方法论，将其定义为“启发式选择启发式”算法。后来，Burke[20]等拓展了超启发式算法：启发式选择和启发式生成。超启发式算法采用领域屏障隔离高层控制策略(High-level Heuristic, HLH)和底层问题领域层(Low-level Heuristic, LLH)。底层问题领域包含实际问题的数据信息、用于直接搜索问题空间的底层算子以及问题领域的种群信息(染色体和适应度等)。在高层控制域中，存在两种不同目标的策略：算子的选择策略和解的接收机制。选择策略用于搜索LLH构成的空间并监测LLH的历史性能信息以选择优质合适的算子(隔离与任何实际问题相关的任何信息)，而接收准则根据子代解的质量来判断是否取代父代解，控制着算法的搜索方向和收敛速度。此外，在高层控制策略和底层问题领域之间存在信息传递器，用于交换和传递与问题领域无关的信息，包括选择信息、接收策略的判断信息以及底层提供的改进率、算子运行时间与次数、当前解连续无法改进的次数等。

下面将从以下4个方面研究LCLRPSPD和超启发算法：①解的编码与初始解的构造；②超启发算法高层策略的设计，包括2种选择策略和4种接收准则等；③算子库的设计，包括6种局部搜索算子和7种变异算子；④超启发式算法的复杂度分析等。

2.1 解的编码与初始解的产生

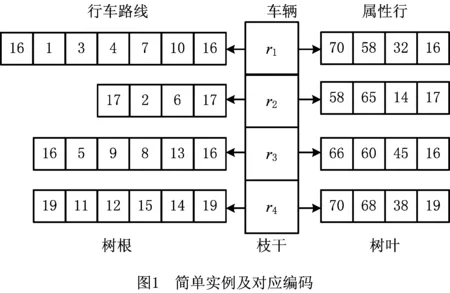
在问题邻域中，一个完整的解可表示为所有路线的集合，即R={r1,r2,…,rK}。每条车辆行驶路线ri的首末两端为所选用的仓库，中间部分为客户节点的编号(表示访问顺序)，且每条路线储存在对应的元胞数组中。染色体长度是仅与车辆数K和客户规模N相关的非定长自然数列，取值为2K+N，元胞数组的长度为K(车辆数是可变的)。此外，为便于快速计算适应度，每条车辆行驶路线的属性也包括在R中(储存在第二行的元胞数组中)，定义为路线属性行，例如：车辆的起始负载、行驶路线的碳排放量以及选用的仓库等等，计算适应度值时只需调用属性行中的路线造成的碳排放与仓库的固定碳排放，避免了重复计算。此外，该编码能够保证路线的可行性且避免了可行性修复技术，减少了计算负担。图1为一个简单实例，即客户集I∈{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}，仓库集J∈{16,17,18,19}，CV=70。类似于分层树形编码方法[8]，树根部分为行车路线，包含4条路线；枝干为车辆数，包含4辆服务车辆即元胞数组的长度；树叶为每条路线的属性，包括起止车辆负载量、碳排放量以及仓库等。

本文的超启发式算法采用单点搜索框架(Single-Point Search Framework, SPSF)，即非种群机制。为了避免SPSF易陷入局部解的特性，每次独立运行的个体从种群中随机选择。本文采用随机生成式方法构建初始种群，即首先随机生成客户序列，利用贪婪法则分配客户并派送车辆(每两节点之间车辆负载必须满足该车辆的容量约束要求)，然后根据形成的车辆路线随机选择仓库(必须满足仓库的容量约束)，并计算每条路线的属性，最后构造完整的车辆路线集。

2.2高层策略构造

2.2.1 QSSW选择策略

在量子计算中，量子位为最小的信息储存单元，可通过量子旋转门实现转变其所处转态(0或1)。鉴于此，超启发底层算子的选择概率更新过程类似于量子位状态的更新机制。在本文的QSSW选择策略中，一个量子位表征为一个LLH，一个长度为|ξ|的量子染色体表示为：

(18)

其中[αi,βi]T为第i个量子位或底层算子的概率幅。|α|2为量子位处于“0”态的概率(算子弃用概率)，|β|2为量子位处于“1”态的概率(算子选择概率)，两者满足|α|2+|β|2=1。在启发式搜索空间的初始化过程中，每个算子的αi与βi的初始值相等，表示所有的LLHs有相等的概率被选择或弃用。

基于量子旋转门的学习策略用于更新与转移量子位或LLH的状态，经由量子门引导个体进化：

(19)

式中：μ为旋转方向，保证算法的收敛，即当底层算子hi在第一、三象限，取值为-1，否则为1；θi为每个量子位的旋转角，控制量子位的选择概率，其值查表获得。为了将底层算子的性能参数反应到旋转角上，采用以下方式计算旋转角的大小：

(20)

(21)

式中，C为常数；pf和cf分别为父代和子代适应度；FRR为FIR标准化后的数值；FIR表示累计适应度改进率(Fitness Improvement Rate, FIR)，当FIR取值为算子全局历史性能时，将采用这种策略的超启发式算法命为HH-QS。然而，现阶段的底层算子的性能可能与算子的早期性能参数不相关，采用全局历史性能作为底层算子的性能表征可能会导致选择不恰当的LLH，因此本文借鉴FRR-MAB[21]中的滑动窗口机制记录算子近期性能，以便改进HH-QS。滑动窗口由W×2维矩阵，第一列为算子使用顺序，第二列为算子的FIR，采用FIFO机制排除滑动窗口中的算子的早期性能参数。最后将滑动窗口中的FIR标准化获得信用分配值，即FRR，命为HH-QSSW。

最后，采用轮盘赌的方式分配算子选择概率hp，可定义为式(22)：

(22)

采用该方法可避免算法后期选择的单一性，增强选择的多样性。

2.2.2 接收准则设计

接收准则(Acceptance)用于判断子代解cf是否替换父代解pf，其处理的好坏直接影响超启发算法收敛速度与优化精度。

当cf优于pf，cf直接取代父本进入下一次迭代，否则利用概率公式(24)计算cf取代pf的概率并做出抉择，查阅文献，几乎所有的接收准则都是一种计算概率p的策略，本文采用4种接受准则：

(1)全接收(AM) 所有的cf都接收并代替pf，即p=1；

(2)蒙特卡洛(MC) 非改进解以概率p=e-δ大小被接收，其中δ=m×Δf/Q，m为常数(本文取10)，Δf=cf-pf，Q为当前解未被改进的计数器，如果最小碳排放被更新，重置Q为ε(无穷小值)；

(3)大洪水(GD) 如果非改进解cf的值小于等于pf+ΔF×(1-t/tmax)时才会被接收，此时p=1，t为当前迭代次数，tmax为最大迭代次数，ΔF=bf1-bft为最大门槛高度，其中bf1，bft分别为第一次迭代最优解和当前迭代最优解；

(4)模拟退火(SA) 非改进解以概率p=e-δ大小被接收，其中δ=(cf-pf)/(ΔF×(1-t/tmax))。

2.3 底层算子设计

底层算子库(Pool of LLH, PLLH)可直接搜索问题领域解空间，由问题领域专家提供。PLLH可视为无法操作的黑箱，根据优化性质分为变异算子和局部优化算子两类。变异算子往往对当前解微小扰动，以便在搜索过程中提供足够的随机性并防止陷入局部最优解，但无法保证获得高质量解。然而，局部优化算子的目的在于改进当前解，促使算法快速收敛并提高收敛精度。这两类算子在组合优化中是必不可少的，本文共构造6种局部优化算子和7种变异算子。

局部优化算子有：线路内部2-Opt(Inside-2opt)、线路间2-Opt(Inter-2opt)、线路内交换客户(Inside-swap)、线路间交换客户(Inter-swap)、线路内移动客户(Inside-shift)和线路间移动客户(Inter-shift)。局部优化算子每次执行的约束条件包括：①改进率FIR≥0；②任意弧段的车辆负载必须小于额定容量；③仓库的负载不能超过额定容量。对于线路内部局部优化时，采用的策略为完全优化策略[22]，而线路间的局部优化则采用K-1优化机制，即随机选定一条路线，与其他路线的客户逐一局部优化，算子复杂度从K(K-1)/2降低为K-1。

变异算子分为两类：一类为针对行车路线扰动的变异算子，包括Inside-2opt-M、Inside-oropt、Inter-shift-M、inter-swap-M和Shaw[23]，这类算子的扰动机制为随机选取1/4～1/2的路线并随机扰动线路内或线路间的客户，并不保证获得优质解；另一类变异算子对仓库进行扰动，包括Add和Relocation。Add算子随机选取1/3～2/3的路线并分配给一个新的仓库或关闭一个仓库，并将该仓库的所有路线安排到另一仓库，以防止过少的仓库导致过快收敛。Relocation将每条行驶路线坍塌为一个“Super-client”，然后将仓库插入到每条路线中获得最小插入成本并作为该仓库与该路线之间的距离，类似于Barreto[24]。变异算子的约束条件为仓库和车辆的负载不能超过额定容量。底层算子库中的所有算子必须满足所有约束条件后才操作，保证路线的可行性和避免使用修复技术。

2.4 算法复杂度分析

算法的时间复杂度是运行时间的相对量度，用于衡量一个算法的运行时间性能。对于种群规模为|P|，迭代次数为Tmax，客户数为N，车辆数为K与底层算子数为NL的问题，迭代一次的算法复杂度如下：高层选择策略中，计算FIR的复杂度为O(|P|)，更新滑动窗口计算复杂度为O(2×W)，计算FRR、旋转门更新以及轮盘赌的复杂度为O(3×NL)，接收策略的复杂度为O(|P|)，精英保留策略的复杂度为O(|P|)。由于无法确定每次迭代的底层算子，计算复杂度设定为耗时最长的算子的计算复杂度即O(|P|×N2)，此外，主循环外部存在种群初始化的计算复杂度为O(|P|×N2)以及适应度计算的计算复杂度O(|P|),算法在迭代一次的计算复杂度约为O(3×|P|)+O(2×W)+O(3×NL2)+O(|P|×N2)，算法的总体计算复杂度O(HH-QSSW)为：

O(HH-QSSW)=Tmax×(O(3×|P|)+

O(2×W)+O(3×NL)+O(|P|×N2))+

O(|P|×N2)+O(|P|)=O((3×Tmax+1)×

|P|)+O(2×WTmax)+O(3×Tmax×NL)+

O((Tmax+1)×|P|×N2)。

(23)

由上述分析可知，算法的整体计算复杂度约为Tmax|P|O(N2)，即高层策略的计算复杂度可忽略不计，HH-QSSW的总体计算复杂度约为底层算子的计算复杂度的总和。

3 仿真实验与比较

实验主要分为3部分，实验1通过与目前求解LCLRP的算法进行对比分析来验证本文高层策略和底层算子的有效性，然后通过实验2确定性能最好的4种策略组合，最后将实验2中的4种组合策略用于求解LCLRPSPD，进一步验证所提的QSSW的高效性与鲁棒性。超启发式算法采用MATLAB 2015b并行编程，计算机环境为intel(R)Core(TM)CPU i7-6700K @4.00 GHz,8 GB RAM, Windows 10。为了保证对比公平性，每个策略组合的算法的终止条件为最大Tmax且采用同一初始种群。此外，每种策略(CF和FRR-MAB)的参数尽量采用文献中参数或随机数的方式，具体参数设置如表2所示。

表2 算法参数设置

3.1 测试算例

目前尚无对低碳LRPSPD的标准算例，为了测试HH-QSSW的性能以及确定最佳策略组合，实验1采用文献[16]改进的Prins算例[27]求解LCLRP，以检验算法的效率和模型的正确性；实验2采用的实例为Barreto标准算例(文献[9])，以确定4种最佳组合策略；实验3改进3类算例以适用于LCLRPSPD，包括Barreto、Prins和Tuzun[28]标准算例。Tuzun标准算例为首次用于求解LRPSPD/LCLRPSPD的算例，所采用的分割方法为Karaoglan方法[29]，且令β=0.8。所有LCLRPSPD原型算例(即LRP标准算例)可从网址http://sweet.ua.pt/sbarreto/private/SergioBarretoHomePage.htm和http://prodhonc.free.fr/homepage上下载。

3.2 仿真实验

3.2.1 分析算法有效性

采用HH-QSSW-SA和HH-SR-SA求解LCLRP，采用的算例为文献[16]改进的Prins算例，结果如表3所示。其中：BKS为已知最小油耗量(单位：L)，由文献[16]获得，BF、MF、SD以及MT分别为最小碳排放、平均碳排放量、标准差以及平均运行时间(s)，Gap表示BF与BKS百分比差距，表格的末尾为所有数据的平均值和中位数。由表3可知，两种策略组合的BF均优于文献[16]中提供的最小碳排放，其中两种策略组合比BKS最多可减少30%碳排放量，最少能降低2%的碳排放量，表明本文算法在降低碳排放量上的有效性和性能优于文献[16]的QEA。此外，在相同的接收准则(SA)下，QSSW的综合性能优于SR，主要表现在BF、MF、SD和Gap的平均值与中位数上，然而QSSW的时间性能劣于SR大约32%，SR算法花费的最大运行时间为236 s，而QSSW策略耗费的运行时间最大为477 s，这符合于No-free-lunch定理[30]。采用Friedman检验(见2.2.4节)对表3的BF统计分析，统计结果见表4，根据统计量p值可推断3种算法之间存在显著差异。表5为Post-hoc Wilcoxon Rank-Sum检验，结论表明HH-QSSW-SA与HH-SR-SA在性能上都优越于QEA。

综上所述，本文提出的超启发式算法能够在合理的计算时间内求解LCLRP并能够获得优质解，表明EHH的高层选择策略和接收准则以及底层算子的有效性。

3.2.2 最佳策略组合选择

3.2.1节分析了超启发式算法在求解LCLRP方面的有效性，本节研究20种组合策略的综合性能以确定4种最佳策略组合用于求解LCLRPSPD问题，其中选择策略有SR、FRR-MAB、CF、QS以及QSSW，接收机制为MC、DG、SA和AM。此外，采用CHESC-Cross-domain heuristic search challenge评分系统(http://www.asap.cs.nott.ac. uk/external/chesc2011/)对20种策略组合进行评分排名，即将适应度从小到大依次排列并赋值前8位组合策略得分(10,8,6,5,4,3,2,1)，其他策略为0分。在Barreto标准数据中，选用了16组实例(客户数N∈[21,150])，即每个策略组合所得最大分为160分，实验结果如表6所示。不考虑接收准则的影响，本文提出的QSSW得分排名第一，SR、QS和FRR-MAB分别列为第二、三、四名，CF表现最差；仅对接收准则分析，GD性能最好排名第一，MC获得344分排名第二，SA与AM性能最差；根据对20种组合策略的综合评分，所选取的4种性能最好的策略为SR-GD、QSSW-MC、FRR-MAB-GD与QS-GD。本文提出的两种算法表现较好，分别以95和83分排第二、四名，SR-GD以112位列第一，FRR-MAB-GD以84分排名第三。从获得满分10分的次数来看，FRR-MAB与SR获得10次，QSSW获得8次，QS获得6次和CF仅获得4次。

表3 LCLRP算例对比

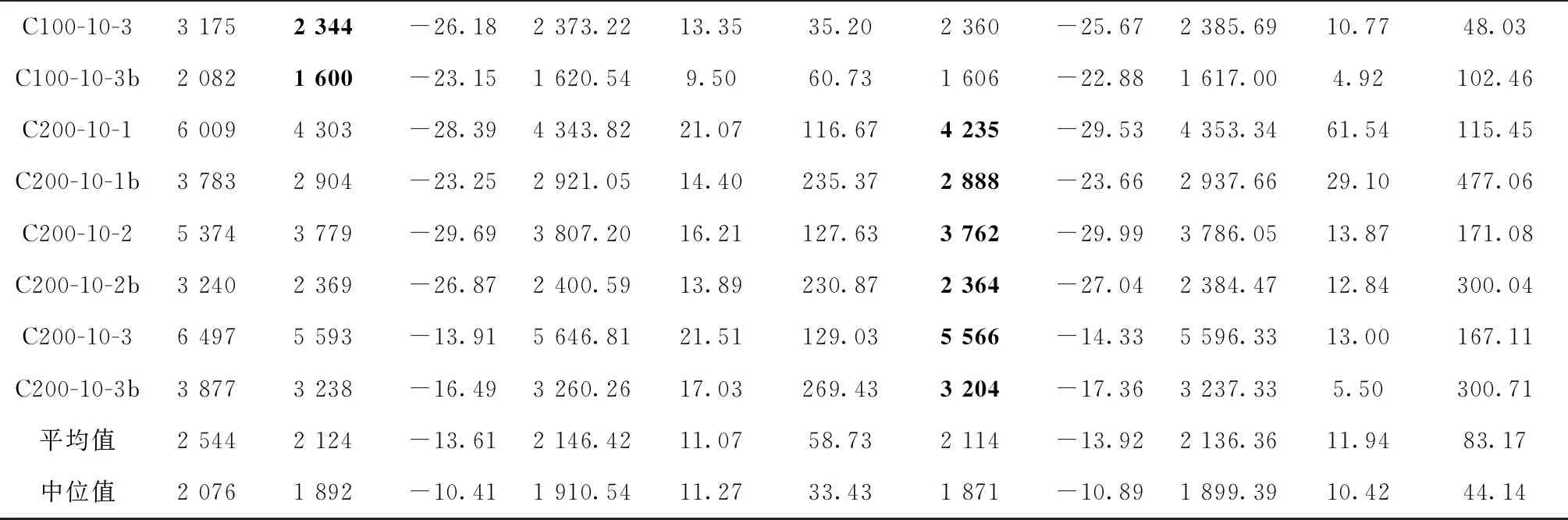
续表3

表4 Friedman统计分析结果

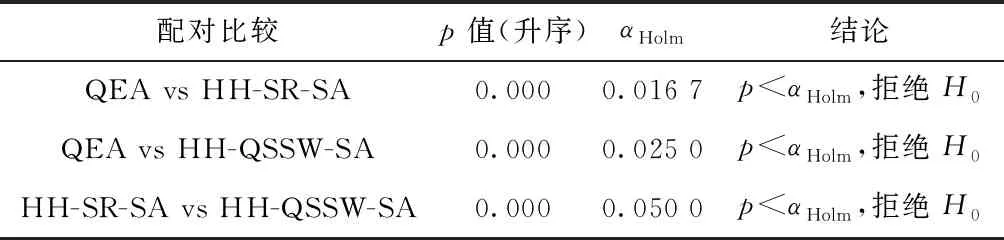
表5 Post-hoc Wilcoxon Rank-Sum统计分析(源自表3数据)

表6 20种组合策略得分

综上所述，本文提出的QSSW以及QS在求解LCLRPSPD表现出较好的性能，SR与FRR-MAB的性能更优。根据评分排名，选用SR-GD、QSSW-MC、FRR-MAB-GD与QS-GD等4种策略组合来执行实验3。

3.2.3 三种算例的求解和模型有效性

本节将实验2的4种精英组合策略用于求解LCLRPSPD的标准实例(Cm≠0)，实验结果如表7～表9所示。类似于表3，仅提供了每个实例的BF和MT(页面空间问题)，此外，由于本文为首次求解LCLRPSPD，无法获得BKS。表格最后一行添加了NB，表示在所获得最小碳排放的个数(粗体表示结果为最小碳排放)。表格的最后两列为所求解的CLRPSPD最小成本模型下的路径规划的碳排放量，其中dif(%)为求解CLRSPD的BF与前4种组合策略所求解的最小BF之间的百分比差距。

表7 Barreto标准实例计算结果

续表7

由表7中4种策略对Barreto的16个算例的运行结果可知，QSSW-MC在16个算例中10次获得最优，FRR-MAB-GD获得9次最优排名第二，SR-GD与QS-GD分别获得6次和4次；就最优值的平均耗油量而言，QSSW-MC以平均值为15552.9位列第一，QS-GD与SR-GD排名第二、三名，FRR-MAB-GD表现最差；SR-GD和FRR-MAB-GD在运行时间上分别为52秒和65秒位列第一、二名，本文的两种策略组合排名最后。此外，QS-GD在求解小规模问题表现出优越的性能，而在大中规模的性能略低于FRR-MAB-GD，与SR-GD持平，但优越于QS-GD。

表8是本文算法求解Prins标准数据的数据结果。在求得最小碳排放个数上，QSSW-MC获得了17次最优，SR-GD和QS-GD分别获得11次和12次，FRR-MAB-GD表现最差只获得了6次最优值，QSSW-MC在大部分规模算例中都能够获得最小碳排放；在最小碳排放的平均值上，QSSW-MC以均值4552.7kg排名第一，SR-GD排名第二，QS-GD和FRR-MAB-GD为末两位。在平均运行时间上，SR-GD和FRR-MAB-GD以63.9 s和76.3 s摘得一、二名，本文的两种策略排名末两位，分别为89.1 s和96.9 s。QSSW-GD在求解不同规模测试问题的性能表现为出现显著差异，且均优越于其他3类。

用4种组合策略求解Tuzun标准算例，求解结果如表9所示。Tuzun标准算例有36个实例，客户数N∈{100、150、200}，仓库为M∈{10、20}，车辆容量为150。QSSW-MC在最小碳排放的平均值和数量排名第一，分别为5212.2kg和16个，SR在最小碳排放平均值和数量上优于FRR-MAB和QS，排名第二，而QS在最小碳排放的数量上优于FRR-MAB但最小碳排放平均值劣于FRR-MAB。此外，对于时间性能，SR-GD和FRR-MAB-GD位列一、二名，本文两种策略排名末位，符合没有免费的午餐定理(no-free-lunch)。

由表7～表9中所求解CLRPSPD的BF和dif.值可知，本文模型在分别求解3类标准实例时可平均降低12.87%、7.05%和9.18%碳排放量，在求解所有算例可平均减少9.14%碳排放量，足以表明本文模型的有效性，可为相关政府部门节能减排政策的制定提供有价值的参考和借鉴。此外，QSSW-MC可获得43个最优解(占所有测试实例52.44%)，相比于QS-GD的占比(约28.05%)提高了24个百分点，即可推断融入滑动时间窗的量子选择策略可大大提供底层算子的选择正确率。相比于SR和FRR-MAB，QSSW能获得最优解的个数提高了21.95%和28.05%，表明QSSW算法的性能有效性和优越性均高于SR和FRR-MAB。

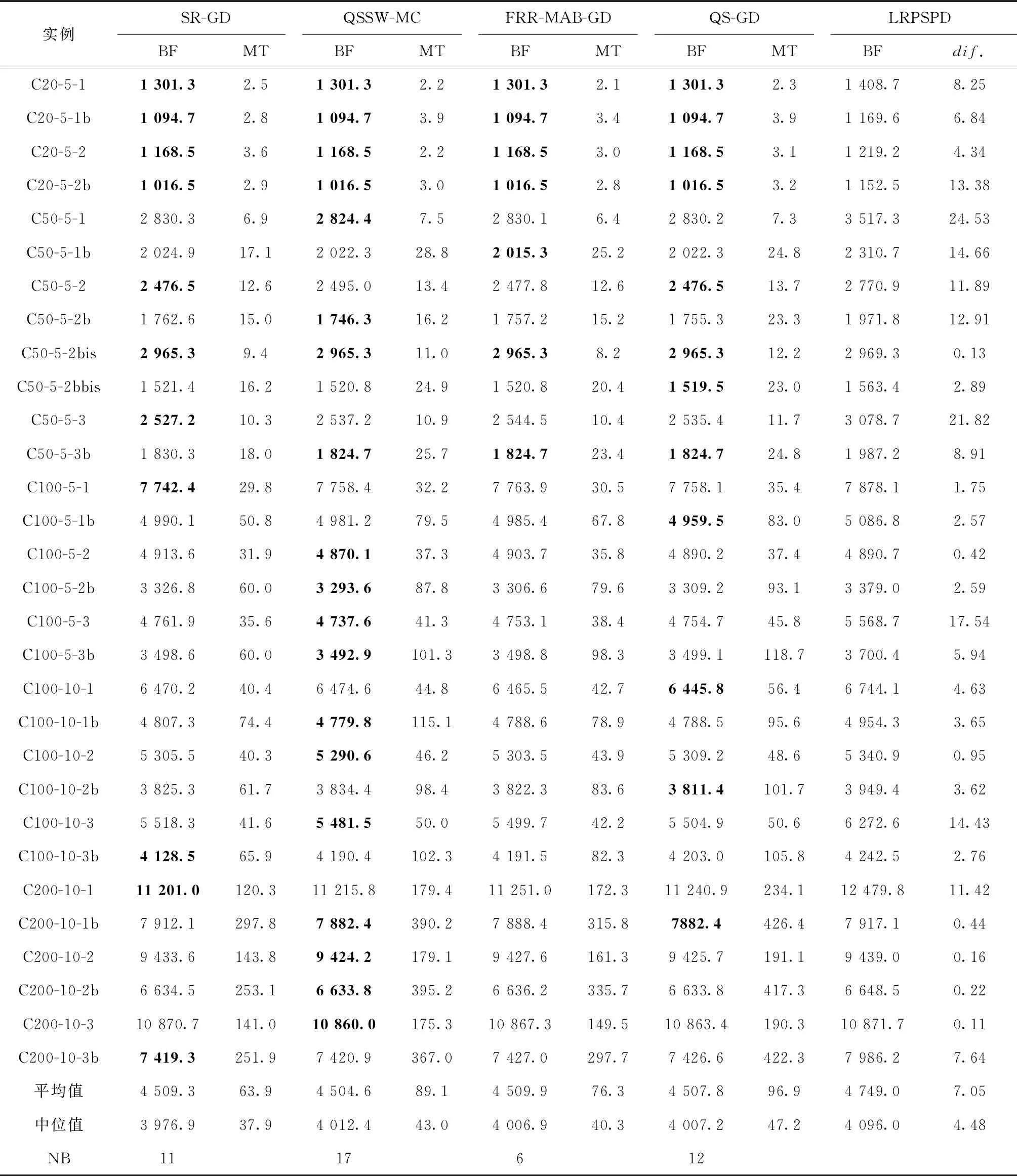
表8 Prins标准实例计算结果

表9 Tuzun标准实例计算结果

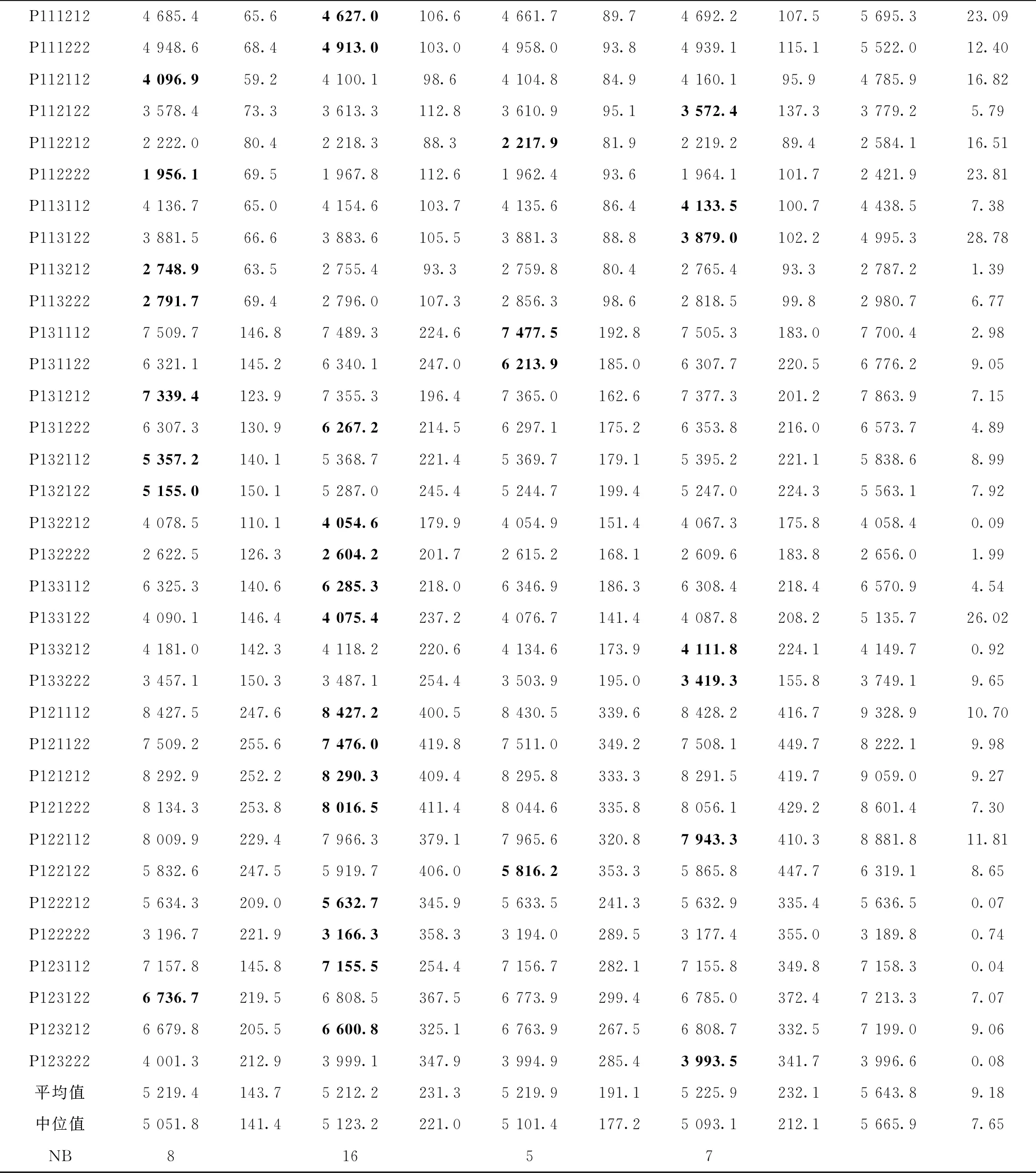
续表9

3.2.4 统计分析

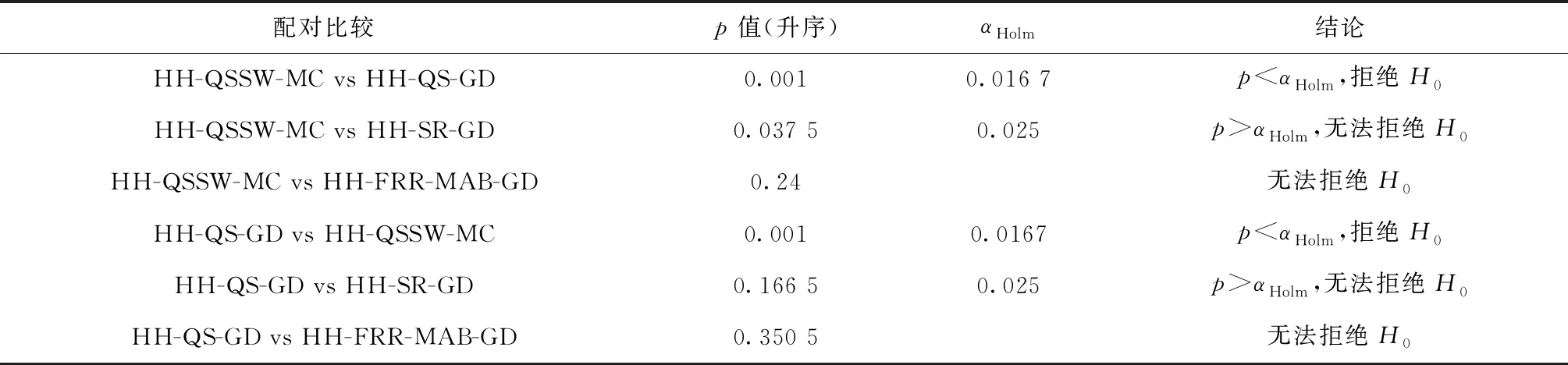
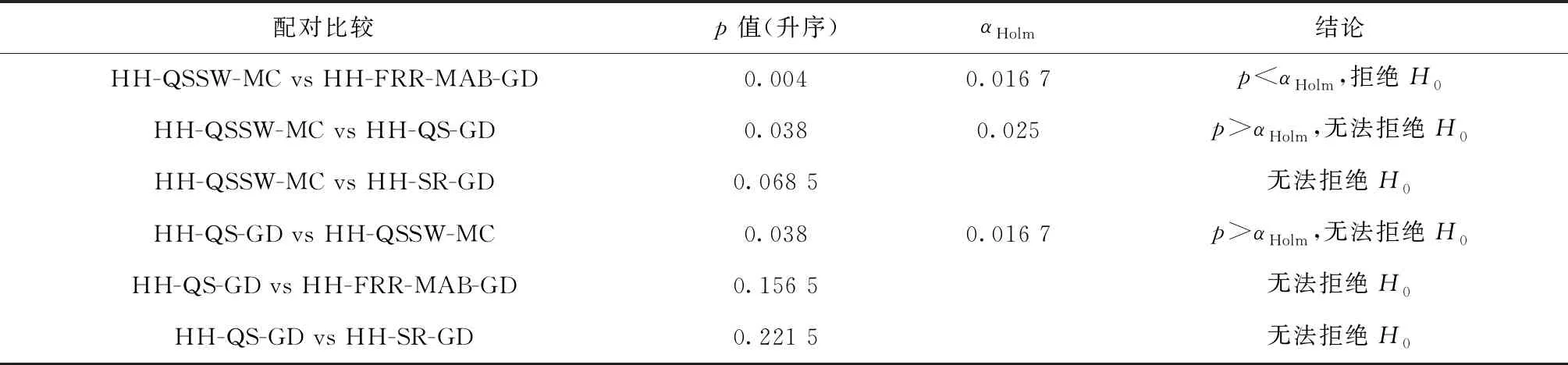
本文对表7～表9的数据结果采用Friedman按秩二因素ANOVA(k样本)统计分析，多重比较的置信水平为95%(即α=0.05)，以检验4种策略组合之间是否存在显著差异，其原假设H0为：多个配对样本来自的多个总体分布无显著差异，即如果Freidman检验统计量χ2大于关键值(查卡方表)，则接收H0,否则拒绝H0，或者如果统计值p值满足p≥α，则接收H0,否则拒绝H0。如果H0被拒绝，事后检验(Post-hoc)采用单边Wilcoxon Rank-Sum检验两两之间是否存在显著差异，其原假设为两个样本中位数相同。为了控制Friedman检验的多重比较谬误(Type I-Family Wise Error Rate, FWER)，采用Bonfeeroni-Holm修正方法修正α值，即首先将p值按升序排列(p1

(25)

按照p值从小到大的顺序依次与式(25)的α值比较，直到pi>αi结束，并保持原假设。统计实验采用IBM SPSS Statistics 19进行，实验结果如表10～表12所示。

将表7中4种策略组合计算结果采用Friedman检验(如表10)，表明4种策略之间存在显著差异。由表11的post-hoc检验结果表明HH-QSSW-MC与HH-QS-GD之间中位数存在显著差异，表明结合滑动窗口的QSSW性能要显著优于QS，然而无法断定显著优于其他两种策略。

对表8中的数据结果采用Friedman检验，结果如表10所示，表明4种策略在获得最小碳排放时存在显著的差异。事后检验结果如表12所示，结果显示QSSW-MC和QS-GD(或SR-GD)之间中位值统计相同，QSSW-MC在性能上显著优于FRR-MAB-GD，此外，无法确定QS-GD与其他策略彼此的优越性。

对Tuzun标准数据的数据结果采用Freidman检验，结果如表10所示。统计量p值为0.272，大于α，表明4种组合策略在求解Tuzun标准实例时不存在显著差异，无法确定彼此的显著优越性。但从最小碳排放的平均值和数量上，可直观地显示QSSW相对其他3个组合的优越性和有效性。

综上所述，QSSW能在合理的计算时间内获得大部分实例的最小碳排放量，可推断出所提算法在求解该算例时的有效性与鲁棒性。此外，对比其他3种组合策略，QSSW在降低碳排放方面表现出巨大的优越性。因此可认为QSSW可实时准确地捕捉底层算子的性能表现并选择合适的算子，以此提高了超启发式算法的框架性能。

表10 Friedman统计分析结果

表11 Post-hoc Wilcoxon Rank-Sum统计分析(源自表7数据)

表12 Post-hoc Wilcoxon Rank-Sum统计分析(源自表8数据)

4 结束语

本文提出一种超启发式算法用于求解LCLRPSPD，优化目标为最小碳排放，包括仓库的固定碳排放与车辆行驶造成的碳排放。首先在问题领域中，建立了符合同时取送货的LCLRP简单明了的三维指数MIP模型；设计了一种满足可行性要求的解编码方式和快速简单的适应度评价方法，以此降低计算负担。其次在超启发式算法设计中，将量子进化算法中的旋转门更新策略作为一种高层学习策略，用于搜索底层算子构成的空间并更新底层算子选择概率以选择算子；然后，将滑动窗口与量子进化策略的高层选择策略相结合，利用算子近期性能信息表征算子的选择概率，真正实现选择的实时性与准确性。

实验部分分为3类。实验1通过对比QEA验证了本文算法在求解LCLRP的有效性与鲁棒性与模型的正确性；实验2采用配对方法对Barreto算例求解并确定了选择策略QSSW-MC、SR-GD、QS-GD和FRR-MAB-GD相比其他组合策略性能最好，接收准则GD和MC相比于AM和SA对算法性能的提高更为明显；实验3通过对3种不同实例(Barreto、Prins与Tuzun标准实例)的仿真、对比和统计分析，表明了实验2的最佳4种组合策略都能有效地求解LCLRPSPD，并且本文提出的QSSW在求解大部分实例的性能表现最好。

未来研究将重点考虑LCLRPSPD与其他实际约束结合，例如：时间窗、多车型等。与此同时，本文的模型仅考虑了距离和载货量对碳排放的影响，其他因素(速度、道路状况、车辆参数等)对碳排放的影响也将会成为未来重点工作之一。此外，尽管QSSW在求解LCLRPSPD时的综合性能较佳，但依旧存在较大的改进空间，下一步将会把QSSW与其他高效的策略结合，例如禁忌搜索、优劣表等[31]。