考虑碳排放的子母穿梭车密集仓储系统复合作业三维路径规划
2020-04-08鲁建厦施贻贯汤洪涛
鲁建厦,施贻贯,汤洪涛,詹 燕
(1.浙江工业大学 机械工程学院,浙江 杭州 310032;2.浙江汇智物流装备技术有限公司,浙江 湖州 313028)
0 引言
密集仓储系统因其自动化程度高、存储率高、占地面积小和空间利用率高等优点,正成为仓储系统建设的主要趋势[1-2]。子母穿梭车(穿梭车集合穿梭板)型密集式仓储系统是一种典型的密集式仓储系统,与传统自动化立体仓库相比,能节省50%~60%的空间[3],但作业效率比自动化立体仓库低,因此如何提升系统运营效率就成为关键问题。
要提高该系统的运营效率,除了需要研究设备选型及货位分配方面的问题外,还要研究子母穿梭车出入库作业的路径优化设计问题。子母穿梭车在执行货物出入库存取任务时,货物存取的方式通常有单一作业方式和复合作业方式两种:①单一作业方式是指子母穿梭车完成单一的出库或入库任务;②复合作业方式是指子母穿梭车执行完入库任务后马上执行出库任务,出库任务与入库任务交叉执行。而为了提高系统的存取效率,子母穿梭车采用复合作业方式进行货物存取。相比于单一作业方式,复合作业的调度更具复杂性,解的搜索空间随着复合作业任务K的增加而增大,可能的路径数目为K!。如何采取合适的复合作业调度策略,在提升子母穿梭车密集仓储系统效率的同时,又能有效的减少出入库设备的碳排放量,很大程度上取决于复合作业三维路径是否合理。因此,研究子母穿梭车密集仓储系统复合作业的三维路径规划方法,如何减少碳排放、提高系统效率成为一个科学问题。
对于自动化立体仓库中出入库设备的复合作业路径优化问题,目前的研究多是以设备运行路径最短或时间最短为目标建立模型。罗键等[4]分析了轨道导引小车系统复合作业任务队列特征,建立了运行时间最短的数学模型,并用改进量子微粒群算法加以优化;杨玮等[5]对堆垛机和有轨穿梭小车(Rail Guided Vehicle, RGV)配置比为1:2的密集仓储系统进行研究,考虑了设备在执行复合作业任务过程中的加速度,建立了以设备运行时间最短为目标的复合作业调度优化模型,并利用混合蚁群算法(Ant Colony System, ACO)进行优化求解;方彦军等[6]针对多RGV和多提升机的自动小车立体仓库系统(Autonomous Vehicle Storage and Retrieval System, AVS/RS)的复合作业调度问题进行研究,建立了以设备完成任务路径最短为目标的数学模型;杨玮等[7]针对双载式多层穿梭车仓储系统复合作业路径优化问题,建立了以最小作业时间为目标的复合作业路径优化模型,在求解该模型时,运用了混合植物繁殖算法,实例证明,该算法能有效减少复合作业调度时间。
对于路径优化中设备的碳排放问题,李进等[8]针对带时间窗的车辆路径问题,在模型中考虑了油耗、碳排放和旅行时间等因素,将车辆速度作为决策变量,建立了以综合成本最低为目标的混合整数规划模型,并提出了两阶段启发式算法对该模型进行求解;潘茜茜等[9]建立了一个考虑碳排放成本的冷链物流配送路径优化数学模型,采用蚁群启发式算法对该模型进行求解;Lerher等[10]研究了小负荷的自动化立体仓库拣选路径规划问题,将拣选过程中出入库设备的能源消耗转化成碳排放量,建立了以设备最小碳排放为目标的能源效率模型,该模型能有效降低设备的能耗,从而降低二氧化碳的排放量;NIA等[11]限制了自动化立体仓库中所有设备的可用时间和允许产生的温室气体总排放量,在拣选路径的模型中考虑了碳排放的税收成本、惩罚成本和折扣成本,建立了以综合碳排放成本最低为目标的拣选路径优化模型,并用蚁群算法对该数学模型进行求解。
综上所述,国外近几年的研究开始在自动化立体仓库出入库设备的路径规划上考虑碳排放因素,而国内对立体仓库复合作业三维路径的规划多是以出入库设备运行路径最短或时间最短为目标建立模型,对出入库设备运行过程中的碳排放因素研究未见相关文献,且模型中并未考虑设备满载与空载的速度差异。以上均未见子母穿梭车系统的碳排放问题的研究。
因此,本文开展对子母穿梭车密集仓储系统复合作业调度(简称密集仓储系统调度)研究,考虑出入库设备空载与满载时的速度差别以及出入库设备在复合作业情况下设备的总碳排放量,建立时间与碳排放成本双目标最优的复合作业三维路径优化模型,并运用混合的智能水滴算法求出该模型的最优解,这将具有重要意义。
1 密集仓储系统调度问题描述与数学建模
子母穿梭车密集仓储系统主要由穿梭母车、穿梭子车、提升机以及货架组成,如图1所示。各穿梭子车轨道存储同种货物,子母穿梭车可通过提升机实现跨层作业,从而实现3个方向运动完全独立,可以最大限度地优化系统效率。同时系统可拓展性强,可通过增加穿梭子车和穿梭母车的数量,解决高峰与低谷出入库作业。

图2为密集仓储系统的简化图,X轴方向表示穿梭母车运动方向,Y轴表示穿梭子车运动方向,Z轴表示提升机运动方向。图中每个格子表示一个货位,各个货位的坐标(x,y,z)对应其货架的排列层。
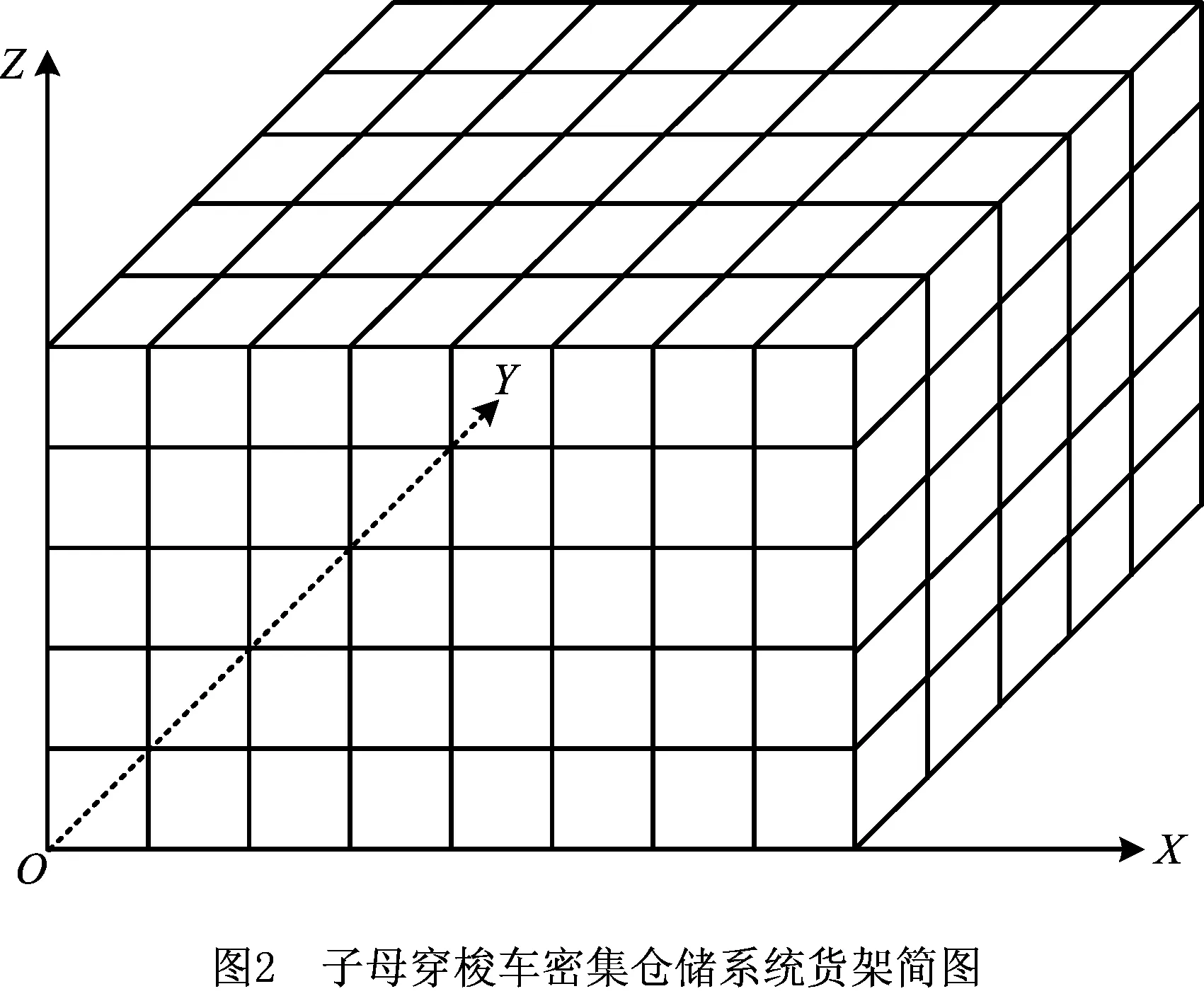
当子母穿梭车执行复合作业时,假设入库货位为A(xi,yi,zi),出库货位为B(xj,yj,zj),则完成一个复合作业需经过入库阶段、空载阶段及出库阶段3个阶段:
(1)入库阶段 提升机结合满载的子母穿梭车沿Z轴方向运行,到达货位A对应的层数(zi)时,子母穿梭车与提升机分离。穿梭母车结合满载的穿梭子车沿X轴方向运行,到达货位A对应的排数(xi)时,由穿梭母车上的车载输送机释放子车。满载的穿梭子车沿Y轴运行,到达货位A所在的位置,完成存储任务(如图3)。
(2)空载阶段 空载的子母穿梭车结合提升机沿Z轴运行到出库货位B对应的层数(zj)时,穿梭子母车与提升机分离。穿梭母车结合空载的穿梭子车沿X轴方向运行,到达货位B对应的排数(xj)时,由穿梭母车上的车载输送机释放子车。子车沿Y轴运行到出库货位B所在的位置(如图3)。
(3)出库阶段 穿梭子车拣选货物后沿Y轴运行到穿梭母车所在的位置,由穿梭母车车载输送机将子车与母车结合,满载的子母穿梭车沿X轴运行到提升机所在的位置。提升机结合满载的子母穿梭车沿Z轴运行至出入库站台,即O点,完成取货任务(如图3)。
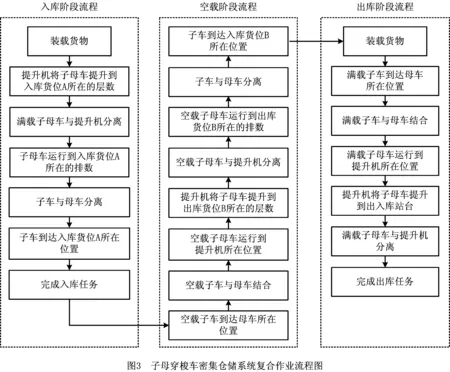
为了对子母穿梭车密集仓储系统复合作业的调度进行研究,作以下假设:
(1)当子母穿梭车执行复合作业时,子母穿梭车每次只能承担一个单位负载的出入库操作,且穿梭车完成任务后停靠在该任务的目的节点,等待下一个任务的分配。
(2)关于出入库设备的复合作业行程时间模型,考虑子母穿梭车满载及空载的速度差异、穿梭母车车载输送机提取满载或空载穿梭子车的时间、穿梭母车车载输送机卸载空载或满载穿梭子车的时间。
(3)关于出入库设备的复合作业碳排放成本模型,考虑了穿梭子车、穿梭母车、母车车载输送机以及提升机的功率,设置一个温室气体(Greenhouse Gas, GHG)的转换系数,并考虑了设备生产1 t温室气体的单位税收成本。
1.1 复合作业行程时间
子母穿梭车密集仓储系统中,出入库设备的复合作业行程时间包括穿梭母车作业时间、穿梭子车作业时间、母车车载输送机作业时间及提升机作业时间。因此可得出密集仓储系统进行第k次复合作业所用的行程时间
Tk=Tmk+Tsk+Tek+Tck。
(1)
式中:Tmk表示第k次复合作业穿梭母车的作业时间;Tsk表示第k次复合作业穿梭子车的作业时间;Tek表示第k次复合作业提升机的作业时间;Tck表示第k次复合作业穿梭母车车载输送机的作业时间。
当系统执行复合作业时,需要考虑以下两种情况:
(1)入库货位和出库货位在同一层时;
(2)入库货位和出库货位在不同层时。
数学模型可表示为
(2)
同时,各出入库设备复合作业中,考虑设备的满载与空载的速度差异,则各出入库设备作业时间为
(3)
(4)

(5)
Tck=2(tc+tc′)。
(6)
式中:坐标(xi,yi,zi)表示第k次复合作业时入库货位的位置;坐标(xj,yj,zj)表示第k次复合作业时出库货位的位置;Vm′表示穿梭母车满载时的平均速度;Vm表示穿梭母车空载时的平均速度;Vs′表示穿梭子车满载时的平均速度;Vs表示穿梭子车空载时的平均速度;Ve表示提升机的平均速度;tc′表示穿梭母车车载输送机提取或卸载满载穿梭子车所需的平均作业时间;tc表示穿梭母车车载输送机提取或卸载空载穿梭子车所需的平均作业时间。
1.2 设备碳排放成本
当密集仓储系统的出入库设备执行第k次复合作业时,所有出入库设备的碳排放成本为
TCk=TEk×Ce=(PCk×fe)×Ce,
(7)
PCk=PCmk+PCsk+PCek+PCck。
(8)
式中,TCk表示第k次复合作业所有出入库设备碳排放的总成本;TEk表示第k次复合作业所有出入库设备碳排放总量;Ce为设备生产1 t温室气体的单位税收成本[12],;PCk表示第k次复合作业所有设备电能总消耗量;fe表示温室气体(GHG)转换系数[12],即以煤电为主的火力发电厂为例,生产1度电产生的二氧化碳量。PCmk、PCsk、PCek以及PCck分别对应着第k次复合作业时穿梭母车、穿梭子车、提升机以及母车车载输送机等设备的电能消耗量:
PCmk=Pm×Tmk,
(9)
PCsk=Ps×Tsk,
(10)
PCek=Pe×Tek,
(11)
PCck=Pc×Tck。
(12)
式中Pm、Ps、Pe、Pc分别对应着穿梭母车、穿梭子车、提升机及母车车载输送机等设备的功率。
1.3 模糊双目标优化
为保证密集仓储系统出入库效率同时减少设备的碳排放成本,本文建立了复合作业行程时间与碳排放成本的双目标优化模型,采用模糊解法对双目标优化问题进行处理[13-14],主要步骤如下:
(1)以设备复合作业行程时间最低为目标进行求解,得到最低时间F1m,求得此时的碳排放成本为F2M。
(2)以碳排放成本最低为目标进行求解,得到最低碳排放成本为F2m,求得此时的行程时间为F1M。
(3)对时间与成本的目标函数进行模糊化处理,建立由单目标函数值到隶属度的映射。本文采用线性规划规则的隶属度函数对子目标函数进行模糊化,则设备复合作业行程时间目标函数值的隶属度为
(13)
碳排放成本目标函数值的隶属度为
(14)
(4)在对时间与成本这两个子目标进行模糊处理后,可定义满意度指标F来表示决策者对调度方案的满意程度,由此将原有的多目标优化问题转变为单目标优化问题,
F=min{μ(f1),μ(f2)}。
(15)
2 密集仓储系统调度算法设计实现
密集仓储系统调度问题属于NP-hard问题[15]。处理NP难问题比较常用的智能优化算法如模拟退火算法(Simulated Annealing,SA)、蚁群算法(Ant Colony Optimization,ACO)、遗传算法(Genetic Algorithm,GA)等。随着智能优化算法的不断发展,如智能水滴算法(Intelligent Water Drops algorithm,IWD)、布谷鸟搜索(Cuckoo Search,CS)算法等智能算法开始运用于解决NP难问题。IWD算法[16]是由Shah-Hosseini于2007年提出来的一种模仿自然界河水和其周围环境的相互作用而形成河道过程的智能优化算法,它已成功解决如旅行商问题[17]、多维背包问题[18]、路径规划问题[19]及作业车间调度问题[20]等组合优化问题。然而,在每次迭代后,IWD只更新最优解集合中的河道泥土量,这在一定程度上限制了算法解的多样性,导致算法陷入局部最优解。CS算法是由Yang[21]于2009年提出的一种模拟布谷鸟的寄生性育雏行为的自然启发式算法,能有效求解最优化问题。CS结构简单,参数较少,有着较强跳出局部最优的能力。
针对IWD前期全局搜索能力较强及算法收敛速度快、CS局部搜索能力强等特点,将两种算法进行结合,提出基于CS作为局部搜索的混合智能水滴算法(The CS as Local Search Hybrid Algorithm,LSHA), Teymourian等[22]验证了LSHA求解有容量约束的车辆路径规划问题(Capacitated Vehicle Routing Problem,CVRP)较其他启发式算法的有效性,CVRP属于NP-hard问题[23],当车辆路径规划问题只有一条路径且没有容量约束时,便是经典的旅行商问题(Traveling Salesman Problem, TSP)[24],因此CVRP可以看做是TSP的拓展,而且CVRP远比TSP复杂,则运用LSHA求解TSP具有有效性,而子母穿梭车密集仓储复合作业三维路径规划问题类似于TSP,故利用LSHA对子母穿梭车密集仓储系统复合作业三维路径规划问题进行求解。
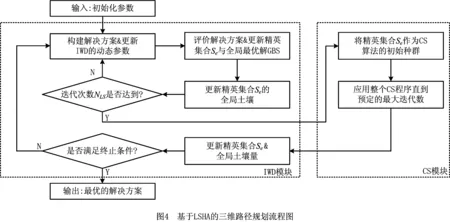
如图4所示为基于LSHA的三维路径规划流程图。LSHA将CS集成到IWD的局部搜索程序中,将IWD全局搜索能力与CS的局部搜索能力相结合,从而寻找出最优的解决方案。该算法主要包括IWD模块和CS模块两个模块。IWD利用全局搜索找到最优解的区域,然后用CS进行局部搜索。在这种混合算法(LSHA)中,核心程序是IWD,其次是利用莱维飞行强化过的CS,并允许算法在早熟收敛时跳出局部最优解。IWD模块通过一些迭代来更新精英集合,然后对这些精英集合进行CS模块来提高搜索质量,进而更新全局的泥土量及精英路径的泥土量。最后,重复IWD算法的主要过程,直到满足终止条件。
2.1 编码方式
基于子母穿梭车密集仓储系统调度模型的特点,采用出入库混合整数编码方式,即编码序号代表货物的编号。假设共有K个复合作业任务,则应包含K个入库任务以及K个出库任务,其中复合作业中某货位坐标若为(0,0,0),表示此时该任务对执行单一出库(入库)作业。将K个入库任务随机编码为1~K,将K个出库任务随机编码为K+1~2K,每个水滴一条完整的路径都代表一个调度方案,且路径中的每个整数编码都代表一个货位,第奇数个的编码为入库货位,第偶数个的编码为出库货位。如智能水滴第k条路径为Xk=(xk1,xk2,xk3,xk4,……,xk(2k-1),xk(2k)),其中xk1、xk3、…、xk(2k-1)为入库货位,xk2、xk4、…、xk(2k)为出库货位。
2.2 适应度函数
假设整个密集仓储系统出入库调度作业由K个复合作业任务组成,在三维路径规划中,所有出入库设备碳排放成本及行程时间最小是算法最后需要达到的目标,则适应度函数为
MinFfitness=Min(-F)。
(16)
2.3 密集仓储系统调度模型LSHA算法流程
步骤1初始化算法参数。包括IWD参数:av,bv,cv,as,bs,cs,ρn,ρIWD,NLS;初始泥土含量ini_soil(i,j);初始水滴速度ini_Vk;智能水滴个数NIWD;最大迭代次数MaxIWD;精英集合Se的大小NSe,以及CS参数:Pa,s;最大迭代次数Maxcs。
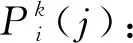
(17)
式中:f(.)是路径上泥土量的相关函数,
(18)
ε是一个非常小的正数,通常ε=0.01;
函数g(.)是用来保证货位i到货位j之间路径的泥土量始终为正数,
g(soil(i,j))=
(19)
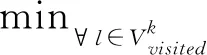
步骤3更新当前水滴速度及泥土含量。第k个水滴在t+1时刻从货位i运动至货位j的速度变换Vk(t+1)表达式为:
(20)
式中:av、bv、cv是初始设定大于0的静态参数。路径中的泥土量
soil(i,j)=(1-ρn)×soil(i,j)-
ρn×Δsoil(i,j),
(21)
Δsoil(i,j)表示路径中被移除的泥土量,
(22)
as、bs、cs是用户选定的大于0的静态参数,time(i,j:Vk(t+1))表示一个水滴从货位i移动到货位j所需要的时间,
(23)
dist(i,j)表示货位i到货位j的距离;ρn为局部泥土更新系数。
步骤4评价解决方案及全局泥土更新。通过适应度函数评估各路径后,构成一个精英路径的集合Se,然后对精英路径进行迭代后得出最优解TSe,设当前全局最优解为GBS,则GBS更新为
(24)
式中q(.)为适应度函数。在每一次IWD算法迭代结束后,根据式(25)对每一条最优路径TSe进行全局泥土量更新
(25)
soilk=soilk+Δsoil(i,j)。
(26)
式中:ρIWD为全局泥土更新系数,d为此次迭代节点数,第k个水滴中的泥土量soilk表达式如式(23)所示。
步骤5CS局部搜索。当迭代次数达到NLS,就应用CS局部搜索模块,将Se作为CS的初始化种群,在Maxcs次迭代中局部改进,布谷鸟寻窝的路径和位置更新如式(27)和式(28)所示,之后按步骤4的公式更新精英集合及全局泥土量,若终止条件不满足,则转至步骤1,否则终止程序,输出最优解。
Xi(t+1)=Xi+α⊕Levy(s,δ),
(27)
Levy(s,δ)~s-δ(1<δ)。
(28)
式中:α>0,为步长大小,⊕表示点对点乘法,Levy(s,δ)为搜索路径,服从莱维分布,s为步长,δ为均匀分布中抽取的一个随机数。
其核心伪代码如下:
算法1Algorithm of LSHA for shuttle combined vehicles three-dimensional path planning。
Begin
1.初始化算法参数;
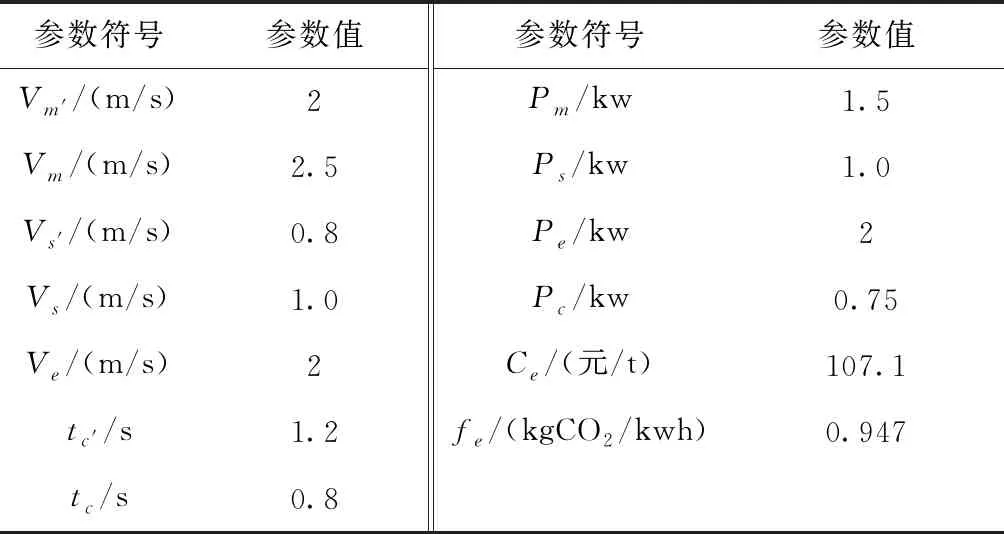
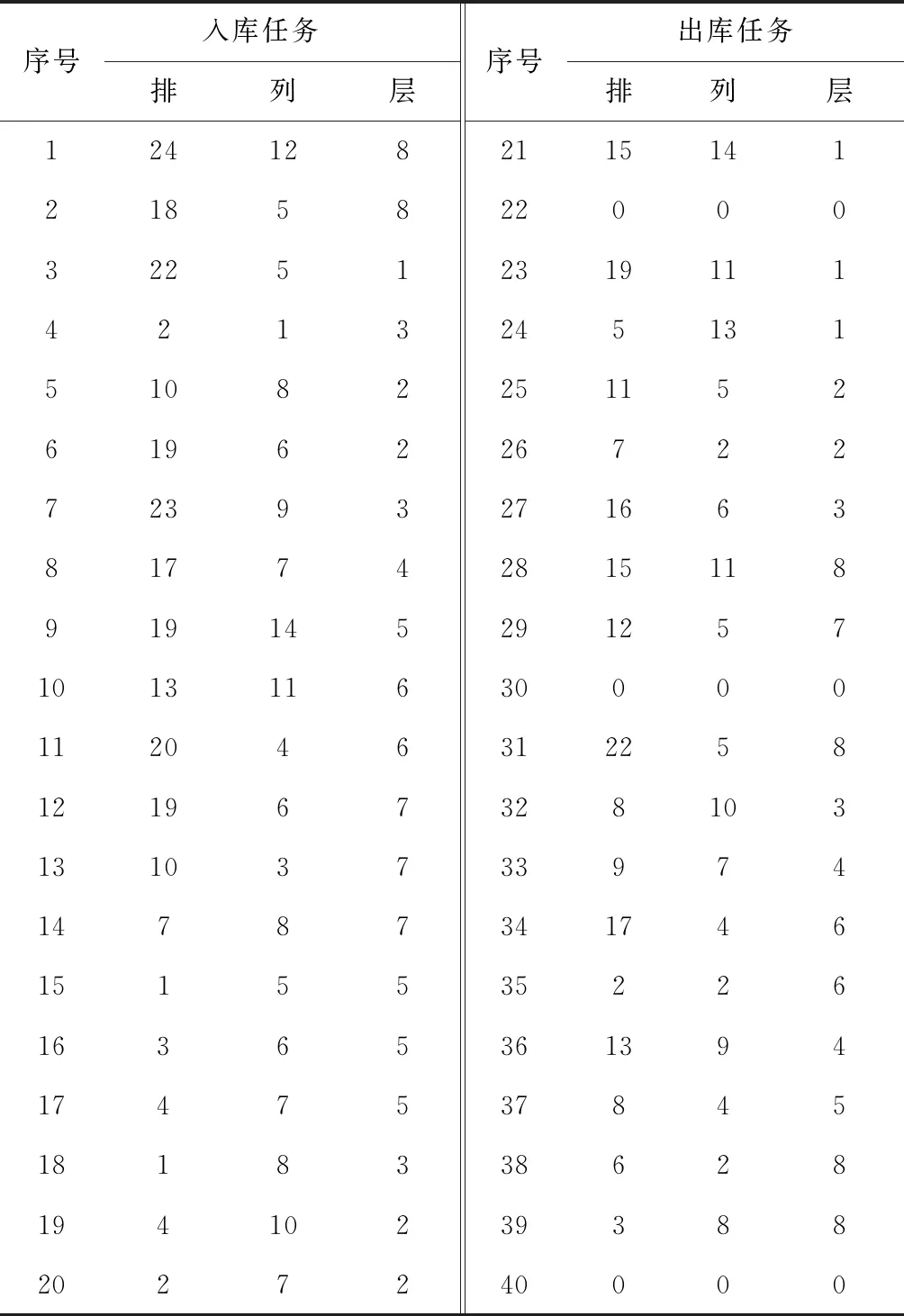
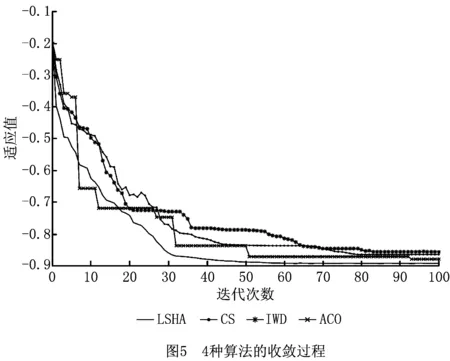
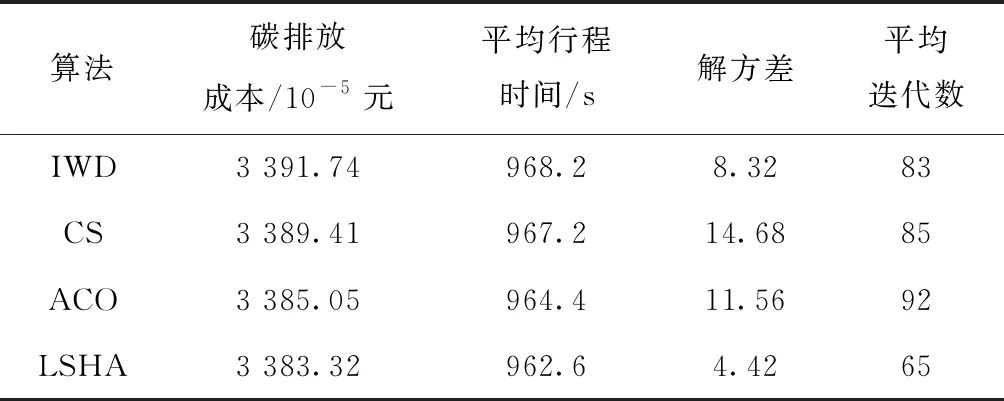
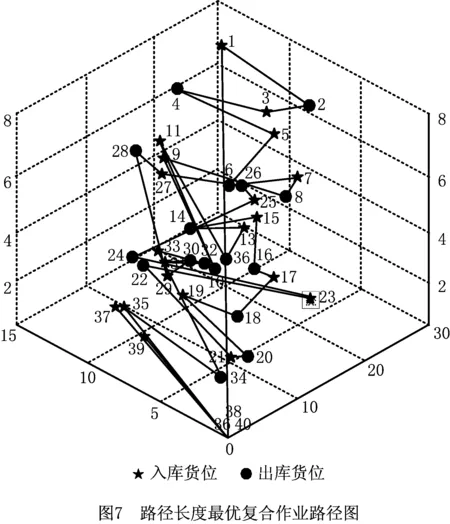
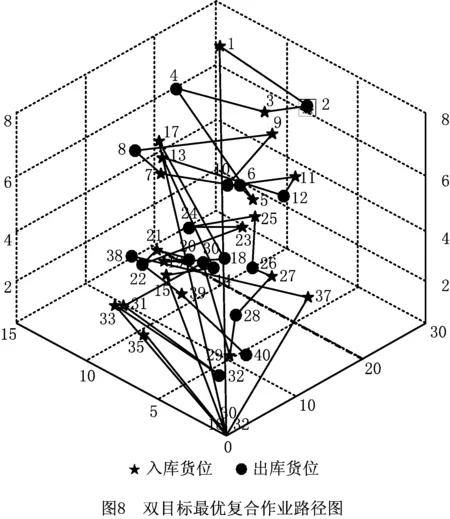
2.while t 3. for NIWD个IWD do 4. 设置货位候选表与货位禁忌表为空; 5. while未构建一个完整的路径do 6. Current node i:=I/O Station; 7. while 复合作业订单中所有货位没有被访问do 9. 选取下一节点(j); 10. 更新水滴速度Vk(t+1); 11. 更新泥土变化量Δsoil(i,j); 12. 更新河道泥土含量soil(i,j); 13. 更新水滴泥土含量soilk; 14. Current node i:=next node j; 15. 更新货位候选及禁忌列表; 16. endwhile 17. endwhile 18. 评价解决方案; 19.endfor 20.更新精英集合最优解TSe; 21.更新全局最优解GBS; 22.for Se中每条路径do 23. 全局泥土更新; 24.endfor 25. If(迭代次数达到NLS) 26. 将Se作为CS的初始化鸟巢xi(i=1,2,…,NSe); 27. while迭代次数 28. 采用莱维飞行随机生成新的解f(xi); 29. 在Se中随机选取一个鸟巢xj; 30. if f(xi)>f(xj) 31. 用新解替换鸟巢xj; 32. endif 33. 按pa丢弃差的鸟巢; 34. 用偏好随机游动产生新的鸟巢; 35. 保留最好的解,完成一次迭代; 36. for Se中每条路径do 37. 全局泥土更新; 38. endfor 39. endwhile 40. endif 41.endwhile 42.可视化结果 End 为了验证LSHA求解复合作业三维路径规划问题的有效性,引用文献[5]中26排14列8层的货架为仿真实验研究对象,单元货位尺寸分别为l=1.2 m,w=0.8 m,h=1 m,以文献[12]中的研究成果为例,即产生每度电时二氧化碳排放量为0.974 kg,每吨二氧化碳的税收成本为107.1元,研究的模型初始参数值如表1所示。 表1 模型初始参数值 随机生成40条目调度任务,出入库货位点如表2所示,分别用LSHA、IWD、CS及ACO对该算例进行试验比较,由于参考文献[22]中Teymourian等验证了LSHA求解有容量约束的车辆路径规划问题的有效性,因此本文中CS、IWD及LSHA中的参数均采用参考文献[22]中的参数,而文献[25]中李孟霖验证了ACO求解TSP问题的最优参数,因此本文ACO参数采用的是文献[25]中的参数。其算法参数如下: ACO[25]:MaxACO=100;蚂蚁数m=19;信息素启发式因子α=1;期望启发因子β=5;信息素挥发系数=0.1;信息素总量Q=100。 IWD[22]:av和as值为1、bv和bs值为0.1、cv和cs值为1;局部土壤更新系数ρn及全局土壤更新系数ρIWD均为0.9;智能水滴个数NIWD=100;最大迭代次数MaxIWD=100;智能水滴初始泥土量ini_soil(i,j)=1000;智能水滴初始速度ini_Vk=100。 CS[22]:Pa=0.9;s=10;最大迭代次数Maxcs=100;种群个数NCS=100。 LSHA[22]:NLS=15;精英集合Se的大小NSe=15。 表2 出入库货位详细表 图5为实例的4种算法采用MATLAB编程,并运算30次的平均收敛过程曲线。可以看出ACO算法搜索能力强,具有较好的搜索解能力,但是算法需要较长的搜索时间,收敛速度慢;IWD算法前期全局搜索能力较强,算法收敛速度快,但局部搜索能力弱,从而导致求解的精度不高;CS算法全局搜索能力较弱,所以前期算法收敛速度较慢,算法后期局部搜索能力强,求解精度较IWD高;而LSHA算法结合CS及IWD这两种算法的优点,充分发挥IWD的全局搜索能力,使得算法前期快速收敛,又结合了CS的局部搜索能力,提高求解精度,使得改进后的算法在收敛速度和求解精度上都有相应的提高。 实例的4种算法独立运行30次后,结果如表3所示。 表3 实验结果 从表中可以看出,ACO算法相对于CS算法及IWD算法来说存在收敛速度慢的缺点;CS算法相对于IWD算法与ACO算法来说存在解波动较大的缺点;IWD算法相对于CS算法及ACO算法来说存在最优解及解平均值较差等缺点。针对IWD算法局部搜索能力差的缺点,结合CS算法局部搜索能力,提出了基于CS算法进行局部搜索的LSHA,相对于其他3种算法,在求解精度、解波动程度及收敛速度上都有一定的提高,更适合本模型的寻优。 利用LSHA进行复合作业货位调度组合和顺序优化,得到在完成40条调度任务的同时双目标模型最优的作业顺序为(24,12,8)—(22,5,8)—(18,5,8)—(15,11,8)—(10,3,7)—(6,2,8)—(7,8,7)—(3,8,8)—(19,6,7)—(12,5,7)—(20,4,6)—(17,4,6)—(13,11,6)—(2,2,6)—(1,5,5)—(0,0,0)—(19,14,5)—(8,4,5)—(3,6,5)—(9,7,4)—(4,7,5)—(8,10,3)—(17,7,4)—(13,9,4)—(23,9,3)—(16,6,3)—(19,6,2)—(11,5,2)—(2,1,3)—(19,11,1)—(1,8,3)—(5,13,1)—(4,10,2)—(0,0,0)—(2,7,2)—(0,0,0)—(22,5,1)—(15,14,1)—(10,8,2)—(7,2,2)。 根据程序随机选取一组复合作业路径顺序(具体路径如图6所示),并与路径长度最优的复合作业路径顺序(具体路径如图7所示)、双目标最优复合作业路径顺序(具体路径如图8所示)相比较,结果如表4所示。 表4 路径对比分析表 复合作业路径总行程距离/m总行程时间/s总碳排放成本/10-5元随机路径1 688.41 127.084 123.49最短路径1 288.4968.283 392.11双目标最优路径1 293.2962.63 383.32 由表4可知,双目标最优复合作业路径相对于随机路径,总行程时间优化了14.6%,总碳排放成本优化了17.9%,同时,相对于最短路径,双目标最优路径在行程时间及碳排放成本上均有一定的降低。因此,LSHA能在保证正常的出入库效率的同时,还能有效的降低设备的碳排放成本,对于企业来说,一方面能有效的提高密集仓储系统的效率,另一方面又能在降低碳排放量的同时减少电能的消耗,降低企业的综合运营成本,具有现实应用意义。 为了提高子母穿梭车密集仓储系统出入库效率,本文开展了对该系统复合作业三维路径问题研究,在建立的模型中考虑了出入库设备的碳排放成本及满载与空载的速度差异,建立了复合作业行程时间与碳排放成本的双目标调度优化模型。针对该问题,设计了LSHA对模型进行求解。实例仿真结果表明,时间与成本的双目标优化模型能有效提高仓储系统效率,减少企业碳排放成本。由于本文在调度模型中只考虑了一台子母穿梭车的情况,出入库效率较低,只适用于小型的密集仓储系统,后续,将对大型的子母穿梭车密集仓储系统进行研究,通过对多台子母穿梭车复合作业路径进行规划,在最大程度上减少企业的碳排放量。3 仿真研究


4 结束语
