多目标斗链式混流拆卸线平衡的Pareto花朵授粉算法
2020-04-08曾艳清张则强刘思璐李云鹏
曾艳清,张则强,张 颖,刘思璐,李云鹏
(西南交通大学 机械工程学院,四川 成都 610031)
0 引言
科技的快速发展加快了产品更新换代的步伐,由此产生了大量的废旧产品。处理废旧产品的主要方式有再制造、再使用和回收。再制造和再使用能够延长产品的使用周期,而废旧产品的拆卸回收能够实现资源能源的再利用,并能够减少废旧产品中有危害物质对生态环境的影响,同时也能够为拆卸企业带来可观的经济效益。拆卸生产线是处理大规模废旧产品的最主要的方式。拆卸线具有高效率、低成本、低污染等优势,已被众多拆卸企业所采用。为进一步提高拆卸线的生产效率,在满足多种生产约束的前提条件下,如何合理地将拆卸任务分配到生产线中,并满足多项生产线指标的优化,依然是一项难题,即拆卸线平衡问题(Disassembly Line Balancing Problem, DLBP)[1]。
现有文献中,一般通过优化工作站内任务分配或是改善生产线布局形式来提高生产线效率。在进行任务分配时要求每个工作站中的负荷尽可能相同,均衡工作站作业时间一直被视为拆卸线平衡问题最主要的优化目标。但拆卸线平衡问题是离散组合优化问题,通过算法优化分配到工作站中任务的方式,并未改变作业不均衡的本质,因为工人被固定在工作站中,加上工人作业效率和作业任务的差异,生产线难以真正实现负荷平衡。
学术界针对生产线不平衡问题的主要研究成果是斗链模型。斗链作为一种生产组织方式,规定工人可以在连续的多个工位中作业。这种作业方式突破了固定工位的限制,工人只需按一定的作业效率排列在生产线上,无需过多干预,生产线最终即可实现自我平衡[2]。因斗链生产组织方式良好的自组织性和自平衡性,已被广泛应用于装配线与快递物流业中[3]。故本文考虑将斗链生产组织方式应用于拆卸线中,以提升拆卸线的平衡性能。
此外,因较多待拆卸产品具有结构和工艺相似的特点,混合品种拆卸线(简称混流拆卸线)受到众多拆卸企业的青睐[4]。混流拆卸线不仅能够提高生产线的利用率,还能够减少生产线建设成本,具有广阔的应用前景。因此,在拆卸线形式上,本文将构建混流拆卸线平衡模型。
拆卸线平衡问题是典型的NP-hard问题[5],因问题约束较复杂,优化目标较多,求解难度较大,学术界求解该问题的出发点是探索高效求解方法,主要包括精确方法、启发式方法和包含群智能算法在内的元启发式方法。如McGovern等[6]、Avikal等[7]均采用启发式方法对拆卸线平衡问题进行求解。虽然启发式方法能够快速得到问题的解,但很难求得最优解。Altekin等[8]通过数学规划法求解以利润为导向的拆卸线平衡问题,并用CPLEX软件求得问题的最优解;Bentaha等[9]提出了随机作业时间的混合整数拆卸线平衡模型,同样采用精确方法进行求解。精确方法能够得到小规模问题的最优解,但在求解大规模问题时难以在合理时间范围内获得满意解。McGovern等利用遗传算法[5]、蚁群算法[10]等元启发式算法对多目标拆卸线平衡问题进行了优化,能够快速获得问题的近优解或满意解。花朵授粉算法作为一种新近提出的元启发式方法,具有参数少、结构简单、局部搜索能力强等优点,在拆卸序列优化和车间调度问题中均表现出较优的求解性能。基于此,本文考虑将花朵授粉算法用于优化拆卸线平衡问题,进一步拓展问题的优化途径。
拆卸线平衡问题是多目标组合优化问题,其优化目标主要包括最小化工位空闲时间、最大化拆卸利润、最小化拆卸危害[5]。文献[7-9,11-12]并未考虑这些优化目标,无法全面准确地评价拆卸线的性能。而文献[5-6,10,13]在求解多目标问题时采用字典顺序法或加权法这类单目标方法进行求解,一次只能得到一个解,无法获得在各个目标上各有侧重的多种平衡方案,丧失了多目标问题解的多样性。丁力平等[14]采用基于Pareto支配关系的多目标蚁群算法优化拆卸线平衡问题,能够得到多个较优方案。在此基础上,张则强课题组采用拥挤距离筛选非劣解的精英保留策略进一步提高了多目标元启发式方法的求解性能[15-19]。借鉴上述多目标优化方法,本文将设计多目标花朵授粉算法对多目标斗链式混流拆卸线平衡问题进行优化。
综上所述,本文考虑在混流拆卸线中实施斗链生产组织方式,建立多目标斗链式混流拆卸线平衡模型,同时构造基于Pareto支配关系的多目标花朵授粉算法,设计结合问题特征的算法策略,并验证模型和算法的性能,以及分析斗链式混流拆卸线的实际应用能力。
1 斗链式混流拆卸线平衡问题
1.1 问题描述
斗链是一种生产组织方式,只需将工人按照作业效率从小到大的顺序分配到生产线上,生产线就能够实现自平衡,且达到最大生产效率。在斗链生产线中,工人按照各自效率朝着生产线下游方向作业,当遇到下游工人时即交接手中任务,同时沿生产线上游方向返回,直到遇到上游工人时即接替其手中任务,如此循环,工人最终将在固定的位置进行任务交接,工人作业区间固定,作业任务也固定,此时斗链系统收敛,生产线达到平衡,生产效率最高[2]。
在斗链拆卸线中,为实现生产线的平衡,不设固定工作站,工人可以按照各自作业效率来完成平衡状态时的任务量。在理想斗链系统中,作业速度远大于传送带速度和返回速度,故不考虑传送带速度和返回速度对系统的影响,但在拆卸线中工人作业速度并非远大于返回速度,故需要考虑返回速度对系统平衡性的影响。文献[20]已验证了考虑返回速度时斗链系统依然能够收敛,且每个工人的作业时间与返回时间之和相等。将斗链拆卸线上所有任务归一化为1,工人m与工人m+1之间的交接位置
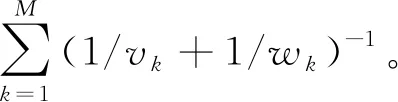
(1)
式中:vk表示工人k的作业速度,wk表示工人k的返回速度,M表示总工人数,且k,m=1, 2, …,M。
工人m的工作区间
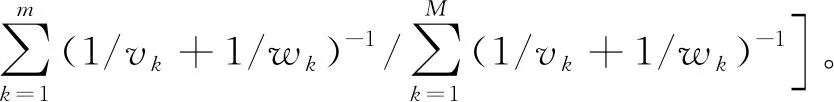
(2)
工人m的作业任务比重
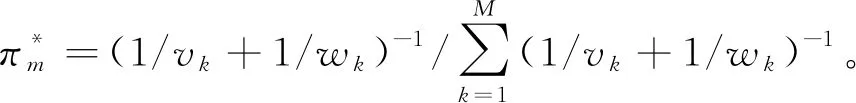
(3)
在斗链拆卸线中,将所有零部件的平均作业时间之和视为所有工人需要完成的总任务量,而每个工人将按照各自的作业效率完成平衡区间内的任务量。待拆卸产品一般多样化,为提高拆卸线的利用率,可将具有相似结构的同类产品放在同一拆卸线上进行拆卸作业,实现同类产品的混流拆卸。根据各品种中的零件优先关系建立综合优先关系图,不同品种的产品零件不尽相同,引入零件存在变量δnq,

(4)
则在混流拆卸线中零件n的综合拆卸时间

(5)
式中:ωq为品种q的拆卸比例,tnq为品种q中零件n的拆卸时间,Q为总的品种数,q=1, 2, …,Q。
斗链拆卸线中工人的作业速度不同,但在工作区间内完成各自拆卸任务所需的时间相同,可将该时间类比于传统拆卸线中的节拍。为确保完成拆卸任务量,拆卸线上的工人数及其作业速度需满足
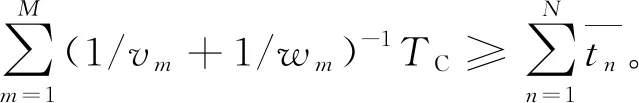
(6)
其中TC表示拆卸线节拍,即完成单位比例下的Q种产品时,每个拆卸工人的有效作业时间,其表达式为
(7)
式中:ηL表示生产线效率,因实际拆卸线上并非所有工作时间都为有效工作时间,生产线效率表示有效作业时间与工作时间之比,故0<ηL<1;R表示单位小时的拆卸任务量,
(8)
式中:Dy表示年拆卸量,Wy表示年工作周数,Sw表示每周的工作天数,Hs表示每天的工作时间(小时)。
在拆卸线中还需要考虑零部件的拆卸需求和危害性。零件n的拆卸需求量dn是根据其价值和市场需求量来确定的,其危害性hn为0-1变量,有
(9)
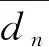
(10)

(11)
传统拆卸线中固定工作站和节拍时间,而斗链拆卸线突破节拍时间的限制,但在离散问题中,斗链系统难以保证每名工人的作业时间与理论作业区间完全吻合,工人实际作业时间可能小于、等于或大于理论作业时间,即存在等待或超越现象,这些都将影响生产线的效率。故在分配任务时尽量使实际作业时间与理论作业时间相等,即减小作业区间的不均衡性。待拆卸产品的中存在一些高价值、高需求的零部件,以及某些对环境或人体有危害的零部件,这些零部件均需尽早拆除,以提高拆卸收益并降低拆卸危害性。故拆卸线平衡问题是一项复杂的多目标优化问题。
1.2 数学模型
针对多目标斗链式混流拆卸线平衡特性建立其数学模型,以寻求可行拆卸序列,同时满足最小化作业区间负荷均衡性、尽早拆除高需求和有危害零部件的要求。
(1)除1.1节已解释的符号外,数学模型中还用到以下符号,其含义分别为:
M为斗链式拆卸线上作业工人数;
m为作业工人的编号,即作业区间编号,m∈{1, 2,…,M};
N为拆卸产品需要进行拆卸的任务数;
n为拆卸任务编号,n∈{1, 2,…,N};


xmn为拆卸任务与作业区间的关系;
ln为拆卸任务n在拆卸序列中的位置;
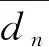

vm为第m个工人的作业速度;
wm为第m个工人的返回速度;
a,b为作业区间编号,a,b∈{1, 2,…,M};
i,j为拆卸任务编号,i,j∈{1, 2,…,N};
yij为任务i,j间优先关系值,可以构造拆卸任务间优先关系矩阵Y,其中Y=[yij]N×N。
(2)数学模型中的决策变量:
(3)数学模型中的辅助变量:
(4)目标函数和约束条件如下:

(12)

(13)
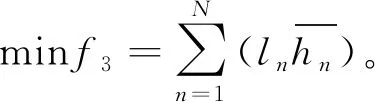
(14)

∀m∈{1,2,…,M};
(15)
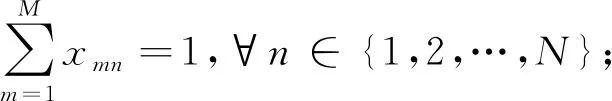
(16)

(17)
xmn∈{0,1},∀m∈{1,2,…,M},
n∈{1,2,…,N}。
(18)
目标函数中:式(12)表示最小化作业区间负荷均衡指标;式(13)表示最小化需求指标;式(14)表示最小化危害指标。约束条件中:式(15)表示第m个工人的理论作业时间;式(16)表示每一项任务都必须拆卸,且只能分配到一个作业区间进行拆卸;式(17)表示拆卸顺序必须满足任务间优先关系约束;式(18)表示任务分配变量是0-1型变量。
2 Pareto花朵授粉算法
花朵授粉算法(Flower Pollination Algorithm, FAP)是模拟花朵的自花与异花两种授粉特性而提出的,具有较好的全局搜索能力[21]。且该算法结构简单,所需设置的参数少,并已成功应用于拆卸序列规划等离散组合优化问题中。鉴于斗链式混流拆卸线平衡问题的复杂性和求解难度,设计适用于求解该问题的高效方法,主要包括花朵授粉算法中连续性操作的离散化,以及Pareto解集和多目标处理方法。
2.1 编码
编码是根据拆卸线平衡问题的特点构造可行拆卸序列,现有文献中多为随机编码方式,但受问题约束条件的限制,随机编码极易产生不可行解,这将对算法的效率产生不利影响,为此,本文采用基于优先关系矩阵挑选任务的方式进行编码,确保编码结果均为可行解。
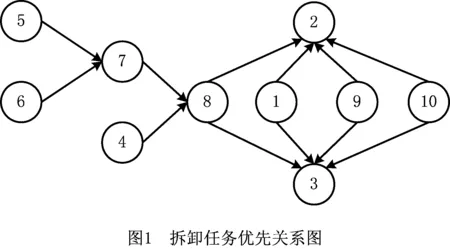
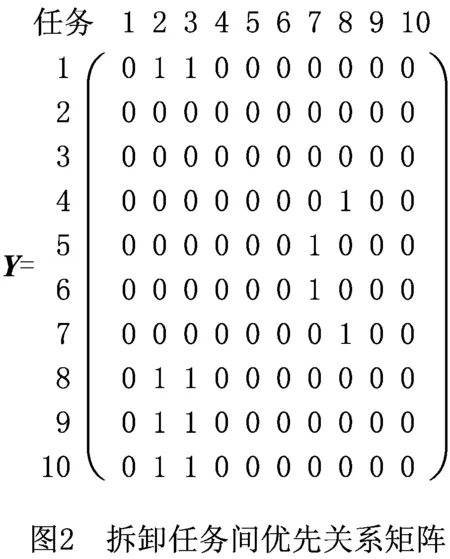
根据拆卸任务间的物理约束与几何约束建立拆卸任务间的优先关系图,如图1所示,圆圈内数字代表拆卸任务,箭头连接的两任务间存在拆卸顺序先后约束。根据优先关系图可以构建拆卸任务间的优先关系矩阵Y,其维度与拆卸任务相同,矩阵中的元素为0-1变量,用1.1节中的yij表示,图1中任务的优先关系矩阵如图2所示。
基于优先关系矩阵的编码需要逐个挑选任务,矩阵中所在列全为0的未分配任务即为候选任务。当存在多个候选任务时,为得到较优的初始序列,结合1.1节中的问题特征,建立如下3种启发式规则。
规则1优先挑选使得作业区间的实际作业时间与理论作业时间之差最小的任务,其数学表达式为
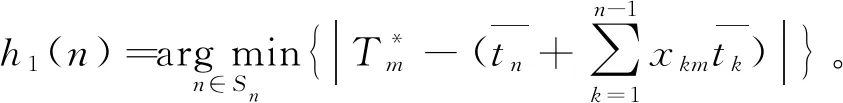
(19)

规则2优先挑选需求量最高的任务,从而使得需求指标f2最小,其表达式为

(20)
规则3优先挑选危害性最大的任务,从而使得危害性指标f3最小,其表达式为
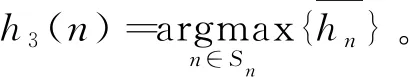
(21)
在编码过程中,候选任务很难同时满足3种启发式规则,而三种启发式规则又与3个目标函数相对应,优化过程中不设置各目标的优化顺序,若存在多个满足各启发式规则的任务,则随机挑选某一任务,从而确保了初始解的多样性。
2.2 解码
解码过程是将编码得到的拆卸序列中的任务分配到各个工作区间,并确定各个工作区间内任务的先后顺序。解码时遵循工作区间作业时间与理论作业时间之差最小化原则,其示意图如图3所示。图中:n表示任务编号,m表示工作区间编号,TR表示工作区间理论剩余时间,Sm表示已分配到工作区间m的任务集。

2.3 多目标处理方法
在多目标问题中是通过解之间的支配关系来确定解的优劣,对于任意的两个可行解X1、X2,若X1和X2满足式(22),则称X1Pareto占优于X2,或X1支配X2,记为X1X2。可行解X1与X2之间存在支配、被支配以及互不支配3种关系。

(22)
在多目标问题中,将所得的所有可行解进行支配关系比较,筛选出最终的互不支配解,即为Pareto非劣解。一般地,多目标的非劣解不止一个,而是由多个非劣解组成的Pareto非劣解集合,非劣解集对应的目标空间称为Pareto前沿。
将非劣解存储于外部档案中,算法在迭代过程中,需要将每次获得的新解与外部档案中的非劣解进行比较,添加支配解和互不支配解,删除被支配解,从而实现外部档案的更新。
借鉴带精英策略的快速非支配排序遗传算法(fast elitist Non-dominated Sorting Genetic Algorithm, NSGA-Ⅱ)拥挤距离机制[22]进行非劣解的评价筛选,先将每个子目标函数值按升序进行排列,然后计算子拥挤距离,每个非劣解的拥挤距离为所有子拥挤距离之和,其表达式为

(23)
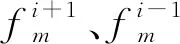
2.4 Pareto解集评价
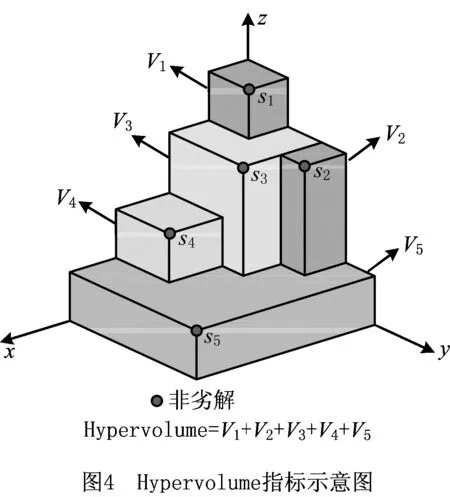
支配关系反映的是非劣解之间的优劣关系,无法对Pareto解集进行评价,为此,本文引入Hypervolume指标[23]对算法迭代过程中求得的Pareto解集进行评价。Hypervolume指标所求得的所有非劣解到参考解之间的超体积。在算法迭代过程中,随着非劣解不断逼近真实Pareto前沿,Hypervolume值将不断增大,当算法收敛时,即所有非劣解达到真实Pareto前沿时,Hypervolume值最大。
如图4所示,在求最大值的3个目标的目标空间中,非劣解集为{S1,S2,S3,S4,S5},参考点为原点O,各非劣解到O的有效超体积分别为V1,V2,V3,V4,V5,则Hypervolume=V1+V2+V3+V4+V5。Hypervolume值不仅可以反映算法迭代过程中解的质量变化情况,还可以用于比较不同算法所得非劣解的性能。
2.5 离散花朵授粉算法
花朵授粉算法包括异花授粉和自花授粉两种操作。异花授粉主要通过鸟类和昆虫等具有莱维飞行特征的生物进行传粉,表现为全局搜索方式;自花授粉方式是花粉在自身花朵上进行传播,表现为局部寻优方式。通过概率Ps来决定采用全局授粉方式或局部授粉方式。
在花朵授粉算法中,设花朵种群规模为Npop,算法最大迭代次数为gmax,对任一的花朵i(i=1, 2,…,Npop)在第g(g=1, 2,…,gmax)次迭代时,异花授粉表达式为
(24)

(25)
式中:λ为常数,且λ=1.5,Γ(λ)是Gamma函数,s由式(26)得到:
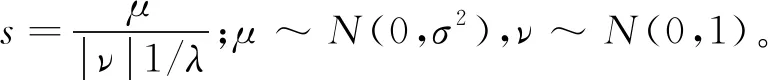
(26)
式中:
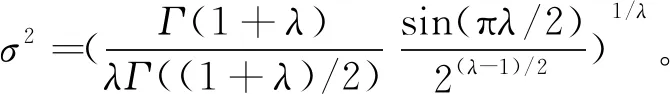
(27)
自花授粉表达式为

(28)
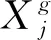
在拆卸线平衡问题中,将每一花朵定义为一个可行拆卸序列,因拆卸线平衡问题是离散问题,上式中的连续性花朵授粉方式不再适用,且授粉后的花朵需要满足拆卸优先关系,为此需要设计满足问题要求的离散花朵授粉行为。参考离散粒子群算法的操作方式,对异花授粉和自花授粉方式进行离散化,离散后的两授粉表达式分别为
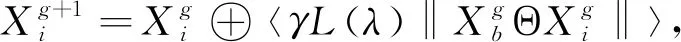
(29)
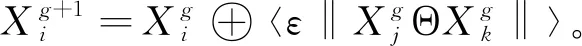
(30)
式中:Θ表示两序列中对应位置处的任务不同时的交换操作,其中一个任务通过执行交换操作,趋近于另外一个任务,且交换任务时需要满足优先关系约束,若序列中对应位置处的任务相同,则无需执行交换操作;‖·‖表示每个相异任务可执行交换的次数;A⊕〈B〉表示对序列A执行B中的交换对。
离散过程中,γL(λ)以及ε与交换总次数的乘积向上取整,当L(λ)<0时不执行交换操作。交换操作时,如序列X1与X2中第n处任务不同,X2中第n处的任务i的最近紧前任务和最近紧后任务之间的任务集合为S1,且S1中任务j的最近紧前任务和最近紧后任务之间的任务集合为S2,若S1∩S2≠∅,则X2中任务i和任务j可以交换,i和j为一对可行交换对,‖X1ΘX2‖即为序列X1与X2之间的所有可行交换对数,交换对数乘以系数γ做向上取整处理,即〈γ‖X1ΘX2‖〉=γ‖X1ΘX2‖⎤。
2.6 算法流程
将离散花朵授粉算法与多目标优化方法相结合,构造Pareto花朵授粉算法,用于求解多目标斗链式混流拆卸线平衡问题。所提算法的具体流程如下:
步骤1参数初始化,设置种群规模Npop,算法迭代次数gmax,花朵授粉方式转换概率PS,外部档案Q=∅。
步骤2种群初始化,随机生成初始可行花朵,并计算每个花朵的适应度值F=[f1,f2,f3]。
步骤3根据Pareto支配关系筛选非劣解,并将非劣解集存储于外部档案Q中。

步骤5循环迭代开始,令当前迭代次数g=1。
步骤6对每个花朵执行授粉行为,令当前花朵编号i=1。


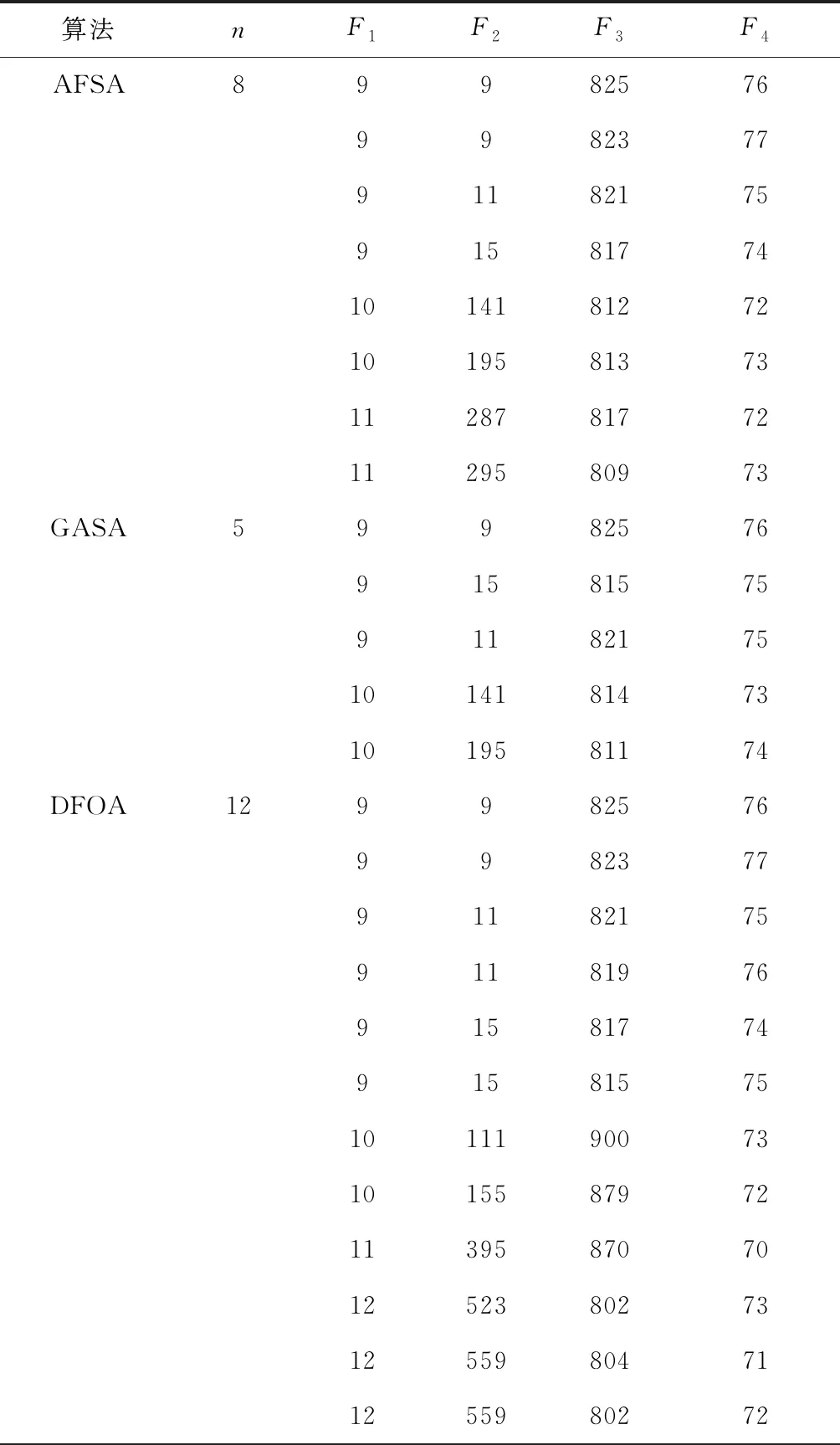
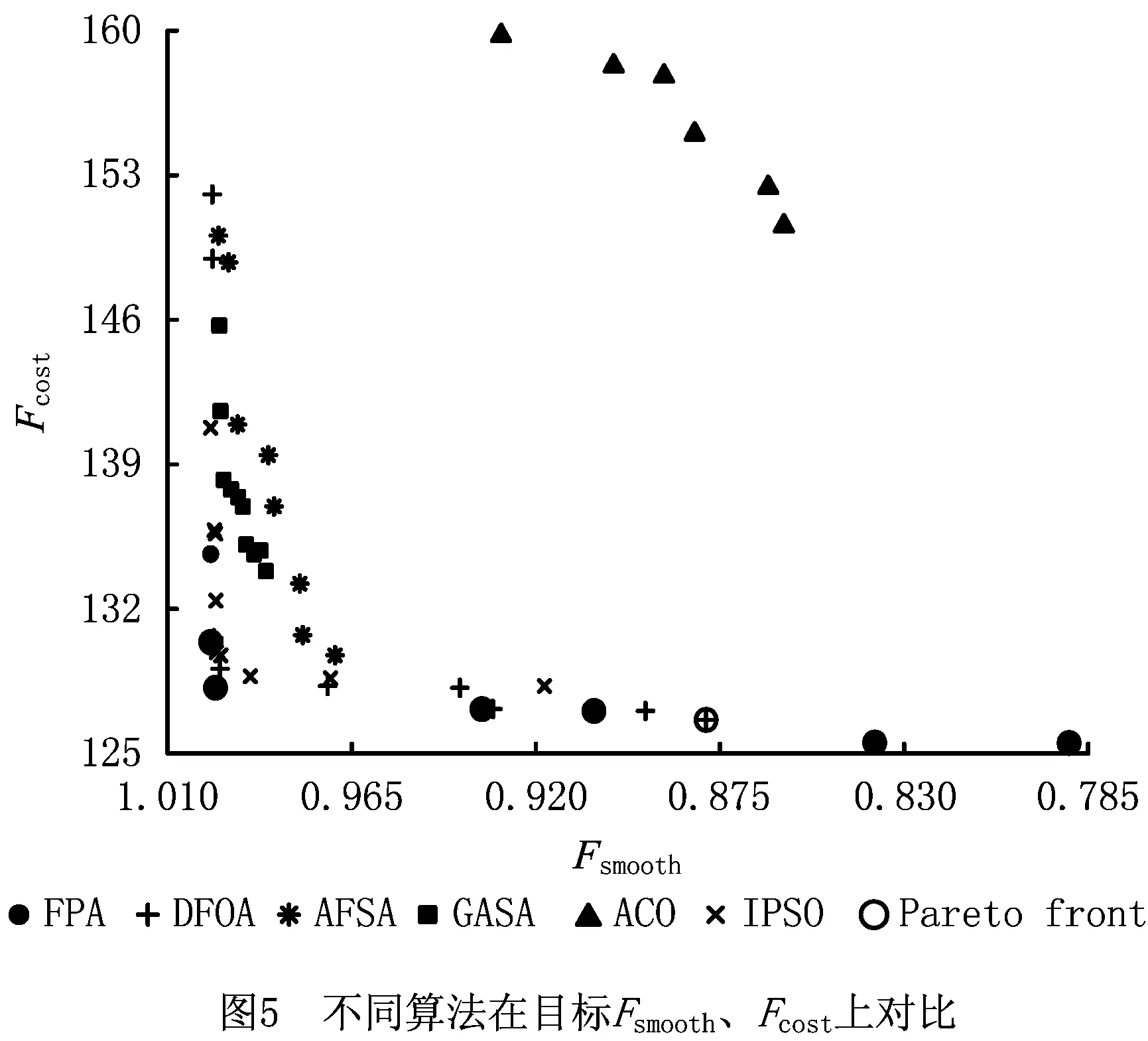
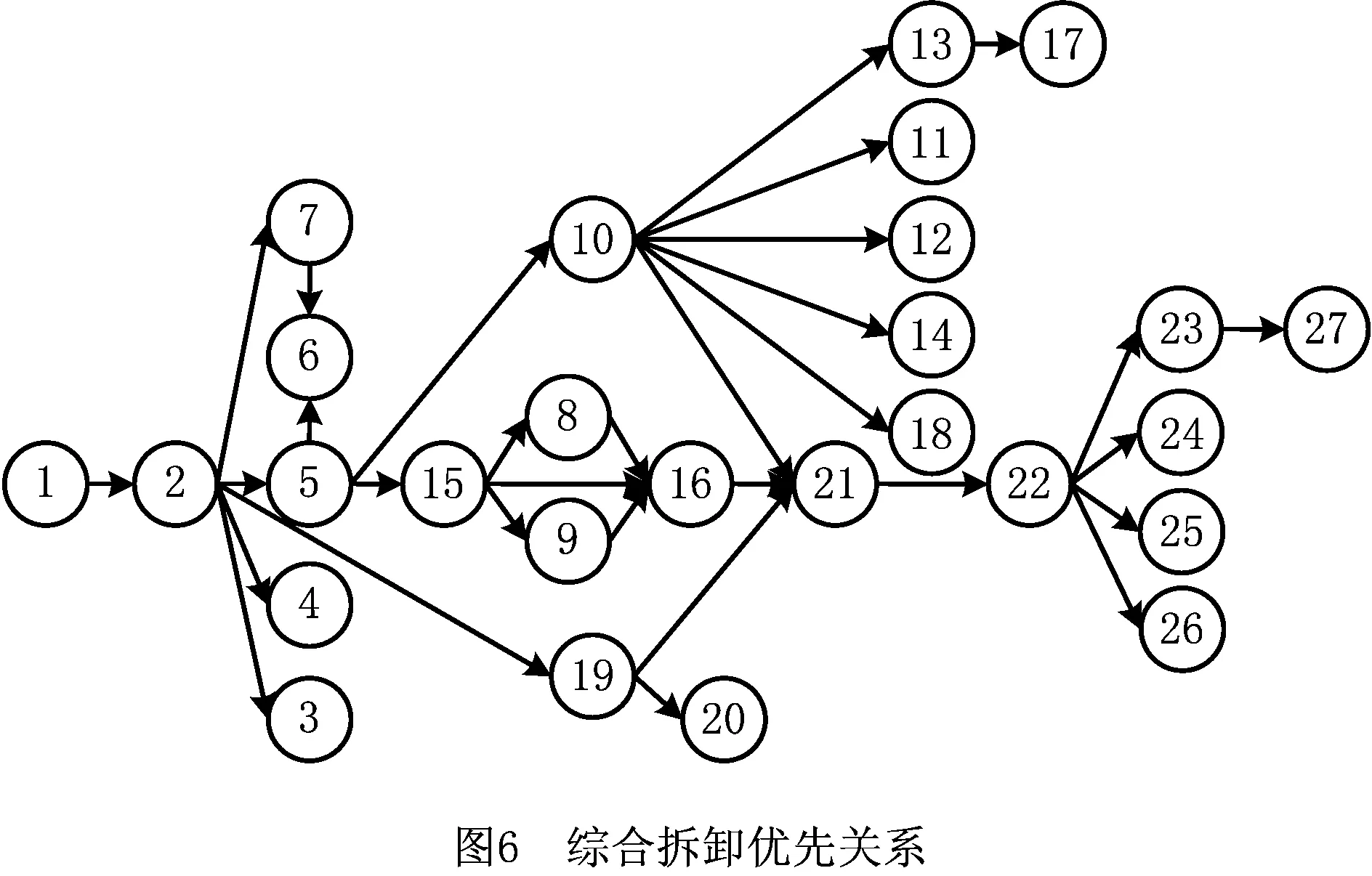
步骤10若i 步骤11根据Pareto支配关系更新外部档案Q。 步骤12更新种群,将外部档案中非劣解作为种群。计算外部档案中非劣解个数NQ,若NQ>Npop,则挑选拥挤距离较大的Npop个非劣解作为种群,否则随机生成新的花朵添加到种群中以维持种群规模。 步骤13若g 步骤14寻优结束,输出外部档案中的Pareto解集及其适应度函数。 为验证所提算法的有效性,针对不同规模的拆卸线平衡问题进行测试。算法实验采用的计算机硬件配置为Inter Core i3-2100 M, 3.10 GHz, 2 GB内存,在Windows 7系统下采用MATLAB R2017b软件开发了算法的实验程序。现有文献中尚未发现有关斗链式混流拆卸线实例报道,故只能采用其他类型的拆卸线实例进行算法验证。针对不同类型的拆卸线算例,拆卸线平衡问题的本质特征并未改变,只需根据问题特征改变算法的编码和解码操作,而离散花朵授粉算法的授粉行为方式不变,故可以采用其他类型的拆卸线实例对所提算法的求解性能进行验证。 现有文献中求解完全拆卸线算例主要包括25项拆卸任务的某型号手机拆卸线(P25)和含52项拆卸任务的电子套结机机壳拆卸线(P52)。P25的目标函数包括最小化工作站数F1、负荷均衡指标F2、需求指标F3和危害指标F4;P52的目标函数包括闲置率Fidle、平滑率Fsmooth和拆卸成本Fcost。采用本文所提Pareto离散花朵授粉算法对两算例进行求解,并与现有文献中的算法结果进行对比。 现有文献中求解P25的多目标算法包括人工鱼群算法(Artificial Fish Swarm Algorithm, AFSA)[16]、遗传模拟退火(Genetic Algorithm and Simulated Annealing, GASA)算法[17]、离散果蝇优化算法(Discrete Fruit Fly Optimization Algorithm, DFOA)[18]、萤火虫算法(Firefly Algorithm, FA)[19]、离散布谷鸟搜索(Discrete Cuckoo Search, DCS)算法[24]、蝙蝠算法(Bat Algorithm, BA)[25]。多目标算法的求解结果如表1所示,表中n表示算法所得非劣解的个数。本文FPA的参数设置为:Npop=50,gmax=200,PS=0.8。因问题规模较小,保留求解过程中外部档案中的所有非劣解,共求解30次,平均求解时间为18.97 s。在30次求解结果中共有25次均求得36个相同非劣解,且该非劣解集为30次求解结果中的最好解,所有非劣解的目标函数值如表1所示,具体平衡方案见附录中表1。 表1 现有文献多目标求解P25结果 续表1 续表1 由表1可知, AFSA、GASA、DFOA、FA、DCS、BA、FPA等多目标算法能够求得多个非劣解,每个平衡方案各有侧重点,从而验证了多目标算法的有效性。分析表1中数据可知,AFSA、GASA、DFOA、FA、DCS、BA求得非劣解的数目有限,而FPA一次能够求得36个非劣解,且FPA的非劣解集中包含了其他多目标算法的最好非劣解,FPA的非劣解更接近问题的真实Pareto前沿,表明FPA的寻优能力更强。FPA求解P25的结果为现有文献中已知的最好非劣解集,因该问题的真实Pareto前沿未知,在针对该问题的后续研究中,可将其作为其他方法求解性能的参考值。 在求解P52时,现有文献中的求解方法包括粒子群优化(Particle Swarm Optimization, PSO)[14]、AFSA[16]、GASA[17]、DFOA[18]、改进粒子群优化(Improved PSO, IPSO)算法[26]。采用本文所提FPA对P52进行求解,参数设置为:Npop=50,gmax=200,PS=0.8。算法共运行20次,平均运行时间为142.81 s,取20次结果中的较优解,共求得8个非劣解,具体平衡方案及其目标函数值见附录中表2。所有非劣解在目标空间中的分布与其他5种多目标算法结果对比,如图5所示。除了ACO中4个非劣解的Fidle=0.175 7外,其他所有算法的非劣解的Fidle=0.057 9,故只选取ACO中Fidle=0.057 9的较优解进行对比。为便于对比各非劣解的优劣,图5给出了所有非劣解在目标Fsmooth与Fcost上的对比情况,并对所有非劣解再次进行Pareto筛选,所得Pareto前沿已在图5中进行了标示。新的Pareto前沿共包含8个非劣解,其中7个非劣解来自FPA,另外一个非劣解来自DFOA,由此可知FPA的求解性能优于其他7种多目标算法。 在单目标极值探索方面,FPA的非劣解在目标Fsmooth与Fcost上均有所提高,Fsmooth最优值为0.999 5,Fcost的最优值为125.502,均为现有文献中的已知最好结果。综上分析可知,在求解完全拆卸的小规模问题(P25)和大规模问题(P52)中,本文所提FPA均表现出较优的求解性能。 3.1节中的两个算例均为完全拆卸线平衡问题,现有研究中已将拆卸线平衡问题拓展到了部分拆卸线平衡问题,因部分拆卸线平衡问题的可行域更大,故其求解更加复杂。文献[24,26]分别采用IPSO和DCS对含55项拆卸任务的不完全拆卸线算例(P55)进行求解,分别得到3个和9个平衡方案。该算例包括4个目标函数,分别为拆卸任务数F1、工作站数F2、空闲均衡指标F3、拆卸成本F4,TC为实际节拍。采用本文所提FPA对该算例进行求解,设Npop=50,gmax=200,PS=0.8,共求得5个平衡方案,如表2所示。 表2 FPA求解P55结果 将FPA与IPSO、DCS计算所得的非劣解分别在4个目标及TC上进行对比,分别对比最小值(min)、均值(avg)和最大值(max),如表3所示。由表3对比可知,FPA方案在4个目标和TC上的最小值、平均值、最大值均优于IPSO与DCS的方案。FPA取得最小拆卸任务数34;工作站数和DCS相同,均为3个工作站;空闲负荷均衡指标最小值都为0,但FPA的均值要小于DCS的均值;拆卸成本方面,FPA能达到最小拆卸成本3.519,其均值比IPSO与DCS分别提高了33.74%和7.84%;节拍也相应减小,FPA最小节拍为135,比IPSO、DCS最小节拍分别减小10和7,从而验证了FPA比IPSO、DCS更具优越性。 表3 FPA与IPSO、DCS求解P55结果对比 课题组在某拆卸企业现场调研,得到废旧电视机相关拆卸案例数据。待拆卸的电视机有3种不同品种,共含27个零部件,各品种电视机的年拆卸量分别为Q1=30 000,Q2=40 000,Q3=30 000,则最小拆卸品种比例为ω1∶ω2∶ω3=3∶4∶3,具体拆卸信息如表4所示,根据各品种零部件间优先关系绘制如图6所示的综合拆卸优先关系图。建立3种品种的电视机混流拆卸线,采用斗链生产组织方式,该生产线上的相关参数分别为Wy=42,Sw=5,Hs=8,ηL=0.9。设该拆卸线上工人数为3人,作业速度分别为v1=1.1,v2=1.2,v3=1.3,返回速度分别为w1=11,w2=12,w3=13,经计算工人数及其作业速度满足生产要求。 表4 电视机零部件信息 续表4 采用Pareto花朵授粉算法对实例进行求解,兼顾求解质量与求解效率,将算法参数设定为:Npop=50,gmax=100,PS=0.8,计算Hypervolume值的参考点设为(50, 2 000, 100)。算法共运行10次,平均运算时间为114.28 s,取其中一次较优结果,其Hypervolume值随迭代次数的变化如图7所示,共求得90个非劣解,非劣解的Pareto前沿如图8所示。 表5 拆卸平衡方案 在3种方案中:方案S1取得目标f1上的最小值0,且所有f1= 0的方案在目标f2上相差不大,而S1的目标f3最小,此时f3= 60;方案S2在所有方案中的目标f2上取得最小值1 186.8,若要求需求指标最小,可以选择方案S2;方案S3的目标f3为最小值46,取得f3= 46的方案共有4个,而方案S2能同时兼顾目标f1和f2,使得两目标不至于过大,故方案S3为要求危害指标最小的折中方案。决策者除了考虑单目标要求外,也可以同时兼顾两个目标进行方案选择,目标侧重点不同,方案选择也不同,所得90种平衡方案丰富了决策者的决策空间,为斗链式混流拆卸线的作业任务安排提供了参考。 针对传统拆卸线难以实现作业均衡这一难题,将具有自平衡性的斗链生产组织方式应用于拆卸线中,并结合待拆卸产品的多样性与结构相似性,建立斗链生产组织方式下的多目标混流拆卸线平衡问题数学模型,进而设计了Pareto离散花朵授粉算法用于求解该问题。在所设计算法中,采用结合问题特征的启发式方法来构造初始可行解,并提出了多目标优化策略。将花朵授粉算法离散化,设计了基于莱维飞行的离散异花授粉操作和随机离散自花授粉操作,增强了算法的全局搜索能力和局部搜索能力,同时确保了操作结果的可行性。 在求解25项拆卸任务算例中,所提算法得到现有研究中已知最优的36个非劣解;在求解52项拆卸任务算例中,所得结果进一步逼近真实Pareto前沿;将所提算法的验证拓展到部分拆卸线平衡问题中,其性能优于已知多目标改进粒子群算法和多目标布谷鸟算法。并将所设计模型和所提算法应求解混合品种电视机拆卸线平衡问题中,得到90个非劣解,验证了斗链生产组织方式下拆卸线的平衡,为决策者提供了多种可选平衡方案。 后续研究可以考虑将斗链生产组织方式应用于其他复杂生产线中,积极探索更加高效策略来提升方法的求解性能,扩大斗链理论研究的实际应用价值。3 算法验证
3.1 完全拆卸线算例

3.2 部分拆卸线算例


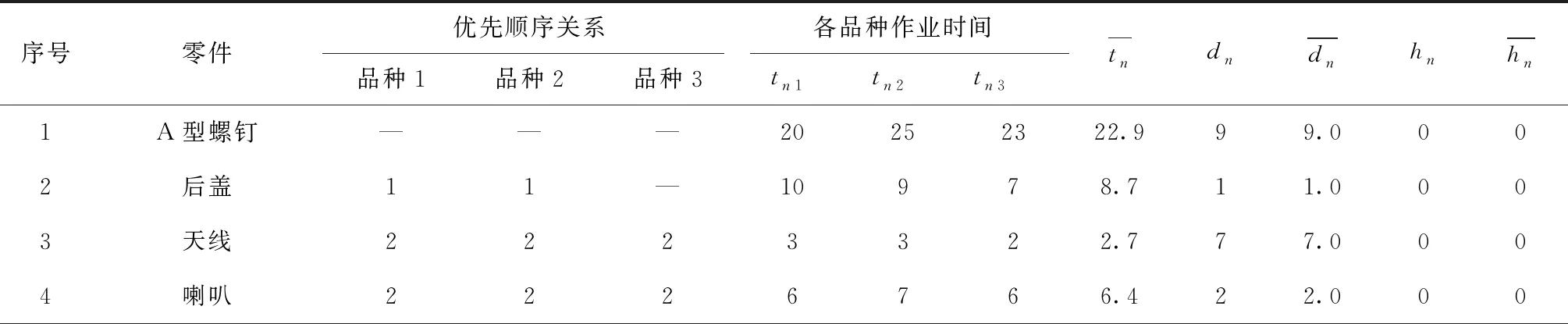
4 实例应用





5 结束语
