考虑运输的柔性流水车间多处理器任务调度的混合遗传优化算法

轩 华，王 潞，李 冰，王薛苑

(郑州大学 管理工程学院，河南 郑州 450001)

0 引言

柔性流水车间(Flexible Flow-Shop, FFS)结构在很多工业环境都较为常见，例如半导体制造、钢铁、电子制造、制药等行业[1]。基于其复杂性和实用性，FFS问题无论在理论还是实践领域都有着较强的研究价值。但由于实际生产中存在一个工件由多台机器同时处理的情况，如船舶选址、诊断微处理器系统、半导体制造等[2-3]，本文提出带运输时间和释放时间的FFS多处理器任务调度问题(Multiprocessor Task Scheduling Problem in Flexible Flowshops，MTSP-FFS)。因为MTSP-FFS是强NP-hard[3-4]问题，所以Fk(Pm1,…,Pmk)|sizeik,tk,k+1,ri|Cmax也是强NP-hard问题。

针对MTSP，文献[5]综合两种不同的人工蚁群提出了一个混合方法以最小化流程完成时间。文献[6]证明了利用传统的最早开始时间方法解决分配问题并不合适，基于蚁群优化算法引入了一种新方法以最小化最大完工时间。文献[7]考虑了优先级和截止时间约束，提出了混合随机进化算法的遗传算法，目标是最小化耗电量。文献[8]提出了离散粒子群算法分别最小化最大完工时间，流程时间和可靠度成本。文献[9]提出一个分配和开始时间计算算法来解决多处理器非抢占严格周期性实时任务调度问题。文献[10]则针对带多处理器任务的作业车间调度问题，设计了混合粒子群优化算法以最小化最大完工时间。

针对多阶段MTSP-FFS，为最小化最大完工时间，文献[11]利用结构启发式求解了两阶段问题。针对多阶段最大完工时间问题，文献[12]提出了并行贪婪算法，它通过破坏和重建两个阶段进行迭代；文献[13]改进了遗传算法的变异算子，基于最优调度值提出了一种有效的遗传算法；文献[1]设计了结合双向计划的人工蜂群算法；文献[14]提出了一些新的分派规则和一个免疫算法；文献[15]基于人工免疫系统和迭代贪婪算法的特点提出了新的混合免疫算法。为最小化总加权完成时间，文献[16]考虑工件动态到达、机器故障和运输时间等实际生产特征，分别结合次梯度法和交替S&B算法设计了拉格朗日松弛算法，解决了多阶段问题。

遗传算法(Genetic Algorithm, GA)在车间调度问题中的应用已较为普遍。为解决最大完工时间问题，文献[17]针对流水车间序列相关群调度，利用随机抽样搜索法和矩阵解码方案来改进GA；文献[18-19]分别提出了混合遗传—免疫算法和引入CDS(Campbell-Dudek-Simth)启发式的混合遗传算法求解置换流水车间调度；文献[20]将GA和禁忌搜索相结合提出了一种混合改进算法求解带集装工序的FFS有限能力物料需求计划系统；文献[21]针对柔性单件车间调度，引入启发式规则、基于混沌序列的邻域搜索提出了混合遗传算法。

从上述研究可看出，已有的求解MTSP-FFS的方法主要为智能优化算法，而对于解决该问题的GA的改进主要从算子和参数的设计两方面展开，且已有研究所解决的问题缺少对实际生产特征(如运输时间、工件动态到达)的考虑，因此，本文针对考虑运输时间的动态MTSP-FFS，提出一种结合迭代贪婪算法(Iterative Greedy Procedure, IGP)的混合GA(简称GA&IGP)以改善由GA得到的可行解，进而避免传统GA过早收敛陷入局部最优的问题。

1 问题建模

1.1 问题描述

本文研究的带运输时间的动态MTSP-FFS可描述为：有M个工件沿着同一个方向依次经过J个加工阶段进行加工，每个阶段s有Ns台并行机(Ns≥1)，至少有一个阶段有两台或两台以上的并行机，每个工件i至少会在一个加工阶段同时需要多台处理器进行加工。考虑到机器调度和运输计划间的协调问题，将运输时间与实际加工时间分开考虑，假定机器在整个加工时间段内总是持续可用的，而且加工工件过程中只指定机器数量，不指定具体机器，即工件i(i=1,…,M)在任一加工阶段s(s=1,…,J)加工时，可在任意sizeis台空闲机器进行处理。本文旨在考虑运输时间、工件动态到达等约束下，获取最小化最大完工时间的最佳调度时间表。

1.2 约束条件

(1)当工件需要多台处理器同时进行加工时，这些机器要持续被占用，直至该阶段工件完成加工。

(1)

式中：sizeis表示工件i在第s个加工阶段使用的机器数；δish为二元变量，当工件i在阶段s的机器h上加工时δish=1，否则δish=0。

(2)一道工序完成在机器上的加工后才能释放机器

Stis+Pis-1=Ftis。

(2)

式中：Stis表示工件i在第s个加工阶段时的开始时间(为该时刻的始端)；Ftis表示工件i在第s个加工阶段的完工时间(为该时刻的末端)；Pis表示工件i在第s个加工阶段的加工时间。

(3)加工每个工件时，只有完成前一个阶段的加工且运送至下一阶段，才能开始工件在下一阶段的加工。

Ftis+ts,s+1+1≤Sti,s+1。

(3)

式中ts,s+1表示工件从阶段s到阶段s+1的运输时间。

上述约束式(2)和约束式(3)中的“-1”和“+1”是由于定义的开始时间和完工时间在时刻的不同端点，因其时间的离散性而引起。

1.3 目标函数

目标为最小化最大完工时间：

(4)

本文研究的车间调度是在满足上述约束式(1)～约束式(3)的条件下最小化最大完工时间。

2 多阶段多处理器任务加工系统编码方案

MTSP-FFS调度模型不仅要考虑工件的加工顺序，还需为每个工件分配加工需要的机器。传统的编码方式难以解决该问题，本文基于多机并行加工的特点设计了基于多阶段多处理器任务加工系统(Multi-stage Multiprocessor Task System, MMTS)的编码方案。

2.1 工件加工机器流生成机制

(1)基于同构并行机组的多阶段加工系统

基于同构并行机组的多阶段加工系统有多个加工阶段，每个阶段由多台同构并行机组成，利用自然数编码形式对每台机器进行编号。如图1所示，msx为机器标号，表示位于第s个加工阶段的机器x(x=1,…,Ns)。

(2)基于MMTS的加工机器流表述

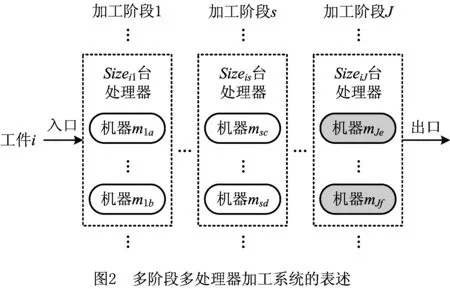
工件i依次在各加工阶段的同构并行机组内选择可利用的sizeis台空闲机器进行加工，从而形成工件加工机器流，如图2所示。

(3)基于机器空闲原则的加工流生成机制

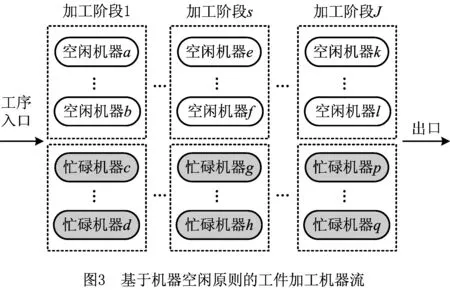
基于首要空闲机器原则，同构并行机组内有空闲机器才能被选择的原则，依次筛选各加工阶段内的机器。如果没有空闲同构并行机，则工件依次进行等待，待有空闲机器时再进行选择。具体流动机制如图3所示。

2.2 单工件加工机器流的编码

使用基于并行机机器号的工件加工机器流表述方法对多阶段多处理器任务加工系统进行编码表述。

(1)第一阶段

采取基于并行机机器号的工件加工机器流生成机制对工件在第一阶段的加工过程进行编码，作为元胞数组的第1列列向量。

(2)第s阶段

采取基于并行机机器号的工件加工机器流生成机制对工件在第s阶段的加工过程进行编码，分别作为元胞数组的第2列～第J列向量。

利用基于并行机机器号的工件加工机器流生成机制产生工件的多阶段加工机器流，从而形成元胞数组形式，如图4所示。

2.3 批量工件加工机器流的编码

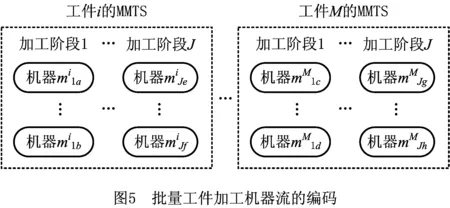
批量工件在MMTS中的加工流程采用上述的元胞数组编码方案，将多个工件的MMTS组合在一起就形成了由多个MMTS矩阵组成的元胞数组，如图5所示。

3 GA&IGP融合优化策略

多阶段MTSP-FFS属于NP-hard问题，利用传统算法难以解决。本文利用GA对MTSP-FFS问题进行求解，GA求解速度快但也存在很多问题，如它在求解过程中会随着问题规模的增大容易陷入局部最优。因此本文引入IGP克服GA的缺陷，同时针对不良后代进行改进，提高子代的适应度值。

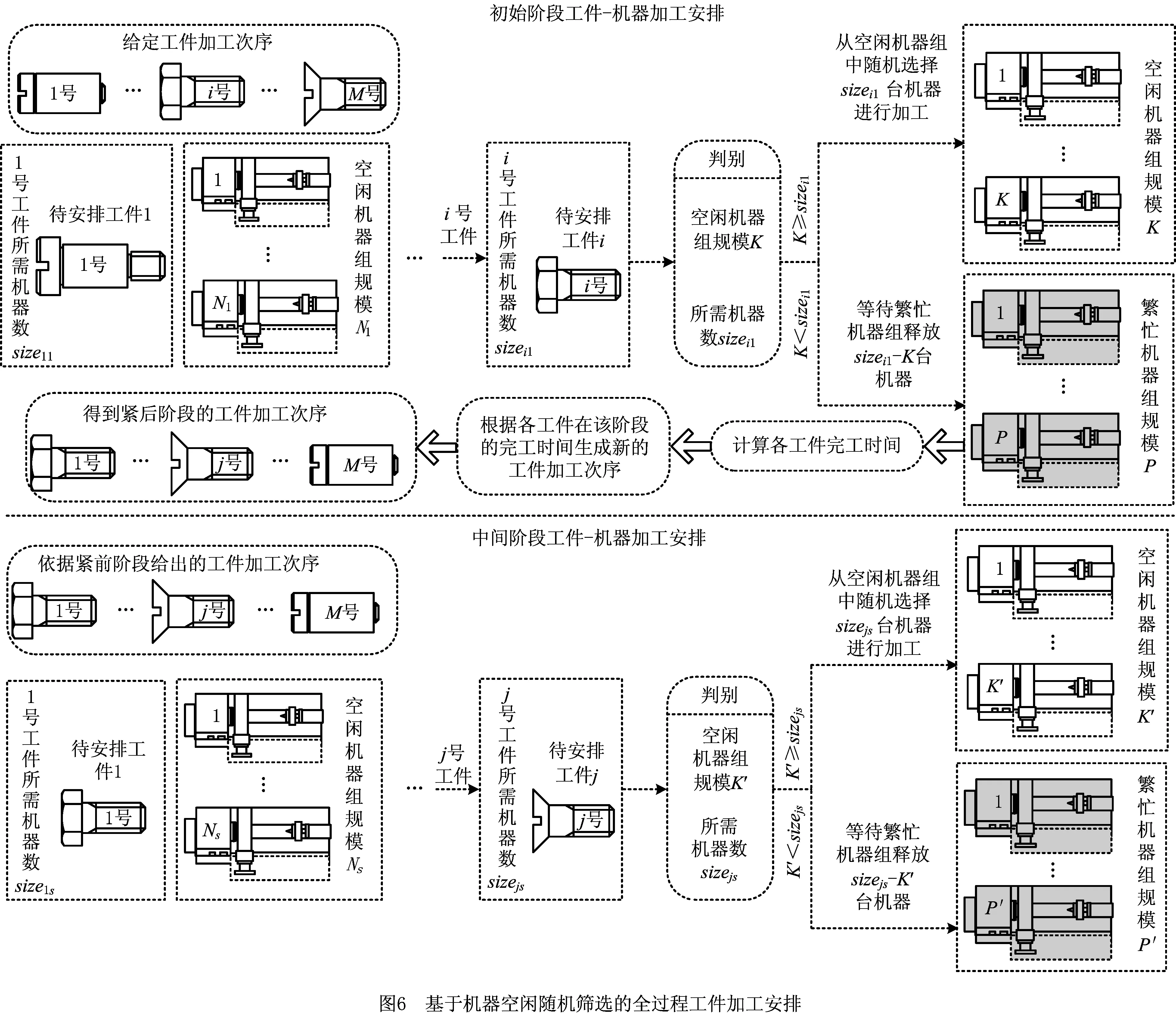
3.1 基于机器空闲随机筛选的工件安排机制

工件和机器安排中，利用首要空闲机器原则同时结合编码方案确定机器和工件的对应关系。首要空闲机器原则是指，当安排工件在阶段s进行加工且有多台可选择的机器时，以机器空闲作为选择的第一标准，而不考虑机器的释放时间，该过程称为基于机器空闲随机筛选的工件安排机制(Job Allocation Procedure with Randomly Selecting From Idle Machines, JAP-RSIM)。JAP-RSIM的工件—机器安排机制步骤如下：

步骤1初始阶段的工件—机器加工安排。

工件在第一阶段进行加工时，加工顺序按照给定的顺序进行安排。

(1)首先安排第一个工件进行加工，此时机器都处于空闲状态，不需要判断可以直接进行选择。

(2)在安排第i(i>1)个工件加工时，如果空闲机器数k小于sizei1,不满足该工件的加工要求，则该工件需要等待，直到空闲机器满足加工要求后再开始加工，接着安排下一个工件进行加工，直到该阶段的空闲机器数在该时间段无法满足任一工件的加工要求。考虑各工件在第一阶段的动态到达时间，根据各工件在第一阶段需要的机器数和加工时间，依次安排机器进行加工，直到所有工件在第一阶段完成加工。

步骤2其他阶段的工件—机器加工后安排。

当工件在s(s>1)阶段加工时，加工顺序依照工件在上一个阶段的完工时间来生成，即基于工件在第s-1个阶段完工时间的升序排列，形成第s阶段工件加工的顺序。工件加工安排和步骤1相同。

步骤3获取全过程的工件—机器加工安排。

当所有工件经过所有阶段完成加工后，记录工件在每个阶段的完工时间，选择最大的完工时间点就是整批工件的完成时间，即可行解的Makespan。

基于JAP-RSIM的全过程机器—工件加工安排如图6所示。

3.2 基于机器空闲随机筛选的初始解生成

对于组批工件中的各工件利用随机排序原则产生初始加工顺序，再结合JAP-RSIM过程基于空闲机器筛选原则安排各个工件对应的机器，进而产生初始可行解。在元胞数组中工件所处的位置就是该工件的加工顺序，工件采用直接编码的方式表示。

步骤1基于随机原则确定工件顺序。

步骤2基于JAP-RSIM过程确定机器排序。

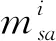
3.3 基于最小化最大完工时间的新解筛选机制

由于MTSP-FFS模型的目标值定义为最小化最大完工时间，因此将工件完工时间的倒数定义为个体的适应度值，即f(y)=1/Ftmax(y)，其中y代表了组批工件的一个完整工件排序。选择过程采取精英策略的思想，让优秀的工件顺序更容易进入迭代环节。

步骤1计算选择概率，每个个体y的选择概率由自身的适应度值所决定(n为个体总数)：

选择时随机产生一个r，由随机数r确定选择的区间范围。

步骤2根据计算的适应度值，引入轮盘赌规则，总完工时间越小的调度方案被选中的概率越高。

3.4 GA&IGP的新解更新过程

传统GA随着求解问题规模的扩大，往往会过早收敛陷入局部最优，因此，设计GA&IGP混合更新过程，利用IGP改进由GA获取的可行解，进而提高GA的效率。

步骤1交叉与变异概率的初始化设置。

交叉和变异是GA算法中重要的算子，会直接影响遗传算法的效率和结果的有效性，概率过大会遗失优秀个体的信息，概率过小又会使得改进效率较低收敛过慢。通过测试不同的参数以及根据文献[13]的全因子实验设计结果，选定交叉概率为0.5，变异概率为0.01的参数组合。

步骤2基于工件顺序与加工机器流同步交叉的新解更新过程。

(1)工件加工顺序组选择。

基于交叉概率随机从现有的加工工件顺序组合中选择两个排序组，记为sequence(u)={u1,…,uM}和sequence(v)={v1,…,vM}，其中{u1,…,uM}和{v1,…,vM}均为工件号。

(2)生成工件加工顺序组MMTS。

针对两个工件加工顺序组sequence(u)和sequence(v)，分别利用MMTS表述工件加工顺序组中各工件的加工机器流，从而形成工件加工顺序组的MMTS系统，记为：

MMTS{sequence(u)}={MMTS(u1),…,

MMTS(uM)}，

MMTS{sequence(v)}={MMTS(v1),…,

MMTS(vM)}。

(3)基于工件加工顺序组MMTS的随机位单点倒置交叉。

为使工件顺序与加工机器流同步进行更新，采用单工件交叉规则，从工件顺序组sequence(u)中随机选择工件A，从工件顺序组sequence(v)中随机选择工件A′。将sequence(u)中工件A及其之前工件的加工机器流，记为MMTS{sequence(u|A)}；将sequence(u)工件A之后的工件的加工机器流，记为MMTS{sequence(u|B)}；将sequence(v)中工件A′及其之前工件的加工机器流，记为MMTS{sequence(v|A′)}；将sequence(v)中工件A′之后的工件的加工机器流，记为MMTS{sequence(v|B′)}。即

MMTS{sequence(u|A)}=

{MMTS(u1),…,MMTS(A)}，

MMTS{sequence(v|A′)}=

{MMTS(v1),…,MMTS(A′))}，

MMTS{sequence(u|B)}=

{MMTS(B),…,MMTS(uM)}，

MMTS{sequence(v|B′)}=

{MMTS(B),…,MMTS(vM)}。

将工件顺序组sequence(u|A)与sequence(v|A′)进行翻转交叉得到新的工件排序记为sequence(u′)和sequence(v′)。

基于工件加工顺序组MMTS随机位单点倒置交叉的新解更新过程如图7所示。

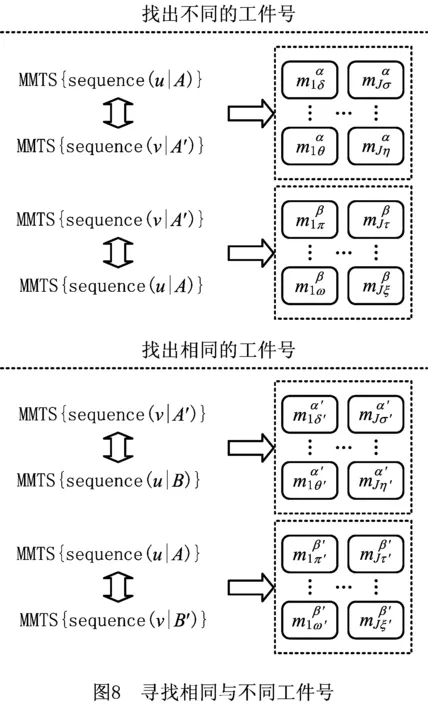
(4)找出不同工件号的MMTS。

将sequence(A)与sequence(A′)进行对比，找出sequence(A)中不同的工件号并保存，记为α；找出sequence(A′)中不同的工件号并保存，记为β。

(5)剔除相同工件号的MMTS。

单点交叉后，分别检测sequence(u′)和sequence(v′)是否有同一工件号出现两次的情况，即比较sequence(A′)和sequence(B)的工件加工顺序，找出相同的工件号，记为α′；比较sequence(A)和sequence(B′)的工件加工顺序，找出相同的工件号，记为β′，将重复出现的工件号从MMTS去除并保留该位置。

(6)修正工件加工顺序组。

利用保存的工件号依次替代(5)中删除的工件号，直到sequence(u′)和sequence(v′)中不出现重复的工件。

具体操作如图8所示。

步骤3基于工件顺序与加工机器流同步变异的新解调整过程。

(1)根据变异概率从解群中选取一个完整的组批工件加工顺序，即sequence(p)，利用MMTS表述工件加工顺序组中各工件的加工机器流，从而形成工件加工顺序组的MMTS系统，即

MMTS{sequence(p)}={MMTS(p1),…,

MMTS(pM)}。

(2)在sequence(p)中随机选择两个工件号C和D，然后交换两者的位置，形成新的工件加工顺序，即sequence(p′)，如图9所示。

步骤4基于IGP的新解再调整过程。

IGP过程是一个随机局部搜索过程，可求解NP-hard问题[21]。本文将IGP与GA结合，利用IGP过程对可行方案进行搜索，改进可行解，提高算法的改进率。

(1)判别是否执行IGP操作。

将经过步骤2和步骤3操作得到的工件加工顺序组，记为sequence(q)。计算sequence(q)的适应度值，若该值大于未执行上述操作之前的适应度值，则返回筛选阶段，否则更新工件序列。

(2)基于单工件删节的加工顺序组调整。

利用随机原则，从既有工件顺序组sequence(q)中选择一个工件号H，将其从sequence(q)中去除，生成删节工件顺序组sequence(q-H)，从而得到方案MMTS{sequence(q)}={MMTS(q1),…,MMTS(H),…,MMTS(qM)}和MMTS{sequence(q-H)}={MMTS(q1),…,MMTS(qM)}。

(3)基于贪婪原则的加工序列组重建。

将提取出来的工件号机器流MMTS(H)依次置入MMTS{sequence(q-H)}中各工件位，并计算适应值，取适应值最大的置入位，从而重建加工序列组，记为MMTS{sequence(q′)}。

(4)既有方案—重建方案的选择。

计算和比较既有方案sequence(q)和重建方案sequence(q′)的适应度值，判断重建方案的适应度值是否大于既有方案，如果大于，则用重建方案替代既有方案，否则，保留既有方案。

步骤5停止条件。

如果满足停止条件，则记录最优调度方案的适应度值和目标函数值，否则，返回步骤2。

4 仿真实验

4.1 实验设计

利用MATLAB R2014a对GA&IGP进行编程，将其与传统GA和IGP进行对比。在处理器为AMD E-300，1.30 GHz，内存为2 G双核的电脑上运行。

参考文献[13]，设置种群规模为80，最大运行次数为160，最长运行时间为500。Ns的取值分两类：A和B。A类问题中Ns都固定为5；B类问题中Ns满足[1,5]之间的均匀分布。设置Pis和ts,s+1分别满足[1,20]和[1,5]之间的均匀分布。

为公平起见，以GA&IGP的运行时间为停止条件运行传统GA和IGA。实验结果利用偏差百分比PD和运行时间CPU来衡量。令LB表示已知下界，Cbest为适应度最大的值。LB和PD定义如下[13-15]：

改进率IR表示为：

式中AI∈{GA,IGP}。

4.2 最佳调度时间表的甘特图表述

以M=10，J=3，Ns=5的MTSP-FFS为例，设置Pis和ts,s+1如表1所示。

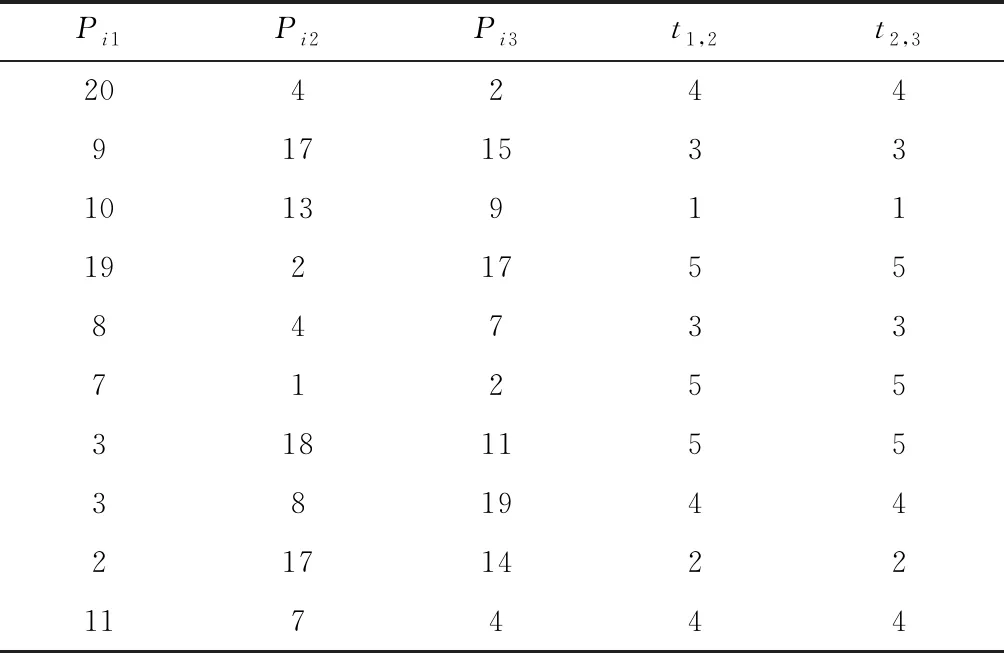
表1 加工时间与运输时间

利用GA&IGP进行求解，得到如图10的最佳调度时间表，最小完工时间为100。

4.3 不同规模问题的实验测试

为进行算法的全方位的比对分析，设计不同规模的仿真实验，实验参数生成如表2所示。

表2 MTSP-FFS的参数设置

对于每组规模随机产生10个实例，因此本实验共测试了420个实例。表3和表4分别列出了3种算法(GA&IGP、IGP和GA)的中小规模问题和大规模问题的测试结果。表中的每个值均为相同规模问题的10个实例的平均值(除最后一行)。

表3 中小规模问题的测试结果

表4 大规模问题的测试结果

续表4

4.4 测试结果分析

由表3和表4可知：

(1)从偏差百分比的结果来看，对于中小规模问题，传统GA的平均偏差百分比为12.01%，IGP为8.69%，GA&IGP为5.84%；对于大规模问题，传统GA的平均偏差百分比为24.04%，IGP为16.03%，GA&IGP为7.88%。由此可知，在相同的计算时间内，由GA&IGP得到的解的质量明显优于传统GA和IGP。随着工件规模的增大，GA&IGP的偏差百分比也有所增加，这是由于工件数的增加导致待加工工序数增多，工件之间对机器的竞争会加剧，从而使得问题求解变得更为复杂。

(2)对于所有规模的实例，在相同的计算时间331.12 s内，由GA，IGP，GA&IGP得到总平均偏差百分比分别是17.17%，11.84%，6.71%。因此，由所提出的GA&IGP得到的偏差百分比一致低于GA和IGP。随着工件规模的加大，GA&IGP的改进程度更为明显，说明所提出算法求解大规模问题时表现更佳。由表5中3种算法的相对改进率可知，GA&IGP相对GA的改进率为155.6738%，GA&IGP相对IGP的改进率为76.2766%。因此，从整体性能来看，GA&IGP的表现均优于其他两种算法。

表5 3种算法的相对改进率对比

4.5 求解质量与算法迭代次数的演进关系

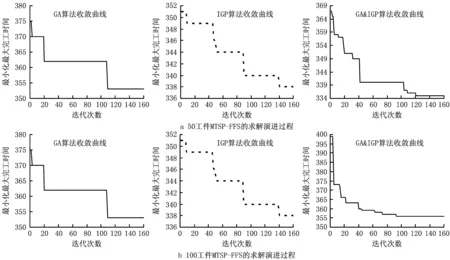
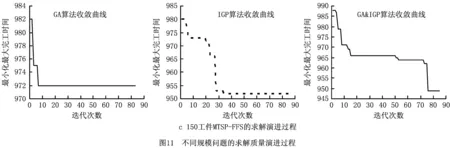
为进一步研究求解质量与算法迭代次数之间的关系，图11列出GA、IGP和GA&IGP求解不同规模问题(M={50,100,150},J=3,Ns=5)的一组实例的变化趋势图。从图11中可以看出，随着问题规模的增大，GA&IGP在较少的迭代数内得到了目标值更小的近优解，因此它的收敛速度更快。

5 结束语

本文研究了带运输时间和工件动态到达等特征的MTSP-FFS，以最小化最大完成时间为目标建立了整数规划模型。利用首要空闲机器原则，结合JAP-RSIM编码方案确定工件加工机器流系统的元胞数组，生产初始方案。进而，引入基于GA原则的交叉和变异操作对可行解进行更新操作，利用IGP的破坏和重建操作进一步调节可行解，最终完成GA&IGP融合求解策略。通过大量随机数据的实验仿真结果，说明了相对于传统GA和IGP，所提出的GA&IGP在解的质量和收敛速度方面均表现出较好的求解能力，尤其是在求解大规模问题时更具有优越性。未来研究可探讨GA&IGP融合优化策略在其他FFS问题或多目标MTSP-FFS中的应用。